Анализ энергетических процессов в электрических цепях при помощи уравнений круговых и эллиптических диаграмм

Анализ перераспределения энергии в электрической цепи – одна из наиболее актуальных и практически важных задач электротехники. В основном этот вопрос исследуется в рамках классической задачи анализа электрической цепи, т. е. при неизменных параметрах электрической цепи [1, 2]. В то же время для любой энергосистемы важным является вопрос о зависимости ее состояния от изменяющихся параметров нагрузок.

Аналитическим методом анализа изменения состояния цепи является построение круговых диаграмм токов и напряжений электрической цепи синусоидального тока при изменении одного параметра (R, L или C) [3]. Использование этих уравнений, определяющих в явном виде годографы токов и напряжений, существенно упрощает анализ динамики электрической цепи по сравнению с численным методом решения задачи. Для построения диаграмм расчеты необходимо проводить только для двух базовых режимов: режима холостого хода и режима короткого замыкания в изменяющейся нагрузке. Преимущество такого подхода особенно проявляется в случае сложных электрических цепей.

Как уже отмечалось, использование круговых диаграмм ограничивается только построением годографов токов и напряжений. Однако применение круговых диаграмм для анализа намного шире.

Если величины

K i(Y) - A + -B- и K2(Y) - A2 + -B- (1) 1 + aY 1 + aY можно при изменении параметра Y изобразить на комплексной плоскости как круговые диаграммы, то величину

K з ( Y ) -P i K i (Y ) + P 2 K 2 ( Y ) (2) также можно изобразить в виде круговой диаграммы при любых комплексных числах P 1 и P 2 . Умножая годограф тока I ^* ( Y ) на комплекс ЭДС E получаем, что комплексная мощность S ( Y )

Научно-методические вопросы

любого идеального источника также изображается круговой диаграммой

S - S_t

S ( У ) = EI (У ) = S _k + Sx^k- , 1 + '

YГ где Sx – мощность источника при обрыве в изменяющейся нагрузке У = 0, Sk - мощность источника при коротком замыкании в нагрузке У = ^ , Y Г – проводимость эквивалентного генератора относительно нагрузки Y . Также свойство (2) позволяет получить круговую диаграмму для комплексной мощности всех источников цепи

S = I S k ^.

k

Комплексная мощность нагрузки

мощности потерь Рпот (У) =IR„I2(у). Получив-n шийся в результате вектор

Р пн ( У ) + 7'Р пот ( У )                            (5)

будет характеризовать энергоэффективность системы в целом и согласно проведенным доказательствам является эллиптической диаграммой параметра Y . Если по мнимой оси откладывать потери энергии W_акт ( У ) = T I R _k r 2 за период колебаний k

T , а по действительной оси – среднюю за период энергию электромагнитного поля Wполя (У) = 0, Ш-1 IXkIk , то получившийся вектор k jWакт (У) + Wполя ( У),                        (6)

S ( У ) = U ( У ) I (Y ) = U k +

U x - U k

)

* J x - 1 k I k ⁺

^У г 7

*

Y г 7

характеризуя распределение энергии в системе, также является эллиптической диаграммой параметра Y . По отношению энергии поля к потерям энергии за период колебаний можно составить общее представление о продолжительности пере-

может быть изображена на комплексной плоскости в виде эллиптической диаграммы. В выражении (4) U _x и I _x – напряжение и ток при обрыве в изменяющейся нагрузке, U _k и I _k – напряжение и

ходных процессов и перегрузках при них.

В выражениях (1)–(6) изменяющийся параметр проводимости Y нагрузки можно заменить на сопротивление Z этой нагрузки. При этом сле-

ток при коротком замыкании в нагрузке.

Перемножая годографы вида a 1 + b 1 e^{j ф} и a 2 + b 2 e ^{- j ф} , получаем уравнение эллипса в комплексной форме a ₁ a 2 + b 1 b 2 + b 1 a 2 e^{j ф} + b 2 a 1 e ^- j ^ф . Согласно свойству (2), заменяя e j * в выражениях вида a 1 + b 1 e^{j ф} и a ₂ + b ₂ e ^- j ^ф на любую величину, изменяющуюся по круговой диаграмме (например, на 1 + У / У Г ), также получаем круговую диаграмму. Следовательно, произведение таких годографов будет эллиптической диаграммой. Выполнять указанные преобразования для выражения (4) не имеет смысла, поскольку построение годографа может быть легко выполнено по выражению (4) в любом математическом пакете.

Аналогично эллиптическая диаграмма получается для любой ветви или участка цепи, получающего (отдающего) энергию в остальную цепь. Комплексная мощность замкнутой системы (электрической цепи) является круговой диаграммой, а комплексная мощность незамкнутой системы (участка цепи) – эллиптической.

Для величин, которые изображаются эллиптическими диаграммами также можно доказать свойство (2). Это позволяет формировать и изображать на комплексной плоскости энергетические характеристики электрической цепи. Например, по действительной оси будем откладывать активные мощности полезных нагрузок P пн ( Y ) = I RJ v ( У ), а по мнимой оси - активные k

дует учесть, что режимы холостого хода и короткого замыкания поменяются местами. Например, выражение (3) при изменении сопротивления Z будет иметь вид

S ( Z ) = E ^ i

= S x

S _k - S_x

1 + —

Z _Г

.

Основными элементами уравнений круговых и эллиптических диаграмм являются: ток короткого замыкания I _{( k )}, ток холостого хода I _{( x )} и со-

противление эквивалентного генератора Z _Г . В

простых цепях эти параметры можно определить по законам Ома и Кирхгофа. В сложных цепях расчет становится более трудоемким и его целесообразно формализовать с помощью метода контурных токов (МКТ), который применим к любым линейным цепям, в том числе и со взаимоиндукцией.

Проведем контур m через ветвь с изменяющимся параметром Z . В режиме короткого замыкания ветви m (Z = 0) получаем общее решение уравнений метода контурных токов Im(k) = A-11 EpAmp , где А - главный определи-p тель цепи по МКТ, Amp - алгебраические дополнения к главному определителю, Ep – контурные ЭДС для контура p . Исключив из цепи все источники и сопротивление Zm , включив в ветвь m источник E = 1, получим сопротивление генератора ZГ =А / Amm , где Amm - алгебраическое дополнение. В режиме холостого хода для ветви

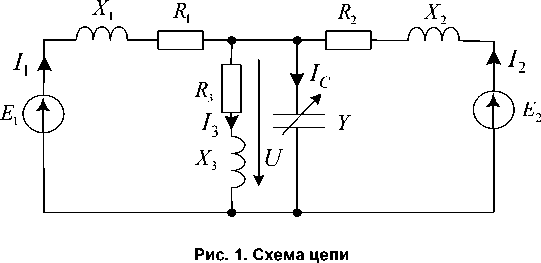
m (Z -^) контур m отсутствует, поэтому решение новой системы уравнений МКТ получается в виде Im(к) Л 1 £EpAmp , где А - главный p определитель цепи по МКТ, Лmp - алгебраические дополнения к главному определителю, Ep – контурные ЭДС для контура p . Диаграммы (3)– (6) позволяют составить представление об изменении свойств электрической цепи при изменении одного из параметров цепи. Рассмотрим применение круговых диаграмм для анализа электрической цепи на примере схемы (рис. 1). Параметры элементов цепи E1 - E2 -100 В, R1 -2 Ом, X1 -3 Ом, R2 -3 Ом, X2 -4,5 Ом, R3 - 5 Ом, X3 - 5 Ом подобраны таким образом, чтобы продемонстрировать основные свойства электрической цепи. Изменяющимся параметром будет емкостная проводимость Y конденсатора, включаемого в систему для компенсации реактивной мощности при снабжении энергией полезной нагрузки R3.

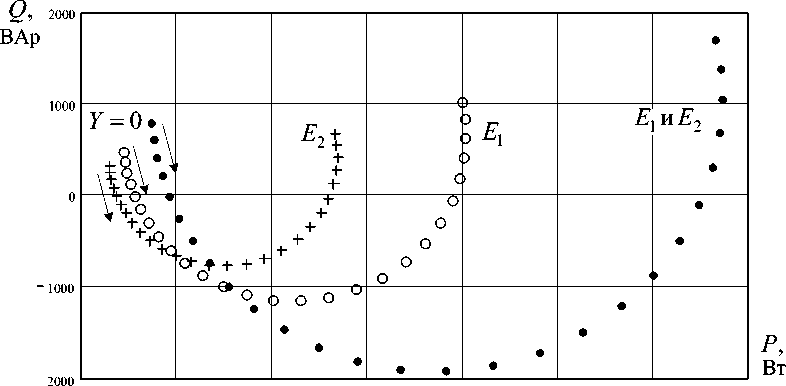
На рис. 2 построены согласно (3) круговые диаграммы комплексных мощностей каждого из источников E1 и E2, а также круговая диаграмма комплексной мощности цепи при изменении емко- стной проводимости Y . Режимы работы источников показаны «кружками» (для источника E1), «плюсами» (для источника E2) и «точками» (для цепи). Режимы построены при изменении проводимости от 0 до 0.8 Ом–1 с шагом 0.03 Ом–1, направление изменения параметра указано стрелкой. По диаграммам видно, что в цепи наблюдаются два режима (при Y - 0,12 Ом-1 и Y - 0,63 Ом-1), когда реактивная мощность источников равна нулю. Активная мощность источников значительно больше во втором режиме.

На рис. 3 построены согласно (5) векторы энергоэффективности системы в виде эллиптической диаграммы. При построении учитывалось, что элемент R ₃ является полезной нагрузкой, а резисторы R ₁ и R ₂ приводят к потерям в системе. Режимы работы цепи показаны «точками», построенными с шагом 0,03 Ом^–1, направление изменения параметра указано стрелкой. По диаграмме видно, что резонанс при Y - 0,12 Ом^-1 соответствует минимуму потерь системы P _пот =100 Вт при полезной мощности Р пн - 750 Вт. Минимум потерь достигнут за счет компенсации реактивной мощности. Резонанс при Y - 0,63 Ом^-1 достигается при больших активных мощностях источников, однако значительная ее часть теряется в резисто-

0            1000          2000          3000          4000          5000          6000          7000

Рис. 2. Диаграммы мощностей источников

Научно-методические вопросы рах R ₁ и R ₂ , а не достигает полезной нагрузки R ₃ . Это объясняется тем, что источники обмениваются энергией между собой, а не с нагрузкой R ₃ . На рис. 4 построены согласно (6) эллиптические диаграммы, характеризующие распределение энергии в системе при ш- 314 с^-1. Режимы работы цепи показаны «точками», построенными с шагом 0,03 Ом^–1, направление изменения параметра указано стрелкой. По диаграмме видно, что энергия тромагнитного поля значительно выше при Y - 0,63 Ом^-1.

Таким образом, наилучшая энергоэффективность системы достигается при Y - 0,12 Ом^-1. Далее будем считать Y - 0,12 Ом^-1 и проведем анализ цепи при изменении полной проводимости нагрузки Y _h для cos ф- 0,7. На рис. 5 показаны эллиптические диаграммы мощности для участков цепи ( S 1 - JI 1 - для ветви 1, S ₂ - JI ₂ -для ветви 2, S ₃ - U ( I ₃ + I C ) - для ветви 3 и включенного параллельно конденсатора), построенные согласно (4) при изменении проводимости нагрузки с Y _h - 0,09 Ом ¹ до Y _h - 1,5 Ом^-1 с шагом 0,03 Ом^–1. Режимы работы участков цепи показаны «кружками» (для ветви 1), «плюсами» (для ветви 2) и «точками» (для участка с нагрузкой и компенсирующей емкостью), направление изменения параметра указано стрелкой. По диаграмме видно, что изменение нагрузки позволяет достигнуть только одного резонансного режима.

Диаграмма, построенная согласно (5), позволяет провести анализ влияния различных факторов на энергоэффективность системы. На рис. 6 энергоэффективность показана при изменении фазы и действующего значения ЭДС источника E2 при E2 - 100 В (точки), при E2 - 85 В (кружки) и при E2 -100e1 j9 В (крестики). Режимы работы цепи показаны при изменении проводимости нагрузки Yн от 0 с шагом 0,03 Ом–1, направление изменения параметра указано стрелкой. По эллиптическим диаграммам видно, что изменение ЭДС одного из источников при сохранении их синфазности незначительно влияет на энергоэффективность, в то же время расхождение по фазе источников значительно ухудшает свойства системы.

Диаграммы энергоэффективности позволяют проводить факторный анализ системы, а наличие явных функциональных зависимостей получать дисперсии параметров значительно проще, чем при численных расчетах.

Приведенный пример показывает наглядность и простоту анализа свойств системы в целом и ее отдельных частей при изменении одного из параметров этой системы. Рассмотренный порядок анализа может применяться как в учебном процессе при изучении курса ТОЭ на уровне магистерских программ, так и при научных исследованиях сложных систем.

Анализ свойств системы с синусоидальными источниками можно проводить и для других функций. Например, величину

K ₄( Z ) - KZ- - A 4 + (8) K ₂ ( Z ) 1 + а ₄ Z

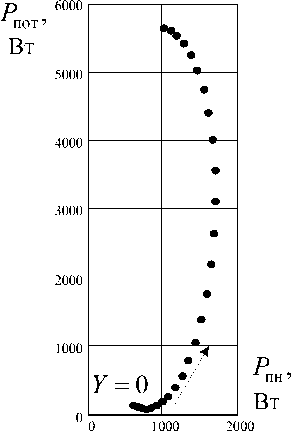
Рис. 3. Диаграмма энергоэффективности

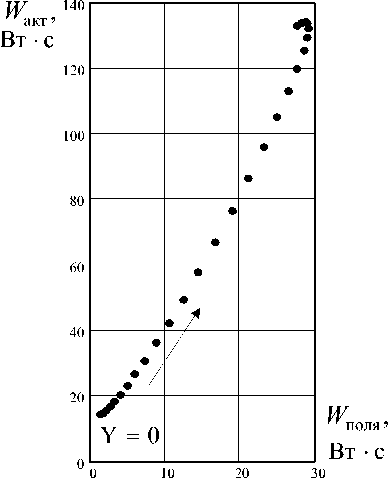
Рис. 4. Энергетическая диаграмма

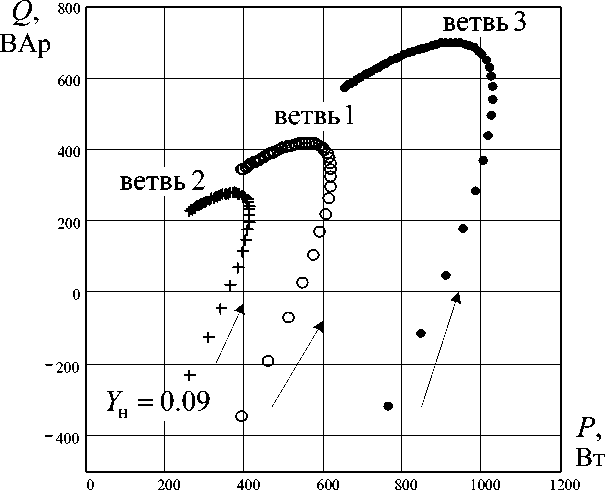
Рис. 5. Диаграммы мощности ветвей

р ;

пот,

Вт

л

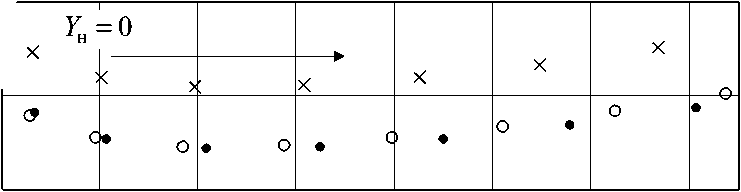
Рис. 6. Зависимость энергоэффективности от источников

р пн ,

Вт

также можно изобразить на комплексной плоскости в виде круговой диаграммы, если л   A A + в,  л          A

A ₄ = —, B ₄ = —---¹— A ₄, a₄ = a---²—

• ⁴ A 2   ⁴ A 2 + B 2   ^{4   4} A 2 + B 2

  .

  
  
  
  

Таким образом, входные сопротивления (проводимости) двухполюсников и передаточные функции четырехполюсников (по току, по напряжению и т.д.) также можно изобразить в виде круговой диаграммы при изменении параметра Z (или Y ) внутри или вне четырехполюсника. Переписывая выражение (9) для передаточной функции через режимы холостого хода и короткого замы- кания, получаем

K ( Z ) = K x +

K k - K x

,

1 + h —

Z _Г

где Kk – значение передаточной функции в режиме короткого замыкания, Kx – значение передаточной функции в режиме холостого хода, Z Г – сопротивление эквивалентного генератора относи тельно изменяющейся нагрузки, h = Ix / Ik или h = Ux I Uk в зависимости от того, что стоит в знаменателе передаточной функции: ток I или напряжение U

Параметр Z в выражениях вида (7), (10) необязательно должен быть активным R , индуктивным X _L или емкостным X _C сопротивлением ветви. В общем случае, это любая величина Z ( Z ₁ ), изменяющаяся по круговой диаграмме. Такой результат проще всего получить, если рассматривать ветвь с сопротивлением Z ( Z ₁ ) как результат преобразований в электрической цепи. Круговая диаграмма вида (7), (10) от параметра Z ₁ получается в исходной цепи. Поскольку преобразования эквивалентны, то в преобразованной цепи также получается круговая диаграмма от параметра Z ( Z ₁ ).

Некоторые элементы анализа с применением диаграмм можно распространить на случай линейных цепей с несинусоидальными источниками. Для активных мощностей полезных и не полезных нагрузок в данном случае выполняется принцип наложе-

Научно-методические вопросы ния, поэтому векторы энергоэффективности также можно изображать на комплексной плоскости. В случае несинусоидальных источников диаграммы уже не будут эллиптическими, но наглядность и простота анализа сохраняются.

Предлагаемая методика анализа основана на получении для любого сечения электрической цепи синусоидального тока в явном аналитическом виде, зависимостей токов, напряжений, мощностей, входных сопротивлений, а также передаточных функций, при изменении величины любого параметра этой цепи. Использование полученных зависимостей дает возможность в наглядной графической форме, в виде круговых или эллиптических диаграмм (годографов), представить картину процессов цепи в динамике, определить экстремальные значения токов и напряжений, условия оптимального распределения мощностей, оценить резонансные свойства цепи и экономическую эффективность того или иного режима при изменении ее параметров.