Анализ качества выбора и настройки автоматического регулятора уровня жидкости

В настоящее время в системах теплоснабжения для автоматического регулирования различных переменных технологических процессов широко используются ПИД-регуляторы и их частные варианты. Накоплен огромнейший опыт применения таких регуляторов, в частности, разработаны и апробированы различные способы их настройки. Вместе с тем, как неоднократно отмечает В .Я. Рогач в своем сравнительно недавно изданном учебнике [1], П-, ПИ- и ПИД- «...алгоритмы были получены чисто эвристическим путем» [1, с. 82 и др.] и что «...достаточно убедительное формальное доказательство целесообразности их применения... до сих пор получить не удалось» [1, с. 24].

В работах [2, 3], как нам представляется, удалось получить некоторое формальное обоснование целесообразности применения ПИД-регуляторов, здесь задача решалась методом «подгонки» передаточной функции замкнутой системы к некоторому достаточно разумному и практически достижимому виду. Найдены эталонные структуры и настройки регуляторов для типовых динамических характеристик промышленных объектов управления, при этом установлено, что все эти регуляторы принадлежат ПИД-семейству. Казалось бы, что поставленная цель достигнута, однако для полноты исследования проблемы необходимо рассмотреть вопрос о качестве переходных процессов в таких системах и о грубости этих структур и настроек, данная задача и решается в настоящей работе.

Рассмотрим объект управления с передаточной функцией вида

^об(р)=^— ехр(-тобр),              (1)

ТобР где 7"об,тоб- соответственно постоянная времени и время запаздывания объекта, р- комплексная переменная. Такими передаточными функциями описываются различные объекты регулирования уровня жидкостей в системах теплоснабжения: конденсаторы, деаэраторы, расширительные баки, выполняющие роль гидростатических стабилизаторов давления в заданных точках тепловой сети, и др.

Как известно [2, 3], близким к идеальному для такого объекта является П-регулятор с коэффици-

Т ентом передачи kD = ———, где 0 - достаточно р %б+6

малая постоянная времени. Для анализа переходных процессов в системе с объектом управления данного типа разработаны две компьютерные программы: одна для анализа переходных процессов при возмущении по заданию, а другая - при возмущении со стороны регулирующего органа. В каждой из разработанных программ предусмотрен ввод 7об, тоб и коэффициента передачи П-регулятора, каждая из программ осуществляет не только построение графика переходного процесса, но и определяет перерегулирование а и время регулирования /р , а также вычисляет значения следующих критериев:

ZK

А=ре(О|^,                      (2)

о

?к

72=fE2(0^,                        (3)

О где £(t)=x3(t)~x(t) - ошибка регулирования (рассогласование), х3(/) и x(t) - соответственно заданное и действительное значение регулируемой величины, t - время, /к - конечное время оценки переходного процесса. Здесь время регулирования /р определялось как время, по истечении которого отклонение регулируемой величины от задания не будет превышать 5 %.

В процессе численных вычислений установ-- Т лено, что во всех случаях, когда к = —— (пара метр 0 полагается равным нулю), дифференциальное уравнение замкнутой системы автоматического регулирования (САР) будет иметь вид:

хоб^7^+х(1-т:Об)=х3(1-тОб).          (4)

at

Решая уравнение (4) для единичного ступенчатого воздействия, нашли, что во всех этих случаях о=49 %. Если численное значение ^отли-

Т чается от величины -^ (0^0), то изменяется и тоб величина перерегулирования. Полученные значения показателей качества переходного процесса, например, для случая, когда Гоб = 15 с, тоб = 5 с , а кр принимает различные значения в окрестности Тоб % хода ИМ точки kD = —^ =3----------приведены в табл. 1.

тоб ед. per. вел.

Провели исследование качества переходных процессов и для других значений параметров объекта регулирования, в частности, для Т_об = 30 с, Тоб =10сидля Т^ =^15с> т_об =3с.

Анализируя полученные данные, можно отметить следующее: при эталонном (базовом) значении

Т коэффициента передачи П-регулятора к = ——

Тоб перерегулирование и в рассматриваемых САР при различных значениях Гоб,тоб получается практически одинаковым и равным ® 47 ч-49 %. Время регулирования при прочих равных условиях растет прямо пропорционально росту (Тоб + тоб) и

Т обратно пропорционально величине к_р = —^- . Ба-

Т зовая настройка П-регулятора кр = —— является тоб достаточно грубой (робастной), поскольку суще-Т ствует заметная окрестность точки к = —^, в %б которой сохраняются приемлемое качество и запас устойчивости системы (заметим, что о запасе устойчивости можно судить непосредственно по семейству кривых переходного процесса, полученных при различных настройках регулятора). Настройки П-регулятора, оптимальные по критериям (2) и (3) не совпадают как между собой, так и каждая с базовой настройкой. Так, например, в случае табл. 1 базовое значение коэффициента

Т_об % хода ИМ передачи равно к =     =3-----------, вместе с тем

Р Тоб еД- Рег-вел- оптимальное по минимуму критерия 1Х значение равно

,   .   % хода ИМ кр= 1,75----------, а оптимальное по минимуму р        ед. per. вел.

_               7 о С % Х°Да ИМ критерия 12 значение равно kD = 2,5-----------.

ед. per. вел.

Причем настройки, найденные из условия минимума критерия /2 заметно ближе к базовой настройке, в некоторых случаях их различие можно считать достаточно малым. Очевидно, что все это объясняется как существом рассматриваемого метода синтеза САР, так и определенной погрешностью выкладок при его реализации.

Показатели качества переходных процессов в САР при возмущении по нагрузке (со стороны регулирующего органа), например, для случая табл. 1 приведены в табл. 2.

В целом, анализ полученных результатов показал, что величина перерегулирования и при

Таблица 1

Показатели качества переходных процессов для Тоб = 15 с, тоб = 5 с при возмущении по заданию

, % хода ИМ кр,------------ ед. per. вел.	0,5	1,0	1,5	1,75	2,0	2,5	3,0	3,5	4,0
а, %	0	0	3,43	9,30	16,3	31,79	49	64,4	80,7
/р, с	79	32,4	17	25,4	24,8	33,2	42,2	69,8	99,8
/1?(ед. per. вел.)-с	29,47	14,99	10,71	10,32	10,40	11,47	13,79	18,16	26,99
/2,(ед.per.вел.)2 с	88,34	52,30	41,67	39,27	37,97	37,88	41,09	49,38	70,36

Таблица 2

Показатели качества переходных процессов для Тоб = 15 с, тоб = 5 с при возмущении по нагрузке

, % хода ИМ ед. per. вел. 0,5 1,0 1,5 1,75 2,0 2,5 3,0 3,5 4,0 Q, % 0 0 3,43 9,30 16,3 31,79 47,9 64,4 80,7 ?р,С 17,6 13,6 12,4 12,0 11,8 11,4 11,2 11,0 19,8 /15(ед. per. вел.)-с 0,391 0,199 0,143 0,137 0,138 0,153 0,184 0,241 0,354 /2102, (ед. per. вел.)2 • с 1,570 0,929 0,741 0,698 0,675 0,673 0,731 0,877 1,248 одинаковых настройках регулятора остается практически одной и той же как при возмущении по заданию, так и при возмущении со стороны регулирующего органа, несмотря на то, что ст в этих случаях вычисляется вообще-то по-разному [4, 5]. Кроме того, координаты точек минимума функций /1 = fx(kP) и ^2 =Л(^) ’ вычисленных для случая возмущения по нагрузке, также удивительным образом совпадают с аналогичными координатами в случае возмущения по заданию. По-видимому, данные обстоятельства подтверждают известное высказывание о том, что если САР оптимизирована для отработки возмущений по заданию, то одновременно достигается оптимум и при отработке возмущений по нагрузке [6].

Время регулирования t_P при прочих равных условиях при возмущении со стороны регулирующего органа меньше, чем в случае возмущения по заданию, что, в общем-то, достаточно объяснимо.

Если робастность рассматривать как грубость системы по отношению к изменениям параметров объекта управления, то можно привести следующие результаты. В принципе все вышеизложенное можно интерпретировать и как анализ для данного случая, здесь нужно только считать, что, якобы, регулятор настроен по параметрам объекта управления, имевшим место в недалеком прошлом, а в данный момент времени объект управления имеет те значения параметров, которые указаны в заголовках таблиц.

Если постоянная времени и время запаздывания объекта изменятся соответственно на АТоб и на Атоб, а регулятор будет иметь настройку, найденную по предыдущим значениям его параметров Т kD = —^—, то передаточная функция разомкну-Р ^+9

той системы будет иметь вид w (р\ ^ехР(~тобР) ехр(-Дтобр) (в+х^р 41+^/т^у

Используя критерий устойчивости Найквиста для систем с запаздыванием [7], нашли, что в этом случае критическая частота сокр будет равна

(О™ =---------------------- ,

• кр (e+T^xi+Ar^/r^)

поэтому условие устойчивости замкнутой системы автоматического регулирования (САР) в общем случае запишется так:

(т^+Ат^/К©*^              (5)

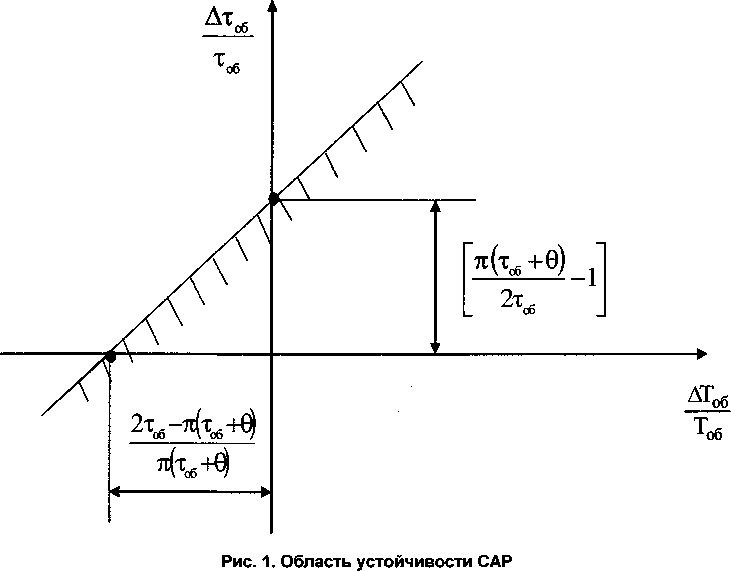
На координатной плоскости «АТ^/Т^ -Атоб/тоб» граница области устойчивости будет представляться следующей прямой (см. рисунок):

А^об _ ^(^ТОб + ®) , Q Л^Об ) _ 1             (^

об тоб        ^об

На рисунке область устойчивости - это область, расположенная правее своей границы (штриховка направлена внутрь области). Причем, нетрудно заметить, что с увеличением параметра О область устойчивости замкнутой САР расширя-

, 71 ' (Тоб +6) 1 X ется, т. к. (----—--1) - точка пересечения

2^об прямой (3) с осью ординат « Атоб /тоб» с увеличе-

-.                     z ^ ^об ^об лО _ нием 0 «ползет» вверх, а ( ——----—----) - точ-

V л-(тоб+0)  7

ка пересечения прямой (6) с осью абсцисс «АТоб/Тоб» перемещается влево. При 0=0 область устойчивости будет иметь наименьший размер, однако при этом начало координат будет располагаться все-таки правее ее границы. Следовательно, при 0=0 САР имеет некоторый запас устойчивости относительно вариаций параметров Атоб и А7об, с увеличением 0 робастность устойчивости [8] повышается.

Передаточная функция замкнутой системы по задающему воздействию будет равна

₍ х ₌_________ ехрНтоб+ДТобМ _________

Ф+Ъ XI+^ /7^+ехрНТоб +Дт_об)^] ‘ Отсюда следует, что дифференциальное уравнение САР будет иметь вид:

(в+т^ XI+АТ^ /т^^+хО-т^ -Дт_о6)= at

= U(t-x_o6-Ax_o6),                     (7)

где х - выходная (регулируемая) величина объекта, U - заданное значение регулируемой величины. Из (5) и из решения дифференциального уравнения (7) следует, что при АГоб > 0 влияние этого параметра на устойчивость (робастность устойчивости) и качество (робастность качества) САР аналогично влиянию параметра 6 [2, 3], т. е. колебательность переходной функции уменьшается с ростом АТоб, переходный процесс все в большей степени приобретает апериодический характер.

Для примера в табл. 3 приведены показатели качества переходных процессов в САР для случая, когда

^>б =15с, т^ =5с,

7^ _₃ % хода ИМ ед. per. вел. ’

Атоб=0,

а АТ^ принимает различные как положительные, так и отрицательные значения.

Аналогичные результаты получаются и при Ат_об<0, т. е. с увеличением | Ат_об | демпфирован-ность системы растет. Если же Ат_об >0, то с увеличением Ат_об перерегулирование возрастает, ухудшаются как качество переходного процесса, так и запас устойчивости системы. В табл. 4 приведены показатели качества переходных процессов в САР для случая, когда Т_об = 15 с, т_об = 5 с , 1         о % ^х°Д^а им . _   _    .

£ -_оо_=3----------? д7об =о? а Атоб прини- тоб ед. per. вел.

мает различные как положительные, так и отрицательные значения.

Выполненные расчеты показали, что если параметры объекта управления определены точно, то при 9=0 с перерегулирование в данной САР будет равно а=49 % . Если же время запаздывания

Таблица 3

Показатели качества переходных процессов для Гоб = 15 с, тоб = 5 с при возмущении по заданию при различных значениях ДТоб

А^об’ с	+1	+3	+5	-1	-3	-5
о, %	41,89	31,79	23,89	55,02	72,49	97,04
Zp , с	42	33,2	32,2	51,6	88,6	157

Таблица 4

Показатели качества переходных процессов для Тоб = 15 с, тоб = 5 с при возмущении по заданию при различных значениях Атоб

Атоб,с +1 +2 +3 -1 -2 -3 п,% 67,99 87,99 расходящийся переходный процесс 28,22 9,98 0,0005 Zp , с 85 195,6 расходящийся переходный процесс 26,4 15 9,8 модели объекта управления тоб (эта величина используется при вычислении настройки регулятора Т kD = —^— ) меньше времени запаздывания, имею-Р ^+6

щего место на реальном объекте (тоб+Атоб), то перерегулирование возрастает. Так, например, если тоб =4 с, а Атоб =1 с, то о=72 %. САР в такой ситуации, когда из-за погрешности параметрической идентификации получилось, что тоб < (тоб +Атоб), может и потерять устойчивость. В самом деле, если структура математической модели объекта и все ее параметры, кроме времени запаздывания, определены достаточно точно, то передаточная функция разомкнутой системы получается равной

• ⁼ ^^........^t—9^ ₅ поэтому САР будет

• ^Р          (6+т_об)^

устойчива лишь при удовлетворении следующего неравенства: (тоб + Атоб ) / (0+тоб ) < тг / 2 . В случае табл. 4, при Атоб=3с получили расходящийся переходный процесс, т. е. система потеряла устойчивость, что и следовало ожидать, т. к.

(тоб +Атоб)/(0+тоб ) = (5 + 3)/5> л/2 .

При отработке единичного ступенчатого задания (/(0= КО при ^->°° ^->1, т. е. САР астатическая по задающему воздействию. Передаточная функция системы по каналу «возмущение со стороны регулирующего органа - ошибка регулирования»

• ³⁰ (е+ТобХ^об+А^об^+^обехрНт^^

поэтому Um^jP0^) =-^-^ при р^О, следова-^об тельно, по данному каналу САР статическая, причем ошибка регулирования тем меньше, чем больше

Т коэффициент передачи П-регулятора kD = —— .

р т+0

Выводы. Проведенный анализ показал, что рассматриваемый метод синтеза, позволяющий од нозначно выбрать как структуру, так и параметры настройки регулятора уровня жидкостей, обеспечивает приемлемое качество переходных процессов и достаточный запас устойчивости системы при довольно заметных по размерам вариациях параметров объекта управления и погрешностях задания настроек регулятора. Поэтому данный метод синтеза можно достаточно уверенно рекомендовать для практического использования.