Анализ калибровочной зависимости волоконно-оптического датчика

Davydov Andrey, candidate of technical Sciences, associate Professor, Perm national research Polytechnic University, Russia, Perm

Pukhareva Daria, bachelor ,

Perm national research Polytechnic University, Russia, Perm

A_N_A__L_Y__S_I_S__O_F_ THE CALIBRATION DEPENDENCE OF THE FIBER OPTIC SENSOR

Annotation. The study of the calibration dependence of the fiber-optic temperature sensor based on Bragg gratings, as well as the simulation of the calibration dependence using different types of approximating functions.

Keyword. Fiber-optic sensors, approximation of experimental data, calibration function, methods of simulation of calibration function.

Датчики на основе волоконных брэгговских решеток считаются наиболее перспективными из множества использующихся на практике технологий контроля и измерений физических характеристик [2]. Волоконная брэгговская решетка – дифракционная решетка, сосредоточенная в сердцевине оптического волокна, образованная за счет периодического изменения показателя преломления кварцевого стекла под воздействием электромагнитного излучения. При прохождении излучения сквозь такое оптическое волокно происходит его частичное или полное отражение в конкретном спектральном диапазоне, коррелирующим с величиной внешнего воздействия, например, с температурой или деформацией.

Вместе с тем, для волоконно- оптических датчиков актуальна проблема повышения точности измерения физических величин, в первую очередь за счет снижения систематических погрешностей, а именно, методических и инструментальных. Методические погрешности появляются из-за несовершенства способа измерения, применения упрощающих предположений, неверно подобранного метода аппроксимации применяемых формул. Инструментальные погрешности зависят от погрешностей используемых средств измерения: неточности градуировки, конструктивных несовершенств, изменения характеристик в ходе эксплуатации. Оба этих типа погрешностей связаны с проблемой калибровки датчиков. Целью калибровки является приближение физической зависимости между входной и выходной величинами датчика некоторой функциональной зависимостью.

При калибровке датчик температуры помещается в термокамеру, температура в которой измеряется термопарой. При изменении температуры регистрируется значение длины отраженной волны (рис.1). Измеренная физическая зависимость длины волны от температуры аппроксимируется функциональной зависимостью, которая называется калибровочной функцией.

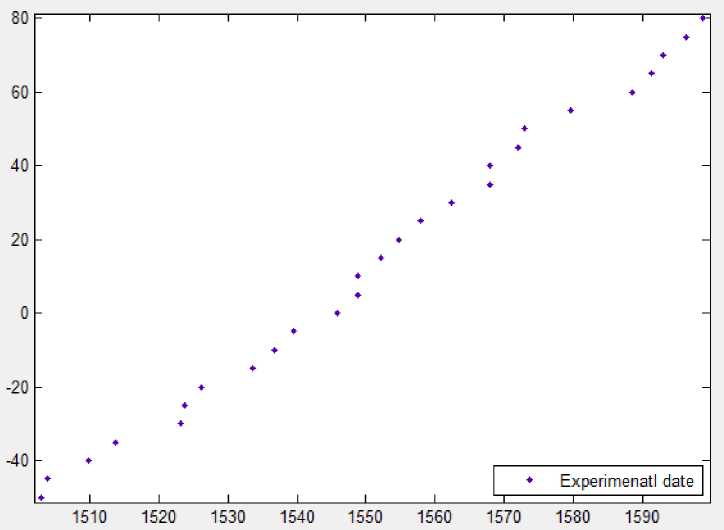
Рис. 1 – Зависимость температуры от длины волны (в условных единицах). Для анализа точности калибровочных функций рассмотрим следующие виды аппроксимирующих моделей: полиномиальные модели:

f(%) ^I-^oPt^1;(1)

экспоненциальные модели:

fM^i^e1-1*;(2)

отрезки ряда Фурье:

f (%) = a0 + 2F=i[at sin(wx) + bt cos(wx)];(3)

сумма синусов:

f(x) = Z?=i L sin(btx + ct);

степенные модели:

f(x) = CLX^b + C.

После приближения экспериментальных данных одной из функций оценка точности приближения может быть проведена как графически, так и с использованием различных критериев пригодности приближения.

Критерий SSE (Sum of squares due to error) - сумма квадратов ошибок:

^-y^'k-S'k)1

где wk –  весовые  коэффициенты, yk –  экспериментальные данные, k - значения параметрической модели.

Критерий R-квадрат (R-square) :

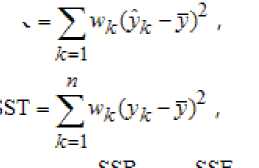
где  - среднее значение наблюдений.

Если число параметров модели m сравнимо с числом наблюдений n , то используется критерий уточненный R-квадрат (Adjusted R-square) :

1 SSE(n-l)

Adjusted R - square = 1--:—

SST(n-?n)

Стандартное отклонение ошибки RSME (Root mean Squared Error):

RSME =

SSE

n-m

С помощью математического пакета Curve Fitting Toolbox для программы MATLAB [1] по экспериментальным данным (рис. 1) определим вид функциональной зависимости, ее коэффициенты и рассчитаем критерии пригодности функциональной зависимости.

В результате установлено, что среди 22 рассмотренных функций, наиболее точно аппроксимирующих исходные данные, наилучшей по всем четырем рассматриваемым критериям является функциональная зависимость:

f(x) = a0 + ^5=1[cij sin(wx) + b cos(wx)] (10)

В табл. 1 данная зависимость сравнивается с полиномом четвертой степени, который часто используется на практике в качестве калибровочной функции датчиков температуры.

Таблица 1. Значения критериев пригодности двух калибровочных функций.

f(x)	R-square	Adjusted R-square	SSE	RMSE
12,15 - 5,47 cos(0,051x) - - 51,97 sin(0,051x) - - 5,648 cos(2 • 0,051x) - - 18,83 sin(2 • 0,051x - - 4,404 cos(3 • 0,051x)- - 11,34 sin(3 • 0,051x) - - 4,044 cos(4 • 0,051x) - - 5,367 sin(4 • 0,051x) - - 3,561 cos(5 • 0,051x)- -2,555 sin(5 • 0,051x)	0,998	0,997	76,79	2,263
6,621 •10-8x4 - 0,0005x3 + + 1,431x 2 - 1726x + + 7,637 • 105	0,995	0,993	188,584	2,928

Видно, что полином четвертой степени по всем критериям уступает зависимости (10). Таким образом, в качестве калибровочной функции данного датчика температуры лучше использовать отрезки ряда Фурье.