Анализ колебаний конструкции спутника при наведении на солнце и землю с широтно-импульсной модуляцией управления двигателями

Колебания конструкции крупногабаритных космических аппаратов (КА) могут оказывать существенное влияние на их пространственное движение в режимах начальной ориентации на Солнце и Землю (РНОС и РНОЗ), которые выполняются последовательно после завершения режима начального успокоения [1]. Широтно-импульсная модуляция (ШИМ) управления реактивными двигателями (РД) в этих режимах имеет известные преимущества (например, в отношении затрат топлива) и применяется на многих КА. Спутник связи SESAT (Siberia Europe SATellite) с крупногабаритными панелями солнечных батарей (СБ) (рис. 1, [2]) разработан НПО ПМ им. акад. М.Ф. Решетнева, выведен на геостационарную орбиту в апреле 2000 г. и успешно решает целевые задачи. При полете этого спутника была экспериментально установлена квазимонотонная амплитудная зависимость декремента колебаний панелей СБ. Поэтому проблема нелинейного анализа динамики конструкции КА данного класса с малым декрементом колебаний панелей СБ в режимах начальной ориентации на Солнце и Землю является актуальной.

Системы координат

Инерциальные системы координат (СК), используемые для описания движения центра масс (ЦМ) и углового движения КА:

I⊕ (O⊕XeIYeIZeI) – инерциальная геоцентрическая экваториальная СК (ИСК) с началом в центре Земли O⊕ , осью XeI , направленной в точку весеннего равноденствия ϒ , и осью ZeI , направленной на Северный полюс мира PN по оси суточного вращения Земли, рис. 1;

I _S (O_sX_s^IY_s^IZ_s^I) – инерциальная солнечноэклиптическая СК с началом в центре Солнца O _s , осью X^I_s также направленной в точк у ϒ и осями Y_s^I и Z ^I_s , которые получаются поворотом соответствующих осей Y_e^I и Z_e^I на угол ε_e относительно оси X_e^I ( X^I_s) , причем угол ε_e между плоскостями Земного экватора X_e^I O _⊕ Y_e^I и эклиптики X^I_s O_sY_s^I равен 0, 41015234 рад ( 23^o27^/ ), рис. 1.

Положение плоскости орбиты КА определяется долготой восходящего узла Ω _o и наклонением i _o , положение ЦМ КА на эллиптической орбите с большой полуосью a _o и эксцентриситетом e _o – радиусом-вектором r _o( t ) и истинной аномалией ν _o( t ), отсчитываемой от перигелия орбиты π , который находится на угловом расстоянии ω_π от ее восходящего узла в направлении движении ЦМ, рис. 2. Орбита КА считается известной, Ω _o, i _o, a _o, e _o, ω_π – известные константы либо функции времени, как и момент времени прохождения ЦМ О перигея орбиты t _π . Истинная аномалия ν _o ( t ) связана с аргументом широты u _o ( t ) = ω_π + ν _ο ( t ) и точно определяется в функции времени t как решение нелинейного дифференциального уравнения

V o( t) = Цо2(1 + eо cosv o( t))2/PO2 , (1) где µo – гравитационный параметр Земли, pο = aο(1 + eο2) – фокальный параметр орбиты. Текущий радиус орбиты rο (t) определяется соотношением rο(t)= pο/(1+eοcosνο(t)).

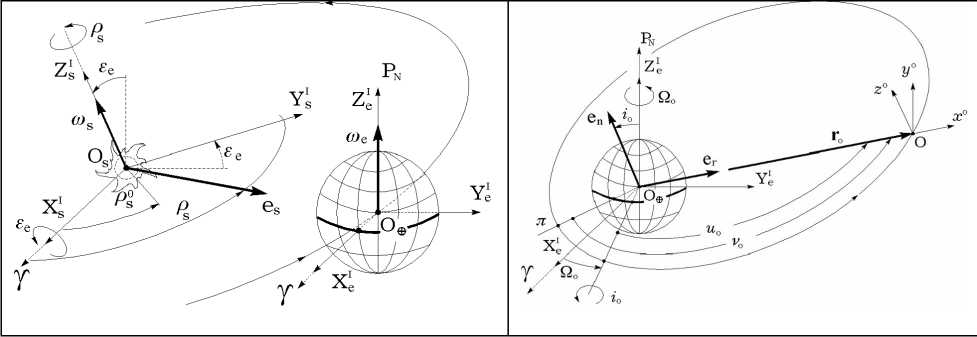
Рис. 1. Инерциальные СК

Рис. 2. Орбитальная СК

Орбитальная система координат (ОСК) O x^oy^oz^o (базис O ) вводится на рис. 2. Стандартно вводятся также связная система координат (ССК) O xyz и связанный базис B = { b i }, составленный из ортов b i , i = 1,2,3 = 1 ^ 3 = x , y , z , направленных по соответствующим осям ССК O xyz . Здесь и далее символ { • } обозначает вектор-столбец.

Кинематика и моделиортов внешних ориентиров

При традиционном обозначении [ a ] i для матрицы элементарного поворота правого ортогонального базиса относительно i -ой оси на угол a , а именно

c

a

0 - s a

[«],= 0

C a

s a

[a]2

-s

a

c a

s a 0

c

a

s a

[a]3

s

c a

ca = cosa; sa = sina.

Орт e _s (см. рис. 1), в проекциях на оси ОСК обозначаемый как e o⁽ t ) = К ⁽ t ), e o y ^(t) , e o z ^(t)} , имеет вид

e o ( t ) = T o • [ -s _eJ 1 [ -p s ( t )] з {1,0,0}, (2) где T 0 = [ u ₀( t )] ₃ [ i ₀] 1 [ Q ₀]₃ - матрица направляющих косинусов координатного перехода из базиса I _e (нижний индекс) в базис O (верхний индекс матрицы); астрономическая долгота Солнца p _s ( t ) = p 0 + ю _s ( t - t 0 ), p 0 =p _s ( t o ) , см. рис. 2, t ₀ – некоторый начальный момент

времени, ю _s - средняя угловая скорость годового обращения Земли вокруг Солнца, ю _s = 7,2921158 • 10 ^{- 5} c ^{- 1}.

При последовательности { v } 1 ^ { 0 }_з ^ { ф }₂ углов поворота рыскания V , крена ф и тангажа 0 ССК относительно ОСК матрица направляющих косинусов T ^b_o координатного перехода от базиса O к базису B вычисляется по формуле

Р», }] =[t, .t 2,t3 ] = MWvl, (3) где [•] - обозначение строки, здесь с компонентами в виде векторов-столбцов tj = {tij}. Наряду с кинематическими параметрами ориентации ССК относительно ОСК в виде углов Эйлера-Крылова у, ф, 0 и матрицы направляющих косинусов Tbo , имеющих очевидный геометрический смысл, в дальнейших расчетах используется нормированный кватернион Л0 = (X0o,X0), с векторной частью X0 = (Х0, i = 1,2,3), также однозначно определяющий ориентацию базиса B относительно базиса O . Вектор абсолютной угловой скорости ОСК V/0 относительно инерциальной СК Ie в проекциях на оси базиса O имеет представление V 0 = {0,0,v o}, причем на круговой орбите V 0 = ®0 = {О,О,ю0}. При векторе абсолютной угловой скорости ССК ω , определенном в базисе B в виде вектора-столбца ® = {юx, юy, юz}, решение кинематического уравнения с символом (о) кватернионного умножения уЛ0 = |(Л0 о ю - V0° Л0) (4) для кватерниона Л0 определяет ориентацию базиса B относительно ОСК O без какого-либо вырождения, в отличии от кинематичес-

ких соотношений для углов Эйлера-Крылова в используемой последовательности поворотов

V = ( _ro z sin ф +_ro x cos ф—v 0 sin V sin 9)/ cos 9;

ф = roy + ((гоz sin ф + гоx cos ф)sin ф—v 0 sinv)/cos9; (5) 9 = ro z cos ф —ro x sin ф — v 0 cos v , и при 4 (минимально-избыточном числе)

скалярных кинематических параметрах, свя- занных единственным условием нормировки, в отличии от 9 элементов матрицы направляющих косинусов Tob с шестью условиями ортогональности. Элементы матрица Tob выражаются по известным явным соотношениям через компоненты кватерниона

Лo, которые вычисляются в явном виде по значениям углов Эйлера-Крылова у, ф, 9 в указанной выше последовательности как Х°0 = c1c2c3+s1s2s3;

X ° = s 1 c ₃ c ₂

—

c ₁ s ₃ s ₂;

Х°2 = c1c3s2—s1s3s2; X°= c1s3c2 + s1c3s2, где ci = cos(ai/2); si = sin(ai/2); a1 =v ; a2 =9 ; a3 = ф. Это позволяет легко опреде- лить начальные условия для интегрирования кватернионного кинематического уравнения

• (4)    с соблюдением условий нормировки и

• однозначно определить текущую ориентацию ССК относительно ОСК. Решение кинематического уравнения Л = 1Л ° ю для кватерниона Л определяет ориентацию базиса B относительно инерциального базиса Iф также без каких-либо сингулярностей. Направления ортов e° и eo в проекциях на оси ССК вычисляются по соотношению eo = Tob {1,0,0} = t1 = {t11, t12 ,t13}. При этом орт направления S из ЦМ КА на Солнце определяется как S = — es, а орт направления E на центр Земли - как E = — er, рис. 2.

Моделирование движения деформируемой конструкции КА

Для получения приближенных моделей движения упругих КА используется метод конечных элементов, представляющий собой локализованный метод предполагаемых форм колебаний. Применяемый здесь подход заключается в представлении упругих колебаний элементов конструкции КА в виде конечного числа тонов. При этом вычисляются матрицы коэффициентов взаимовлияния движений всех подконструкций КА как абсолютно твердых тел, включая корпус КА, так и деформируемых тел. Собственные формы и парциальные частоты колебаний каждой панели СБ КА Sesat рассчитаны с учетом nq = 10 низших тонов в стандартной нормировке, значения парциальных частот колебаний панелей представлены в [1,2]

Модель динамики углового движения КА с упругими неподвижными панелями СБ, составленная при упрощающих предположениях [2], имеет вид

A ^o

ю

• • q

F ^ro

F ^q

F

F ^q

— H — ю X G + M do + M _o

— Dq — Wq

A ^o

J ( Y )    D q

( D ^q)^т I q 2 n

Здесь q = {q1, q2} - вектор обобщенных координат упругих колебаний панелей СБ, где qkcR nq , k=1, 2 – вектор обобщенных координат упругих колебаний k-й панели СБ; f q = {Fq, fq} – вектор-столбец обобщенных сил, соответствующих колебаниям панелей СБ, где Fq = —(5/п)Qk qk—Q2qk ; диагональная матрица Qk = diag{Qks} составлена из парциальных частот Qks, s = 1 ^ nq и 5 - логарифмический декремент колебаний панелей СБ, матрица собственного демпфирования D = (5 /п) Q, причем матрицы Q = diag{ Q 1, Q 2} , W= Q2; G = J(y)ю + H+ Dq(y) q - вектор кинетического момента (КМ) упругого КА с гироскопическим стабилизатором (ГС), где H – вектор собственного кинетического момента ГС, причем вектор H = 0 в режимах наведении КА на Солнце и Землю; Mо = M! + Mo - суммарный вектор возмущающих моментов относительно полюса О, где Mgo– вектор гравитационного момента и Mso – вектор момента возмущающих сил солнечного давления, остальные внешние возмущающие моменты на геостационарной орбите пренебрежимо малы; Mdoo– вектор моментов двигательной установки ориентации (ДУО). Прямоугольная матрица Dq (у) инерционного взаимовлияния движений панелей СБ и корпуса КА представляется матрицей-строкой Dq = Dq(y) = [Dq(y), Dq(y)], при- чем структура матриц D1q и Dq2 инерционного влияния упругих панелей СБ такова:

• -    матрица D q = { D q 1 , D q2 , D q3 } представляется столбцом, составленным из строк,

• -    D kj - строки матриц влияния, j = 1,2,3 - номер строки; k = 1,2 - номер панели.

Тензор инерции КА J в полюсе O при произвольном положении панелей СБ, определяемом углом у , вычисляется по формуле J = J ( y ) = J o + 2 J ^p( y ), причем тензор инерции J ^p( y ) каждой панели СБ рассчитывается по соотношениям

J ^p( y ) =

J X C Y + J^P y S 2 J Xd C Y S Y 0

pd

J _xy C _Y S _Y

J X S 2 + J^P y C 2

0 J z ^p

;

J Pd = J P - J p ; C y = cos Y ; S y = sin Y , где y = 3 n /2 для положения панелей СБ при завершении режима успокоения, когда спутник вращается в ИСК с вектором угловой скорости _to ~ _to ^c, где to ^c = { to X , ra y , to Z } - вектор-столбец, составленный из командных угловых скоростей по осям ССК O xyz . Для спутника Sesat принято ra c = to Z = 0 o /с; ra y = 0.2 o /с , поиск направления на Солнце осуществляется вращением КА относительно оси O y ССК.

Модели компонентов системы ориентации

Приборный состав системы управления ориентацией КА в РНОС и РНОС состоит из ДУО на основе шести термокаталитических реактивных двигателей (РД) с широтно-импульсной модуляцией (ШИМ) тяги, приборов ориентации на Солнце (ПОС) и Землю (ПОЗ), блока трех одноосных датчиков угловой скорости (ДУС), а также БЦВМ, реализующей алгоритмы фильтрации дискретных измерений и цифрового управления.

Математические модели ДУО и блока ДУС подробно представлены в [1,2], поэтому здесь приводятся только необходимые соотношения. Модель ШИМ нормированного сигнала Pⁿ ( t, τ _k ^d ) включения РД принята в виде

'0    Tk < Tm

d	т k	т т	-	т k	< т т
т k =1	т т	m т	-	т k	< T u

T u

T k >  T u

Здесь Pn(t,тdd) e {0,1}, k e No ^ [0,1,2...) -сигнал включения реактивного двигателя, t e [tk,tk + тd), тd =тd(tk) - длительность включения; тk - командный входной сигнал, поступающий в моменты времени tk = k Tu, где Tu – период управления. Изменение нормированной тяги Pdn(t) каждого РД с учетом времен-нуго запаздывания Tzdu описывается дифференциальным уравнением TdPП iPn =Pn(t-Td , тd) с d d             zu, k начальным условием Pdn(t0) = 0, где Td- постоянная времени, причем Td = T+d, если Pn = 1; иначе Td = Td. Для последовательности командных импульсов Pn(t,Td) с длительностями тd на полуинтервалах времени t e [ tk, tk+1) начальные условия для этого уравнения в моменты времени t = tk + Tdu и t = tk + Tdu + Tk получаются “припасовыванием” по непрерывности решения Pdn(t).

Каждому j -му РД D j , j = 1 ^ 6, сопоставляется вектор текущей реактивной тяги P. ( t ) = P^mP_dⁿ j ( t ) • P j с фиксированным ортом p _j и началом в точке O^d _j , где _P^m – одинаковое для всех РД значение текущей максимальной тяги. Расположение точки O^d _j относительно полюса O определяется радиусом-вектором ρ _j . Управляющие моменты ДУО относительно осей O x , O y и O z ССК создаются парами РД (D₁,D₂) , (D₃,D₄) и (D₅ ,D₆) соответственно, причем РД с нечетным номером в i -ой паре создает управляющий момент положительного знака относительно соответствующей i -ой оси, i = x , y , z. Логика формирования команд т _jk включения каждого j -го РД в составе ДУО учитывает знак командного входного сигнала v _ik по соответствующему каналу управления i = x , y , z и для значений индекса k e N₀ описывается следующим алгоритмом:

^т ik = 1 v ik I; s ik = sign v ik ; i = x , y , z ;

pⁿ( t , т d ) =^

tk - t < tk +т d

tk +T k - t < tk+1

^т 1 k

1^т 1 k

= ^т xk , ^т 2 k = ⁰ , = ⁰ , ^т 2 k = ^т xk ,

s xk >  0;

s xk

< 0;

<

^T 3 k = ^T yk , ^T 4 k = 0,

^T 3k = ⁰ , ^T 4k = ^T yk ,

^T 5 k = ^T zk , ^T 6 k = 0,

T5k = 0, T6k = Tzk , syk > 0;

s yk <  0;

s zk >  0;

s zk <  0.

Вектор управляющего момента M ^d _ο ^ο , формируемого ДУО относительно полюса О, в проекциях на оси ССК вычисляется по формуле 6

j =1

Используются обозначения M _i ^m для максимальных значений модулей моментов ДУО по каналам управления и стандартные функции:

• ограничения

Sat( a , x )

x

a sign x

|x| <  a

|x| >  a ^;

Sats( a, k, x ) =

k x

a sign x

x | <  a /k x | >  a /k ^;

• релейная гистерезисная функция общего вида

Relh( a ,b, X , x( t ))

signx( t )

x > X b x <  b

Relh( a ,b, X ,x( t ₀)) = a е { - 1,0,1}

• •    функция “генерации” импульсов длительностью т <  T u , начиная с момента t_k :

  Puls( t _k, T ,x_k) = <

  
  

  x_k 0

  
  

t k < t < t k + т tk+ т < t < tk+1

• •    функция фиксации сигнала на периоде T u : ^Zh ( ^Tu^,xk ) = ^Puls( t k ^,Tu^,xk );

• •    функция квантования по уровню y = Qntr( a , x ) = a E[( x / a ) + 0,5sign x ], где a -шаг дискретизации и E [ • ] - символ целой части числа [ • ].

Применяются также стандартные обозначения для значений скалярного дискретного сигнала y( t_k ) = y _k и y( t s ) = y _s соответственно в моменты времени t_k = k T_u и в кратные им моменты времени t s = s T q с периодом измерения T q , причем кратность n q = T_u / T q – целое положительное число, где целые числа k,s е N₀.

Модель блока измерителей скорости (БИС) корпуса КА to ( t ) = { ro _x( t ), ro _y( t ), ro z ( t )} представляет совокупность трех однотипных каналов измерения угловой скорости ro i ( t ), i = x,y,z одноосными ДУС, каждый из них описывается соотношениями

T“( b ^s( t ) + ro ^s( t ) = ro ( t );

ro se ( t ) = Sats(b “ , k ^ш , ro ^s ( t ) + ro ^b);

ro " = ro ^se( t _s) + ro _sⁿ; ro d = Qntr(d “ , ro " ), где T_q – период квантования измеряемого сигнала по времени, ω _s^d – дискретный выходной сигнал и все параметры описаны в [2].

Выходными сигналами оптико-электронного ПОС являются признак наличия Солнца N^s в его поле зрения и сферические угловые координаты 0 _s , v _s орта S направления на Солнце относительно орта b ₁ (оси O x ) ССК. Рабочее поле зрения ПОС составляет 2 A S = 184 ° в плоскости B^sOC^s и 2 B_S = 64 ° в плоскости A^sOB^s - см. рис. 3, г де представлена привязка приборных осей ПОС к осям ССК и связь углов a _s и р _s, определяющих положение орта S в приборной СК, с углами 0 _s, v _s.

В моменты времени t s = t_s - T_z^s по значениям проекций орта S ( t ) = { s_x ( t ), s_y ( t ), s_z ( t )} в базисе B вычисляются угловые координаты a _s , в _s этого вектора в приборной СК, признак наличия Солнца N^s в поле зрения ПОС, и далее в дискретные моменты времени t _s = s T q формируются дискретные значения измеренных углов 0 d s , v d s с учетом методических погрешностей, дискретного шума измерения и дискретизации сигналов по уровню:

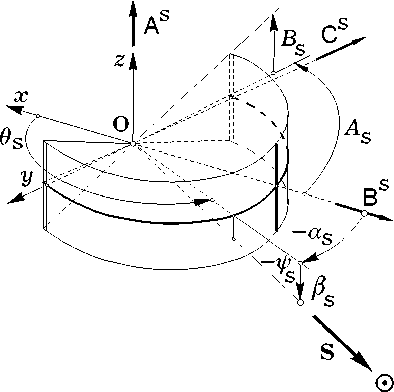
Рис. 3. Схема ПОС

β _s ( t_s ′ ) = arcsin( s_z ( t_s ′ ));

α _s ( t_s ′ ) =π- arctg( s_y ( t_s ′ )/ s_x ( t_s ′ ));

N ^s s = N ^s ( t s ′ ) = n α ( t s ′ ) n β ( t s ′ );

ss

ψ ^s ss =ψ ^s ss ( t s ) =β s ( t s ′ )N ^s s ;

θ ^s ss =θ ^s ss ( t s ) = ( π-α s ( t s ′ ))N ^s s ;

x_s^d = Qntr( d^x , x_s^s + x^b + x_sⁿ ), x = ψ _s ,θ _s .

Здесь n_x ( t ) = Nh( n_{x 0}, b_x , λ _x , x ( t )), x = α _s , β _s , релейная гистерезисная характеристика наличия ориентира

Nh( a , b , λ , x ) = 1 - Relh( a , b , λ ,| x |) графически представлена на рис. 4; ψ ^b _s ,θ ^b _s – квазипостоянные погрешности ПОС, обусловленные неточностью привязки приборной СК к ССК; ψ ⁿ _ss , θ _s ⁿ _s – дискретные шумы измерения, которые считаются гауссовскими независимыми стохастическими процессами с нулевым математическим ожиданием и среднеквадратическим отклонением _σ ^s ; d ^{θ s} ₌ d ^{ψ s} ₌ d^s – шаг квантования выходных сигналов по уровню.

Прибор ориентации на Землю (ПОЗ) предназначен для определения отклонения оси минус O x ССК по углам тангажа и крена от направления на центр Земли. Принятая математическая модель описывает формирование выходных дискретных сигналов ПОЗ θ ^d _s , ϕ ^d _s об углах отклонения КА по тангажу и крену и признак наличия Земли N^e в поле зрения прибора.

Схема привязки приборной СК ПОЗ к ССК представлена на рис. 5. В моменты времени t ′ _s = t_s -T_z^e по значениям проекций орт а E ( t ) = { e_x ( t ), e_y ( t ), e_z ( t )} в базисе _B вычисляются угловые координаты α _e , β _e этого вектора в приборной СК, признак наличия Земли N^e в поле зрения ПОЗ, и в моменты времени t _s = s T_q формируются значения измеренных углов θ ^d _s , ϕ ^d _s с учетом методических погрешностей, дискретного шума измерения, ограничения и дискретизации сигна-

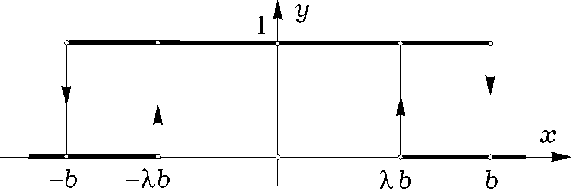
Рис. 4. Характеристика наличия ориентира

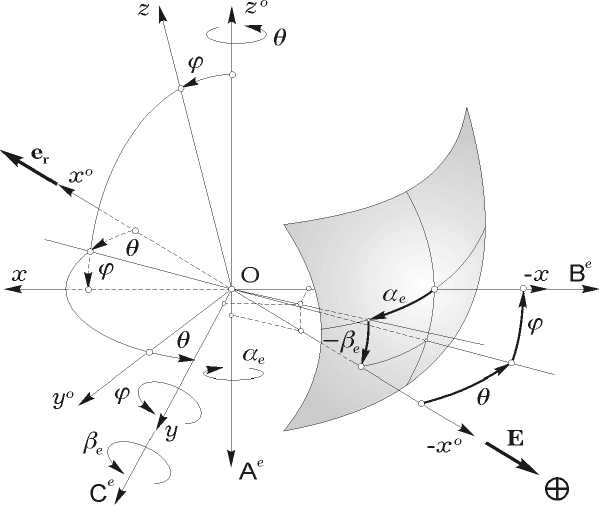
Рис. 5. Схема ПОЗ лов по уровню:

β _e ( t_e ′ ) = arcsin( - e_z ( t_s ′ ));

α _e ( t_e ′ ) = arctg( e_y ( t_s ′ )/ e_x ( t_s ′ ));

N s ^e = N^e( t s ′ ) = n α ( t s ′ ) n β ( t s ′ );

ss nx(t) = Nh(nx0, bx, λx, x(t)), x= αe,βe

ϕ s ^s =ϕ ^s s (t s ) =-β e (t ′ s ) ⋅ N ^e s ;

θ ^s s =θ ^s s (t s ) =α e (t ′ s ) ⋅ N s ^e;

x_s^d = Qntr(d ^x ,Sat( a^x , x_s^s + x^b + x_sⁿ )), x =ϕ,θ .

Здесь ϕ ^b ,θ ^b – квазипостоянные погрешности ПОС, обусловленные как неточностью привязки приборной СК к ССК, так и дрейфом точки отсчета статической характеристики из-за несферичности Земли; ϕ _s ⁿ , θ _sⁿ – дискретные шумы измерения, которые считаются гауссовскими независимыми стохастическими процессами с нулевым математическим ожиданием и среднеквадратическим отклонением _σ ^e ; a ^ϕ , a ^θ – уровни ограничения выходных сигналов; d ^θ ₌ d ^ϕ ₌ d^e – шаг квантования выходных сигналов по уровню.

Дискретные алгоритмы фильтрации и управления

Оператор осреднения с одинаковыми весами только nq последних измерений ys сигнала с получением оценки yk , оптимальной по методу наименьших квадратов, называемый обычно алгоритмом осреднения координаты (АОК), имеет описание yk =MS(ys)≡( ∑ys)/nq ;

s = k -n_q +1

n q = ^Tu / ^Tq ; ^k = ^E[ s /n q ], ^k, s ^{e N} 0 •

Для КА Sesat принято T_q = 1c и T u = 4c, поэтому здесь кратность периодов n_q = 4. АОК используется для многократной дискретной фильтрации выходных дискретных сигналов to d БИС, 0 1 , у 1 ПОС и в ! , o d is               ss ss                  s s

ПОЗ:

to k = M ^{S( to} d s ), i = ^x, y ^,z ;

0 sk = MS( 0 ds ) ; v sk = ms( v ds );        (8)

k x и k to — коэффициенты усиления, у s — постоянное командное значение угла рыскания и c ₁ – ограничение сигнала по модулю.

С целью наведения КА на Солнце по кратчайшему пути после попадания Солнца в поле зрения ПОС (т.е. при N ^s = 1) предлагается дискретный векторный алгоритм управления. Согласно этому алгоритму сначала формируется предварительный дискретный сигнал

ф k = MS( ф d ) ; 0 k = MS( 0 s ').

В РНОС на спутнике Sesat используется канальный алгоритм формирования дискретных команд v _ik включения пар РД в состав е ДУО:

по каналу тангажа vzk = kp(kpp Sat( c з, 8 sk) - k to tozk), (9) где

⁸ zk

0 s — 0 sk

k

E ^{( to} zA )

, j =0

N ^s K n = 1;

N ^s K n = 0;

N ^sto N ^s = 1;

N n ^to N ^s = 0;

^{(| v} sk < V sn ) &  ^{(| to} yk ^| < ^to yn );

^{(| v} sk >V sn ) v ^(| ю yk ^| > to yn );

k_p – коэффициент компенсации вариации тяги РД, см. [1,2], k z и k to — коэффициенты усиления, 0 s = 0 _s = 7/12 л - командное значение угла ориентации КА относительно орта S , рис. 3, v sn = 3 ° , m yn = 1 угл. мин/с и c 3 -некоторая константа;

по каналу крена v yk = kp ( kp Ф s (c 21, c 22,N s , 8 yk ) - k to toyk ), (10) где

. ( , _ATs \ [Sat( a , x ) N ^s = 1;

ф l a , b ,N ^s , x ) =]

• ^{sV 7}   - b N ^s = 0;

• ⁸ sy =ф s v sk cos ⁰ sk ; ^{kp и k} yy ^- коэффици енты усиления, ф ^с = 0 - командное значение угла крена и c ₂₁, c ₂₂ – некоторые константы;

по каналу рыскания v^ = k„(kpp Sat( c, 8 xsk) - k totoJ, (11) xk p x        1 sk x xk где

~k = -kp(kp pk + ktotok),i = x,y,z -1,2,3, (12) где при постоянном векторе bs требуемого положения орта направления на Солнце в ССК и обозначениях s(t) = sл' = x, y,z ; is is sik = MS(sis); Sk = {sik} компоненты Pk вектора pk = {p1 k, p2k, p3k} вычисляются по соотношению pk = bs x Sk. Далее вычисляется значение ~™ = max(| ~k |,i = x,y,z) и при условии ~m > Tu результирующие дискретные команды включения ДУО по каналам приводятся к масштабу максимальной длительности работы РД на такте управления по простой формуле

V» = T u ~ k /~ mm , i = x , y , z .      (13)

В РНОЗ дискретное управление vzk по каналу тангажа формируется в соответствии с алгоритмом управления (9) по этому каналу в РНОС. Одновременно ПОЗ при наличии Земли в его поле зрения (т.е. при ne = 1) выдает дискретные сигналы фs и 0ds , которые после осреднения с помощью АОК принимают в моменты времени tk значения фk, 0k (8). При выполнении условия (| фk |< 1 o) & (| 0k |< 1 o) координата 0sk в (9) заменяется на координату 0k. Алгоритм управления по каналу крена в этом режиме имеет вид vyk = kp(kp ф e (c 2,N e , 8 yk ) - k to toyk ), (14) где 8yk = фk- фk;

Ф . ( b ,N e , x ) =

x

s

N ^e = 1;

_- b  N ^e = 0;

^x sk

V s —V sk sin ⁰ sk

k

Sat( c „ E (® xk T,))

j =0

N ^s = 1;

N ^s = 0,

kp и kto - коэффициенты усиления; фk = 0 -командный сигнал по углу крена и c2 –поис-ковая уставка. Наконец, алгоритм управления по каналу рыскания в РНОЗ представляется соотношением vxk = k„(kpSat(cj,8xk)-kx’to.J, (15) xk p x        11 sk x xk где

^c 12 ^-v sk            ^N e = 0;

V c + K s v ok -^_sk N ^e = 1; s o sk sk

^K o ^s

= <

(| ф k\ < 1 ° )&(\ to x_k\ <_to 0 )

&( \ to y_k\ < _Ю 0 )&( \ to zk\ < _Ю 0 ); \ (\ ф _к\ >  i o ) л (\ ш х_к\ > _ю о )

^{л (} \ to yk | > to 0 ) ^{л (} \ to zk | >ю 0 );

kPp и к to — коэффициенты усиления; vtok = arcsin(sin(Ps(tk) sinse) - командный сигнал на отработку солнечного склонения; ps (t) - астрономическая долгота Солнца, см. рис. 1; уc - командное значение угла рыскания; параметр to0 = 1 угл. мин/с; c11, c12 – соответственно ограничение сигнала по модулю и поисковая уставка.

Динамические свойства упругого объекта

Выполняя линеаризацию пространственной упругой модели КА (6) при постоянном значении вектора H КМ ГС, совпадающего по направлению с ортом b ₃ ССК относительно некоторого состояния КА в инерциальном базисе при произвольном векторе вращения КА _to ^c, M = M do , q = q = 0 и векторе невязки 5 _Ю = _ю - _ю ^с по угловой скорости КА получаем линейную непрерывную модель.

В РНОС вектор кинетического момента ГС H = 0 и поисковое движение для захвата Солнца ПОС выполняется относительно оси Oу ССК, т.е. вектор toc = {0,toy,0}, где toy = 0,2 o/c. При практически диагональном тензоре инерции КА с панелями СБ в парковом положении движение КА по каналу крена отделяется от взаимосвязанных движений по каналам рыскания и тангажа. Отсюда следует, что влияние упругости конструкции КА по каналу крена в РНОС будет точно таким же, как и в режиме успокоения, причем частотные характеристики по каналам рыскания и тангажа будут изменяться только в их низкочастотной части за счет гироскопической взаимосвязи каналов поисковой угловой скоростью to у =0,2 %=0,0035р/с вращения спутника относительно оси крена. В режиме поиска Земли уже все три канала взаимосвязаны поисковой угловой скоростью, что четко проявляется на частотных характеристиках каналов. Также как и в РНОС, при заданном значении командной угловой скорости поиска Земли завязка каналов в РНОЗ является слабой , поэтому вполне обоснованно можно автономно проводить параметрический синтез дискретных алгоритмов управления по отдельным каналам при наведении КА как на Солнце, так и на Землю.

В режиме предварительной ориентации на Землю, который реализуется после завершения РНОЗ, выполняется разгон ротора ГС [3] до величины его КМ Н = 85 Нмс. Для анализа собственных динамических свойств упругого КА, как непрерывного объекта управления, при разгоне ротора ГС в этом режиме были построены частотные характеристики по каналам для трех фиксированных значений модуля КМ в парковом состоянии ГС. В качестве примера на рис. 6 представлена логарифмическая частотная характеристика по каналу рыскания. Здесь явно видно, что при наличии КМ ротора ГС появляется дополнительный резонансный пик, соответствующий

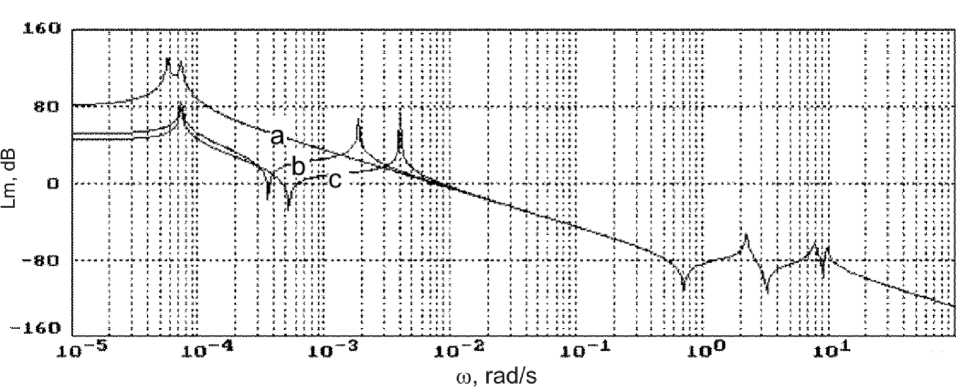
Рис. 6. Канал рыскания: a) H=0; b) H =40 Нмс; c) H =85 Нмс

нутационным колебаниям КА из-за наличия собственного кинетического ГС. Этот резонансный пик последовательно сдвигается вправо с возрастанием значения КМ H, как параметра. Тем не менее, при номинальном значении H= 85 Hмс среднечастотный участок имеет наклон 40 dB/dek, что вполне соответствует условиям автономного параметрического синтеза дискретных алгоритмов управления по отдельным каналам также и в этом режиме.