Анализ колебаний железобетонного каркаса при внезапном удалении колонны

Обзорная часть

Прогрессирующее обрушение представляет собой экстремальное событие в зданиях и сооружениях, начинающееся с локального повреждения какой-то конструкции, а затем переходящее в виде цепной реакции на другие части сооружения, приводя его либо к частичному, либо полному разрушению. К данному явлению, проявляющему непропорциональный характер разрушения, обращено внимание инженеров и научных специалистов как отечественных, так и зарубежных, о чем свидетельствуют многочисленные публикации и конференции [1–11].

Непропорциональный характер разрушения состоит в том, что отказ одного конструктивного элемента, напр., колонны или ригеля, имеющее вид локального события в конструкции, неожиданно принимает лавинообразный характер и может вызвать обрушение всего здания. Особенностью этих разрушений также является то, что они происходят, как правило, при выполнении всех норм и правил строительного проектирования. Сложный и непредсказуемый характер таких разрушений вынуждает выделить их в особую категорию так называемых запроектных воздействий [1], не подчиняющихся условиям нормальной эксплуатации строительных объектов.

Поэтому первостепенной задачей строительной науки является обеспечение живучести зданий и сооружений. Этой теме в последнее время посвящено огромное количество различных подходов к проектированию зданий и сооружений по их защите от прогрессирующего обрушения.

В России на основе этих подходов разработан ряд мероприятий по предотвращению прогрессирующего (или лавинообразного) обрушения для различных категорий зданий (высотных, монолитных жилых, крупнопанельных, большепролетных сооружений), приведенных в рекомендациях [12, 13], публикациях [2, 4, 6, 10, 14] и нормативных документах [15]. Аналогичные разработки по защите конструкций зданий и сооружений от прогрессирующего обрушения ведутся за рубежом (американские [16, 17] и европейские [18] стандарты и требования).

Из обзора публикаций зарубежных источников следует, что основные направления исследо- ваний по методам оценки живучести зданий можно условно разделить на три направления. Первое направление относится к методам разработки надёжности конструктивных элементов с использованием 2- и 3-мерных моделей разрушения [8, 10, 19–21], второе – к методам разработки мероприятий, которые связаны с повышением сопротивляемости конструктивной схемы к разрушению [7, 22–24]. Третье направление исследований связано с созданием стойких к разрушению каркасных зданий, для этого используется опыт проектирования и расчёта конструкций в условиях сейсмических воздействий [22, 24].

В большинстве случаев все исследования по оценкам сопротивления нагрузки и режиму внезапных отказов конструкции получены либо по результатам численного моделирования на основе различных модификаций метода конечного элемента [25], либо экспериментальным путем. Отсутствие аналитических методов расчета конструкций на прогрессирующее обрушение объясняется сложностью задачи, хотя при этом отмечается важность теоретических исследований по созданию аналитических моделей для анализа поврежденных конструкций [1, 2].

При внезапном выключении критического элемента (колонны или ригеля) поврежденная система из состояния покоя переходит в состояние движения. Это связано с тем, что положение статического равновесия для системы уже становится невозможным и переход в режим колебаний – это вынужденный для неё шаг, чтобы сохранить свою целостность. Поэтому при создании математической модели колебаний поврежденной системы следует учитывать наличие инерционных эффектов и сил сопротивления, свойственных задаче динамического анализа. Решение этой задачи требует построения системы уравнений динамической реакции расчетной модели с выключающимся конструктивным элементом, что при численном моделировании выполнить чрезвычайно сложно.

Однако решение такой задачи по созданию математической модели колебаний и построению комплекса уравнений динамической реакции конструктивной системы с выключающимся несущим элементом можно получить на основе временного анализа. В статье предложен подход к расчету по- врежденного каркаса с использованием метода моделирования альтернативного пути [10, 12] в рамках теории временного анализа дискретных диссипативных систем (ДДС) [26]. Анализ колебаний проведён для 2-этажного железобетонного каркаса при внезапном выключении угловой колонны.

Метод исследования

Условия динамического равновесия расчетной модели, рассматриваемой в виде ДДС, представляется системой обыкновенных дифференциальных уравнений (ОДУ) движения. В матричной форме эта система вместе с начальными условиями имеет вид:

MY( t ) + CY ( t ) + KY ( t ) = f ( t ), 1 ⁽¹⁾

• Y _o( 1 0 ) = Y(1 0 ), Y _o( t o ) = Y(t o ), J ₍2) где M = diag ( m 1 , ... , m n ), C = C ^T, K = K Т - матрицы масс, затухания и жесткости; Y ( t ), Y ( t ), Y ( t ) - векторы перемещений и их производных; f( t ) = Q + P ( t ) - вектор внешней нагрузки, содержащий векторы статических ( Q = KY_st ) и динамических P ( t ) воздействий; Y st - вектор статических перемещений расчетной модели.

В процессе колебаний помимо внешней нагрузки на узлы дискретной модели действуют внутренние силовые параметры модели - восстанавливающие, диссипативные и инерционные силы. Они представляют соответствующие векторы левой части ОДУ (1):

R ( t ) = KY ( t ), F ( t ) = C Y ( t ), I ( t ) = - MY ( t ). (3)

В случае внезапного разрушения колонны происходит снижение параметров жесткости расчетной модели (каркаса), характерное для конструктивнонелинейного процесса. Математическая формулировка этого процесса, определяемая связью между восстанавливающими силами и перемещениями узлов модели, приведена в [26] и имеет вид:

R ( t ) = K i Y ( t ),

K = K о ( t <  1 1 ), K = K i ( t >  1 1 ), (4) где t 1 - время, при котором происходит выключение (удаление) колонны.

Матрица жесткости K i ( i = 0, 1) в (4) при t <  1 1 формируется по расчетной схеме, соответствующей базовой модели (БМ), а при t >  1 1 - по схеме поврежденной модели (ПМ). Для БМ индекс i = 0 в дальнейшем опущен.

Помимо уравнения движения расчётной модели конструктивно-нелинейной системы огромное значение имеет уравнение движения собственных форм колебаний ДДС, которое является характеристическим по отношению к однородному ОДУ в (1):

MS2 + CS + K = 0, (5) где S е Мп(С). Матрица S с помощью фундаментальной матрицы Ф(t) = eSt осуществляет связь между однородным ОДУ в (1) и характеристическим уравнением (5). В матрице S заключены свойства внутренних динамических параметров расчетной модели, так как ее спектр содержит все параметры собственных колебаний ДДС (коэффициенты демпфирования, частоты и формы собственных колебаний).

Соотношения (4) представляют физическую зависимость между компонентами вектора восстанавливающих сил R ( t ) и вектора перемещений Y ( t ) конструктивно-нелинейной системы. Уравнения (1)–(5) являются математической моделью колебаний такой системы при запроектном воздействии, моделируемом внезапно удаленным конструктивным элементов (колонной).

Система разрешающих уравнений динамической реакции расчетной модели до удаления колонны (БМ) при t е [ 1 ₀, 1 1 ] принимает вид [26]:

Y ( t ) = 2Re { X ( t ) } + Y st , Y ( t ) = 2Re { SX ( t ) } , Y ( t ) = 2Re { S ² X ( t ) } + M ^{- 1} P ( t ) , где

^      (6)

X (t) = X0 (t- to)+ ZP (t- to),

X ^{o (} t ^- t o ^{) =}       _

= Ф ( t - 1 o ) U -¹ М [- S ( R o ( t o ) — Y st ) + Y o ( t o ) ], ’ Z P ( t - 1 o ) = U -¹ j Ф( t -t) ^T P (t)dt.

t o

В этих уравнениях матрица U является характеристикой решения матричного квадратичного уравнения (5). Выражение реакции при свободных колебаниях в вектор-функции X ( t-t ₀) зависит от начальных условий задачи (2). Если в момент разрушения колонны (при t 0 ) БМ находилась в состоянии покоя, то Y ₀( 1 ₀) = 0, Y o ( 1 ₀) = 0 и реакция X ⁰( t-t ₀) содержит только статические перемещения (вектор Y st ).

Выражение реакции при вынужденных колебаниях выражается интегралом Дюамеля, определяемым вектор-функцией Z^P ( t-t ₀). Характер динамической нагрузки импульсного типа задается вектором P ( t ). В момент времени t = t 1 расчетная модель переходит в поврежденное состояние.

При переходе в режим колебаний поврежденной модели происходит замена внешних динамических параметров (матриц M , C , K ), сформированных до повреждения системы, на «новые» параметры (матрицы M 1 , C 1 , K 1 ), соответствующие моменту времени t ₁, при котором происходит удаление колонны. Одновременно с этим формируются векторы начальных условий (перемещений и скоростей), назначаемые из предыдущей системы уравнений (6), (7) в конце интервала t = 1 1 :

Y > ( 1 1 ) = Y ( 1 1 ), Y o ( 1 1 ) = Y ( 1 1 ).

Система уравнений динамической реакции

ПМ при ( t >  1 1 ) имеет вид:

Y(t) = 2Re{X(t)} + Yst (ti),

Y ( t ) = 2 ^R e { S i X ( t ) } ,

Y ( t ) = 2Re { S 1² X ( t ) } + M 1 - 1 P ( t ) ,

где

X ( t ) = X 0 ^{( t -} t i ) ⁺ Z P ^{( t - 1} ₁ ^), X 1⁰ ( t — 1 1 ) = ф 1 ( t — 1 1 ) U ^-1 M 1 X <— S i ( Y o ( t i ) — Y st ( t i ) ) + Y ( t i ) ] , Y_st ( t i ) = K i^-1 Q ,

t

Z P ( t - t i ) = U i^-1 J Ф 1 ( t -t) ^T P (t)dt. t i

Компонентами вектора Y st ( t 1 ) являются статические перемещения ПМ.

При анализе ПМ помимо количественных оценок значительный интерес представляют качественные оценки параметров динамической реакции в критической точке t1. Для параметров (4), (6)–(9) получены уравнения векторных невязок, записанные в виде разности динамической реакции после (уравнения (8), (9)) и до (уравнения (6), (7)) выключения колонны. Тогда величина скачков при t1 в аналитическом виде записывается так:

A Y (ti ) = 0, A Y (ti ) = 0,AY(ti) = A(M-1 K)■ Yo (ti) +

+a ( m -¹ c ) ■ Y o ( t i ) - a ( m -¹ P ) ,

AI (ti ) = AR (ti ) + AF (ti ) + AP (ti),AR (ti ) = -AK ■ Yo (ti), AF (ti ) = -AC ■ Yo (ti), где невязки

A K = K - K i , A C = C - C i , a ( M ^-1 K ) = ( M ^-1 K - M _i ^-1 K J ) , a ( M ^-1 C ) = ( M^-1C - M _i ^-1 C _i ) , a ( M ^-1 P ) = [ M ^-1 P ( t ^- ) - M f¹ P ( t + )], A P ( t i ) = P ( t i^- ) - P ( t i ⁺ ),

построены для матричных величин при t 1 до и после удаления колонны; t f , t + - критическое время 1 1 , рассматриваемое соответственно до и после выключения колонны.

Из формул (10) следует, что перемещения и скорости при t ₁ не имеют скачков, являясь непрерывными функциями времени, что обусловлено постановкой начальных условий. Остальные параметры динамической реакции в общем случае имеют скачки.

Результаты, анализ

Проведен динамический анализ 2-этажного железобетонного каркаса при запроектном воздействии, произошедшем в результате случайного наезда транспортного средства на угловую колонну (рис. 1а). Параметры каркаса: план здания 30 x 12 м, высота колонн этажей: h ₁ = 4,2 м, h ₂ = 3,3 м; шаг сетки колонн l = 6 м, поперечное сечение 0,4 х 0,4 м.

Жесткости колонн на изгиб и кручение: EJ_x = EJ y = 501330000 кНсм²; GJ = 336900000 кНсм² ( G = 0,35 E [27]).

Массы и моменты инерции плит перекрытий этажей:

m 1 = 1,97 кН ^ с²/см, m 2 = 1,82 кН ^ с²/см;

J 1 = 1713900 кН ^ см ^ с², J г = 1583400 кН ^ см ^ с².

Координаты центра жесткости (ц. ж.) O 1 1-го этажа ПМ, отсчитываемые от центра тяжести (ц. т.) C 1 , равны a 1 = 35,29 см, b 1 = 38,24 см (рис. 1б).

Для каркаса принята сдвиговая модель, согласно которой плиты перекрытий – абсолютно жесткие диски, колонны – упругие, невесомые и несжимаемые стойки с жестким защемлением в верхней и нижней части. Каждый этаж имеет 3 степени свободы: поступательные перемещения в направлении координатных осей x и y и вращательное движение, относительно вертикальной оси, проходящей через ц.ж. упругих связей (см. рис. 1а).

Матрица масс: М = diag ([ m 1 , m 1 , m 2 , m 2 , J 1 , J 2 ]).

Матрицы жесткости K , K 1 обеих расчетных моделей (БМ и ПМ) сформированы с помощью соответствующих матриц податливости L , L ₁ с использованием фундаментального соотношения K = L ^–1, K 1 = ( L 1 )^–1:

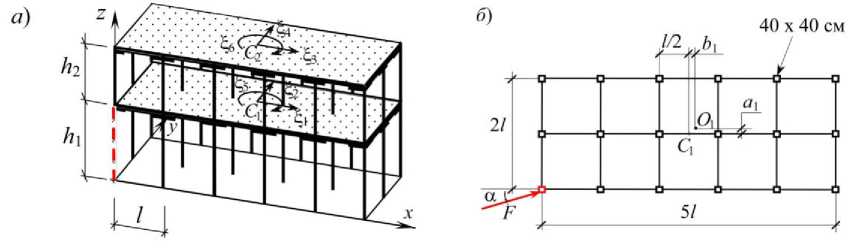
Рис. 1. Расчетная модель 2-этажного железобетонного каркаса: а – расчетная динамическая модель; б – сетка колонн

	_ 0,378       0   - 0,232       0             0             0
	0   0,378       0   - 0,232            0            0
	- 0,232       0   0,232       0            0            0
K =		x 1e+04, кН/см (кН - см);
	0   - 0,232       0   0,232            0            0
	0       0       0       0   491080,625   - 301089,917
	_      0       0       0       0   - 301089,917   301089,917 _
	_ 0,370       0   - 0,232       0         4,870             0"
	0   0,370       0   - 0,232        - 5,276            0
	- 0,232       0   0,232       0            0            0
K =		x 1e+04, кН/см (кН - см).
1	0   - 0,232       0   0,232            0            0
	4,870   - 5,276       0       0   491769,301 - 301089,917
	_      0       0       0       0   - 301089,917   301089,917 _

Силы сопротивления при колебаниях каркаса учтены по модели непропорционального демпфирования [26]:

C = (KT + TK)/2, где T = у JmK- = diag(A 11, ... , A tn); Atj = — (j' = 1, ... , n); Wj =       - частота собственных колебаний соот- wj                    mj ветствующей консервативной системы; у = 8 / п; 8 = 0,2 - логарифмический декремент колебаний; матрица Kd = diag (r11, ... , rnn) содержит диагональные элементы матрицы жесткости K.

Ударная нагрузка на колонну каркаса составила F = 50 кН при угле наклона вектора F к горизонтали а = 30 ° (см. рис. 1б). Ее воздействие на узлы расчетной схемы моделируется в виде синусоидального закона

P (t) = P 0-sin (nt), ta где P0 – вектор амплитуд, ta – время действия ударной нагрузки.

Векторы амплитуд внешних воздействий и векторы нагрузки в критической точке t 1 соответственно до ( t - ) и после ( t + ) удаления колонны принимают вид (вектор Q в (1) принят равным нулю):

	’ 15,588 ’			’  9,163  ’			’  9,163  ’
	9, 000			5, 290			5, 290
	0			0		P ( t + ) =	0
P 0 =	0		P ( t 1 - ) =	0			0
	4146,926	кН		2437,502	кН		2316,443	кН
	_       0       _	(кН·см),		_       0       _	(кН·см),		_       0       _	(кН·см)

По результатам расчета собственных колебаний базовой и поврежденной моделей, проводимых на основе процедуры решения матричного квадратичного уравнения (5), получены при n = 6 частотные спектры и коэффициенты демпфирования, приведенные в таблице.

Частоты и коэффициенты демпфирования расчетных моделей 2-этажного каркаса

№	Частоты собственных колебаний, рад/c		Коэффициенты демпфирования, рад/c
	БМ	ПМ	БМ	ПМ
1	18,170	17,702	0,274	0,260
2	18,170	17,738	0,274	0,262
3	22,207	22,264	0,335	0,337
4	53,478	53,235	2,257	2,254
5	53,478	53,238	2,257	2,255
6	65,314	65,337	2,757	2,757

Из таблицы видно, что в целом спектр частот БМ превышает спектр ПМ, а формы собственных колебаний БМ демпфируются несколько сильнее форм ПМ, что характерно для более повышенной жесткости БМ.

Анализ колебаний расчетной модели проводится в соответствии с методом альтернативного подхода [8, 10], согласно которому одна из угловых колонн каркаса считается удаленной (при t 1 ), после чего оценивается устойчивость к разрушению оставшейся структуры. Для этой цели используются системы разрешающих уравнений реакции БМ (6), (7) на интервале времени t е [ 1 ₀, 1 1 ] и уравнений реакции ПМ (8), (9) при t >  1 1 , полагая, что 1 ₀ - это время начала наезда транспортного средства на угловую колонну.

Время, при котором происходит удаление колонны, принято равным 1 1 = 0,8 t a = 1,2 c ( t a = 1,5 c). Шаг временного анализа равен A t = ta I 500 = 0,003 с. При t a = 1,5 c внешнее воздействие является кратковременной ударной нагрузкой ввиду t a > 2,5 T i = 0,864 c (см. таблицу) [27].

На рис. 2, 3 приведены кинематические и силовые параметры динамической реакции БМ и ПМ первого этажа каркаса вдоль оси x : кинематические характеристики (перемещения, скорости и ускорения) на рис. 2, силовые (восстанавливающие, диссипативные и инерционные силы) на рис. 3. На всех графиках параметры реакции БМ изображены черным цветом, для ПМ - красным цветом.

Вследствие более высокой жесткости и более повышенного демпфирования БМ для всех пара-

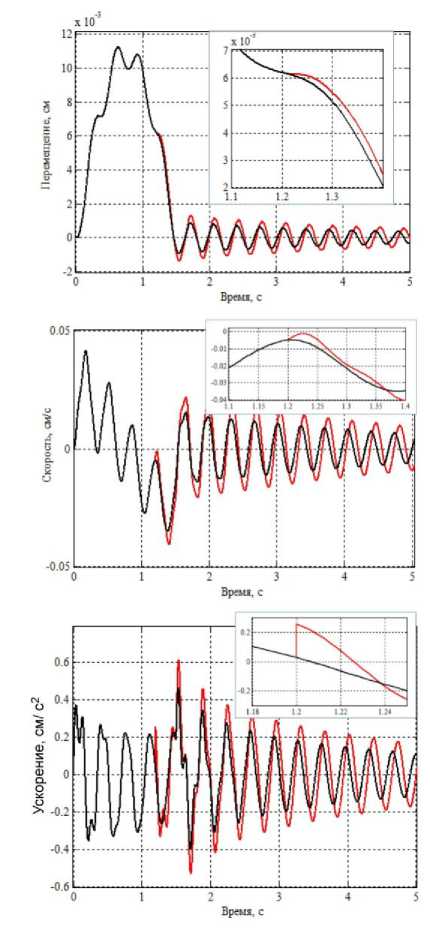
Рис. 2. Кинематические параметры реакции в ц. т. плиты перекрытия 1-го этажа (по направлению оси x )

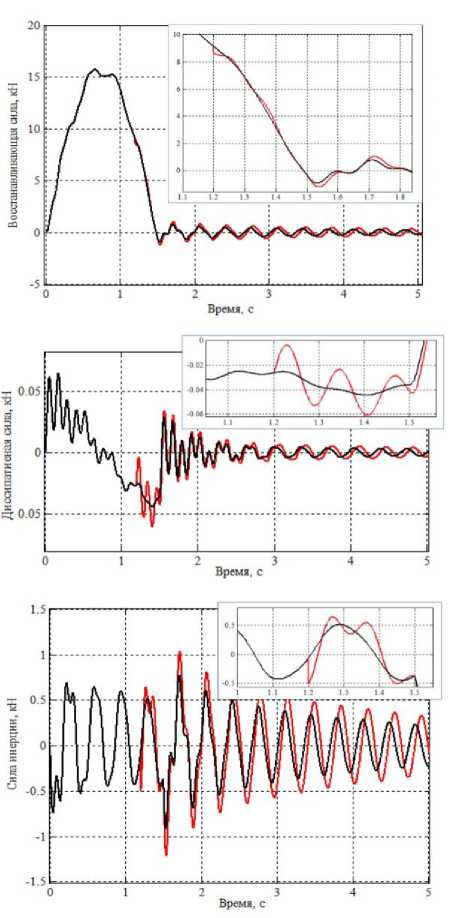
Рис. 3. Силовые параметры реакции, действующие в ц. т. плиты перекрытия 1-го этажа (по направлению оси x )

метров реакции характерно некоторое отставание кривых БМ от соответствующих кривых ПМ и снижение амплитуд БМ по сравнению с амплитудами ПМ.

На осциллограммах ускорений (см. рис. 2) и всех силовых параметрах реакции (см. рис. 3) при 1 1 ПМ каркаса содержит скачки, согласующиеся со значениями, полученными по аналитическим выражениям невязок (10), (11). Перемещения и скорости при 1 1 в ПМ скачков не имеют. На некоторых осциллограммах параметров реакции (ускорения, диссипативные и инерционные силы) сразу после разрушения колонны на небольшом интервале времени (в пределах t е [1,2; 1,5] с) наблюдаются обертональные всплески, характеризуемые повышенными амплитудами и подключением к основному тону колебания ПМ более высокочастотных гармоник.

Угловые параметры горизонтальных колебаний (перемещений и скоростей), связанные с вращением плиты перекрытия 1-го этажа, даны на осциллограммах рис. 4. Поворот перекрытия происходит вокруг ц. ж. O 1 .

В плите перекрытия 1-го этажа возникает крутящий момент от действия внешних горизонтальных сил относительно ц. ж. О 1 , вызывающий ответную реакцию - внутренние моменты от восстанавливающих, диссипативных и инерционных сил. На 2-м этаже крутящие моменты отсутствуют из-за нулевых горизонтальных сил. На рис. 5 представлены моменты восстанавливающих (упругих) и инерционных сил, действующие в базовой и поврежденной моделях 1-го этажа.

Скачки на осциллограммах крутящих моментов от действия восстанавливающих и инерционных сил (см. рис. 5) появились в плите перекрытия 1-го этажа вследствие образования эксцентриситетов a 1 , b i между ц. т. C i и ц. ж. O i упругих связей этажа ПМ (см. рис. 1б). Из формул (10), (11) следует, что наличие эксцентриситетов привело к появлению ненулевых невязок матриц жесткости и демпфирования ( A K , A C ), а также невязки вектора нагрузки в критической точке 1 1 : A P ( 1 1 ) = P ( t - ) - P ( t + ) с ненулевой 5-й компонентой (см. (12)). Невязки приведенных величин появились только после разрушения колонны, поэтому на всех осциллограммах до экстремального события (при t ₁ = 1,2 с) динамические реакции БМ и ПМ совпадают между собой.

На рис. 6 даны осциллограммы горизонтальных перемещений (по оси x ) и ускорений (по оси у ) плиты перекрытия расчетных моделей 2-го этажа. Хотя ц. т. C₂ и ц. ж. O ₂ во 2-м этаже совпадают друг с другом, на осциллограмме ускорений при 1 1 = 1,2 с имеется скачок. Это позволяет сделать вывод о том, что удаление связи в каком-либо одном этаже каркаса приводит к изменению жесткости всей системы, а значит, и к изменению параметров динамической реакции на других этажах каркаса.

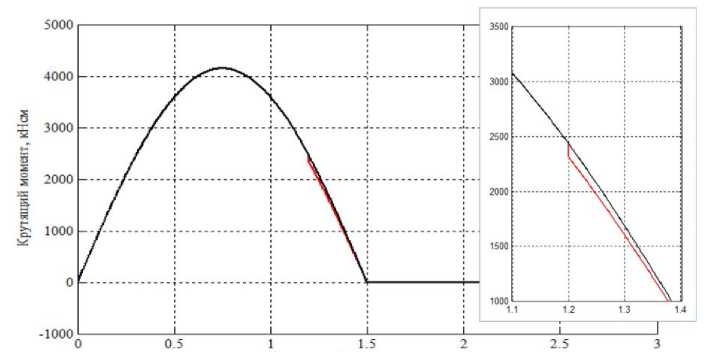
На рис. 7 показан крутящий момент P ₅( t ) в 1-м этаже плиты перекрытия. В ПМ крутящий момент имеет скачок, причина которого, как уже отмечено - внезапное изменение положения координат ц. ж., изменившее плечо горизонтальной силы. Значение скачка крутящего момента в ПМ опреде-

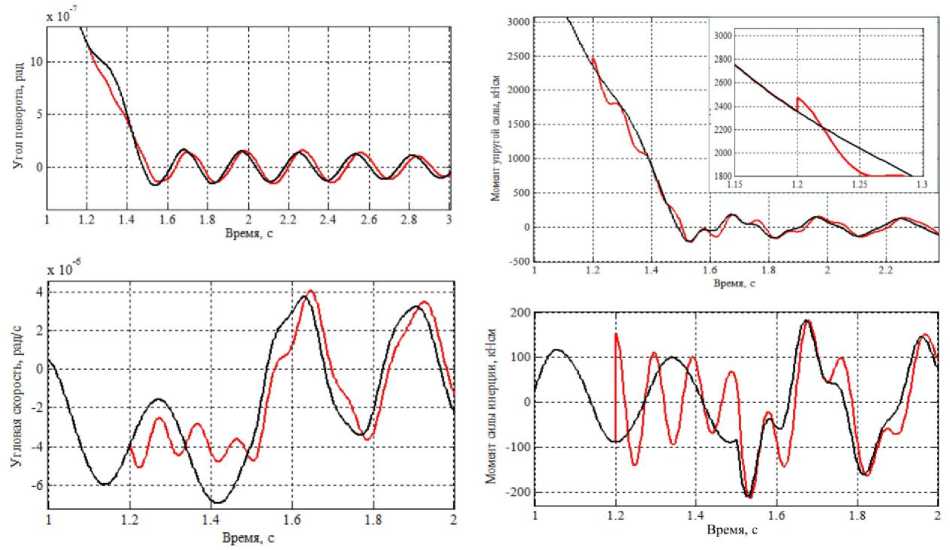
Рис. 4. Угловые параметры реакции плиты перекрытия 1-го этажа

Рис. 5. Моментные характеристики реакции, действующие в плите перекрытия 1 -го этажа

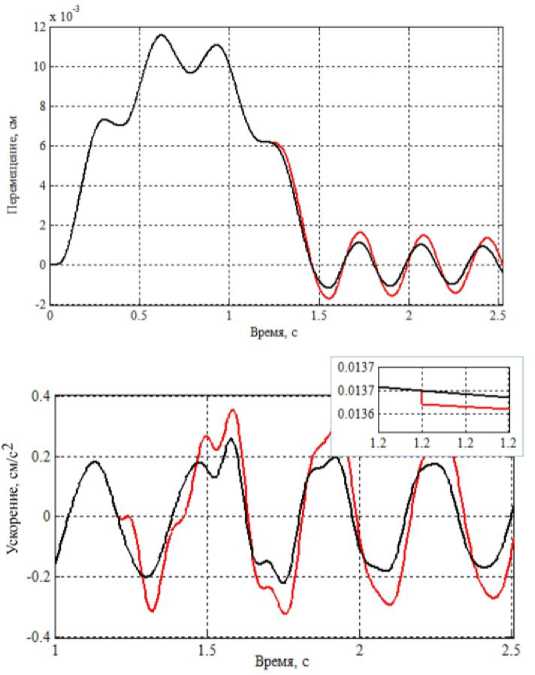
Рис. 6. Параметры реакции во 2-м этаже каркаса: горизонтальное перемещение ц. т. C 2 по оси x ; ускорение плиты перекрытия по оси y

Время, с

Рис. 7. Крутящий момент от действия внешней горизонтальной силы в 1-м этаже расчетных моделей каркаса (БМ и ПМ)

ляется разностью (12): A P ₅( t ) = P ₅( t i ) - P ₅( t + ) = 121,058 кН - см.

Для оценки решения введены вектор-функции:

Ф ( t ) = R ( t ) + F ( t ) - I ( t ),        A ( t ) = ф ( t ) - P ( t ).

Первая величина ф(t) - суть алгебраическая сумма всех сил левой части ОДУ (1); она дает качественную оценку приближения построенного решения к заданной вектор-функции P (t) внешних воздействий. Вторая A(t) является векторной невязкой между построенной левой и заданной правой частями ОДУ (1) и служит критерием точности решения.

На рис. 8 приведен суммарный крутящий момент ф ₅( t ), вызванный действием внутренних сил левой части ОДУ в 1-м этаже. Величина ф ₅( t ) выражает степень приближения решения к функции заданной нагрузки P ₅( t ).

Левый фрагмент: скачок у крутящего момента ПМ при t1 = 1,2 с. На правых фрагментах показаны свободные колебания моделей при t1 ≥ 1,5 с, когда внешняя нагрузка отсутствует. Здесь значения крутящего момента близки к нулю: для ПМ по- грешность не превышает: ε ≤ 3e–09 (красный цвет на верхнем фрагменте), для БМ – ε ≤ 2e–13 (черный цвет на нижнем фрагменте).

На рис. 9, 10 приведены осциллограммы функциональных невязок ∆ 1 ( t ) и ∆ 5 ( t ) соответст-

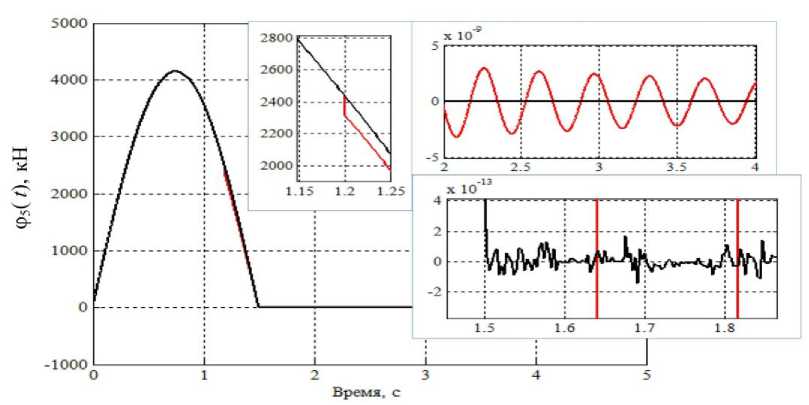
Рис. 8. Функции ϕ 5 ( t ) левой части ОДУ движения (1) расчетных моделей каркаса (БМ и ПМ) – суммарный крутящий момент в 1-м этаже

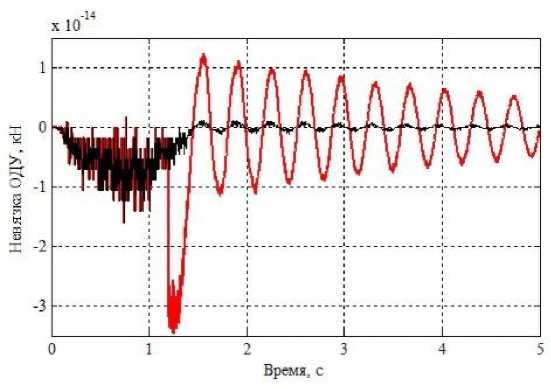
Рис. 9. Осциллограммы невязки ∆ 1 ( t ) ОДУ (1) горизонтальной силы, действующей в ц. т. плиты перекрытия 1-го этажа вдоль оси x

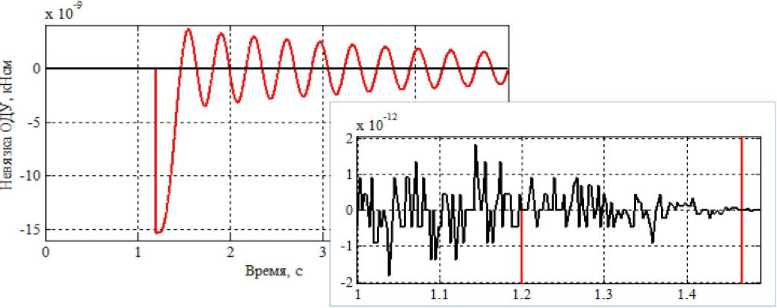
Рис. 10. Осциллограммы невязки ∆ 5 ( t ) ОДУ (1) для крутящего момента в плите перекрытия 1-го этажа расчетных моделей каркаса

венно суммарной горизонтальной силы, действующей в ц. т. C 1 вдоль оси x , и крутящего момента в плите перекрытия 1-го этажа. В обоих случаях осциллограммы невязок показывают высокую точность решения. Для кривых ∆ 1 ( t ) на рис. 9 точность интегрирования ОДУ движения (1) по обеим расчетным моделям не превышает ε ≤ 3,5^.10^–14 кН, для кривых ∆ ₅( t ) (рис. 10) величина погрешности: ε ≤ 15^.10^–9 кНсм.

Результаты, приведенные на рис. 7–10, свидетельствуют о высокой точности построения динамической реакции каркаса с внезапно выключенной колонной на основе временного анализа.

Выводы. Заключение

• 1.    Анализ отечественных и зарубежных источников показывает, что подавляющее большинство исследований по моделям разрушения основано на численных и экспериментальных методах. Специалистами отмечен дефицит теоретической базы в разработке основ механизма живучести конструктивных систем, без создания которой невозможно получить строго обоснованные предложения для их включения в нормативные документы.

• 2.    Построена математическая модель конструктивно-нелинейных колебаний системы с внезапно выключающимся элементом при нагрузке, моделирующей запроектное воздействие. Разрешающие уравнения динамической реакции, сформированные с помощью временного анализа, учитывают поведение расчетной модели как до, так и после ее повреждения.

• 3.    В анализе 2-этажного железобетонного каркаса при внезапном удалении угловой колонны 1-го этажа у вектора внешних динамических сил ПМ обнаружен эффект скачка (для компоненты крутящего момента 1-го этажа), появившийся вследствие изменения положения координат ц. ж. этажа.

• 4.    Показана эффективность метода решения задачи конструктивно-нелинейных колебаний каркаса при использовании теории временного анализа ДДС. В рамках предложенной математической модели оценка точности интегрирования дифференциального уравнения движения ПМ каркаса не превышает значений: 3,5^.10^–14 кН (для линейной составляющей невязки ∆ 1 ( t )) и 15^.10^–9 кН·см (для невязки крутящего момента ∆ 5 ( t )).

Предложенный аналитический аппарат открывает возможности для более глубокого и детального анализа конструктивно-нелинейных систем при критических ситуациях отказа несущих элементов и позволяет выявлять скрытые резервы в оценке механизма живучести этих систем.

Разработка более совершенных расчетных моделей, апробированных в аналитических подходах, может найти применение в создании расчетных схем анализа численных методов, включая МКЭ. Учет новых знаний в основе механизма процессов, связанных с внезапными отказами критических элементов, способен качественно изменить ситуацию в области расчета конструкций при запроектных воздействиях.