Анализ конструктивно-нелинейных колебаний железобетонного каркаса

Обзор литературы

Прогрессирующее обрушение является одним из наиболее опасных вариантов разрушения на стадии возведения и эксплуатации здания. При отказе одного из структурных элементов (балки, колонны, подкоса и т. д.) происходит лавинообразное обрушение всего здания, что влечет за собой большие человеческие жертвы и экономические потери.

Обеспечение безопасности строительных конструкций закреплено в Федеральном законе № 384-ФЗ [1]. Рекомендации по обеспечению надежности также закреплены в нормативной документации [2–4]. В отечественных строительных нормах установлено, что расчет прогрессирующего обрушения [5] должен носить вариативный характер, т. е. рассматриваются несколько возможных сценариев разрушения конструкций. При этом расчет должен производиться с коэффициентами запаса как для особого воздействия [6]. Расчет на прогрессирующее обрушение сводится к оценке площади возможного локального разрушения в зависимости от этажности здания. Происходит удаление несущих элементов конструкции с повторным расчётом каркаса. В документе [7] даются подробные указания и рекомендации для проектирования и строительства высотных зданий на устойчивость против прогрессирующего обрушения.

При сейсмическом воздействии предложена методика, заключающаяся в замене внезапно выключенной связи импульсным воздействием, величина которого равна значению усилия в связи перед ее удалением [8]. Статические подходы при выключении связей использовались для оценки динамических эффектов в стержневых системах из хрупких материалов [9], при расчёте зданий на прогрессирующее обрушение с помощью «множителя» для учета инерционного эффекта [10].

В статьях [11, 12] отмечен факт расплывчатости формулировок в отечественных нормах и необходимость их качественной доработки.

Аналитические подходы к расчету конструкций с разрушающимися связями ввиду своей сложности используются крайне редко [13, 14]. В [13] проводился анализ металлических структур с выключающимися элементами при использовании разложения решения по формам собственных колебаний в среде MathCad без учета внутреннего трения материала. В [14] использовался метод де- композиции при моделировании динамических догружений железобетонного многоэтажного каркаса, вызванных его структурной перестройкой. Это позволило выявить параметры динамического отклика подконструкции, моделирующей зону возможного локального разрушения элементов каркаса здания при внезапном удалении одной из несущих конструкций в этой зоне.

Согласно европейским нормам [15], прогрессирующее обрушение считается исключительным явлением, для которого на данный момент не разработано приемлемых методов предотвращения. Для зданий высотой менее 10 этажей рекомендуется проводить статический линейный анализ, для иных случаев – нелинейный динамический анализ.

В основе норм США GSA (для государственных зданий) и UFS (для гражданских зданий) лежит системный анализ рисков [16, 17]. Для конструкций повышенной этажности c несимметричными конструкциями строительные нормы предлагают использование нелинейного статического и динамического анализа. Оба документа рассматривают условное удаление нагруженного несущего элемента каркаса. Предлагаются рекомендации по учету влияния появляющихся пластических шарниров, коэффициенту динамичности (равному 2,0), а также по увеличению коэффициента деформационного упрочнения материала, отражающего повышение прочности бетона во времени.

В обзорной статье [18] обобщен многолетний опыт зарубежных исследований в области оценки разрушающихся связей и выделено 4 основных направления по разработке методов живучести конструкций. Это методы оценки надежности нелинейных моделей разрушения для 2D- и 3D-каркасов; разработки мероприятий по повышению сопротивляемости системы к разрушению, создание вероятностных моделей по оценке риска возникновения выключающихся связей; разработки стойких к разрушению конструкций с опорой на результаты теории сейсмостойкости.

• 1.    Методы оценки надежности конструкций на основе нелинейных моделей разрушения с применением плоских 2D- и объемных 3D-каркасов

• 2.    Разработка мероприятий по повышению сопротивляемости системы к разрушению

• 3.    Создание вероятностных моделей по оценке риска возникновения выключающихся связей

• 4.    Разработка конструкций, стойких к прогрессирующему обрушению, основанных на результатах теории сейсмостойкости

На примере моделирования взрыва показано [19], что сама взрывная волна внутри здания не так опасна для конструкции, как выключающиеся из работы элементы. В [20] проводились исследования в железобетонной балке. Показано, что балка подвергается более серьезному растрескиванию по глубине и получает большие деформации и внутренние усилия, когда ударная нагрузка прикладывается перед последующим взрывным нагружением. После удара на стадии свободных колебаний балка получает большее повреждение от взрыва, нежели в любом ином случае.

На основе уравнения энергетического баланса разработан механизм образования прогрессирующего обрушения [21, 22]. Исследованы оценки живучести зданий при разработке аналитического подхода по определению коэффициента динамичности [22, 23], при создании моделей с новыми возводимыми конструкциями [24, 25]. Также в экспериментальных исследованиях по оценке живучести показано [26, 27], что для более высокой этажности и малом пролете зданий характерна более высокая стойкость к разрушению.

В работе [28] показано влияние моделирования конструкций, помимо основного каркаса (колонны и балки), позволяющее точнее описать процесс перераспределения энергии в системе. Проведен ряд исследований, в которых существенную роль может играть толщина плит перекрытия [29], их конструкция [30] и способы армирования, в частности, в [31] показан симметричный вариант армирования плиты, обеспечивший повышенную сопротивляемость системы к разрушению. Также заметное влияние в этом плане могут оказывать исследования соединений типа балка – колонна [32, 33].

В статье [34] исследованы вариативные оценки влияния силы, формы, длительности взрывной волны, позволяющие оценивать наиболее опасный сценарий развития событий при разрушении надземных конструкций. Важнейшим фактором является характер действующей нагрузки. Так, в работе [35] экспериментально показано, что балки при статическом способе моделирования нагрузки работали значительно хуже, чем при динамическом способе моделирования (разница в работе балок при оценке динамического коэффициента составляла 25 %).

Наиболее частыми в работах встречаются случаи разрушения крайней или угловой колонн первого этажа. Особенно опасным считается разрушение угловой колонны и соседних с ней колонн [32, 36]. В [37] отмечено, что подвергаться оценке может не только каркас в целом, но и отдельные его элементы, например, балки.

В ряде работ [32, 38] отмечено, что здания, проектируемые для районов с высокой сейсмично- стью, оказываются стойкими к прогрессирующим обрушениям. Отдельное внимание в статье [28] уделено верхним этажам, так как они проектируются при условии меньшей несущей способности относительно нижних этажей.

Отметим общие замечания по приведенным фактам обзора литературных источников, характерные как для отечественных, так и зарубежных работ.

Из приведенных материалов по моделям разрушения можно выделить важные моменты, касающиеся сложности моделирования процесса структурной перестройки на основе численных методов для линейных и нелинейных моделей. Нелинейные модели разрушения способны обеспечивать более точное прогнозирование реакции системы по сравнению с линейными моделями. Но такие модели, как правило, являются дорогими коммерческими проектами, требующими более сложного программного обеспечения и значительных вычислительных ресурсов, связанных с финансовыми и временными последствиями [30].

По этой причине рядовыми инженерами-конструкторами используются в основном упрощенные методики анализа, базирующиеся обычно на экспериментах, в которых основные режимы механизмов разрушения реализуются только для откалиброванных конструктивных систем с жесткой расчетной схемой сооружения. Для общих расчетных моделей эти режимы малопригодны ввиду неопределенного характера информации, что исключает возможность оценки их резервной мощности [30].

Рекомендации по использованию различных статических «множителей» (в работах [10, 23] приводятся значения 1.5, 2.0) для учета инерционных эффектов являются малосостоятельными, так как не отражают реальный динамический эффект в конструкции. В большинстве случаев исследуется не процесс деградации конструктивного элемента (колонны), а последующий эффект, вызванный процедурой мгновенного удаления несущего элемента (колонны). То есть моделируется не само экстремальное событие, а его следствие посредством внезапного выключения элемента из работы [8, 39].

Из обзорных источников следует, что подавляющее большинство исследований по моделям разрушения основано на численных методах и экспериментах. В отечественных и зарубежных публикациях наблюдается дефицит теоретической базы для обоснования принципов прогрессирующего обрушения, отсутствует разработка аналитических моделей для глубокого и детального изучения вопроса. Автором статьи [40] справедливо отмечено, что «отсутствуют аналитические методы определения начальных повреждений и прогнозирования вероятности последующего лавинообразного обрушения сооружения из-за предполагаемых аварийных воздействий. Невозможно ис- пользовать численные методы расчета МКЭ ввиду отсутствия подробных знаний поведения конструкций при лавинообразном обрушении…».

В статьях [41, 42] в рамках теории временного анализа разработан общий подход к построению динамической реакции диссипативной системы при выключении (разрушении) конструктивного элемента (связи). Этот процесс рассматривается в двух вариантах, когда ситуация с разрушением конструктивного элемента возникла в положении статического равновесия системы (до разрушения элемента система находилась в покое). При втором варианте выключению конструктивного элемента предшествовал процесс колебаний, то есть до разрушения система находилась в движении.

Для этой цели используется теория временного анализа дискретных диссипативных систем (ДДС), основанная на исследовании характеристического матричного квадратного уравнения (МКУ) [43]. Предлагаемый подход обладает достаточно широкой областью приложения и позволяет с единых позиций использовать разработанные математические модели с линейной и нелинейной восстанавливающей силой.

Общие замечания

В соответствии с [41] приведено изложение теоретических основ колебательного процесса конструктивно-нелинейной системы, которая представлена как ДДС. Рассмотрено внезапное разрушение связи, вызванное действием статической и динамической (ударной или импульсной) нагрузок.

Пусть внезапное выключение связи происходит в некотором j -м конструктивном элементе системы. Всякое разрушение связи представляет деструктивный процесс, приводящий к изменению (ослаблению) жесткости расчетной динамической модели. Это немедленно ведет к нарушению баланса между внешними и внутренними силами расчетной модели. Действительно, вместе с разрушенной связью происходит одновременное исчезновение усилия, действующего в данной связи, что приводит к нарушению статического и динамического равновесия системы.

Возникшая диспропорция между внешними и внутренними силами может быть преодолена только за счет быстрой перестройки конструкции путем включения всех её внутренних резервов (хотя бы в той области или зоне конструкции, где произошло разрушение связи). Такая перегруппировка, учитывая внезапный характер деструктивного процесса, не может протекать статическим путем. Если система до разрушения связи находилась в состоянии покоя, то для сохранения своей целостности она вынуждена перейти в состояние движения, сопровождающееся возникновением динамических сил, включающих силы инерции и силы внутреннего трения. Это необходимое условие для создания нового баланса сил. Если же до разрушения связи система уже совершала колебания, то теперь ее движение будет направлено на повышение резервных мощностей системы, основная цель которого – также перегруппировка внутренних сил.

При этом важно отметить, что характер движения системы зависит от ее резервов прочности в поврежденном состоянии. В зависимости от несущей способности конструкции последняя может совершать как колебательное, так и неколебательное движение. При условии сохранения резерва прочности поврежденной конструкции узлы последней будут совершать свободные затухающие колебания (рис. 1а). С течением времени, когда колебания прекратятся, в системе установится новое положение статического равновесия. Если же сопротивляемость системы к разрушению окажется не обеспеченной, то продолжится дальнейшее последовательное выключение связей и процесс разрушения примет необратимый характер (рис. 1б).

При разрушении связи жёсткость j -го конструктивного нелинейного элемента системы внезапно изменяется, переходя с одного уровня на другой. На диаграмме деформирования «Восстанавливающая сила – относительное перемещение»: R j ( t ) ~ y j ( t ) (см. рис. 1а) показаны два уровня жёсткости j -го элемента в момент выключения связи при t 1 . Данные уровни определяются тангенсами углов наклона прямых ab и cd к горизонтальной оси. Прохождение прямых через начало координат говорит об упругом процессе колебаний системы в каждом состоянии. Скачок в восстанавливающей силе на диаграмме, появившийся вслед-

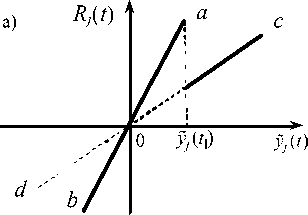
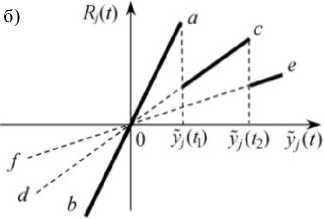
Рис. 1. Диаграмма деформирования j -го конструктивно нелинейного элемента системы с выключенными связями: а – с одной; б – с несколькими выключенными связями

ствие выключения связи и снижения жёсткости, не создает разрывов в относительных перемещениях j -го конструктивного элемента. Свойства непрерывности относительных перемещений данного элемента передаются в целом и на абсолютные перемещения узлов всей системы.

На рис. 1б показано более двух уровней жёсткости j -го элемента при выключении связей в моменты времени t ₁, t ₂, … , соответствующие тангенсам углов наклона прямых ab , cd , ef , … к горизонтальной оси. При недостаточном резерве прочности поврежденной конструкции колебательный процесс перейдет в монотонное апериодическое движение, заканчивающееся разрушением j -го элемента конструкции, которое может оказаться фатальным для всей системы.

Метод исследования

Построение динамической реакции системы проводится в рамках теории временного анализа для конструктивно-нелинейной задачи, задаваемой диаграммой деформирования с одной выключенной связью (см. рис. 1а). Условия динамического равновесия системы имеют следующие временные этапы: до момента разрушения связи ( t е [ t 0 , t 1 ]), момент разрушения связи (при t 1 ) и после разрушения связи ( t >  t 1 ), где t 0 - время начала временного анализа.

При формировании уравнений реакции системы необходимо учитывать, что на интервале времени t е [ t 0 , t 1 ] колебания ДДС происходят при «старых» параметрах расчетной динамической модели (РДМ), то есть при матрицах масс M , демпфирования C и жёсткости K , формируемых для неповрежденной системы при t ₀ = 0. Жесткость системы для этого случая соответствует прямой ab диаграммы деформирования на рис. 1а. Векторы начальных перемещений и начальных скоростей для данного интервала времени имеют вид: Y = Y ( t о ) , Y o = Y ( t о ) ^.

В момент выключения связи при t ₁ происходит замена «старых» параметров РДМ на «новые» – матрицы M 1 , C 1 , K 1 , формируемые при t 1 и соответствующие прямой cd на рис. 1а. Этот переход сопровождается обязательной сменой начальных условий: Y = Y ( t j ) , У _о = Y ( t _j ) , которые формируются из уравнений реакции системы в конце предыдущего интервала времени при t = t 1 .

Согласно линейной модели упруговязкого сопротивления, уравнение движения и начальные условия динамической задачи на интервале t е [ 1 ₀, t ₁] имеют вид:

MY ( t ) + CY ( t ) + KY ( t ) = ft ), (1)

Yo = Y (tо), Yo = Y (10), (2) где M = diag (m 1, ... , mn), C = CT, K = KТ е Mn(R); Y(t) - вектор перемещений; ft) = Q + P(t) - вектор внешней нагрузки. Здесь векторы Q = KYst, P(t) представляют статическую и динамическую составляющие нагрузки, Yst – вектор статических перемещений.

Начальный этап: колебание неповрежденной системы ( t ∈ [t₀, t₁] )

В общем случае динамической задачи, представленной уравнением (1) и начальными условиями (2), уравнения реакции ДДС на интервале t е [ 1 ₀, 1 1 ] при действии ft ) = Q + P ( t ), согласно [41], имеют вид:

^Y ( t ) = 2^Re { X ( t ) } + Y st ,

■ ^Y ( t ) = ^2Re { ^SX ( t ) } ,                          (3)

Y(t) = 2Re {S2X(t)}+ M-1P(t), где

X ⁽ t ) = X 0 ^{( t-t} о ) ⁺ Z P ^{( t-t} о ) ,                    ⁽⁴⁾

X ⁰ ( t-t о ) = Ф ( t-1 о ) U- ¹ M [ -S ( Y o - Y_st )

+ YY ] ,

t

Y st = KQ^{- j} , Z^P ( t-t о ) = U^{- 1} / ф ( t- T ) ^T P ( t ) d T .

t ₀

Здесь матрица внутренних динамических характеристик системы S е M n ( С ) удовлетворяет уравнению движения собственных форм колебаний (или матричному квадратному уравнению – МКУ):

MS ² + CS + K = 0. (5)

Для упругой ДДС с малой диссипацией решение (5) представляется в виде комплексносопряжённых корней [43]:

S = M ^{- 1} ( -C + V + U ) / 2 ,

S = M "^j ( -C + V-U ) / 2, где V = -V ^T , U = U ^T ( V,iU е M n ( R ) ) .

Матричные корни S , S обеспечивают построение фундаментальных решений однородного обыкновенного дифференциального уравнения (ОДУ), которое вытекает из неоднородного ОДУ (1), и связаны с фундаментальной матрицей Ф (t) соотношением Ф (t) = eSt.

Момент разрушения связи (при t1)

В этот момент происходит структурная перестройка расчетной модели, которая с позиции математического моделирования задачи требует проведения корректировки параметров расчета. Полагая, что процесс деградации конструктивного элемента происходит мгновенно (напр., при взрыве), рассматривается сразу последующий эффект, вызванный процедурой мгновенного удаления несущего элемента (напр., колонны). Тогда при t = t ₁ будем иметь следующие параметры расчета.

Внешние динамические параметры системы (матрицы M , C , K ) заменяются на новые величины (матрицы M ₁, C ₁, K ₁; технические вопросы реализации, связанные с построением «новых» матриц, в настоящей статье не обсуждаются).

При этих параметрах из решения МКУ (5) вычисляются внутренние динамические характеристики (матричные корни S ₁, S ₁ ), обуславливающие переход конструкции в состояние поврежденной РДМ.

Векторы начальных условий (начальные перемещения и начальные скорости) примут вид

Y O = Y ( ¹ 1 ) , Y o = Y ( 1 1 ) ,                                                                                                   (6)

где правые части начальных условий получены из уравнений (3), (4) в конце интервала времени 1 е [ 1 ₀, 1 ₁].

Кроме того, в данный момент времени проводится смена индексов: в уравнениях реакции при свободных и вынужденных колебаний заменяется t 0 на t 1 .

Новый этап: колебание поврежденной системы ( 1 >  1 1 )

После корректировки параметров РДМ конструкции система разрешающих уравнений движения примет вид, сходный по форме с уравнениями реакции (3), (4) ( 1 >  1 1 ):

где ^

'Y ( 1 ) = 2Re { X ( 1 ) } + Y s1 ( 1 1 ) , Y ( 1 ) = 2Re { SX ( 1 ) } ,

( 1 ) = 2Re { S 1² X ( 1 ) } + M Г ¹ P ( 1 ) , X ( 1 ) = X 1⁰ ( 1-1 1 ) + Z P ( 1 — 1 1 ) , ^Г X ⁰ ( 1 — 1 o ) = Ф 1 ( 1 — 1 o ) U - ¹ М 1 [ -S ( Y o ( 1 1 ) - Y ( 1 1 ) ) + Y o ( 1 1 ) ] ,

Y s1 ( 1 1 ) = K — ¹ Q . Z P ( 1-1 1 ) = U 1 ^{— 1} J Ф ( 1 — T ) T P ( t ) d t .

.                                                                                ¹ 1

Элементы вектора Y_st ( t ₁) по аналогии с (4) определяют статические перемещения расчетной модели поврежденной конструкции. В качестве начальных условий (6) Y 0 , Y ₀ принимаются значения векторов перемещений и скоростей (3), (4) в конце интервала времени [ t ₀, t ₁].

В уравнениях (8) выполнены замены t ₀ на t ₁ в матричной функции Ф₁( t – t ₁), принадлежащей реакции при свободных колебаниях X 0 ( 1 - 1 1 ) , и нижнем пределе интеграла реакции при вынужденных колебаниях ^Z 1 P ^{( 1 - 1} 1 ) .

Динамическая реакция в форме (7), (8) обеспечивает замкнутое (точное) решение дифференциального уравнения движения повреждённой системы на интервале 1 е [ 1 1 , 1 2 ]. Действительно, после подстановки (7), (8) в левую часть уравнения (1) (с новыми матрицами M ₁, C ₁, K ₁) и последующей группировке слагаемых получаем ( 1 >  1 1 ):

M i [ 2Re { S 12 X ( 1 )} + M 1’¹ P ( 1 ) ] + 2 C 1 Re { S^X ( 1 )} + 2 K i [ Re { X ( 1 ) } + Y s, ( 1 1 ) ] =

= 2Re {[ M 1 S 1² + C 1 S 1 + K 1 ] X ( t )} + P ( t ) + K 1 Y st ( t 1 ) = P ( t ) + Q = f ( t ).

Частный случай формирования уравнений реакции ДДС

Системы уравнений реакции (3), (4) и (7), (8) представлены для наиболее общей предпосылки задачи, когда РДМ конструкции до начала действия динамической нагрузки P ( t ) (при t = t 0 ) находилась в состоянии движения. Рассмотрим частный случай уравнений реакции, когда РДМ конструкции до начала действия динамической нагрузки P ( t ) находилась в положении статического равновесия.

В этом случае векторы начальных условий запишутся так:

Y > = Y s1 , Y ^ o = O,                                                       (6а)

Поскольку при t = t 0 РДМ конструкции находится в состоянии покоя, то в силу (6а) вектор-функция (4) X ⁰ ( t–t 0 ) = 0. Тогда из уравнений (3), (4) получим:

'Y (1 ) = 2Re{ X (1)} + Ys1,

Y ( 1 ) = 2Re { SX ( 1 ) } ,                                                                       (3а)

Y (1) = 2Re{ S 2 X (1)} + M 1P (1),

X ( 1 ) = Z^P ( 1-1 o ) , Y_st = KQ^- p

(4а)

Z^P ( 1-1 _o ) = U^{- 1} J Ф ( 1- t ) ^t P ( t ) d t .

t 0

Системы уравнений реакции после разрушения связи (при 1 >  1 ₁) в структурном отношении будут иметь вид, совпадающий с уравнениями (7), (8).

Результаты, анализ

Рассматриваются вынужденные колебания 3этажного промышленного каркаса (рис. 2) под действием нагрузки от взрыва. Параметры расчетной динамической модели каркаса приведены в работе [43]. Матрица затухания C принята в соответствии с моделью непропорционального демпфирования

C = ( KT + TK )/2, где K , M – матри цы жесткости и масс РДМ каркаса; T = γ MK_d ^{- 1} = diag( Δ t ₁,..., Δ t_n ), K_d – диагональ-

возникают усилия: продольная сила N _ 395,2 кН, моменты М Х _ 31,7 кНм, М_у _ 29,9 кНм. Тогда

коэффициент N

395,2

« _ --- _ ------ n    Rbb^o    17,55^40^35

= 0,161.

Время конца упругой стадии определялось по формуле [44]:

t_e _ 0,5t_e2 _ 0,75 c, где t_e2 _ 1,5 с - время импульсного воздействия (взрыва).

Скорость деформаций бетона

^ b ^_

E bR _ 0,002

ная матрица, составленная из диагональных элементов матрицы K ; γ = 0,1 – коэффициент потерь.

Координаты центра жесткости O 1 1-го этажа каркаса a 1 = b 1 = l / 18 ( l = 6 м). Закон воздействия соответствует синусоидальному импульсу F ( t ) = sin ( π t / t a ) F 0 , где t a = 1,5 с – время действия им-

te 0,75

_ 0,002667 ¹ , с

пульса.

Несущая способность колонны сечением

где £bR _ 0,002 - предельные деформации бетона при центральном сжатии [45].

Тогда по табл. 3.1 [46] коэффициент повышения прочности бетона при динамических воздействиях равен ybP _ 1,17.

Согласно [45], предельные деформации арматуры определяются по формуле

b × h = 40 × 40 см, заармированной 4Ø16 мм (A_s = 4,02 см ² ), определялась как для косого вне-центренно сжатого железобетонного элемента, исходя из класса бетона В20 ( R_bn = 15 МПа), класса арматуры А400 ( R_bn = 400 МПа) с учетом харак-

_    _ ^Rsn    ⁴⁰⁰

^{S,ei —} E_s^— 200000 ^— ,    ,

где E_s - модуль упругости арматурной стали, МПа.

Отсюда скорость деформации арматуры [44]

теристик материалов при динамических воздействиях, которые определяли согласно [44].

Определение несущей способности колонны

каркаса на действие импульса

Принимая полезную высоту

сечения

E.

• _ S_s ,el _ 0,002

• <■ —      —

¹ t e 0,75

_ 0,002667 ¹ . с

h ₀ =35 см, коэффициент

Re Ac « _ ^- - ¹     R_bbh₀

428,8^4,02

17,55^40^35

0,07.

Исходя из предварительного статического

расчета, при действии статических длительных нормативных нагрузок в угловой колонне каркаса

Исходя из этого значения, по табл. 3.3 [44] коэффициент повышения прочности арматуры при динамических воздействиях равен ySP _ 1,072.

В результате определяются характеристики материалов:

бетон R_bd _ y_bPR_bn _ 15 • 1,17 ⁼ 17,55 МПа, R bt, _d _ R btn _ 1,35 МПа;

арматура       R_sd _ y_spR_s „ _ 1,072 • 400 _

428,8 МПа, R_sc , _d _ R_sn _ 400 МПа.

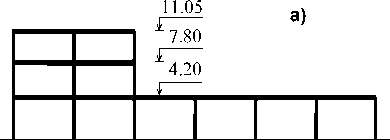
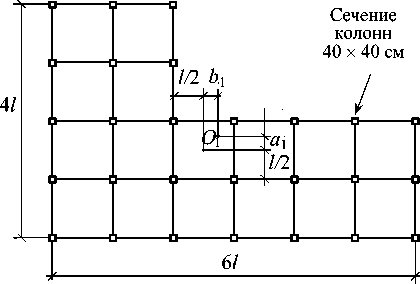
Рис. 2. Расчетная модель 3-этажного железобетонного каркаса: а – конструктивная схема здания; б – расчетная динамическая модель

б)

h 3

h 2

h 1

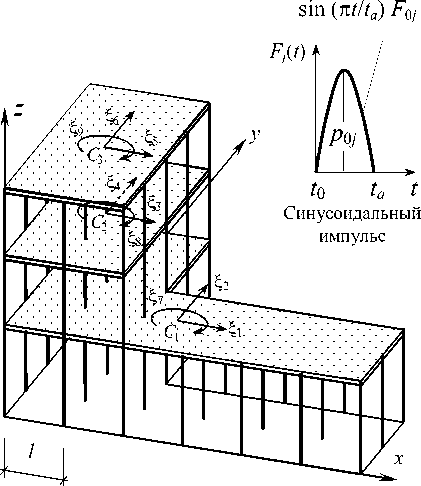
Для колонны, жестко связанной с перекрытием, максимальный момент, возникающий в ней от действия горизонтальной равномерно распределенной динамической нагрузки, составляет М = ql ² /12, действуя в уровне перекрытий. Соответствующие составляющие этого момента в зависимости от угла приложения нагрузки q к главной оси сечения колонны я:

М_х = ql ² • cos(^) /12, М ^ = ql ² • sin(a) /12. (10)

Поскольку a_s = 5 см < 0,15h₀ = 5,25 см, то, исходя из значений a_s и а_п , предельное значение коэффициента а_т = 0,12.

Тогда предельный момент, воспринимаемый сечением, при его действии вдоль сторон сечения

М ⁰ = a_mR_bbh 0 = 103,2 кНм.

С учетом того, что сечение квадратное, М $ = М ⁰ = М ⁰ = 103,2 кНм.

Поскольку колонна находится в условиях косого внецентренного сжатия, требуется учет совместного действия моментов, для этого используется известная формула норм [46]:

(«г ^(.^ ) * _S1.

в которой М_х , М_у - моменты от внешней динамической нагрузки q относительно центра тяжести сечения в плоскостях симметрии % и у; показатель степени к, при а_п = 0,161 < 0,4, определяется по формуле [46]:

к = ³ , ⁴⁴ - ^0,023^ (0,4 —   ) ² ₊ к = 2,02,

0,254+as             nV       0     ' ’ к = °275+^£ = 1,407.

⁰     0,16 + ^ 5

Для дальнейших расчетов к = 1,6 [46].

Зафиксировав угол приложения нагрузки q величиной а = 88 ° и решая уравнение (10) относительно q, предварительно подставив в него вычисленные ранее значения и (9), получаем значение равномерно распределенной нагрузки при l = 4,2 м, q = 45,82 кН/м. Разрушающая нагрузка на угловую колонну 1-го этажа составляет F 0 = ql = 192,5 кН.

Взрыв происходит в точке O на расстоянии C ₁ = 30 м от ЦТ 1-го этажа каркаса (рис. 3). Амплитудная составляющая вектора нагрузки имеет вид:

F 0 = [ F x 1 , F y 1 , F x 2 , F y 2 , F x 3 , F y 3 , M 1 , 0, 0] ^Т , где F x 1 = F 0 ⋅ cos α , F x 2 = F x 3 = ¹ ₂ F 0 ⋅ cos β ,

F y 1 = F 0 ⋅ sin α , F y 2 = F y 3 = ¹ ₂ F 0 ⋅ sin β ,

M 1 = F 0 ⋅ ( a 1 ⋅ sin α – b 1 ⋅ cos α ).

Проведен анализ колебаний базовой модели (БМ) каркаса и его поврежденных моделей для двух вариантов разрушения колонн 1-го этажа: угловой колонны А (ПМ–1) и рядом стоящей колонны В (ПМ-2) (см. рис. 3) при действии нагрузки F ₀ = 193 кН. На рис. 4 приведены осциллограммы перемещений центров тяжести перекрытий первого этажа БМ (черный цвет), ПМ-1 (красный цвет) и ПМ-2 (синий цвет) вдоль оси y .

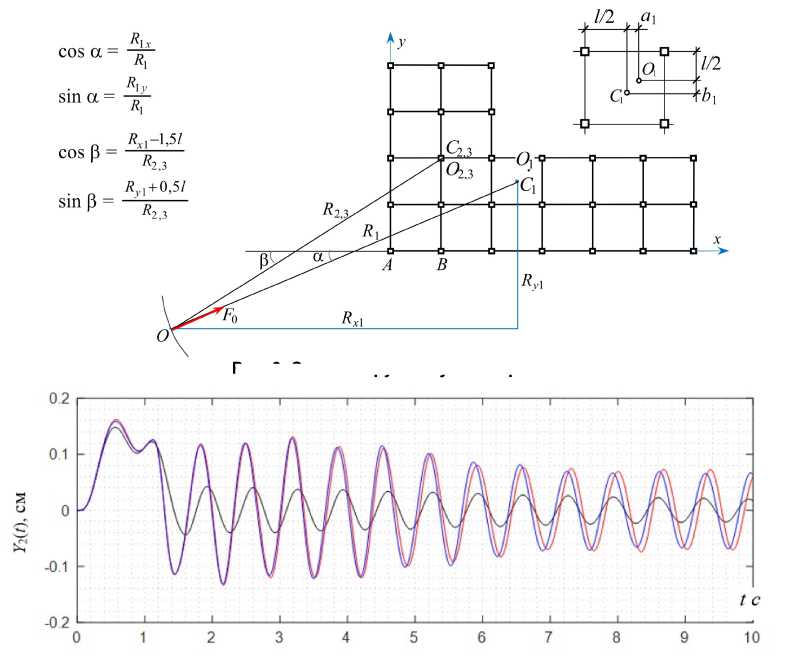
Рис. 3. Схема нагрузок в узлах каркаса

Рис. 4. Осциллограмма перемещений центров тяжести 1-го этажа вдоль оси y

Для осциллограммы ускорений ЦТ перекрытий 1-го этажа (рис. 5а, б) при t = t 1 показан скачок в момент внезапного разрушения колонны при t 1 = 0,75 t a = 1,125 c. Величина скачка согласуется с теоретическим результатом [41]:

A Y ( t 1 ) = 13,421 см/с ² .

На рис. 6а в расчетных моделях каркаса БМ, ПМ-1 и ПМ-2 изображены пространственные графики поверхностей нормальных напряжений, осредненных по сечению напряжений в наиболее нагруженной колонне каркаса. Поверхности построены в зависимости от изменения параметров нагрузки: угла наклона α амплитудной составляющей F0 к горизонтали и длины импульса ta. При построении графиков учитывались напряжения от статических нагрузок. На плоских графиках (рис. 6б, в) представлены ортогональные проекции нормальных напряжений при максимальном значении σz.

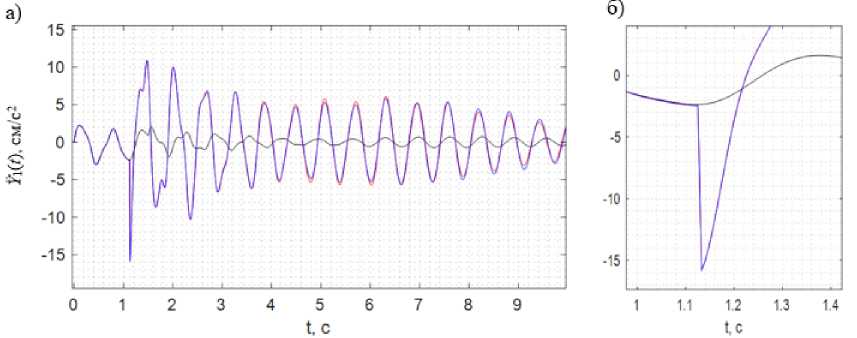
Рис. 5: а – осциллограмма ускорений центров тяжести 1-го этажа вдоль оси х ; б – фрагмент: скачок в момент разрушения угловой колонны при t = t 1

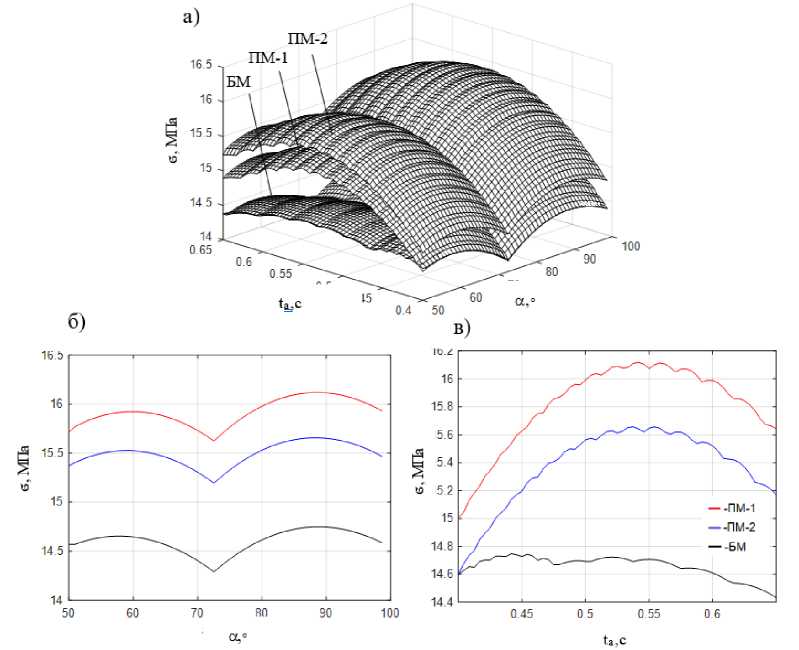
Рис. 6: а – поверхности максимальных нормальных напряжений в наиболее нагруженной колонне 3-этажного железобетонного каркаса; б – нормальное сечение по точке с наибольшими напряжениями по углу действия нагрузки; в – нормальное сечение по точке с наибольшими напряжениями по времени действия нагрузки

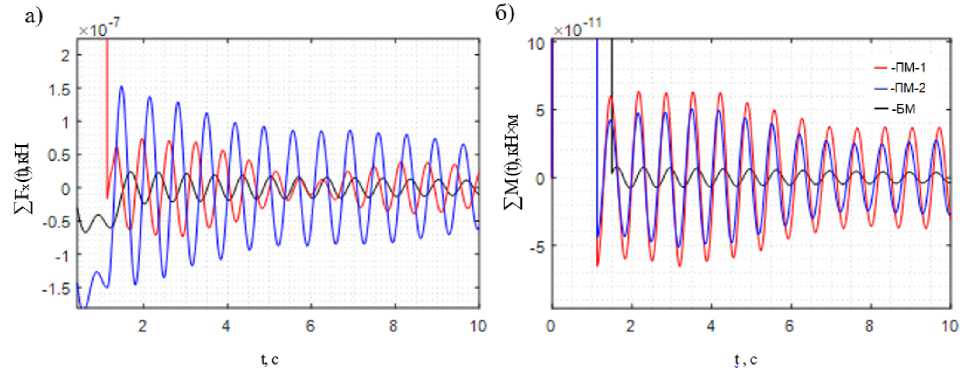
Рис. 7: а – осциллограмма суммарных сил, действующих в центре тяжести перекрытия 1-го этажа; б – осциллограмма суммарных моментов, действующих в центре тяжести перекрытия 1-го этажа

Заключение, выводы

Разработан аналитический метод расчёта дискретных диссипативных систем с выключающимися (разрушающимися) конструктивными элементами (или связями) от действия внешней нагрузки. В рамках теории временного анализа построены математические модели колебаний, позволяющие учитывать динамические параметры поврежденной системы до и после разрушения связи. В процессе движения РДМ конструкции, представляющей собой конструктивно нелинейную систему, в момент разрушения связи выполняется процедура замены «старых» динамических параметров модели на «новые». Одновременно с этим происходит смена начальных условий, обеспечивающая непрерывность колебательного процесса.

Численная реализация задачи для модели 3-этажного железобетонного каркаса, проведенная на отрезке времени t = 10 c, подтвердила высокую точность проводимого временного анализа (рис. 7). Невязка дифференциального уравнения движения (1) на интервале реагирования модели после повреждения не превышает величины ε ≤ 1,5 ^. 10 ^–7 кН.

Приведенные результаты анализа колебаний поврежденной модели каркаса, включая графики поверхностей максимальных напряжений, свидетельствуют о высокой эффективности метода. Открывается возможность детального изучения поведения строительных конструкций в экстремальных условиях отказа несущих элементов, а также возможность более углубленной разработки методов живучести конструкций и получения надежных оценок по повышению их сопротивляемости к разрушению.