Анализ кризиса на фондовом рынке Китая с помощью неоклассической модели потребительского спроса

Согласно классической модели Парето, совокупный спрос группы домашних хозяйств на некоторый набор из т товаров можно описать как результат принятия решения одним рациональным репрезентативным потребителем, который выбирает потребительскую корзину, максимизируя свою функцию полезности при бюджетном ограничении, т.е. решает задачу

F (Y ) ^ max , у g R ^

(р, Y) 6 0, где КД обозначает множество векторов из Rm с неотрицательными элементами.

Совокупный спрос группы домашних хозяйств может быть описан с помощью обратных функций спроса Р(X ), описывающих зависимости цен от совокупного потребления. Обратной задачей для модели Парето является задача построения функции F из некоторого класса Ф такой, что решением семейства задач

F(Y ) ^ max , у g R ™

(Р ( X ) , Y) 6 (Р ( X ) , X) ,

для каждого X являются функции спроса, обратные к которым совпадают с исходивши обративши функциями спроса Р (X).

Для того чтобы потребительское поведение группы домашних хозяйств можно было описать моделью Парето, обратные функции спроса должны удовлетворять некоторым условиям. Среди них есть условия существования интегрирующего множителя у дифференциальной формы обратных функций спроса

m

Е Р₃ (X)dX₃, (1) 3=1

известные как условия Фробениуса. Это условия типа равенства. Они могут нарушаться при малых возмущениях обратных функций спроса в норме пространства С ¹(Rm)-Возможность нарушения условий Фробениуса при таких возмущениях воспринималась экономистами как проблема интегрируемости [11].

В рамках теории выявленного предпочтения были разработаны критерии согласованности обратных функций спроса, которые могут быть применены к обратным функциям спроса, заданным в конечном числе точек. Данные о значениях обратных функций спроса в конечном числе точек представляются в виде конечного набора {(Р*, X^t)}'t=i тіеіі Р * іі (•оответствуюттщх ші объёмов потребления X*. Такой набор называется торговой статистикой.

Естественным обобщением модели Парето на случай двух и более репрезентативных потребителей является неоклассическая модель потребительского спроса, согласно которой функции совокупного спроса можно представить в виде суммы функций спроса двух и более рациональных репрезентативных потребителей, каждый из которых описывается моделью Парето.

Количество репрезентативных потребителей подлежит определению, однако при этом всегда стремятся описать потребительское поведение группы домашних хозяйств наименьшим количеством репрезентативных потребителей. Это количество зависит от свойств обратных функций спроса. В работах [13,14] отмечена связь между минимальным количеством репрезенетативных потребителей в неоклассической модели с положительнооднородными функциями полезности и классом дифференциальной формы обратных функций спроса.

Другим обобщением модели Парето на случай многих репрезентативных потребителей является модель временного диктатора, согласно которой в каждый период времени решение о совокупных объёмах потребления принимается одним репрезентативным потребителем, но в разные периоды времени это может быть разный потребитель.

Задачи проверки согласованности торговой статистики с неоклассической моделью и моделью временного диктатора оказываются NP-полными для некоторых классов функций полезности. Это означает, что для разработки эффективных численных методов анализа торговой статистики в рамках моделей с несколькими репрезентативными потребителями необходимо привлекать дополнительные модельные предположения, которые снимут проблему NP-полноты. Первым успешным примером такого подхода является анализ бюджетной статистики Великобритании [5], в рамках которого удалось проследить динамику формирования нового социального класса наиболее богатых домашних хозяйств, структура потребления которого сильно отличается от структуры потребления остальных домашних хозяйств.

Другим примером является анализ кризиса на фондовом рынке Китая летом 2015 года [9]. Для анализа был выбран период с января 2014 по август 2015. Было выдвинуто предположение, что кризис вызван действиями некоторых трейдеров в течение небольшого периода времени. В результате анализа удалось выделить одну акцию, торги которой приводят к слишком большому отклонению наблюдаемого поведения инвесторов от модели Парето.

Данная работа продолжает начатое в [9] исследование причин кризиса на фондовом рынке Китая в апреле 2015. Целью этой работы является доказателвство согласованности торговой статистики фондового рынка Китая в период с января 2014 по август 2015 с неоклассической моделвю потребительского спроса с двумя репрезентативными потребителями. Оставшаяся часть статьи организована следующим образом. В разделе 2 приводится описание основного инструмента анализа - обобщённого непараметрического метода. В разделе 3 приводятся описания в терминах торговой статистики двух обобщений модели Парето на случай многих репрезентативных потребителей - неоклассической модели и модели временного диктатора, - и приводятся оценки классов сложности задач проверки согласованности торговой статистики с этими моделями. В разделе 4 дано описание процедуры проверки согласованности торговой статистики фондового рынка Китая с неоклассической моделью. В разделе 5 приводится заключение.

2.    Обобщённый непараметрический метод

Говорят, что торговая статистика {(Р\ X^t)}t₌i рационализируема в классе Ф, если существует функция F из класса Ф такая, что для каждого t Е {1,...,Т} вектор X ^t является решением задачи

F(Y) ^ max , у +

⁽Р^t, Y ) 6 ⁽Р ^t, X^t) .

Введём класс функций Фң, состоящий из ненасыщаемых, монотонно не убывающих, вогнутых функций, которые непрерывны на R^, положительны на int R^ и являются положительно-однородными первой степени.

Теорема 1 (Африата-Вериана, [1,4,12]) . Следующие утверж-дения эквивалентны:

• 1)    Торговая статистика {(Р ^t,X ^t)}t=i рационализируема в классе Фң;

• 2)    Торговая статистика {(Р^t,X ^t)}^₌₁ удовлетворяет однородной сильной аксиоме выявленного предпочтения, т.е. для любых Ц,..., Ц выполнено

(Р^t1, X^t2 )⁽Р^t2, X^t3) ... (Р^tk, X^t1 ) >  (Р^t1, X^t1 )⁽Р^t2, X^t2) ... (Р^tk, X^tk ) .

• 3)    Существует положительное решение (A¹,..., A^T) системы линейных неравенств

A^t (Р^t,X^t) 6A^T (Р^Т,X^t), t,T = 1Т.                     (2)

Выполнение однородной сильной аксиомы выявленного предпочтения можно проверить за О(Т ³) операций с помощью алгоритма Варшалла-Флойда. На основе этого алгоритма можно найти одно из решений {A^t}^₌i системы (2), если эта система разрешима (см., например, [15]). По этому решению можно рассчитать индексы спроса F(X^t) и цен Q(Р^t) Конюса-Дивизиа (см. [3]):

Q(Р^t) = A,, F(X^t) = A^t (Р^t,X ^t) .                           (3)

Такой метод построения экономических индексов называется непараметрическим [4,7,14].

Если торговая статистика не удовлетворяет однородной сильной аксиоме, то она не согласуется с моделью Парето с функцией полезности из класса Фң и индексы Конюса-Дивизиа (3) не существуют. Для определения количественной меры несогласованности торговой статистики с моделью Парето в формулировку однородной сильной аксиомы вводится показатель ш.

Теорема 2 ( [7]) . Следующие утверждения эквивалентны:

• •    Торговая статистика {(Р\ X ^t)},L₁ ■удовлетворяет однородной сильной аксиоме выявленного предпочтения с показателем ш, т.е. для любых t1,... ,tk выполнено

ш^к ^р t1, X ^t2   j>^t2, X^t3 ) ... ⁽Р ^tk, X ^f) > ⁽Р^f, X' >⁽Р 2², X²² ) ... ⁽Р ^tk, X^tk ) .

• •    Существует положительное решение (А¹,..., Л^т) системы линейных неравенств

3.    Модели многих репрезентативных потребителей

л ⁴ (Р⁴,X^ 6шА^Т (Р^т,Х²), t,T = 1Т.                   (4)

Минимальное значение wmi_n показателя ш, при котором торговая статистика удовлетворяет однородной сильной аксиоме выявленного предпочтения, называется показателем нерациональности (в классе Фп)- Е ели ш_тіп = 1, то торговая статистика рационализируема в классе Фп и индексы Конюса-Дивизиа существуют.

Имея решение системы {ЛД^=і системы (4) при ш = wmi_n, можно построить индексы спроса и цен, используя формулы индексов Конюса-Дивизиа (3), даже при wmi_n > 1. Такой метод определения экономических индексов называется обобщённым непараметрическим методом [7,8].

С помощью однородной сильной аксиомы можно решать задачи прогнозирования объёмов потребления и цен. Пусть есть некоторая торговая статистика TS, удовлетворяющая однородной сильной аксиоме с показателем ш, и вектор цен Р, не входящий в торговую статистику TS. Тогда, в качестве множества К^п (Р ; TS, ш) прогнозов объёмов торгов при ценах Р можно рассмотреть множество всех таких X G Ry, что торговая статистика

TS и{(Р,Х)} удовлетворяет однородной сильной аксиоме выявленного предпочтения с показателем ш. Множество прогнозов цен при заданных объёмах потребления строится аналогично. В [2] показано, что множество Ку (Р;TS,ш') задаётся в виде системы линейных неравенств

К» (Р; TS, ш) = {X G R7 | 7т (Р, ш) (Рt, X) > (Р, X), T = IT}, причём коэффициенты ^т(Р,ш) могут быть определены за O(T3) операций с помощью алгоритма Варшалла-Флойда.

Краткое описание неоклассической модели приводится во введении. В терминах торговой статистики {(Р⁴,X ⁴)}*=1 задача проверки согласованности с неоклассической моделью с К репрезентативными потребителями сводится к проверке возможности представления каждого вектора X^t в виде суммы ^^і X ^k,t неотрицательных векторов X ^k,t такого, что торговые статистики

{(Р 4,x 1,4)}Т=і,..., {(Р V K,t)}= рационализируемы в некотором классе Ф.

В работе [10] доказано, что задача проверки согласованности торговой статистики с неоклассической моделью с двумя репрезентативными потребителями с функциями полезности из класса Ф^ является КР-полной. Класс Ф^ содержит функции, удовлетворяющие всем условиям принадлежности классу Фп, кроме условия положительной однородности. Вопрос об оценке класса сложности аналогичной задачи для класса Фп остаётся открытым.

Другим обобщением модели Парето на случай нескольких репрезентативных потребителей является модель временного диктатора. Говорят, что торговая статистика согласуется с моделью временного диктатора с К диктаторами с функциями полезности из класса, Ф. если сущссвл"тот функции Fi.....Ғк из к.тасса Ф такие, что каждьш вектор X* является решением задачи

Fk(У ) ^ max , ^{v 7} Y +'

(P*, У) 6

Задача проверки согласованности торговой статистики с моделвю временного диктатора с К >  2 диктаторам и является АР-по.тиой как для класса Фс (неопубликованная работа R. Deb¹), так и для класса Фн ( [6]).

4.    Анализ кризиса на фондовом рынке Китая

При анализе фондового рынка, как и в [9], все инвесторы разделяются на. две группы - основные инвесторы и высокочастотные трейдеры. Основные инвесторы воспринимают акции как услуги по росту дохода и редко меняют состав своего портфеля, посколвку рассчитывают не толвко на. рост стоимости акций, но на. выплату дивидендов. Их поведение при постоянных предпочтениях описывается моделвю Парето. Высокочастотные трейдеры стремятся заработатв на. высокочастотных колебаниях цен акций, поэтому они оченв часто меняют состав своего портфеля. Они разделяются на профессиональных и непрофессиональных трейдеров.

Поскольку в торговой статистике мы наблюдаем совокупные объёмы торгов, в которые входят торги как основных инвесторов, так и высокочастотных трейдеров, показатель нерациональности торговой статистики фондовых рынков, как правило, превосходит единицу, т.е. торговая статистика не согласуется с моделью Парето. Активность высокочастотных трейдеров зависит от акций, а. также от общего состояния финансового рынка. В периоды кризиса, активность высокочастотных трейдеров возрастает. Существует некоторое значение показателя нерациональности, характерное для нормального состояния фондового рынка. Это значение необходимо определить и считать, что если показатель нерациональности торговой статистики за. некоторый период не превосходит этого значения, то модель Парето является адекватным описанием поведения инвесторов за этот период.

В работе [9] для анализа, причин кризиса, на. фондовом рынке Китая использовался подход, состоящий из трёх шагов. На. первом шаге выбирается уровень логарифма показателя нерациональности П*, характерный для нормального режима функционирования фондового рынка. Китая. Этот уровень равен 0.035. Логарифм показателя нерациональности анализируемой торговой статистики, т.е. статистики с января 2014 по август 2015, равен 0.049.

На. втором шаге выделяются пары периодов, несогласованность которых приводит к росту логарифма показателя нерациональности сверх нормального уровня П*. Для этого рассматривается задача, линейного программирования т т

52 52 Ст* ^ min,

Т =1 t =1

Ст* > CTt — П* + ' — ДТ,                  t,T = 1,Т, и > о,                                t,T = 1Т.

Элементы ш*Т  решения этой задачи интерпретируются как показатели нерациональности пар периодов сверх допустимого уровня П*. Двойственной задачей

^екст работы доступен по URL: является задача о максимальном потоке т т

52 52 (^cTt - ^Q*)^Tt ^ max,

T =1 t =1

т

т

52 ^$Tt = 52^$ tT,

t =i

t =i

О 6 x_Tt

6 1,

т = ТД,               (6)

t,T = 1,7.                (7)

Среди решений этой задачи есть решение {x*_T}^T_T=₁ такое, что x*_T Е {0,1}. Это решение может быть представлено в виде ориентированного графа, в котором вершины соответствуют периодам, а рёбра соответствуют тем парам (t, т ), для которых х^ = 1.

Для анализируемой торговой статистики получается граф, представленный на рис. 1. На графе отсутствуют обозначения направлений рёбер, поскольку решение задачи (5) - (7) получилось симметричным, т.е. x*T = хД.

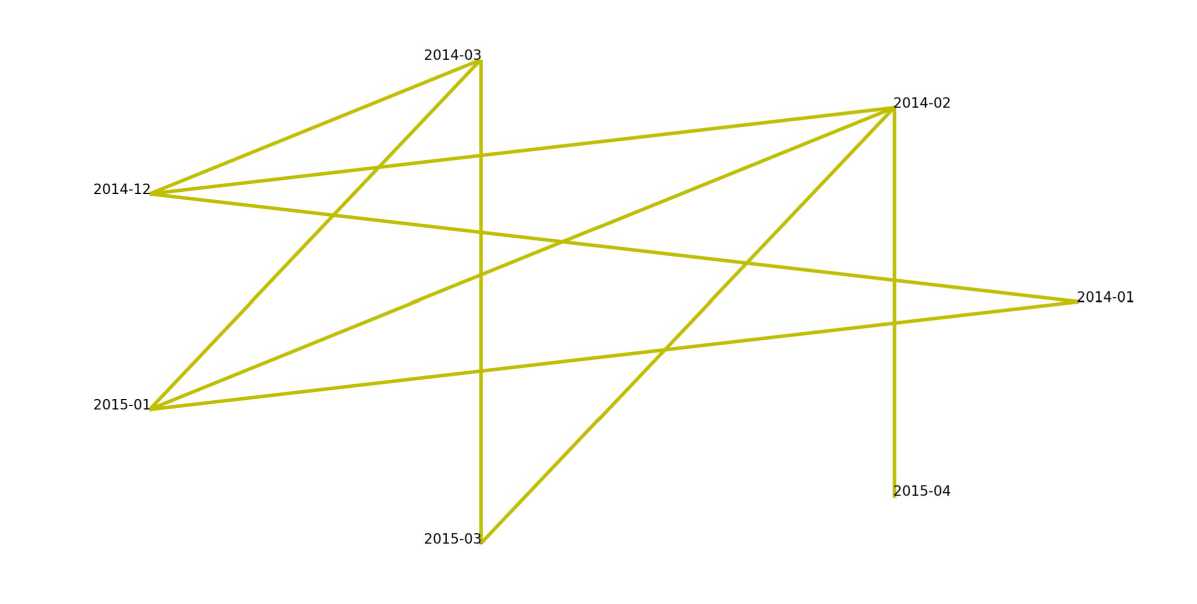
Рис. 1. Граф, построенный по решению задачи (5) - (7)

Граф оказывается двудольным. В первую долю входят три месяца 2014 года - январь, февраль и март. Во вторую долю входят 4 месяца - декабрь 2014, январь 2015, март 2015 и апрель 2015. Исключение любой из двух выделенных групп периодов приводит к снижению логарифма показателя нерациональности ниже нормального уровня Q*.

В [9] для дальнейшего анализа выбираются периоды второй доли. На третьем шаге решается задача выделения наименьшего количества акций таких, что корректировкой объёмов торгов только этих акций и только в выделенные четыре периода можно добиться снижения логарифма показателя нерациональности до нормального уровня Q*. В результате удалось выделить всего одну такую акцию. Это акция CITIC-Securities, ведущего инвестиционного банка Китая. Вернёмся ко второму шагу, на котором были выделены четыре периода. До этих периодов, т.е. с января по ноябрь 2014, торговая статистика рационализируема в классе Фн- После этих периодов, т.е. с мая по август 2015 торговая статистика также рационализируема. Было выдвинуто предположение, что некоторые профессиональные высокочастотные трейдеры спрогнозировали изменение предпочтений основных инвесторов и некоторое время вели себя так, как вели бы себя основные инвесторы после изменения предпочтений.

Это означает, что в течение некоторого временного интервала поведение инвесторов можно описать как взаимодействие двух репрезентативных потребителей с разными функциями полезности. Один репрезентативный потребитель соответствует основным инвесторам со старыми предпочтениями. Второй репрезентативный потребитель соответствует основным инвесторам с изменившимися предпочтениями.

Предполагается, что до выделенных периодов поведение инвесторов описывается моделью одного репрезентативного, который соответствует основным инвесторам со старыми предпочтениями, а после выделенных периодов поведение инвесторов описывается моделью репрезентативного потребителя, соответствующего основным инвесторам с новыми предпочтениями.

В интервале между декабрём 2014 и апрелем 2015, по-видимому, происходил некоторый переходный процесс, во время которого более адекватным модельным описанием является модель двух репрезентативных потребителей.

Для проверки этой гипотезы была поставлена задача для каждого периода с декабря 2014 по апрель 2015 представить объёмы торгов X * в виде суммы X * = X1,* + X2’* так, чтобы пару (Р*, X 1’*) можно было добавить к торговой статистике с января по ноябрь 2014, а пару (Р*,X2’*) можно было добавить к торговой статистике с мая по август 2015 так, чтобы логарифмы показателей нерациональности двух торговых статистик не превышали нормального уровня П*.

Для решения этой задачи рассмотрим следующую задачу. Пусть даны две торговые статистики TS main, TS aux, вектор объёмов торгов X * и соответствующий вектор цен Р *. Требуется найти проекцию X* вектора X* на множество прогнозов объёмов торгов Ку (Р*;TS main, e^Q*), построенное по торговой статистике TS main, так, чтобы остаток от проектпін X * — X * лежал в множестве прогнозов объёмов торгов Ку (Р *;TS^aux,eⁿ* ). построенном по торговой статистике TSaux.

Формально, задача ставится следующим образом:

ll^X* ^— Z ||² ^ шш, (8)

Z ЕК^(Р *;TS^main,e^Q*), (9)

X* — Z Е Ку(Р*;TS ^aux,e^Q*). (10)

Ограничения (9) - (10) линейные, поскольку множества Ку (Р *;TS^main₁e^* ) и Ку (Р * ;TS ^aux,e^Q ) задаются системами линейных неравенств, как было отмечено в разделе 2. Поэтому задача (8) - (10) является задачей кваратичного программирования с выпуклой целевой функцией. Для её решения разработаны эффективные численные методы. В данной работе использовалась реализация алгоритма решения задачи квадратичного программирования в библиотеке ALGLIB.

Задача (8) - (10) решает задачу о разбиении вектора объёмов торгов для одного периода. Для проверки гипотезы эта задача была решена для вектора объёмов торгов за декабрь 2014. При этом, поскольку предполагалось, что в начале переходного периода преобладали торги основных инвесторов со старыми предпочтениями, в качестве торговой статистики TSmain выступала торговая статистика за период с января по ноябрь 2014.

Получив решение Z^2014-12 задачи (8) - (10) для объёма торгов за декабрь 2014, я добавил пару (Р ^{2014 - 12} ,z ^2014-12) _к торговой статистике с января по ноябрь 2014, а. пару (Р ^2014-12,X^2014-12 — Z ^2014-12) к торговой статистике с мая по август 2015. Таким образом были получены две новые торговые статистики. Одна с января по декабрь 2014, вторая за декабрь 2014 и за период с мая по август 2015. Обозначим эти торговые статистики через TSleft’¹ и TS right’¹. По построению, логарифмы показателей нерациональности этих двух торговых статистик равны П*.

Далее, задача (8) - (10) решалась для объёмов торгов за январь 2015. При этом в качестве торговой статистики TSmain выступала статистика TSleft,1, а в качестве торговой статистики TSaux выступала статистика TSright’1. Эта задача имеет единственное решение Z2015 01. Пары

(р 2015 - 01 ^ 2015 - 01) _и (р 2015 - 01 _х 2015 - 01

—

jj 2015 - 01 )

были добавлены к торговым статистикам T S left ,¹ и T S right ,¹, в результате чего были получены статистики TS left ,² 1 і TS right ,².

Для оставшихся двух периодов - марта и апреля 2015 - были применены аналогичные действия. Отличие заключается только в том, что в качестве торговой статистики TS main выступала торговая статистика, содержащая периоды с мая по август 2015, поскольку предполагалось, что к концу переходного периода преобладали торги основных инвесторов с новыми предпочтениями.

В результате были получены две торговые статистики TS left ,⁴ и TS right ,⁴. Первая содержит периоды с января 2014 по апрель 2015, за вычетом февралая 2015. Вторая содержит периоды с декабря 2014 по август 2015, также за вычетом февраля 2015. Февраль 2015 не был выделен на этапе выбора периодов для дальнейшего анализа, поскольку он не приводит к росту логарифма показателя нерациональности сверх нормального уровня П*.

Объёмы торгов за февраль 2015 вместе с ценами за тот же период можно целиком добавить и к статистике TSleft,4 и к статистике TSright,4, при этом логарифмы показателей нерациональности останутся на уровне П*. Это также означает, что объём торгов за февраль 2015 можно разложить на сумму aX 2015-02,1 + (1 — а)х2015-02,2

для произвольного a Е [0,1], причём торговые статистики

TS

left , 4

U{(P ^2015-02 ,_аХ ^2015-02, 1

)}

И

TSright,4 и {(Р2015-02, (1 — a)X2015-02,2)} будут иметь логарифмы показателей нерациональности, равные П*.

Таким образом, удалось доказать согласованность анализируемой торговой статистики с неоклассической моделью с двумя репрезентативными потребителями в обобщённом смысле, т.е. с некоторым показателем нерациональности, который превосходит единицу. Первый репрезентативный потребитель соответствует основным инвесторам со старыми предпочтениями и существует с января 2014 по апрель 2015. Второй репрезентативный потребитель соответствует основным инвесторам с новыми предпочтениями и существует с декабря 2014 по август 2015. Это подтверждает выдвинутую ранее гипотезу о природе кризиса на фондовом рынке Китая.

5.    Заключение

В работе исследуется период кризиса на фондовом рынке Китая летом 2015 года в рамках неоклассической модели с двумя репрезентативными потребителями. Поскольку универсальных эффективных численных алгоритмов для такого анализа на данный момент не существует ввиду NP-полноты ряда задач, связанных с проверкой согласованности торговой статистки с моделью нескольких репрезентативных потребителей, необходимо привлекать дополнительные модельные предположения и эвристики. В случае с кризисом на фондовом рынке Китая в качестве такого предположения выступает гипотеза о том, что поведение инвесторов в докризисном и послекризисном периодах описывается моделью с одним репрезентативным потребителем, но с разными функциями полезности, а в кризисный период адекватной моделью является модель взаимодействия двух репрезентативных потребителей.

Это предположение привело к разработке эффективного эвристического алгоритма, который сводится к последователвному решению нескольких задач минимизации выпуклой квадратичной целевой функции при линейных ограничениях, т.е. задач выпуклого квадратичного программирования. Для решения таких задач существуют эффективные численные методы.

Таким образом, привлекая дополнительные модельные предположения и эвристики удалось провести анализ кризиса, преодолев связанные с VP-полнотой сложностные ограничения универсальных алгоритмов.

Работа выполнена при поддержке РНФ, проект № 16-11-10246.