Анализ квазипериодических и геометрооптических решений задачи фокусировки в продольный отрезок

Для получения оптического разряда в газе [1], в оптических системах звукозаписи и воспроизведения [2], для бесконтактных измерений в специализированных микроскопах [3] и многих других областях [4] требуются оптические элементы, фокусирующие лазерное излучение в продольный отрезок.

Для фокусировки излучения в продольный отрезок используются рассчитываемые в геометрооптическом приближении дифракционные оптические элементы (ДОЭ), известные как фокусаторы [4-6]. В работе [7] для расчета ДОЭ, фокусирующего в продольный отрезок, применен итеративный алгоритм. Основным недостатком методов [4-7] является неравномерность распределения энергии, сфокусированной в Е-окрестности оптической оси. В настоящей работе предлагаются аналитический и итерационный методы расчета новых "квазипериодических" ДОЭ, фокусирующих излучение в отрезок оптической оси. На основе вычислительного эксперимента проводится сравнительный анализ работоспособности геометрооптического и квазипериодического решений задачи фокусировки в продольный отрезок.

Постановка задачи фокусировки

Предположим, что лазерный пучок с комплексной амплитудой

W о ^{( r} ) = V I о ^{( r} ) ^exP ^[ i Р 0 ^{( r )]} ’ ^{r G}[ ^0, R ^] ’ ⁽¹⁾ где I 0 ( r ) - интенсивность, а p 0 ( r ) - фаза освещающего пучка, падает на ДОЭ с круглой апертурой радиуса R . ДОЭ располагается в плоскости z =0 (Рис.1) и преобразует падающее излучение в поле с комплексной амплитудой

W ( r ) = W о ( r ) exp [ i р ( r ) ] ,                     (2)

где p ( r ) - фазовая функция ДОЭ.

Требуется рассчитать фазовую функцию р ( r ) , обеспечивающую фокусировку падающего пучка в отрезок оптической оси с распределением интенсивности I ( z ), z G[ z 1 ,z₂ ].

Для удобства представим р ( r ) в форме

Р ⁽ r ) = р ( r ) — Р о ⁽ r ) .                          ⁽³⁾

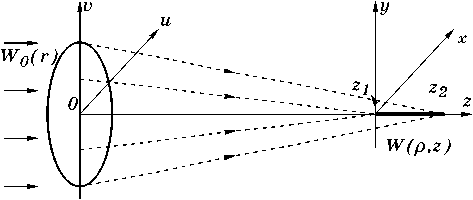
Рис. 1. Геометрия задачи фокусировки в продольный отрезок.

Представление (3) обеспечивает возможность расчета ДОЭ независимо от фазы р 0 ( r ) освещающего пучка. В дальнейшем изложении используется функция р(r ), которая однозначно определяет фазовое пропускание ДОЭ.

Расчет фазовой функции ДОЭ

Комплексная амплитуда W ( р, z ), р = ^x ²+ у² поля в фокальной области ДОЭ (см. Рис. 1) определяется через комплексное пропускание ДОЭ exp [ i р( r )] на основе интеграла Френеля-Кирхгофа [8,9]

k I. к р ² ] W ( р, z ) = exp l г ----lx z ] 2 z )

, (4)

где k=2n/2, 2 - длина волны, а J 0 ( r ) - функция Бесселя первого рода нулевого порядка [1о].

Для комплексной амплитуды поля на оптической оси (р=о) уравнение (4) принимает вид

R ._________ /..2 \

W (0,z) = - / TMr) expl ip(r) + ik — l rdr. (5) z о              \

Подстановка переменных в форме

^ = - И

r ² x = —

позволяет переписать уравнение (5) в виде

R Y                           XX к     2                                        (

W ( E ) =-- E J J I o (V2 x ) exp [ i ф, ( x ) ] exp - ik— dx , ⁽⁷⁾

z.    0                                         < где pt (x ) = p(V2x).

Как следует из формулы (7) задача фокусировки в продольный отрезок с распределением интенсивности I ( z ), z Е[ z 1 ,z₂ ], сводится к задаче расчета фазовой функции ф 1 ( x ) одномерного ДОЭ, фокусирующего пучок с комплексной амплитудой ^I ( Tz x ) exp ( - ik x ²/2 z , ) , x E [о, R ²/2], в поперечный отрезок с распределением интенсивности I ( — z ,/£ )/£ ² , ^ E [ —1, — z ,/ z ₂ ] в плоскости, расположенной на расстоянии z 1 от апертуры одномерного ДОЭ. Используя различные методы расчета фазовой функции ф 1 ( x ) одномерного ДОЭ можно получить различные решения задачи фокусировки в продольный отрезок.

В рамках геометрооптического приближения фазовую функцию одномерного ДОЭ можно найти из решения следующей системы уравнений [11,12]

В работе [16] сообщается о расчете "квазипе-риодических" ДОЭ, близких по своим функциональным свойствам к физическим голограммам, так как каждый период апертуры таких ДОЭ формирует полную фокальную область. При фокусировке сходящегося сферического пучка фазовая функция ф 1 ( x ), x Е [ x₀ , x 1 ], одномерного квазипериодического ДОЭ соответствует K-раз повторенной фазовой функции ф p ( x ), x Е[0,( x - x₀ )I К ], которая обеспечивает фокусировку в требуемый отрезок. Для каждого периодического повторения вводится свой постоянный фазовый сдвиг [15]

n i2

ф i = -^^, i = ^о,...^, К ^— 1, K

K - четное.

Таким образом, фазовая функция квазиперио-дического ДОЭ имеет вид

Ф 1 ^{( x} ) = ф ^{( x ) —} Ф о ^{( x} ) ⎨ ^{d ϕ( x )} = ^k ( ξ- x ) ⎪ dx f

I ^{0 ( x} ) = dL [ 1 1 ( 5 )    dx ’ x ^[

. X о , x

где ф 0 ( x ) - фазовая функция освещающего пучка, f -расстояние до плоскости фокусировки, I 0 ( x ) - интенсивность освещающего пучка, I 1 (£) - требуемое распределение интенсивности в плоскости фокусировки.

В частности, при фокусировке плоского пучка в продольный отрезок с постоянной интенсивностью уравнения (6) и (8) дают фазовую функцию ДОЭ в форме

ϕ ( r ) =

— kR ²

2 L

,    r2 L    л ln + 1

L R ^z 1

где L = z 2 - z i .

При LIz 1 <<1 использование аппроксимации In (1+ x )~ x - x² 12 приводит уравнение (9) к виду

ϕ ( r ) =

— kr²

kr ⁴ L

+

4 R ² z 2

Фазовая функция (10) соответствует фазовой функции тонкой линзы с введенной сферической аберрацией.

Следует заметить, что приближение геометрической оптики для расчета ф 1 ( x ) дает уравнения (9) и (10), которые совпадают с фазовыми функциями фокусаторов, описанных в работах [4-7]. В связи с этим в дальнейшем изложении ДОЭ, определяемые уравнениями (9) и (10), будем называть фокусато-рами.

Рассмотрим также получение фазовой функции ф 1 ( x ) на основе использования итерационного алгоритма Герчберга-Секстона [13] или одной из его модификаций [7,14,15], позволяющих улучшить геометрооптические решения (9) и (10).

ф 1 ( ^x ) = ф p

x - x

— a int

x — x 1

α

π

+—int

K

x

"i2

^{— x} 1

α

где a=( x₂ - x 1 )I К , а int[ x ] есть целая часть x .

Функция ф_p ( x ), x E[0,a], в уравнении (12) может быть получена аналитически на основе решения системы (8) или численно - используя итерационный алгоритм Герчберга-Секстона.

Используя функцию ф_p ( x ), полученную на основе решения системы (8), можно найти фазовую функцию ДОЭ, фокусирующего плоский пучок в продольный отрезок:

ϕ ( r ) =

— kR ² 2 KL

, [ LK ( ₂ R²

ln I---:---I Г --int

I R ² z 1 I К

r ² К

R ²

+ 1|+ф ( r ) (13)

где

^{ф( r} ) = К ^int

r ² К

R ²

Заметим, что для К =1 уравнение (13) соответствует фазовой функции фокусатора (9). Если L I z₁ <<1 уравнение (13) может быть сведено к виду

, х      kr ²      kR ² .

ф ( r ) =---1--int

’     2 z 1     2 z 1 К

₊ kLK

⁺ 4 R ² z 1²

r ²

-

r ² К

R ²

R int

K

+

r ² К

R ²

+ ф( r)

Для квазипериодического ДОЭ, определяемого уравнениями (13) или (15), фазовая функция ф _p ( x ) в уравнении (12) соответствует фокусировке в отрезок длиной N ( К) А, где А=2Л z₁K I R² - размер дифракционного пятна, а

N ( К ) = int

LR2

2 2 z 1 z ₂ К

Использование геометрооптического решения для ф _p ( x ) в уравнении (12) возможно только для N ( К) >>1 (т.е. для N ( К )=10 или больше), что налагает ограничения на возможные значения К . При

N ( K )=1-3 синтез квазипериодического ДОЭ становится невозможным даже с использованием итерационного расчета функции ф p ( x ) в уравнении (12).

Проанализируем уравнение (15). При ф ( r ) =0, фазовая функция (15) превращается в фазовую функцию многофокусной линзы [17,18] с количеством фокусов N , определяемым формулой (16). Координаты фокусов

R2

F=z i    1 R2 -2 i2 Kz, i = 0,1,... N

Таким образом, при ф ( r ) ^ 0 распределение интенсивности на оптической оси соответствует N пикам с шириной соседних пиков в K раз меньшим, чем расстояние между соседними фокусами. При K =1 пики сливаются, образуя отрезок вдоль оптической оси. Аналогичным образом дифракционная решетка обеспечивает разбиение фокального изображения на набор точек только при числе периодов K >1. Функция ф ( r ) в (13) соответствует введению сферической аберрации в (10) для фокусировки в отрезок ( F i , F_i+1 ). Это обеспечивает формирование непрерывного распределения интенсивности вдоль оптической оси при K >1.

Заметим, что проведенный анализ выполнен только для квазипериодических ДОЭ (13) или (15). Строгий вывод формы функции ~ ( r ) следует из формулы (7) и метода расчета квазипериодического ДОЭ [16], фокусирующего в поперечный отрезок.

Результаты численного моделирования

В этом разделе рассматривается численное исследование решений задачи фокусировки в продольный отрезок, полученных на основе геометрооптической функции (9) и квазипериодической функции (13).

Методы расчета ДОЭ, рассмотренные в предыдущем параграфе, направлены на создание требуемого распределения интенсивности на оптической оси и не управляют распределением в е-окрестности оптической оси, что намного важнее для практического использования ДОЭ. В этой связи, чтобы охарактеризовать работу ДОЭ, будем применять следующие характеристики: среднеквадратичное отклонение д полученного распределения от требуемого (СКО) и энергетическую эффективность E. Значение

^д( Е ) =i 7

^E ⎣ (

z 2— 2

—гJ(E (z,е)-E) dz z 1) z 1

___________I zz 2 -

где

_      1    z 2

E = ------- r J E ( z , s ) dz , E ( z , s ) = 2n J I ( r , z ) r dr

1z 2 - z 1) z10

характеризует среднеквадратичное отклонение осевого распределения энергии E ( z ,е) от среднего значения E ( е ) . Если е ^ 0, д ( Е ) характеризует среднеквадратичное отклонение распределения интенсивности на оптической оси от среднего значения. Величина E ( z ,е) характеризует энергию, приходящую в е -окрестность оптической оси с координатой z , в то время как значение

⎛ ^R

E ( е ) = E ( е ) 12п J I ₀ ( r ) rdr \ 0

характеризует среднюю долю энергии освещающего пучка, фокусируемую в поперечное сечение отрезка фокусировкиc радиусом е.

Левая часть таблицы 1 содержит рассчитанные значения E (е) и д(Е) [е=А, 2А и ЗА, где А = 0,61 • 2 ( z 1 + z ₂ )/( 2 R ) ] для фокусатора с фазовой функцией (9), предназначенного для фокусировки плоского пучка в продольный отрезок с постоянным распределением интенсивности со следующими параметрами: 2=0,63мкм; z 1 =320мм; z₂ =360мм; R =15мм. Средняя часть таблицы 1 содержит аналогичные значения для "квазипериодическо-го ДОЭ-1", а именно для ДОЭ с фазовой функцией (13) при K =2, 4. В правой части таблицы 1 расположены значения E (е) и д(Е) для "квазипериодического ДОЭ-2" при K =2,4, рассчитанного с использованием квазипериодической функции ф 1 ( x ) (12). В этом случае функция ф p ( x ) в (12) рассчитывалась с использованием адаптивной модификации алгоритма Герчберга-Секстона [7] с использованием в качестве начального приближения геометрооптической функции (9).

Таблица 1.

Энергетическая эффективность E(ε) и среднеквадратичное отклонение δ(ε) для фокусатора и для квазипериодических ДОЭ 1 и 2.

е	Фокусатор		Квазипериодический ДОЭ-1				Квазипериодический ДОЭ-2
			K=2		K=4		K=2		K=4
	δ(ε)%	Ε (ε)%	δ(ε)%	Ε (ε)%	δ(ε)%	Ε (ε)%	δ(ε)%	Ε (ε)%	δ(ε)%	Ε (ε)%
ε<<∆	29,1		31,0		35,3		12,5		11,1
∆	77,8	1,8	50,1	1,9	49,9	1,8	38,9	1,7	38,0	1,8
2∆	65,6	3,6	50,8	3,7	53,3	3,7	44,6	3,3	42,9	3,6
3∆	59,3	5,3	41,8	5,4	40,3	5,4	36,5	4,8	32,2	5,3

Анализ данных таблицы 1 показывает, что фо-кусатор (9) с осевой неравномерностью распределе- ния интенсивности в 29% имеет значительную неравномерность распределения энергии от 77% до

59% для s=A, 2A и ЗА соответственно. Для квази-периодического ДОЭ-1 неравномерность распределения интенсивности вдоль оптической оси больше и составляет 31% при K =2 и 35% при K =4. Большая неравномерность осевого распределения интенсивности для квазипериодического ДОЭ-1 обусловлена ростом погрешности геометрооптического решения (9) с увеличением K . В то же время неравномерность распределения энергии E ( z ,s) для квазиперио-дических ДОЭ в 1,4-1,6 раз меньше, чем для фоку-саторов. Для квазипериодических ДОЭ-2 по сравнению с квазипериодическими ДОЭ-1 неравномерность распределения интенсивности вдоль оптической оси примерно в три раза меньше при значительно меньшем (в 1,2-1,3 раза) снижении неравномерности распределения энергии E ( z ,s). Энергетическая эффективность E (s) приблизительно одинакова для всех исследованных оптических элементов и лежит в пределах от 1,7% до 1,9% при s=A и от 4,8% до 5,4% при s=3A.

На рисунках 2 - 4 приведены полутоновые распределения интенсивности I (р, z ) для фокусатора и квазипериодических ДОЭ 1 и 2 при K =4. Рис.2 демонстрирует значительное размывание поля в начале отрезка с энергией, в основном сконцентрированной в пределах фокального пятна шириной от 1,5A — 2A в начале отрезка до A в конце отрезка. Поля на рисунках 3 и 4 имеют периодическую структуру. Полученный результат соответствует анализу работы квазипериодического ДОЭ, приведенному выше (в предыдущем разделе).

При <р(r ) =0 ДОЭ-1 с фазовой функцией (13) соответствует многофокусной линзе (см. Рис. 5). Функция <р( r ) , уравнение (14), соответствует введению сферической аберрации и обеспечивает формирование структуры фокального поля близкой к структуре поля от фокусатора. Число периодов поля N обратно пропорционально K и определяется уравнением (16); при K =4 и исследуемых параметрах (Рис.2-5) N =16.

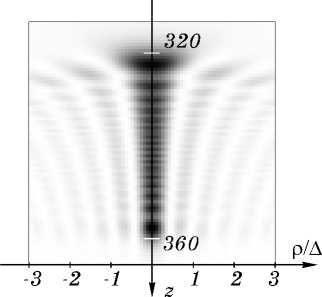
Рис. 2. Полутоновое распределение интенсивности в меридиональном сечении (p,z) фокальной плоскости фокусатора с параметрами: Я =0,63 мкм, z1 =320 мм; z2 =360мм; R=15mm.

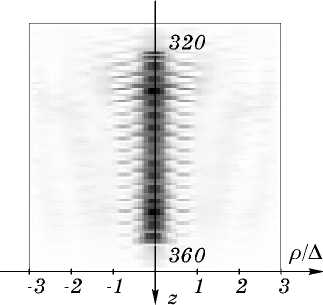
Рис.3. Полутоновое распределение интенсивности в меридиональном сечении (р,z) фокальной плоско сти квазипериодического ДОЭ-1 с параметрами: X =0,63 мкм, z1 =320мм; z2=360mm; R=15мм; K=4.

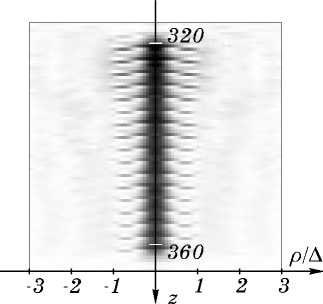
Рис. 4. Полутоновое распределение интенсивности в меридиональном сечении (р,z) фокальной плоскости квазипериодического ДОЭ-2 с параметрами: X =0,63 мкм, z =320mm; z₂ =360 мм; R =15мм; K =4.

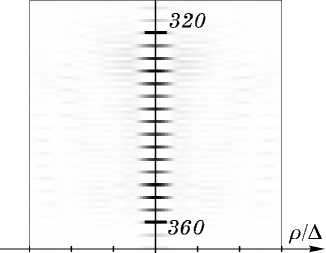
-3 -2 -1

Рис.5. Полутоновое распределение интенсивности в меридиональном сечении (р,z) фокальной плоскости квазипериодического ДОЭ-1 (Рис.3) при ф ( r ) = 0 в уравнении (13).

Таким образом, значение K влияет на структуру поля, формируемую квазипериодическими ДОЭ. В то же время погрешность геометрооптического и итерационного расчета функции ^ _p ( x ) в (12) увеличивается с ростом K . Из сказанного следует, что значение K можно рассматривать как дополнительный оптимизационный параметр расчета ДОЭ, обеспечивающий возможность оптимизации E (s) и d(s) при заданном s. Например, если s=2A, квазипериодический ДОЭ-1

обеспечивает более равномерное распределение энергии при K =2, чем при K =4. В то же время, если ε=3∆, квазипериодический ДОЭ-2 дает более высокую эффективность при K =4, чем при K =2.

Заключение

Получены и проанализированы квазипериоди-ческие решения задачи фокусировки в продольный отрезок. Квазипериодический ДОЭ может рассматриваться как набор концентрических колец, каждое из которых формирует весь отрезок фокусировки.

Численные исследования продемонстрировали лучшие показатели фокусировки для квазипериоди-ческих ДОЭ по сравнению с фокусаторами. Аналитически рассчитанный квазипериодический ДОЭ-1 обеспечивает формирование распределения энергии в ε-окрестности отрезка оптической оси, которое в 1,4 - 1,5 раза равномернее аналогичного распределения для фокусаторов. Квазипериодический ДОЭ-2, рассчитанный с использованием итерационного алгоритма Герчберга-Секстона, обеспечивает дополнительное уменьшение неравномерности распределения энергии E ( z ,ε) вдоль отрезка фокусировки в 1,2 - 1,3 раза по сравнению с ДОЭ-1.

Работа выполнена в рамках Государственной научно-технической программы "Наукоемкие технологии" при поддержке Министерства науки и технической политики РФ. Авторы выражают благодарность А.Е. Царегородцеву, С.И.Харитонову, Я.Е. Тахтарову и С.В. Смагину за помощь в подготовке настоящей статьи.