Анализ линейной спектральной смеси, инвариантный к атмосферным искажениям гиперспектральных изображений

Гиперспектральные изображения (ГСИ), получаемые космическими и авиационными средствами дистанционного зондирования Земли (ДЗЗ), несут в себе значительный объём информации о физико-химических свойствах объектов подстилающей поверхности и могут найти широкое применение при решении различных тематических задач.

При проведении спектрального анализа данных ДЗЗ для получения достоверного результата необходимо учитывать, что в отличие от лабораторных и полевых измерений и из-за пространственного разрешения видеоспектрометров практически все отсчеты космических и авиационных снимков оказываются смешанными, т.е. содержат в себе компоненты нескольких смежных объектов. Поэтому для идентификации исходных компонент и определения процентного состава смеси необходимо осуществлять моделирование процесса смешивания.

С другой стороны, атмосфера оказывает значительное влияние на регистрируемое отражённое излучение, что приводит к искажению регистрируемого сигнала. Обычно влияние атмосферы корректируется на этапе предобработки изображений с помощью процедуры атмосферной коррекции. Атмосферная коррекция опирается на априорную информацию о количественном и качественном составе атмосферы, включающем в себя распределение газов и аэрозолей в момент наблюдения. Поскольку непосредственное измерение параметров атмосферы для каждого изображения практически осуществить крайне трудоёмко, были разработаны некоторые модели атмосферной коррекции для излучения в опти- ческом диапазоне [1–3]. Эти модели были реализованы в ряде коммерческих пакетов, таких как MODTRAN, FLAASH, ATCOR и т.д. Однако на практике при обработке данных ДЗЗ часто возникает ситуация отсутствия необходимых исходных данных, например, метеорологических параметров и параметров съёмки (дальность видимости, азимут Солнца и т.п.). Такая ситуация существенно осложняет процесс анализа ГСИ ДЗЗ, в частности, для новых космических аппаратов группировки Ресурс-П [4].

В настоящей работе предлагается новый метод оценки параметров линейной спектральной смеси для ГСИ, позволяющий полностью исключить предварительную процедуру коррекции атмосферных искажений зарегистрированного изображения. Предлагаемый метод не требует использования специальных пакетов атмосферной коррекции и может быть применен непосредственно к искаженным гиперспектральным и/или мультиспектральным изображениям.

Статья организована следующим образом. В первом параграфе мы приводим обзор существующих методов решения задачи анализа линейной спектральной смеси для ГСИ. Во втором разделе мы даем описание предлагаемой агрегированной модели, включающей как указанную в первом параграфе модель линейной спектральной смеси, так и математическую модель атмосферных искажений, широко используемую для построения процедур коррекции этих искажений. Дается неформальная (вербальная) формулировка задачи оценки ее параметров . Дополнительно мы указываем частные случаи этой модели, связанные с ее возможными упрощениями. В тре- тьем параграфе мы предлагаем как формальные критерии оценки параметров модели, так и алгоритмы получения этих оценок (вообще говоря, различные). В четвёртом параграфе мы приводим результаты экспериментальных исследований по оценке эффективности предлагаемого решения. И в заключении содержатся полученные выводы и перспективы дальнейшей работы.

• 1.    Обзор существующих методов анализа линейной спектральной смеси

Существует два основных подхода к моделированию спектральных смесей. Первый подход – линейная модель спектральной смеси (Linear Spectral Mixture Model (LSMM)) [5]. Данная модель предполагает, что каждый пиксель ГСИ представляет собой линейную комбинацию спектральных сигнатур, соответствующих спектрам определённых материалов. Вторая скрытая спектральная модель (Intimate Spectral Model) предполагает, что значение пикселя формируется как нелинейная комбинация спектральных сигнатур. Эта модель может быть линеаризована, и затем для ее оценки могут быть применены методы линейного спектрального анализа (Linear Spectral Analysis (LSMA)).

Подробная классификация методов LSMA дана C.I. Chang в его монографии [5]. Согласно этой классификации все методы могут быть подразделены по характеру используемой априорной информации на две группы: управляемые (Supervised LSMA (SLSMA)) и неуправляемые (Unsupervised LSMA (ULSMA)). Для управляемых методов набор сигнатур, составляющих спектральную смесь, полагается известным, например, используются сигнатуры некоторой спектральной библиотеки. Для ULSMA характерно получение оценки неизвестного набора сигнатур спектральной смеси по изображению и затем применение к полученному набору управляемых методов разделения спектральных смесей. Другими важными параметрами алгоритмов LSMA являются используемый для разделения спектральной смеси оптимизационный критерий (квадратичный или иной) и вид ограничений, налагаемых на коэффициенты модели [6, 7].

Среди широко используемых подходов разделения линейной спектральной смеси следует особенно выделить нестатистические методы с квадратичным критерием оптимизации. Основное различие этих методов заключается в постановке задачи LSMA, а именно в ограничениях, накладываемых на коэффициенты линейной спектральной смеси. Полная система ограничений на коэффициенты спектральной смеси включает в себя [7]:

• 1)    требование неотрицательности коэффициентов смеси;

• 2)    требование нормировки коэффициентов, т.е. сумма коэффициентов должна быть равна единице.

• 2.    Агрегированная математическая модель и её частные случаи

Выделяют несколько групп методов LSMA. Первая группа методов решает задачу разделения спектральной смеси без использования ограничений. Например, метод проекции на ортогональное подпространство (Orthogonal Subspace Projection – OSP) и классификатор по методу наименьших квадратов (Least Square Projection Classifier – LSPC) [5]. Вторая группа включает в себя алгоритмы, использующие для коэффициентов одно из условий 1 или 2, и соответствует методам SCLS (Sum-To-One Constrained Linear Square) и NCLS (Nonnegativity Constrained Linear Square) [6]. Третья группа использует полную систему ограничений и называется FCLS (Fully Constrained Linear Square) [7].

Приведенные выше требования 1 и 2 дают возможность интерпретировать коэффициенты смеси как относительные концентрации материалов, соответствующих сигнатурам, которые участвуют в формировании смеси. Однако совместное использование этих требований приводит к вычислительно более сложной задаче, чем в альтернативных ситуациях.

Предлагаемый в данной работе подход использует указанную модель LSMM с полными ограничениями совместно с математической моделью атмосферных искажений MODTRAN, также хорошо известной и принятой в обработке данных ДЗЗ. В рамках такой агрегированной нелинейной модели оценки коэффициентов спектральной смеси, как оказывается, также могут быть получены как решение соответствующей задачи. При этом одновременно с оценкой коэффициентов линейной спектральной смеси в случае необходимости могут быть получены и оценки атмосферных искажений.

Модель линейной спектральной смеси с полными ограничениями описывает конкретный отсчет v ( n ) = ( v ₀( n ), ..., v J - 1 ( n )) T ( n = 0, N - 1) ГСИ как линейную комбинацию набора спектральных сигнатур { s } L =o :

L - 1 L - 1

v ( n ) = £ a I ( n ) s . , a I ( n ) - °, ^ a l ( n ) = 1, (1) l = 0 l = 0

где s l = ( s l0 ,s l 1 ,...,s l ₍ J - 1) ) T - конкретная сигнатура, J -число спектральных компонент изображения, a i ( n ) -коэффициенты модели для n -го отсчета ГСИ (для упрощения изложения будем использовать одномерную нотацию).

Известная математическая модель MODTRAN атмосферных искажений определяет спектральную плотность энергетической яркости (СПЭЯ) на регистрирующем датчике (на верхней границе атмосферы) для ламбертовой поверхности следующим образом [8]:

L = A: . B ^p ₊ c , 1 -p S 1 -p s

где p - коэффициент отражения подстилающей поверхности в проекции данного отсчета изображения на Земле, р - усреднённый коэффициент отражения для окрестности этого отсчета, величина S – спектральное альбедо атмосферы, величина С - яркость дымки; А и В - коэффициенты, зависящие от состояния атмосфе- ры и геометрических параметров съёмки и не завися

щие от свойств подстилающей поверхности

В использованных в (1) обозначениях выражение для СПЭЯ j -й компоненты n -го пикселя изображения будет иметь вид:

xj (n) =

A j v j ^{( n} ) + B j v j ^{( n} ) + C ¹ - v j ( n ) S j ¹ - v j ( n ) S j    j

где "P j ( n ) - среднее значение неискажённых отсчетов

ГСИ V j ( n + m ), m = - M , M , попадающих в окрестность радиуса M отсчёта с номером n .

Уравнение (3) формально позволяет выделить четыре частных случая, соответствующих следующим упрощенным моделям (далее модели 1-4):

• -    модель 1: S j = B j = Q = 0;

• -    модель 2: S j = B j = 0 и V) j ( n ) = const ;

• -    модель 3: S j = 0;

• -    модель 4: модель (3) в общем случае.

3. Формальная разрешимость: условия

Задача разделения линейной спектральной смеси при наличии атмосферных искажений заключается в восстановлении/оценке неизвестных коэффициентов спектральной смеси a i ( n ), i = 0, L - 1, n = 0, N - 1 и неизвестных коэффициентов атмосферной коррекции A j , B j , C j , S j в рамках выбранной модели (1-4). Коэффициенты смеси должны удовлетворять ограничениям неотрицательности и нормировки (1), а исходный набор сигнатур полагается известным.

Необходимые условия теоретической разрешимости данной задачи для каждой из указанных моделей могут быть легко получены путем прямого сравнения числа неизвестных и уравнений-равенств в выражениях (1) и (3). В результате имеем следующее условие разрешимости задачи:

N (J +1)> KJ + NL,

где слева от неравенства стоит число уравнений, а справа - число неизвестных параметров модели с номером K .

В данном параграфе мы приводим формальные постановки рассматриваемой задачи разделения линейной спектральной смеси и указываем алгоритмы получения решения для всех рассмотренных моделей. Отметим заранее, что в силу специфики формальной постановки для модели 1 формальная задача может быть сформулирована как стандартная задача квадратичного программирования, что позволяет использовать известные и, как следствие, вычислительно эффективные методы ее решения. Остальные три модели такое упрощение не допускают, что в конечном итоге приводит к необходимости использования итерационных методов нахождения решения, в частности градиентного метода оптимизации.

Модель 1: критерий и решение

Для получения формальной постановки задачи введем нормализованные значения отсчетов ГСИ

y j ( n ) = x j ( n )/ 5c j , где j) j - среднее значение j -й компоненты отсчета:

1 N - 1

x j = _VE x j ^{( n} ) .

N n = 0

Тогда из выражений (1) и (3) получаем следующую систему отношений:

' N -1 L -1                                   __________ __________

ЕЕ a i ( m ) • z mn = 0, n = 0, N - 1, j = 0, J - 1, m = 0 l = 0                                                         (4)

|E a i (n )=1,a i (n )> 0,

1 1 = 0

где использовано обозначение

(V N ) sj- y j ( n ) ,

mn

z lj

= <

j

( n

V

)

^{- 1}

m ^ n, l = 0, L -1, j = 0, J -1. m = n,

В силу наличия шумов, возникающих при регистрации ГСИ, а также из-за конечности представления вещественных чисел в ПЭВМ равенства в (4) на практике выполняются приближенно, что делает систему (4) несовместной. Тогда оказывается целесообразным заменить задачу (4) на оптимизационную задачу следующего вида:

<

| ЕЕ ^a i ( ^m ) • ^zj I ^ min, I ) a, m) V mi 7 ⁱ v I

Е ai (n ) = 1, ai (n )> 0, l

которая является стандартной задачей квадратичного программирования [9] и может быть решена эффективными узкоспециализированными алгоритмами.

Модели 2-4: критерий и решение

Решение задачи оценки коэффициентов спектральной смеси для оставшихся моделей может быть найдено в результате минимизации квадратичного отклонения пикселей j j ( n ) наблюдаемого изображения и пикселей 5с j ( n ), реконструированных с помощью уравнений (3) и (1):

N - 1 J - 1                          2

е2 = V V (x (n)- 5с, (n)) ^ min . (6) jV JV        cAC , в s (njJ n = 0 j = 0                                              I j ’ j ’ j ’ j ’ iV Дп=0,N-1

i = 0, L - 1

Для решения этой задачи мы предлагаем использовать градиентный метод [9], поскольку рассмотренный для первой модели подход здесь оказывается неприменим. В общем случае предлагаемый градиентный алгоритм имеет типовую структуру и может быть представлен следующим образом:

• 1.    Инициализировать значения неизвестных коэффициентов a i ( n ), A j , B j , Q , S j .

• 2.    На каждой итерации:

• (а)    вычислить значения производных критерия (6) по оцениваемым параметрам модели;

• (б)    скорректировать оценки параметров, используя основное соотношение градиентного метода:

• /а    де ²    , — ;    ———7

аi (n ) ——а i (n ) + ^-----—г, l — 0, L — 1, n — 0, N — 1, даl (n)

Q j — Q j +^^x , Q j — А -l B j\ C l S j ;j — o, J —i;

• ^д Q j

• (в)    проверить выполнение условий неотрицательности и нормировки для коэффициентов а i ( n ) из (1) и при необходимости скорректировать значения этих коэффициентов, проецируя новое решение на область допустимых значений;

• (г)    вычислить текущие оценки x ˆ _j ( n ) и v ˆ _j ( n ) , используя выражение (1) и (3) соответственно;

• (д)    вычислить текущее значение критерия (6);

• (е)    проверить условие остановки алгоритма и при необходимости закончить итерации.

• 4. Экспериментальные исследования

Для каждого частного случая модели 2–4, описанного выше, алгоритм имеет один и тот же вид. Основные различия заключаются только в виде производных критерия. Параметр Т >0 определяет шаг на отдельной итерации (шаг алгоритма) и регулирует скорость сходимости и точность решения, его выбор определяется стандартными рекомендациями к такого рода процедурам [9].

Входные данные, цель и задачи исследования, показатели эффективности решений

Экспериментальные исследования были проведены в среде MATLAB для набора синтезированных ГСИ. Для решения задачи квадратичного программирования использовался реализованный в среде MathLab алгоритм interior-point-convex (функция quadprog). Для создания набора из N пикселей с J спектральными компонентами были использованы случайные спектральные сигнатуры и коэффициенты с равномерным распределением компонент в интервале (0,1). Все н еискаж ённые влиянием атмосферы отсчеты v ( n ) ( n — 0, N — 1) были синтезированы в соответствии с моделью линейной спектральной смеси (1). Количество неизвестных коэффициентов линейной спектральной смеси, как очевидно, составляло N × L .

Коэффициенты, описывающие параметры атмосферных искажений в каждом канале изображения, также были заданы случайным образом с равномерным законом распределения в интервале (0,1) для каждой из компонент, так что A j , B j , S j е [0,1], C j >  0, j = 0,…, J –1. Входные данные x ( n ) моделировались из величин v ( n ) в соответствии с одной из предложенных моделей 1–4, в экспериментах с шумом к отсчетам ГСИ x ( n ) добавлялся шум определенной мощности (см. ниже). В моделях 3 и 4 в качестве функции, отражающей пространственную взаимосвязь искажённых отсчётов, было использовано взвешенное среднее значение пикселей:

M

• ^v ( n ) ^— S p mj^{n +} m ) ,                    ⁽⁷⁾

m——M pm — (13), Vn, m — —1,0,1.

Чтобы оценить точность получаемого решения, были рассчитаны среднеквадратичная ошибка оценок коэффициентов е а и среднеквадратичная ошибка е Xi представления отсчетов наблюдаемого изображения с помощью полученных коэффициентов, а именно:

• 1    N—1 L—1

^еа^— A TlSS ( ^а l ( n ^{) — a} i l ( n ) ) ,

• V ^NL n — 0 l — 0

• 1    1 N—1 J —12

еXi— aiftSE(xj(n)—xj(n)),i— 1,2,3,(8)

NJ n — 0 j — 0

где i – номер модели, ˆ – найденное решение задачи спектрального разделения, x ( n ) – наблюдаемый пиксель, и x ˆ( n ) – пиксель, реконструированный с помощью оцененных параметров модели.

Количество отсчетов, использованных в эксперименте, выбиралось из соображений достаточной быстроты вычислений. Каждый эксперимент был произведен K раз, и все результаты иллюстрируют среднее значение выбранных мер качества работы алгоритмов (8). Для градиентных методов использовалось предопределенное число итераций – 100000, шаг алгоритма Т = 0,0001.

Целью экспериментов было подтверждение работоспособности предложенного метода и определение влияния на точность оценки коэффициентов спектральной смеси и пикселей наблюдаемого изображения (8) следующих факторов:

• -    аддитивного шума, искажающего наблюдаемые отсчеты;

• -    размера ГСИ N (объема исходных данных);

• -    степени переопределенности набора гиперспектральных сигнатур.

Ниже мы приводим полученные результаты экспериментальных исследований для модели 1 как единственной модели с отличным от остальных алгоритмом получения решения, а также для модели 2 как представителя, для которого используется градиентный алгоритм. Заметим, для моделей 3 и 4 полученные результаты имеют похожий на результаты модели 2 вид и для сокращения изложения далее опущены.

Результаты экспериментов: влияние шума

В экспериментах с шумом к наблюдаемым отсчетам ГСИ x ( n ) был аддитивно (в каждом канале) добавлен независимый белый Гауссов шум с заданным значением отношения сигнал/шум (Signal to Noise Ratio – SNR). Результаты оценки показателей эффективности (8) в зависимости от SNR показаны на рис. 1.

Из графиков видно, что предложенный метод обеспечивает высокое качество решений при SNR больше 15. Можно сказать, что описанные методы являются устойчивыми по отношению к шуму, при этом решение с использованием квадратичного программирования обеспечивает более высокую точность. Кроме того, еX2 продолжает уменьшаться даже в том случае, когда ошибка представления коэффициентов еа достига- ет стабильного значения. Данный эффект означает, что происходит увеличение точности восстановления коэффициентов модели атмосферы.

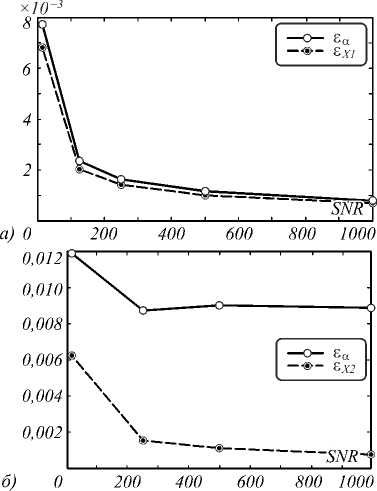
Рис. 1. Результаты экспериментов с шумом: а) модель 1 (J=100, L=10, K=5), б) модель 2 (J=50, L=10, K=5)

Результаты экспериментов: размеры ГСИ

На рис. 2 представлены результаты экспериментов с различным количеством отсчетов ГСИ. Данный эксперимент проводился при отсутствии шума. Видно, что в обоих случаях ошибка восстановления может быть рассмотрена как постоянная величина, так как имеет один и тот же порядок точности для всех значений объёма исходной выборки: для модели 1 обе ошибки имеют порядок 10^-14, для модели 2 ошибка ε α имеет порядок 10^-2 и ошибка ε X 2 имеет порядок 10^-5. Слабое изменение ошибки при увеличении объёма исходных данных означает возможность разделения исходных данных на несколько сравнительно небольших блоков, которые могут быть оценены независимо друг от друга, т.е. предложенные алгоритмы могут быть легко распараллелены.

Результаты экспериментов: влияние переопределён-ности набора гиперспектральных сигнатур

Для исследования влияния степени переопределён-ности набора сигнатур мы исследовали изменение точностных показателей (8) получаемых оценок в зависимости от числа «лишних» сигнатур, то есть сигнатур, которые фактически не участвовали в представлении (1) наблюдаемых отсчетов. Использованное число сигнатур в представлении (1), как и выше, далее обозначается символом L. Размер переопределённого списка сигнатур обозначается далее Lbig, причем Lbig≥L. В идеале, при решении коэффициенты «лишних» сигнатур должны оказаться равными нулю. Данный эксперимент показывает возможность использования полных или расширенных библиотек спектральных сигнатур для решения задачи разделения спектральных смесей ГСИ, то есть показывает возможность решения такой задачи даже тогда, когда полная информация о качественном составе сцены недоступна.

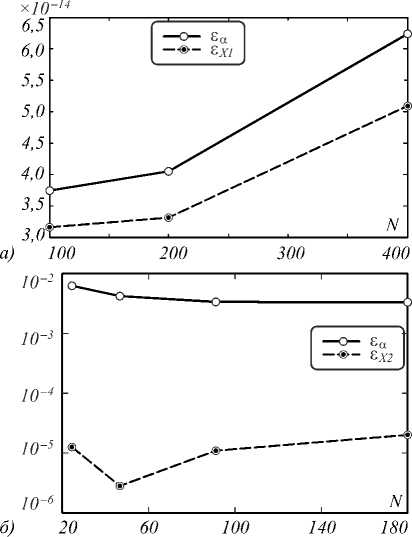
Рис. 2. Зависимость ошибки восстановления от объёма исходной выборки: а) модель 1 (J=100, L=10, K=5), б) модель 2 (J=50, L=10, K=5, по оси ординат используется логарифмическая шкала)

Результаты исследований приведены на рис. 3.

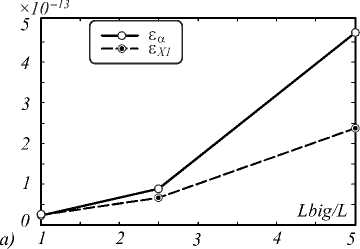
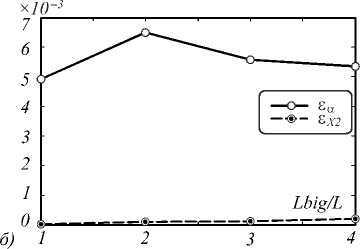
Рис. 3. Зависимость ошибки восстановления от степени переопределённости списка сигнатур: а) модель 1 (J=100, N=100, K=5), б) модель 2 (J=50, N=50, K=5)

Во всех экспериментах размер базового набора сигнатур составлял L=10. Можно заметить, что точ- ность реконструкции отсчетов ГСИ с помощью переопределённого набора сигнатур является практически постоянной величиной (незначительный рост ошибки можно объяснить ростом размерности задачи). Этот факт означает, что мы можем использовать переопределённый список сигнатур для решения задачи разделения спектральной смеси.

Заключение

В статье рассмотрена задача анализа линейной спектральной смеси, решаемая для атмосферно нескорректированных ГСИ ДЗЗ. Данное исследование имело целью показать принципиальную возможность получения решения задачи оценки параметров линейного спектрального разложения в ситуации, когда анализируемые ГСИ не подвергаются предварительным процедурам компенсации атмосферных искажений, использование которых на практике требует значительных априорных данных об условиях наблюдения (метереологических и др.).

В работе были рассмотрены различные варианты конкретизации модели наблюдения для случаев определения коэффициентов атмосферных искажений. Для них предложены алгоритмы оценки параметров моделей (коэффициентов линейной спектральной смеси и модели атмосферных искажений), использующие метод квадратичного программирования и градиентного спуска.

Экспериментальные исследования предложенного решения показали, что

• -    оно устойчиво к шумам на изображениях с отношением сигнал/шум больше 15;

• -    коэффициенты линейной спектральной смеси могут быть восстановлены по небольшим участкам исходных данных, независимо;

• -    существенного роста ошибки в зависимости от степени переопределенности набора спектральных сигнатур не наблюдается.

В целом предложенный метод и реализованные в его составе алгоритмы показывают как принципиальную возможность решения рассматриваемой задачи, так и высокие качественные показатели.

Вопрос эффективной вычислительной реализации предложенных процедур является объектом дальнейших исследований.

Работа выполнена при финансовой поддержке Российского научного фонда (РНФ), грант №14-3100014 «Создание лаборатории прорывных исследований дистанционного зондирования Земли».