Анализ маневрирования судна, снабженного двумя азиподами, с помощью его математической модели

*Мурманский государственный технический университет, г. Мурманск, Россия; ORCID: Х, e-mail:

Комплексное освоение Северного морского пути является составной частью национального проекта Российской Федерации, направленного на модернизацию и расширение магистральной инфраструктуры. Решение этой масштабной задачи невозможно без применения судов, способных работать круглогодично во льдах полярных широт. Для данных судов (различного назначения) характерны усиленные корпуса ледового класса и новые типы движителей – азиподы (винто-рулевые колонки). Их поворот вокруг вертикальной оси позволяет направить тяговое усилие в произвольном направлении и отказаться от руля, но при этом совершать более эффективные движения (например, движение кормой вперед). Особо эффективны движения судов с двумя азиподами. Для алгоритмизации расчетов, связанных с работой одного азипода, используются вычислительные схемы, например, схема А. Д. Гофмана (Гофман, 1988). Для систем с двумя азиподами приходится повторять эту схему дважды, выполняя ее для каждого азипода отдельно. Но даже такой способ позволяет учесть влияние одного азипода на другой за счет изменения условий обтекания второго азипода, если происходит поворот первого, и наоборот. В процессе расчетов определяются параметры потоков, обтекающих винт каждого азипода, с учетом координат (x, y) его расположения за корпусом. Моделирование работы двух азиподов усложняет графический интерфейс программы. Для каждого азипода создается джойстик, который позволяет управлять актуальной мощностью винта и поворотом азипода. Динамическое изменение этих параметров происходит согласно реальному темпу их изменения в судовой практике. Мощность переводится в уставные обороты винта, и далее они регулируются системой стабилизации оборотов. Поэтому к трем дифференциальным уравнениям плоского движения судовой модели (продольной, поперечной линейным скоростям, угловой скорости поворота судна) добавлены два дифференциальных уравнения вращения винтов в жидкой среде с учетом присоединенного момента инерции водных масс. С помощью такой модели исследуются также и системы стабилизации оборотов в переменных условиях маневрирования (например, в условиях циркуляции судна при действии ветра).

Целью настоящего исследования является определение параметров движения судна, оборудованного двумя азиподами, посредством моделирования процессов его маневрирования. Анализ испытаний математической модели позволяет установить влияние одного азипода на работу другого. Дальнейшие исследования по данной тематике предполагают создание набора базовых испытаний, которые в максимальной степени раскроют возможности работы судна с двумя азиподами в рамках функциональных задач, поставленных перед конкретными типами судов.

Материалы и методы

Исследование проводилось с использованием программного комплекса моделирования управления судном, снабженным двумя винто-рулевыми колонками (азиподами), выполненного авторами в двух программно-вычислительных средах (VB6 и MathCad) и зарегистрированного Федеральной службой по интеллектуальной собственности ¹ . Комплекс состоит из двух частей, первая из которых предоставляет удобный графический интерфейс, позволяющий для любого судна, корпусная модель которого уже рассчитана и расположена в базе данных, выбрать размеры акватории, начальное положение судна и запустить программу испытаний. Далее действия судоводителя состоят в управлении движителем посредством задания актуальной мощности, которая передается на винт каждого азипода, и поворота самих азиподов на произвольные углы по отношению к диаметральной плоскости (ДП) судна. Траектория судна при выбранных управлениях демонстрируется на поле акватории (рис. 1).

В динамическом режиме в текстовых полях отображаются в широком спектре значения характерных кинематических и силовых параметров маневрирования. Темп решения можно ускорять до 64 раз и замедлять до 8 раз. Однако слежение за параметрами маневрирования в процессе моделирования все же сложно – их слишком много, а смысл имеет лишь их комплекс. Поэтому все параметры пишут в массивы в каждом цикле моделирования (шаге интегрирования системы дифференциальных уравнений), что позволяет в конце процесса маневрирования вывести необходимые параметры из массивов в соответствующие файлы, которые затем читаются и анализируются во второй части программного комплекса. На основе такого группового анализа результатов делаются содержательные выводы. Графическая часть интерфейса представлена на рис. 1: блок управления азиподами (справа вверху) на фоне акватории, на которой показана траектория судна с изображением положения ДП судна через каждые 10 с интегрирования. В качестве последнего маневра выполнялась циркуляция по часовой стрелке, поэтому работал только азипод левого борта с актуальной мощностью 46,6 % от номинальной и углом его отклонения в 9° на правый борт. Азипод правого борта в это время практически не работал.

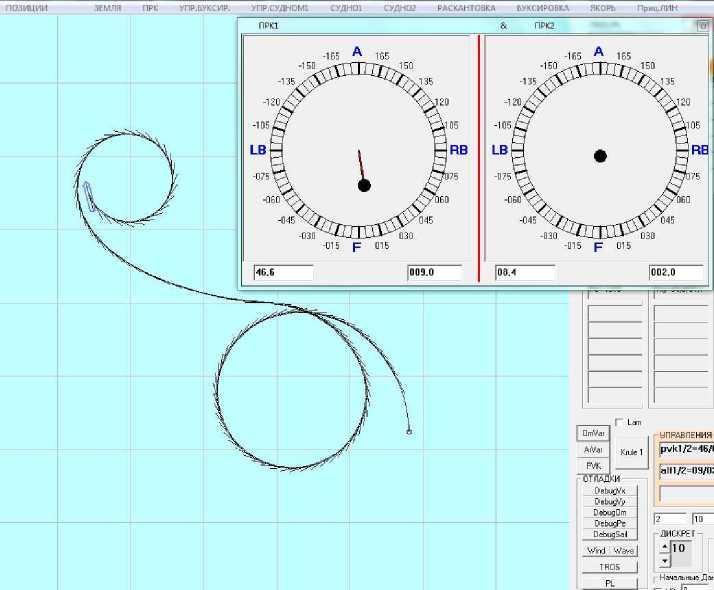
Рис. 1. Интерфейс системы управления судном (азиподы, траектория)

Fig. 1. The interface of the ship control system (azipods, trajectory)

Дифференциальные уравнения задачи моделирования управления судном

Задача описывается системой пяти дифференциальных уравнений первого порядка. Три первых уравнения описывают движения самого судна. В данном случае выбрана система в перемещениях, которая показана группой формул (Справочник по теории корабля, 1985):

( m ii ) [ d^ ] = - ( m 22 ) U y m + [       '   -2

+ C ax ^ a A T B v K - F rX + T e + F x ,

( m 22 ) [v ) = - ( m_u ) ■m-[2С ^в _р ^ + C 2

C^X3 — C^X0 -v + b- ² + 2b₂    ] PA L ^ +

2 ^x 1 ^{y 2} - 3       2

v _y v _y

- 16c 3

КАЛ i PA

6 v

- ]^p L ⁵-+ 2

_C P a A L v K _F

⁺ AY 2     ⁺ F rY ⁺ F Y ’

d m                                     ^- x ^- y           | ^- y | ^- y ^- x           2„ , , ,

(Jz66 )-T = -[2т1-х-y + m2--y + m3— 16m4----6---+ CM 0 L m I m I + dt                               v4             v6

+ C m _m (- 2 + L 2 m 2 ) sin(nfi) / n] ^^^L ^ + c am ^{P a} A VL Lv K + M r + M z •

В указанных формулах обозначения достаточно традиционны (Пашенцев, 2017). В данном случае существенны силовые воздействия от азиподов. Не меняя нотацию, усилия, обозначенные как рулевые нижним индексом r, будем относить к азиподу: F _rX , F _rY – продольная, поперечная силы; M _r – вращающий момент. При этом тягу винта T E исключим из первого уравнения, так как она автоматически войдет в силу F rX с учетом знака. Таким образом, три первых уравнения формально не претерпят значительных изменений, лишь иной смысл будут иметь рулевые усилия.

Два оставшихся уравнения представляют собой уравнения вращения винтов в водной среде; они по существу одинаковы структурно, но за счет управления могут иметь различные установочные значения мощности и оборотов. Первое уравнение представлено в теле подпрограммы на VB6, которая определяет приращение оборотов винта в переменных условиях хода. Дифференциальное уравнение выглядит следующим образом:

d^s = (ccc·Mdv – MyScrew.q) / JJ, где MyScrew.q – момент сопротивления винта в водной среде; JJ – момент инерции винта с учетом присоединенного момента инерции воды; Mdv – момент, развиваемый электродвигателем азипода:

Момент двигателя рассчитывается как пропорциональный квадрату оборотов винта с регулирующей аддитивной добавкой, пропорциональной разности уставных (MyUst.ns) и фактических (MyScrew.ns) оборотов. Такое обозначение параметров говорит о том, что в программном комплексе широко используется понятие объектов, которыми в данном случае является сам винт MyScrew и уставка работы движителя MyUst.

Дифференциальное уравнение работы винта второго азипода совершенно аналогично, но в нем фигурируют объекты MyScrew2 и MyUst2, поскольку каждый азипод может управляться независимо. Однако имеется также переключатель на синхронный или асинхронный режим управления.

Интегрирование системы уравнений

Дифференциальные уравнения решаются методом Эйлера. Опыт выполнения подобных задач с инерционными объектами (судно) показывает, что этот метод обеспечивает требуемую точность решения без необходимости обращаться к методу Рунге – Кутты. Результаты решения дифференциальных уравнений в виде приращений параметров движения просто добавляются к прежним значениям, например, продольная скорость Vx = Vx + dVx, обороты винта в секунду ns = ns + d^s и т. д. При этом в каждом цикле решения остальные переменные задачи вычисляются с учетом новых значений параметров движения.

Наиболее сложной проблемой является определение в таком цикле продольной, поперечной сил F _rX , F _rY и вращающего момента M _r каждого азипода. Для этого используем алгоритм А. Д. Гофмана (Гофман, 1988) с указанием введенных нами изменений:

– определяем относительную поступь винта азипода по формуле

J = (1 – wt)V/(ns·D), где D – диаметр винта азипода; wt – коэффициент попутного потока;

– рассчитываем коэффициенты упора k T и момента k Q винта с помощью универсальных кривых действия винта Ламмерена (van Lammeren et al., 1969; Pashentsev, 2018); в этом заключается основное изменение алгоритма А. Д. Гофмана, позволяющее определять упор и момент винта для любых условий эксплуатации;

– находим значения упора и момента для осевого натекания потока на лопасти винта:

T 0 = k _T p ^ns 2 ^D 4 , Q 0 = k Q p^ns 2 ^D⁵;

– вычисляем коэффициент нагрузки по упору для осевого натекания:

G t = (8k T )/(nJ 2 ).                                               (2)

Дальнейшие шаги алгоритма связаны с поворотом колонки азипода, вследствие чего изменяются условия обтекания лопастей, ведущие к изменению кинематических и силовых характеристик. Такой поворот в алгоритме А. Д. Гофмана учитывается с помощью диаграмм для коэффициента qR и угла 0 отклонения результирующего вектора силы азипода от его оси, приведенных на рис. 2 и 3 в виде функций угла V натекания потока на лопасти азипода в диапазоне 0—180 ° . Горизонтальная ось этих графиков разбита на 12 интервалов по 15 ° . Оба параметра зависят также от относительного шага винта P/D; выберем из них те кривые, которые описывают зависимости при P / D = 1.

Параметром выбранных кривых является коэффициент нагрузки по упору а Т , который вычислен на предыдущем шаге по формуле (2). Такой расчет с помощью диаграмм возможен только при проектировании судна с азиподом, когда решение выполняется небольшое число раз (в процессе подбора азипода). В нашем случае необходимо иметь аналитические выражения для qR и угла 0 , так как все расчеты повторяются многократно в каждом цикле решения. Поэтому кривые рис. 3 и 4 оцифрованы с использованием специальной программы комплекса и аппроксимированы в среде MathCad. Эти двумерные аппроксимации реализованы в виде двух подпрограмм (п/п) среды VB6, в которой выполнена часть комплекса, применяемая для маневренных испытаний.

Входом в п/п служат переменные st, psi, которые соответствуют параметрам OT и V, а выходами функций являются коэффициент qR и угол 0 (в VB6 не используются греческие буквы).

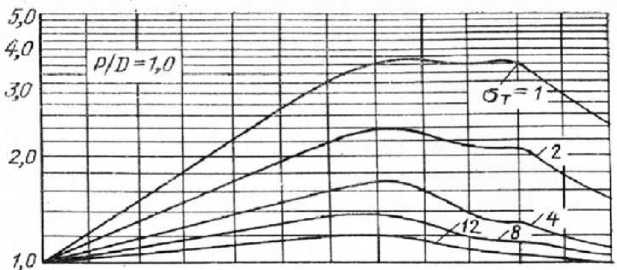
Рис. 2. Зависимость коэффициента qR от угла V , диапазон 0—180 ° ² Fig. 2. Dependence of the qR coefficient on the angle V , range 0—180 °

Рис. 3. Зависимость угла 0 от угла V , диапазон 0—180 ° 3 Fig. 3. Dependence of the angle 0 on the angle V , range 0—180 °

Для входа в эти функции следует определить угол натекания V, который находится как разность угла разворота азипода 5 и местного угла дрейфа Рм . Местный угол дрейфа без учета корпуса находится с помощью тангенса по формуле tg(P«) = (Vy - Xm®)/(Vx — Ум®), где xм и yм – координаты места расположения вертикальной оси азипода в системе координат, связанной с судном. Если азипод расположен в ДП судна, то yм = 0, но при двух азиподах их координаты yм нулю не равны и отличаются знаком. Угол Рм корректируется с помощью коэффициента х кинематического взаимодействия винта с корпусом:

Р м = ХР м .

Затем находится угол V = 5 — Р м* для входа в функции qRJrom_St_Psi и Teta_from_St_Psi.

Теперь можно определить величину результирующей силы R гребного винта

R = qR·T 0

и угол отклонения этой силы от ДП судна

• Y = 5 + 0 ,

что позволит найти продольную и поперечную силы, вызванные развернутым азиподом:

FrX = qR^T0cos(5 + 0)FrY = qR^T0sin(5 + 0), и учесть их в двух первых дифференциальных уравнениях группы (1). Добавим последний шаг нашего алгоритма – вычисление вращающего судно момента для третьего уравнения из группы формул (1):

M r = F rX y м + F rY x м .

Все шаги алгоритма выполняются для каждого азипода отдельно и в каждом цикле интегрирования дифференциальных уравнений. Параметры данного алгоритма (углы и силы) приведены на рис. 4, где показан развернутый на угол 5 азипод, расположенный в диаметральной плоскости судна: 5 — угол разворота азипода; V — угол натекания потока; 0 — угол отклонения силы R от оси азипода; у — угол отклонения силы R от ДП; ф — угол отклонения силы R от направления потока; Р м — местный угол дрейфа;

• ²    Гофман А. Д. Движительно-рулевой комплекс и маневрирование судна : справочник. Л. : Судостроение, 1988. С. 128.

• ³    Там же.

R – результируюшая сила на азиподе; X, Y – проекции силы R на ДП и перпендикулярно к ней; V _A – вектор натекающего потока.

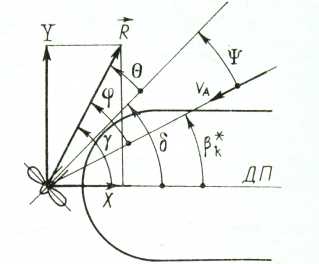
Рис. 4. Основные геометрические параметры расчетной схемы А. Д. Гофмана ⁴

Fig. 4. The main geometric parameters of the Gofman design scheme

Материалы, применяемые для решения задачи

После выполнения указанных шагов алгоритма программный комплекс готов к осуществлению любого вида маневрирования. Для этого используется управление маневрами с помощью графического интерфейса комплекса, показанного на рис. 5. В итоге маневрирования анализируются практически все параметры, которые изменялись при маневрировании. Двойным кликом на определенном текстовом поле главной формы маневров вызывается соответствующая подпрограмма, которая открывает файл и записывает в него определенный набор параметров. Так, клик на поле lblAzip при наличии азиподов записывает 16 параметров. Подпрограмма работает как для одного, так и для двух азиподов, и в этом случае пишет в файл парой строк следующие параметры, связанные с маневрированием:

• –    для первого азипода силы X, Y, момент М, углы δ и γ , процент загрузки мощности, скорости Vx и Vy, угловую скорость поворота ω , нагрузку винта по упору, угол θ , относительную поступь винта J, коэффициент qR, угол Ψ , обороты винта ^s;

• –    то же для второго азипода, но вместо Vx, Vy, ω пишутся координаты X, Y и курс судна K.

Рис. 5. Траектория судна при управлении двумя азиподами

Fig. 5. The trajectory of the vessel with two azipodes

• ⁴    Гофман А. Д. Движительно-рулевой комплекс и маневрирование судна : справочник. Л. : Судостроение, 1988. С. 131.

Рисунок представляет собой скриншот интерфейсной формы, с которой убран орган управления азиподами. Сложная траектория маневрирования сформирована постоянным разворотом второго азипода и изменением разворота первого азипода достаточно произвольно. Целью данных испытаний являлась демонстрация возможностей программного комплекса по получению параметров маневрирования с последующим их анализом, в частности, оценкой влияния перекладки одного азипода на работу другого.

Дальнейшие действия, связанные с анализом процесса маневрирования, проводятся в среде MathCad. Для этого файл, записанный в VB6, считывается в программе MathCad в виде матрицы с 16 столбцами и числом строк, вдвое превышающим число циклов интегрирования при решении уравнений (1). Этот этап анализа представлен в виде скриншота на рис. 6.

После считывания файла T20_grAzi2_8W.res в матрицу AZ идет разделение ее на векторы для различных параметров маневрирования. Испытания проведены с использованием модели танкера водоизмещением в 36 тыс. т, снабженного двумя азиподами (мощность каждого азипода 5400 кВт). Поперечные координаты осей азиподов y м составляют ± 12 м при диаметре лопастей 4 м.

Рис. 6. Чтение матрицы с результатами испытаний и разделение ее по параметрам маневрирования. Длительность испытаний Q = 3 557 с Fig. 6. Reading matrix with test results and dividing it by maneuvering parameters.

The test duration Q is equal to 3 557 sec

Результаты и обсуждение

Часть наиболее существенных результатов испытаний представлена в графической форме (рис. 7–9). Основная цель исследования – оценить влияние одного азипода на работу другого. Поэтому на рис. 7 вверху представлены изменения угла разворота азиподов в ходе испытаний. Второй азипод в течение двух длительных временных интервалов имеет постоянные положения, а первый азипод в этих интервалах разнообразно перекладывается; появляется возможность следить при этом за изменениями параметров второго азипода. Так, в нижней части рис. 7 показано, как изменяется коэффициен Qr1 при изменении угла разворота Alf1 азипода.

Из рисунка видно, что коэффициент Qr1, определяющий силы на развернутом азиподе, в значительной степени зависит от его перекладки. Коэффициент скачком изменяется при изменении угла кладки, что вполне естественно. Но на рис. 8 не обнаруживается существенной связи коэффициента Qr2 второго азипода с углом кладки первого. Такая связь очень слаба, она не является прямой, скорее, она косвенна, и происходит из-за изменения условий обтекания второго азипода при повороте судна. В то же время вращающие моменты азиподов изменяются почти согласованно при изменении угла разворота только первого азипода. Моменты значительно чувствительнее и изменяются почти одновременно скачком при развороте только одного азипода. Этот факт отражен на рис. 9, где приведены моменты М1 и М2 наряду с положением первого азипода (Alf1).

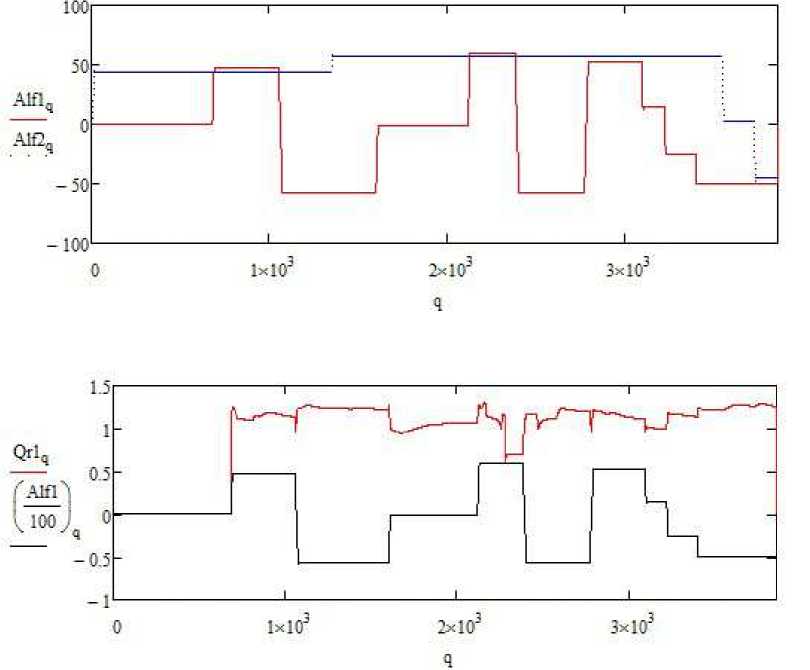
Рис. 7. Изменение перекладки азиподов в течение испытаний (вверху, ° ); изменение коэффициента Qr1 результирующей силы первого азипода в зависимости от его угла разворота (внизу)

Fig. 7. The change in the relaying of azipods during tests (top, ° ); the change in the coefficient Qr1 of the resulting force of the first azipod depending on its rotation angle (bottom)

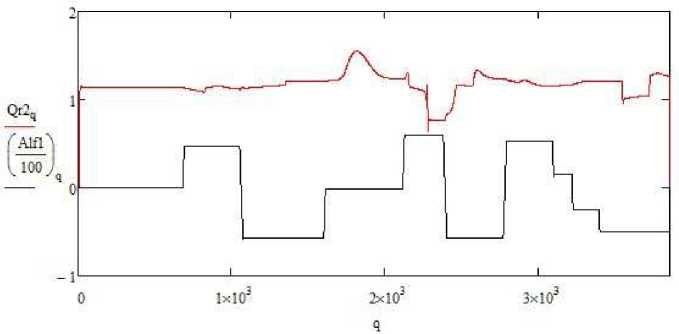
Рис. 8. Изменение коэффициента Qr2 результирующей силы второго азипода в зависимости от угла разворота первого азипода

Fig. 8. The change of the Qr2 coefficient of the resulting force of the second azipod depending on the angle of rotation of the first azipod

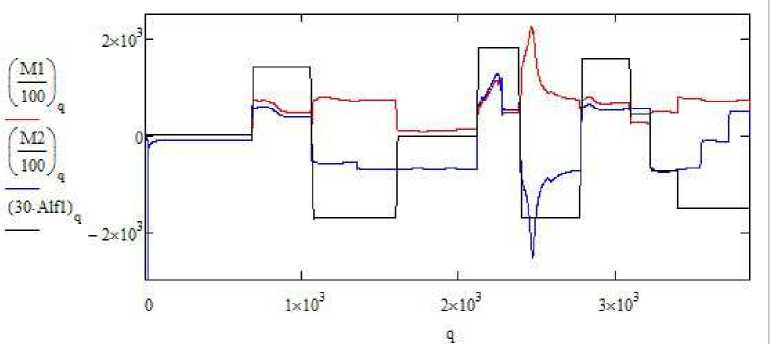
Рис. 9. Изменение вращающих моментов (кНм) первого и второго азиподов в зависимости от угла разворота первого азипода

Fig. 9. The change the torques (kNm) of the first and second azipods depending on the angle of rotation of the first azipod

Графические зависимости получены для всех параметров (кинематических и силовых), входящих в математическую модель, но не приведены здесь в силу ограниченности объема публикации. В полном объеме данные зависимости включены в отчетные материалы по тематике исследований ⁵ .

Выводы

Проведенные испытания модели и представленные в графической форме результаты позволяют сделать следующие выводы:

• 1.    Реализованная программно-математическая модель работоспособна, имеет удобный графический интерфейс для управления азиподами судна и фиксирует изменение любых параметров судовой модели во время процесса маневрирования.

• 2.    Интерфейс выполняет удобную отладку модели за счет введения специальных режимов управления, когда два азипода управляются независимо, синхронно и асинхронно, что дает возможность контролировать расчеты функционирования каждого азипода отдельно, а также их совместную работу.

• 3.    В ходе исследования установлено, что работа одного азипода влияет на работу другого через изменение параметров обтекающего потока. Каждый из них изменяется незначительно при развороте одного азипода, но совокупное изменение параметров существенно сказывается на силовых характеристиках другого азипода.

• 4.    В процессе штатных испытаний математической модели судна используются стандартные типы маневров (разгон, циркуляция, зигзаг), установленные ИМО (резолюция 137 от 5.12.2002). Для судов с двумя азиподами подобных стандартов пока не существует, следовательно, возникает необходимость создать набор базовых испытаний, которые в максимальной степени раскроют возможности работы судна с двумя азиподами в рамках функциональных задач, поставленных перед конкретными типами судов. Разумеется, в набор войдут упомянутые стандартные маневры, но появится большое число других маневров как следствие множества комбинаций разворотов и загрузок двух азиподов. Комплекс базовых испытаний будет формироваться и реализовываться в модельной форме в процессе дальнейших работ по данной тематике.

В настоящее время в силу объективных причин авторы не располагают данными натурных испытаний, с помощью которых можно оценить степень адекватности модели судовой практике, поэтому приглашают заинтересованных читателей данного материала к сотрудничеству для большей объективизации результатов.