Анализ методов бинарной классификации

признак, на основе которого происходит разбиение объектов, выбирается не из всех признаков, а только из случайно выбранных признаков (обычно m ). Выбор наилучшего признака осуществляется, как правило, с помощью энтропии либо с помощью индекса Джини.

Определение 1. Пусть имеется множество объектов О ={ O 1 … O n }, r из которых обладают некоторым свойством S , принимающим l различных значений. Тогда энтропия множества О по отношению к свойству S определяется по формуле:

l h ( о , 5) = -£ - log -.

i = 1 n      n

Чем меньше значение энтропии, тем больше информации содержится в варианте разделения и тем лучше разделение объектов.

Определение 2 . Для множества объектов О={O 1 …O n } и свойства S, принимающего l различ-ных значений индекс Джини вычисляя-ется следующим образом:

lO

Gini ( 0 , 5 ) = 1 -У .

t ! H I

Меньшее значение этого показателя также соответствует лучшему разделению объектов.

Таким образом, дерево строится до полного исчерпания подвыборки. Поскольку в данном методе используется набор деревьев решений, каждое из которых по-своему классифицирует объект, необходимо найти общее решение. Таким образом, прибегают к методу «голосования» или «усреднению». При использовании первого метода объекту приписывается тот класс, которому отдает предпочтение большинство деревьев из набора. В случае задачи регрессионного анализа прогнозируемое значение получается усреднением прогнозов по всем деревьям.

В качестве преимуществ данного метода можно отметить способность к обработке большего числа признаков и классов, нечувствительность к масштабированию, построению деревьев по данным с пропущенными значениями, а также одинаково хорошую обработку как непрерывных, так и дискретных признаков. К недостаткам можно отнести склонность к переобучению, то есть когда получается такой алгоритм, который слишком хорошо работает на примерах, участвовавших в обучении, но достаточно плохо работает на примерах, не участвовавших в обучении и большой размер получающихся моделей.

Градиентный бустинг деревьев решений. Термин « бустинг» от англ. «boosting» означает улучшение и представляет собой процедуру последовательного построения композиции алгоритмов машинного обучения, когда каждый следующий алгоритм стремится компенсировать недостатки композиции всех предыдущих алгоритмов. С точки зрения классификации бустинг деревьев решений считается одним из наиболее эффективных методов. Данный алгоритм строит модель в виде суммы деревьев:

M

f (x) = h о + v E hj(x)

j = 1

где h₀ - начальное приближение, v e (0,1] - параметр, регулирующий скорость обучения и влияя-ние отдельных деревьев на всю модель, h j (x) -деревья решений.

Новые слагаемые-деревья добавляются в сумму путем минимизации эмпирического риска, заданного некоторой функцией потерь:

L(y, y')=L(y, f(x))

Функция

L ⁽ у , у ‘ , у 2 ) = - E ⁽ у = k ) ln⁽ 2 ^SX)( y ^k ) )

^k = 1           E ^exp⁽ y k )

i = 1

предназначена для решения задач классификации на 2 класса.

Байесовский классификатор. В основе байесовского подхода лежит принцип максимального использования имеющейся априорной информации о процессах, ее непрерывного пересмотра и переоценки с учетом получаемых выборочных данных [1]. Применительно к задаче классификации используют так называемые байесовские сети. Строго байесовской сетью называется пара: N = G , Q где G - ориентированный ацикличный граф, а Q - набор условных распределений. Каждая вершина графа соответствует одной из переменных ( X [ . X m ), характеризующих исследуемый объект, для каждой из которых задано условное распределение:

Q x » х = P ( Х . 1 П х )

где П х . - множество непосредственных предшественников Xi в графе G .

Совместное распределение при этом определяется по формуле:

m

P ( Х „..., Х m ) = П P ( ^ i l П х . ) i = 1 .

Также байесовские сети позволяют оценить условные вероятности P ( XjXi ) остальных переменных. При классификации объектов на классы граф G условно разделяется на две части: вершина K , соответствующая классу объекта, и все остальные вершины. В случае наивного байесовского классификатора из вершины K проведены стрелки во все входные переменные X i . . X m , и других ребер у графа G нет (рис.1).

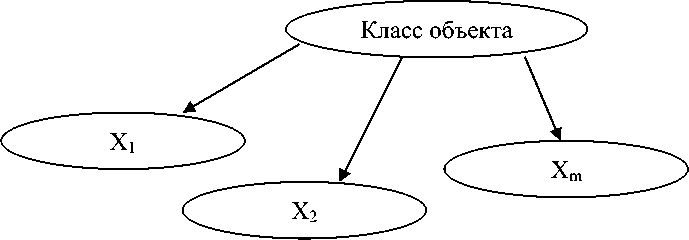
Рис. 1. Структура наивного байесовского классификатора

Обучение классификатора означает оценку условных вероятностей P(Xi\K), а классификация производится с помощью формулы Байеса:

P ( K = k ) П P ( X.= X i \K = k )

P ( K = k \ Х = X ) =---------- i = m-----------------

E P ( K = k ') П P ( X i = X i \ K = k ' ) k'                          1 = 1

Использование байесовских сетей позволяет избежать проблемы переучивания (overfitting), то есть избыточного усложнения модели, что является слабой стороной многих методов (например, деревьев решений и нейронных сетей). Также в модели определяются зависимости между всеми переменными, это позволяет легко обрабатывать ситуации, в которых значения некоторых переменных неизвестны. Однако перемножать условные вероятности корректно только тогда, когда все входные переменные действительно статистически независимы. Более того, невозможна непосредственная обработка непрерывных переменных - требуется их преобразование к интервальной шкале, чтобы атрибуты были дискретными

Дискриминантный анализ. Для определения вероятности принадлежности объекта к одному из двух классов используют линейные функции:

1,1 1

s1( x) = q о + q xi +... + qmxm

s 2( x) = q о + qt xi +...+qmxm , где q1^qm- параметры (веса) регрессии, которые находятся, как правило, с помощью метода наименьших квадратов, s(x) - «счет», который содержит достаточное количество информации для того, чтобы различать класс объекта. При этом выбирается тот класс, которому соответствует больший счет.

Логистическая регрессия. Пусть у определяет принадлежность объекта к классу и принимает значение 1, если объект принадлежит классу К 1 , и значение 0, если объект принадлежит классу К 2 . Тогда делается предположение о том, что вероятность наступления события у= 1, равна:

P{ у = 1| х} = f (z)

z = qTx = q 0 + q1 x +... + qmxm , где x - вектор-столбец независимых переменных xi„xm, q - вектор-столбец параметров (коэффициентов регрессии) q1^qm, fz) - логистическая функция (сигмоида, логит-функция):

f ( z ) =

1 + e -^z .

Так как у принимает лишь значения 0 и 1, то вероятность второго возможного значения равна:

P{ у = 0| х} = 1 - f (z) = 1 - f (qTx).

Таким образом, логистическая регрессия принимает следующий вид:

.   P { у = 1\ х }     f ( z )

log----------- =-------= q « + qx + —+ q„,x„, ■

P { у = 0\ x }  1 - f ( z )    ^{0   11        m m}

Для нахождения параметров q 1 ^q_m необходимо составить обучающую выборку, состоящую из наборов значений независимых переменных и соответствующих им значений зависимой переменной y . Формально, это множество пар:

( x ⁽¹⁾, у ⁽¹⁾),...,( x ^(m), y ^m))

где x ^{( 1} ) g R n - вектор значений независимых переменных, а y ^{( i} ) g {0,1} - соответствующее им значение у . Каждая такая пара называется обучающим примером.

Обычно используется метод максимального правдоподобия, согласно которому выбираются параметры q , максимизирующие значение функции правдоподобия на обучающей выборке. Максимизация функции правдоподобия эквивалентна максимизации её логарифма. Для максимизации этой функции может быть применён метод градиентного спуска или метод Ньютона-Рафсона [3]. Сама задача классификации решается следующим образом: объект x можно отнести к классу у= 1, если предсказанная моделью вероятность P { у = 110,5} >  0,5 , и к классу у= 0 в противном случае. Граничное значение может быть отлично от 0,5. Получающиеся при этом правила классификации являются линейными классификаторами.

Главным преимуществом логистической регрессии является учет ограничений на значения вероятности, которые не могут выходить за рамки 0 и 1, а также работа с входными данными любого рода, благодаря чему данная модель нашла свое применение при нахождении переходных вероятностей состояний системы [4] . К недостаткам следует отнести чувствительность к корреляции между факторами, поэтому в моделях недопустимо наличие сильно коррелированных независимых переменных.

Для оценки качества бинарной классификации прибегают в основном к методам ROC-анализа. ROC-кривая, также известная как кривая ошибок, отображает соотношение между долей верных положительных классификаций от общего числа положительных классификаций

(true positive rate) с долей ошибочных положительных классификаций от общего числа отрицательных классификаций (false positive rate) при варьировании порога решающего правила. Показатель AUC (площадь под ROC-кривой) дает количественную интерпретацию ROC-кривой. Считается, что чем выше показатель AUC, тем качественнее классификатор.

Для решения сформулированной задачи была использована среда программирования Python(x,y), представляющая собой набор библиотек и программного обеспечения для численных расчетов, анализа и визуализации данных на основе Python с готовой реализацией описанных выше моделей. Для сравнительного анализа результатов классификации была сформирована выборка, состоящая из 1000 объектов, каждый из которых характеризуется 20 признаками. Исходная выборка была разделена случайным образом на обучающую выборку (700 объектов) и на тестовую выборку (300 объектов). На рис. 2 изображены ROC-кривые моделей по данным контрольной выборки, а также показатель AUC для каждой модели.

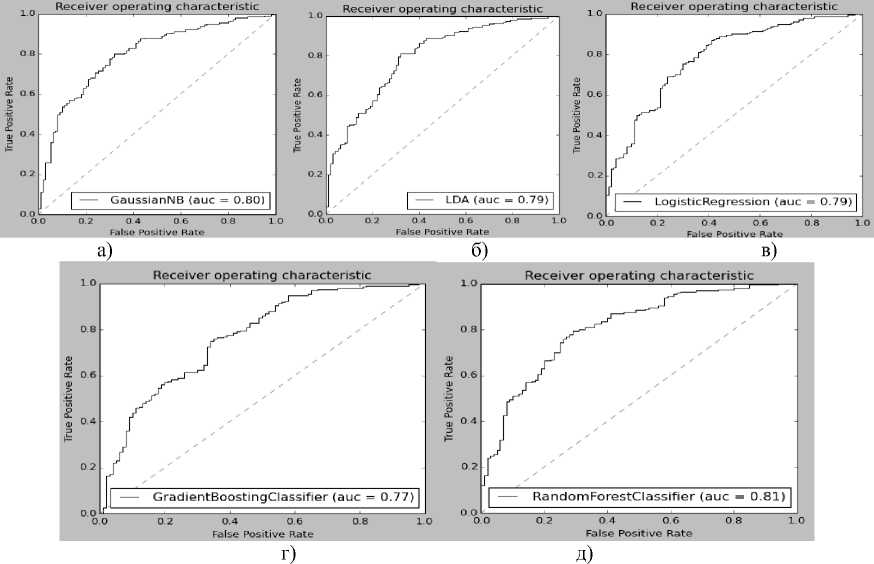
Рис. 2. ROC-кривые: а) байесовский классификатор, б) дискриминантный анализ, в) логистическая регрессия, г) градиентный бустинг, д) «случайный лес»

Результаты ROC-анализа, в том числе и показателя AUC показывают, что, на первый взгляд, расхождения моделей совершенно незначительны и сложно определить качество класс-сификации. Однако при представлении результа- тов классификации объектов в виде табл. 1, в которой отражено количество верно и ошибочно классифицируемых объектов, преимущество по точности классификации можно отдать методу дискриминантного анализа.

Таблица 1. Результаты классификации объектов различными моделями

Название модели	Верно классифицирова нные		Ошибочно классифициров анные
	кол-во (из 300)	%	кол-во (из 300)	%
«случайный лес»	207	69	93	31
градиентный бустинг деревьев решений	220	73,3	80	26,7
наивный байесовский классификатор	225	75	75	25
дискриминантный анализ	227	75,7	73	24,3
логистическая регрессия	222	74	78	26