Анализ методов определения проводимости изоляции для линии с отпайкой

Ш.Н. Хусаинов, Р.Р. Нараеваг. Челябинск, ЮУрГУ

Предложен выбор схемы замещения линии с изолированной нейтралью, имеющей одну отпайку, по анализу погрешности результатов расчета параметров изоляции, и проанализированы результаты расчета для случая ухудшения изоляции на одном из участков сети одной из фаз.

В данной работе определение параметров изоляции и места повреждения участка сети, имеющей одну отпайку, проводится в два этапа. На первом этапе выбирается схема замещения линии с отпайкой по анализу погрешностей результатов расчета параметров изоляции. Расчеты проводятся по методу узловых потенциалов (МУП) и методу контурных токов (МКТ). На втором этапе анализ выполняется для случая ухудшения изоляции на одном из участков сети.

Рассмотрим первый этап расчетов, в котором анализируется два варианта схемы замещения линии с отпайкой: П-образная и Т-образная, рассчитанные по методу узловых потенциалов и методу контурных токов.

При этом считается заданной трёхфазная цепь с симметричным источником ЭДС и симметричной нагрузкой, поэтому расчёты выполняются для схемы фазы А. Для сопоставления результатов расчета и погрешностей определения параметров изоляции по МКТ и МУП использована цифровая модель линии с отпайкой с П-образной и Т-образной схемами замещения, записанная в пакете Math-CAD. При решении задачи цифрового моделирования, как и в работе [1] заданными считаем следующие параметры:

• 1)    продольное комплексное сопротивление Z главной линии;

• 2)    продольное комплексное сопротивление Z₃ отпаечной линии;

• 3)    длина главной линии / и отпаечной линии /₃;

• 4)    относительная длина к первого (головного) участка главной линии;

(главная линия длиной / делится местом присоединения отпайки на две части; соответственно сопротивление первого участка линии 2^ = к • Z и сопротивление второго участка Z₂ = (1 - к) Z);

• 5)    коэффициент распределения проводимости т; (аналогично проводимость первого участка линии

• 5    = щ • К и проводимость второго участка линии К, = (1-т)-К);

• 6 ) напряжение в точке присоединения отпайки и₀;

• 1 ) нагрузка в конце главной и отпаечной линий Z_a2 и2_о3 соответственно.

Схемы замещения фазы участка сети цифровой модели представлены на рис. 1 (для П-образной) и на рис. 2 (для Т-образной). Расчеты выполняются по участкам сети, начиная со второго участка.

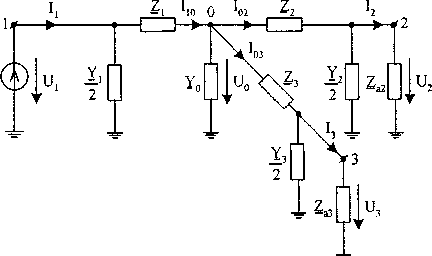
Рис. 1. П-образная схема замещения фазы участка сети

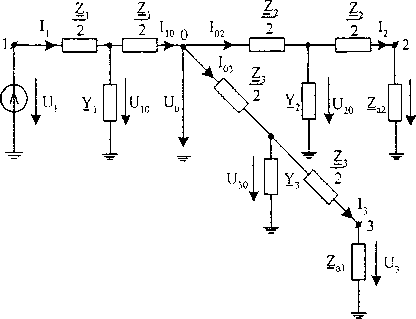
Рис. 2. Т-образная схема замещения фазы участка сети

Для П-образной схемы цифровой модели (рис. 1) определяем:

• -    сопротивления в конце второго участка вместе с проводимостью изоляции (2_]2) и в месте присоединения отпайки (2₀₂)

  ₂ . ² .

  -¹² Z^-K+2’

  
  

  —02 ^_ —2 +Z12 ;

  
  

• -    ток на втором участке от места присоединения отпайки (по закону Ома)

—02

• -    напряжение в конце второго участка ^2 ⁼ Л)2 ' —12 ;

• -    ток в конце второго участка

Аналогично выполняются расчеты для третьего участка сети с заменой индекса 2 на 3.

Для головного участка сети определяем:

• -    проводимость в месте присоединения от-паечной линии

У.+Ъ+Хз

2       ;

• -    ток через У_о в месте присоединения отпайки

i^U^.

• -    ток на первом участке от места присоединения отпайки (по I закону Кирхгофа)

Ло = Л)2 + /оз + /о ;

• -    напряжение в начале основной линии u,=i_to.z,₊u₀.

• -    ток в начале основной линии

л=л0+ц-|-

Для Т-образной схемы цифровой модели (рис. 2) определяем:

• -    сопротивления на последовательном , параллельном Z₂₂ участках цепи и в месте присоединения отпайки Z₀₂

2, £12 -у⁺ ^_а2;

z ~¹² •

• -²² z^-b+V

• —02 = у ⁺ Л₂2^:

• -    ток на втором участке от места присоединения отпайки (по закону Ома)

• -    ток в конце второго участка ^у2“²02 ₇  ’

—12

• -    напряжение в конце второго участка ^2 ⁼    ' Хи2 ■

Аналогичные расчеты для третьего участка сети с заменой индекса 2 на 3.

Для головного участка сети определяем:

• -    ток на первом участке от места присоединения отпайки (по I закону Кирхгофа)

Ло = 4г + 4з

• -    ток в начале основной линии

• •         ■ 2,

• Л = Ло +(Ло -у+^оЛЛ;

• - напряжение в начале основной линии 7     2

^=Л-у+Ло'у+^о.

Действительные значения измеряемых величин, полученные в цифровых моделях П-образной и Т-образной схем замещения, используются при моделировании измерений напряжений и токов приборами класса 0,1 для 100 циклов измерений. Расчеты выполняются по методу узловых потенциалов и методу контурных токов для обоих вариантов схем замещения: П-образной (рис. 3 (МУП); рис. 4 (МКТ)) и Т-образной (рис. 5 (МУП); рис. 6 (МКТ)).

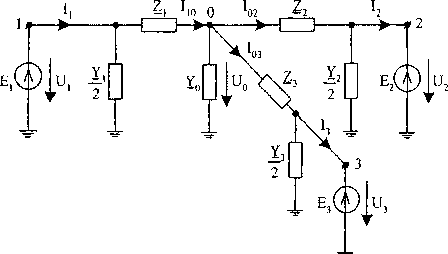
Рис. 3. П-образная схема замещения фазы участка сети для расчета по МУП

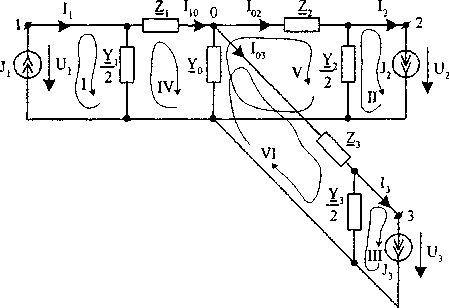
Рис. 4. П-образная схема замещения фазы участка сети для расчета по МКТ

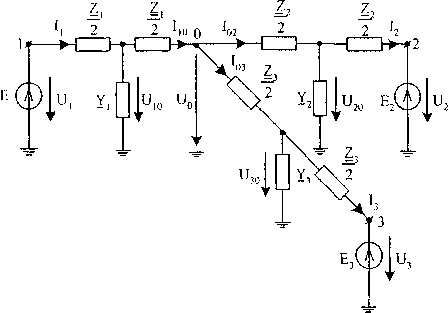
Рис. 5. Т-образная схема замещения фазы участка сети для расчета по МУП

С учетом коэффициента проводимости т и замены 111      _v 8+8

- + —- + — = g получим 8о =g + —— • 8 .^2 8

С учетом приведенных выше обозначений и, выразив токи через разность потенциалов по закону Ома, после преобразования получим уравнения: U_o -(g + ^^-l/,    -U₂-

°         2        1 Zj 2          Z2

,£7Wv)._L = 0

Z] 1    2      1

U2

+18 -8Re(v) •(i-m).l+

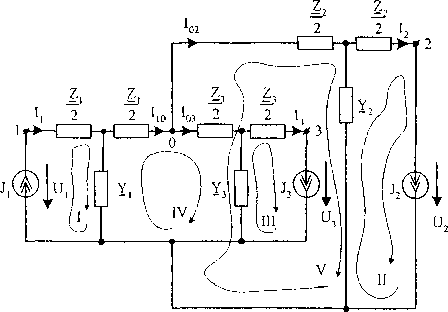
Рис. 6. Т-образная схема замещения фазы участка сети для расчета по МКТ

В расчетах принимаем U_; = U_X; U₂ = U₂ • l^jW'⁾; U₃ = U₃ • .^^Jm(v,), где V = ^2 + № •

Так же, как и в работе [2] вводятся обозначения: 1_Х = /, -Г^№ ;i₂=I₂- Г^№ ; 1₃=1₃-     .

Для первого варианта расчетов П-образной схемы замещения по МУП (рис. 3) данными цифровой модели являются:

• У , Уз ,m,U₀=U₀- i^⁰, у = у/₂ + jy₃.

Запишем уравнения по методу узловых потенциалов:

+12.фКе^ _ 0;

Г, cjlmW _У

—-------211+

Z3            3           2

и выполним расчет данных уравнений в пакете MathCad.

Для расчета П-образной схемы замещения по МКТ (рис. 4) данными цифровой модели являются: У, 8, т, i_w=i_w-t^, 1₀₂=1₀₂-^,

8з = 8з •8м''03,   = 4'2+74'3 ■

Запишем уравнения по методу контурных токов:

81 = 8;

82 = 1

• 8з = 8 =

81 ■ 841 + 82 ■ 842 + 8з ■ 843 + 84 ■ 844 +

+85 845 + 8б 846 = ^44 1

81 ■ 851 + 82 ■ 852 + 8з ■ 853 + 84 ■ 854 +

+85 ’ 855 + 8б ■ 8зб = ^55 >

81 ’8б1 +82 8б2 + 8з '8бз +84 '8б4 +

+85" 8б5 + 8б ■ 8бб = ^66 >

2      2

где Z4] = - — =     —, Z42 = 0 ; Z43 = 0 ,

8    m-Y

Ф\ =йг;

Ф2=и2,

Фз = ^L8

Фо 8)0 ~Ф\ ' 8и ~ Фз 'Хоз ™ Фз '8)3 ⁼ О'

где 81 = —;     8)2 ⁼ 77-;      & = —;

8)о ~--'---1--- ^ 8' здесь 8> ~ —*---*--

Z, Z2 8з                  2 2 2

2    1             2        2

Z₅₅ = Z^ + — + — = Z₂ +------+--

Y, У,       Y-m-Y Y +

Z56=Z65=-U-3_; Z61=0; Z62 = 0;

In / +b

2          „    2    1    _    2      :

-63         -66   -3            -3

A44 = 0 ; £₅₅ = 0 ; E₆₆ = 0 ; /₄₄ = Ao > As ~ A

Аб = Аз

02 ’

С учетом вышеизложенных обозначений и выразив напряжения U_x, U_D, й_г через контурные токи по закону Ома полученные уравнения преобразуются к виду:

2,

-+Ao -(Ai m-Y

2 m-Y

" Az '

Аз ’., „ “ 0;

-72 f7^1^- ■

+Az "(Аг +

Y-m-Y

Y-m-Y

• — Aor

Х + Хз

2        ■2

^г) + Аз-^г = 0;

_j . £jMwY 3_ _ j 2

• 3 Хз 10 Х+Хз ■            22

2      •2

u\-1\ —-+Ao —~ = °;

m-Y m-Y

^.^ReW^ f/Re(v).

Y-m-Y °2Y-m-Y

= 0;

U₃ .(М^ _+/з ,^Jm(_V) .JL-^ .L ₌ 0.

А Хз

Данные уравнения рассчитываем в пакете MathCad.

Для второго варианта расчетов Т-образной схемы замещения по МУП (рис. 5) данными цифровой модели являются:

Y,

m, U_Q=U₀-£^№, U_xo =U_xo-£^№'°,

A₂ = Аг ■ ^^мг , и_ю = U_m -£^J^ , _V = Х^ +_7W Запишем уравнения по методу узловых потенциалов:

Фо ' Ао “ Ф1'Ai “Фг 'Аг _Фз 'Аз = АоS

“Фо ’Ао +Ф1 'Ai “Фг 'Хз “Фз ’Аз ⁼ Ль

“Фо ’ Ао “ Ф1 ' Ai + Фг Аг “ Фз' Аз = Аз >

“Фо'Ао “Ф1 ’Ai “Фг 'Аг + Фз ’Аз = Аз>

2    2    22

где Ао =—+—+— = Ai =Ао = —,

—1 —2 ~3—1

Аг = Ао = ”; Аз = Ао = ™;

ХзХз

2   24

Ai="+—+6 =—+«-А; Аг=А1=0;

2   24

Аз=А1=0; Аг=—+— + Ь= — + Х-т-Х,

2    24

Фо = ^о; Ф1 = ^ю; Фг = Ао; Фз = Ао, Ао = о;

. _Ёх-2 _2-Ux _Er2 _2-U,

Z] z, z2 z2

• ■    _ £₃-2 _ 2-I/₃

733Z '

С учетом приведенных выше обозначений и, выразив токи через разность потенциалов по закону Ома, после преобразования получим уравнения:

• ■           •     2            22

А '^1 “А10 Ао Ао ~ = °;

Х\       ХзХз

• ■   2          42

• -А--+Ао-(- + « А)-А — = 0;

9         49

• -А-— + Ао-(—+Г-_т-У)-[/₂.А^к*).™ = О;

Хз       ХзХз

• ■      •     22

  /₁₊А--+Ао-у-Ао-«-А = О;

Х\Х\

• /₂ . ^Re(v) _ _Uq . 2- ₊ А₂₀ • 2_ + и₂₀ . Y - А₂₀ . т Y = 0;

  /₃-А^т«-п_{0   +}п₃₀ ■—+А_зо-^ =о.

Хз       Хз

Расчеты данных уравнений выполним в пакете MathCad.

Для расчета Т-образной схемы методом контурных токов (рис. 6) за исходные данные из цифровой модели примем:

• У, Ь,т, 1_ю=1_хо.^М_ю=1_т.^. Запишем уравнения по методу контурных токов

Ai = А;

Аг = A i

Аз = А;

Ai 'Ал! +Аг 'Z42 +Аз ’Адз +Ад 'А44 +

+Аз ■ А45 ⁼ Еда ;

Ai ’Ам + Аг 'Азг + Аз ’А53 + А4 ’Азл +

+Аз ’ Азз = Аз, где А41 = “тг = —-; А42 = °; Алз = “";

А ^т-Х             А

Хз 1

А45 “ Аз4 “⁵ⁱ ""О’

„ Z2   Z3   1    1   Z2   Z3 1       1

2  2  ^  ^  2  2   Y-m-Y ^

£44 = 0; £55 = о; Л4 = Ло; ^55 = ^02

С учетом приведенных выше обозначений и выразив напряжения Ux, U2, U3 через контурные токи по закону Ома полученные уравнения преобразуем к виду m-Y 3 К 1   2   2 m-Y К

-ЛоЧ^+^О;

2£3

j ^/Re(v)

2 " m-Y-Y

1             7      1

+ /(^1 + ±) +

3 К ° 2 К

Г         ?3

+^02 '(" + ” +

+—) = 0;

Y-m-Y К

7          11

Л-^+Л-^-Ло—^-Ц=0;

• 2    m-Ym-Y

‘2 L         -102 v

2 Y-m-Y         Y-m-Y

+(/2-^ReW=0;

ч^-^'М.

Все уравнения, полученные по МУП и МКТ для двух вариантов схем замещения П-образной и Т-образной, решаются методом минимизации среднеквадратичной погрешности в пакете MathCad и определяется суммарная проводимость рассматриваемого участка сети.

Результаты расчёта показали, что погрешности определения параметров изоляции для отдельных участков сети на порядок больше погрешности определения суммарной проводимости изоляции. Результаты расчета, погрешности определения суммарной проводимости изоляции приведены в табл. 1, из которых следует, что оптимальным является выбор П-образной схемы замещения линии с отпайкой.

Таблица 1

Схема замещения	Метод расчёта	Gs max, %	Gs min, %	Bs max, %	Bs min, %
п	мкг	33,293	-47,492	49,587	-45,116
	МУП	33,293	-47,492	49,587	-45,116
т	мкг	26,499	-57,333	64,817	-40,433
	МУП	27,563	-48,991	75,001	-35,631

На втором этапе анализируются результаты расчетов для случая ухудшения изоляции в фазе А на первом (головном) участке сети, при этом в фазах В и С считаем изоляцию не поврежденной. Расчет цифровой модели линии с отпайкой, имеющей П-образную схему замещения, выполним для нескольких вариантов ухудшения изоляции в фазе А:

DL/=JS6+2ReQS6);

2Ш=^=+5Ке(КЛ);

• 3 ) Ly=JS₆ + 10Re(b);

4)&/=^+50Ке(Г,₆), где Хд] - проводимость изоляции в фазе А на первом участке; К,6 - суммарная проводимость изоляции в фазе В

Х^Хы+Хы+Хьз, здесь Хы - проводимость первого участка, Уы - проводимость второго участка, Ун - проводимость отпаечной линии.

Расчеты цифровой модели выполняются по аналогии с работой [1] для выбранных вариантов ухудшения изоляции. В результате этих вычислений определяются комплексы всех необходимых напряжений и токов. Данные цифровой модели используются при моделировании измерений напряжений и токов для определения параметров изоляции по МУП и МКТ. Найденные параметры изоляции сопоставляем с параметрами изоляции, заданными в цифровой модели. Расчеты по МУП и МКТ дали практически одинаковый результат. Результаты исследования погрешности определения суммарной проводимости изоляции на цифровой модели по МУП, рассчитанные с коэффициентом ^=0,001, приведены в табл. 2.

Таблица 2

Варианты ухудшения изоляции в фазе А	Gs max %	Gs min %	Bs max ' %	Bs min %
1)	13,267	-4,581	48,586	-13,339
2)	10,586	6,512	100,195	29,127
3)	7,341	4,893	197,114	113,548
4)	-15,543	-19,972	1218,074	1089,381

Коэффициент распределения проводимости т, заданный первоначально для всех трех фаз без повреждения, в случае ухудшения изоляции не соответствует распределению проводимости по участкам сети. Поэтому величина погрешности результатов расчета суммарной проводимости изоляции даже при измерении с коэффициентом точности К_р =0,000 получилась отличная от нуля (данные для одного из вариантов ухудшения изоляции приведены в табл. 3).

Таблица 3

Вариант ухудшения изоляции	Gs шах, %	Gs min, %	Bs max, %	Bs mm, %
1)	6,129	6,129	16,363	16,363

Данный метод позволяет зафиксировать факт ухудшения состояния изоляции и определить погрешность результатов расчета суммарной проводимости.