Анализ методов расчета параметров и обоснование математической модели разрушения коры при групповой окорке древесины

Теоретические основы процессов очистки древесины от коры и используемые при этом различные окорочные устройства подробно описаны в работах [1], [11], [12], [13] и др.

Согласно результатам исследований [15], в процессе барабанной окорки в пределах пространства обработки можно выделить 5 зон. Наибольший интерес с позиций механики взаимодействия бревен в окорочном барабане представляет четвертая зона – зона обрушения, где бревна соударяются друг с другом, и пятая – зона удара, в которой бревна ударяются о стенку барабана или о размещенные на его внутренней поверхности рабочие органы.

Интенсивность и качество окорки, а также потери древесины зависят от необходимого и достаточного числа ударов ( N ) определенной силы ( Р ), которые испытывает бревно определенного диаметра ( d ) и длины ( l ) за период времени ( t ) нахождения в барабане, диаметр и длина которого составляют соответственно D и L .

Величины N и Р , в свою очередь, зависят от физико-механических, структурных и прочностных свойств сырья, их состояния (влажности W и температуры T ), а также от размеров емкости барабана, степени его загрузки и угловой скорости вращения ω , определяющих в совокупности скорость ( v ) соударения бревен как между собой, так и с конструктивными элементами барабана. При сухой окорке возникающие ударные нагрузки и силы трения при взаимодействии бревен являются недостаточными для качественной окорки сырья. Необходимо использование специальных коронадрезающих ножей на внутренней поверхности барабана [7].

Стохастическая модель процесса соударений бревен в барабане предложена в работе [1], где качество окорки связано со временем обработки бревен. На основе биномиального распределения числа ударов, приходящихся на элементарную площадку Δ s за период времени t , получено соотношение для определения математического ожидания ( М ) качества окорки:

M = 100

N - 1

¹ - exp -X t ) £

( X t ) z !

где λ – интенсивность ударов или их среднее количество, получаемое одним участком Δ s в единицу времени. Величина N – основополагающий параметр соотношения (1) – зависит от силы удара Р и характеристик коры.

Исходя из теоретических положений данной модели в работе [2] справедливо отмечается, что параметры N и λ не в полной мере отражают такой сложный процесс, как групповая окорка, и недостаточно учитывают закономерности ударных процессов в окорочном барабане в летние и зимние сезоны. В этой связи предложена математическая модель послойного перемешивания древесного сырья в окорочном барабане при положительных и отрицательных температурах [2]. При этом влажность сырья, его физико-механические и прочностные свойства учитываются не дифференцированно, а интегрально путем введения специальных параметров. Так, полученные в ходе выполненных исследований соотношения для определения скоростей движения коры и древесины содержат безразмерный параметр θ, названный в [2] степенью сопротивления элемента коры удару и равный произведению циклической частоты колебаний на период продолжительности удара. Число ударов N принимается равным отношению ударного импульса I , Н • с, необходимого для появления пятна окорки площадью As, к величине ударного импульса 1о, Н • с, возникающего при единичном ударе бревна в процессе его обрушения во вращающемся барабане.

Величину I определяют с учетом характерных размеров бревна и барабана, а также угла наклона а поверхности обрушения. Величина I в конечном счете устанавливается экспериментально в процессе непосредственного нанесения акцентированных ударов по бревну с помощью специально созданных опытных установок. Суммированные значения £ I и ^A s являются интегральными характеристиками необходимых силовых затрат для достижения поставленных технологических и качественных целей окорки в течение ее полного периода времени Т о . Суммарное количество ударов N ^ , которым подвергается вся совокупность элементарных участков A s , определяется геометрическими параметрами бревна и барабана и может быть оценено с помощью соотношения:

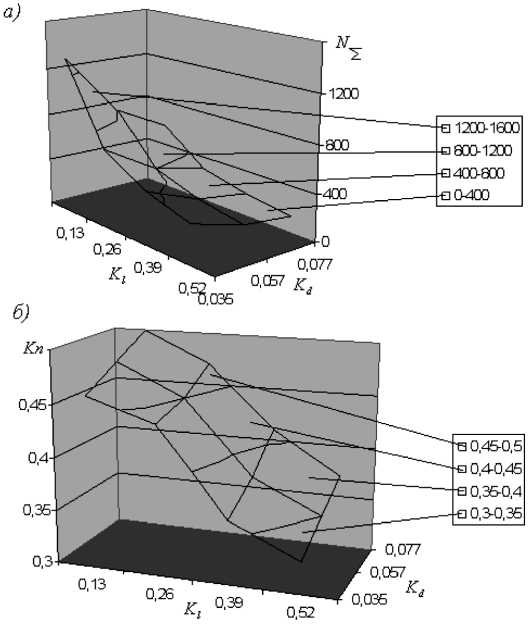
Рис. 1. Графики двумерных функций: а) N _Е = f ( K_d , K i ); б) Kn = f _; ( K d , K )

N

arccos 1 -

K d ²

V

2(1 — K d )²

K 7

где коэффициенты K d и K l представляют собой соответственно отношения диаметров dID и длин lIL . На рис. 1а представлен график зависимости величины N ^ от коэффициента K d в диапазоне его изменения 0,035-0,077 и коэффициента K_l в диапазоне его изменения 0,13-0,52. Как следует из рис. 1а, в процессе окорки материалов реализуются существенно различные условия по фактору числа ударов N ^ , причем при уменьшении размеров бревен число ударов стремительно возрастает.

Объем коры ^V_k в барабане зависит от объема V₆ барабана, коэффициента его заполнения к з , доли коры к_к в общей фитомассе ствола и, особо подчеркнем, коэффициента Kn полнодревеснос-ти укладки бревен в барабане, представленного на рис. 1б, который также зависит от безразмерных коэффициентов K_d и K_l .

Резюмируя результаты исследования [2], необходимо отметить, что оно расширяет диапазон использования стохастической модели [1], однако за рамками теоретического рассмотрения оказался сам процесс соударения бревен как между собой, так и с конструктивными элементами барабана.

Величину импульса I и процесс образования пятна окорки целесообразно оценить с позиций механики контактного разрушения такой сложной среды, как кора и древесина лесоматериалов.

Указанный подход нашел некоторое отражение в работе [10], в которой на базе уравнений движения конечно-элементной модели изучены закономерности изменения сил контактного взаимодействия бревен при их соударении в барабане. Авторы [3] справедливо отмечают, что для определения таких сил необходимы данные о жесткости бревен, которые устанавливаются экспериментальным путем. При этом бревна, взаимодействующие с поверхностью барабана, испытывают значительные по величине нагрузки за счет более высокой жесткости корпуса барабана. В свою очередь, само бревно испытывает неравнозначные по поверхностному распределению силы соударений, и в его торцевых частях наблюдается процесс так называемого размочаливания.

Основной научный результат [4] — прогноз объема бревен, при обработке которых сила соударений может оказаться недостаточной для качественной окорки древесины. Однако и в этом случае рассмотренный процесс взаимодействия бревен не отражает особенности контактного разрушения различных участков массива коры и древесины как сложных структур, обладающих набором характерных физико-механических и прочностных свойств, влажностью и температурой.

Указанные параметры, как свидетельствуют результаты исследований [5], [14], применительно к механической окорке с использованием как тупых короснимателей, так и фрез оказывают существенное влияние на все протекающие про-

цессы отделения коры от древесины. На основании результатов выполненного анализа сформулируем основные положения для обоснования математической модели разрушения коры при групповой окорке лесоматериалов.

Бревно как совокупность цилиндров с диаметром и высотой d представим как совокупность равновеликих по объему шаров с диаметром D_ш = ³ 1,5 d . Количество шаров, приходящихся на одно бревно, равно целой части плюс единица отношения объема бревна V_бр к объему шара V_ш . Два крайних шара назовем торцевыми, остальные – внутренними. Все шары бревна принимаются как мягкие по отношению к жесткой поверхности барабана. Выделим основные схемы взаимодействия мягких шаров с поверхностью барабана, которую, в свою очередь, будем рассматривать как жесткий шар D_ж с бесконечно большим диаметром D_ж = ∞: схема I: « D_ш – D_ш » – взаимодействие двух мягких шаров; схема II: « D_ш – D_ж » – взаимодействие мягкого и жесткого шаров; схема III « D_ш – D_жи » – взаимодействие мягкого шара с жестким, на поверхности которого закреплен нож (твердый индентор).

Представленные схемы будем рассматривать в рамках постановки квазистатических задач ударного взаимодействия двух сферических контактирующих тел [8]. Для обоснования математической модели и оценки ее адекватности на примере сравнения с опытными данными [2] остановимся на схеме II.

При воздействии ударной нагрузки силой Р основными геометрическими параметрами пятна контакта (его глубины и радиуса) являются величины контактного сближения h и радиуса контактной площадки a. Эти параметры функционально связаны между собой, однако ударные процессы в механике контактного разрушения [6], [8] рассчитываются именно через величину сближения h ; с точки зрения качества окорки нас интересует очистка древесины на полную глубину коры. Поэтому в качестве основной геометрической характеристики контакта примем параметр h .

Будем считать [8], что по мере формирования пятна окорки контактная сила F растет и определяется в виде:

F = kh 2 , (3)

где коэффициент пропорциональности k зависит от упругопластических характеристик мягкого шара (модуля Юнга Е и коэффициента Пуассона μ) и его диаметра Dш:

4 E D ш / 2

3(1 - A ²) ^.

k =

Дифференциальное уравнение движения среды на границе контакта при развитии пятна окорки вглубь массива коры имеет вид:

dh dT

2    4 kh ^5/2

v-- т

где v – скорость движения бревна массой m в момент удара.

Наибольшее значение h = hо достигается в момент времени, когда скорость сближения — = 0, dT откуда величина максимального контактного сближения от единичного удара равна:

2/5

h о =

mv ² 4 k

Общая продолжительность удара τ = τ_о при этом составит:

2   1/5

I I

T 0 = 3,2 l — I .                (7)

I vk )

Интегрирование дифференциального уравнения (5) с учетом (6) при начальных условиях: в момент τ = 0 сближение h = 0 позволяет получить функцию изменения во времени контактного сближения h = h ( τ ):

i i ■ Г vnT )z h = hn sinl---------I,(8)

0 (2,94ho J которую будем рассматривать на участке возрастания h от 0 до hо.

Радиус контактной площадки а зависит от h и описывается соотношением:

a = k (1 - a ²) V h .               (9)

E

Силу удара Р вычислим следующим образом: вначале из закона сохранения энергии определяем величину v = (2 gH )^0,5, где H – высота обрушения бревен (максимальное значение H = D – d ), затем из закона сохранения импульсов движения – силу Р = mv / τ_о , причем τ_о определяется из (7).

Расчеты с помощью соотношений (3)–(9) производились таким образом, чтобы в максимальной степени учесть опытные данные [2], в частности, применительно к условиям обработки летних бревен сосны влажностью W = 40–60 %, диаметром d = 0,12 м, длиной l = 2 м в окорочном барабане диаметром D = 2,2 м и длиной L = 4,3 м. При таком диаметре бревна толщина коры сосны hк принята равной 0,02 м. Физикомеханические свойства коры сосны принимались по данным [5] с учетом влияния влажности W на изменение плотности коры ρк. Так, для сухой коры при W = 10 % величина ρк = 370 кг/м3, при W = 40–60 % плотность возрастает до ρк= 687 кг/м3. Тогда масса бревна m достигает 15,55 кг. Расчеты показывают, что в момент удара скорость соударения v = 6,39 м/с, а продолжительность удара τо = 9,62 мс. Контактная сила Р достигла величины 10,32 кН и обеспечила достижение максимальной глубины контактного сближения hо = 0,021 м, превышающей толщину коры hк, то есть в этом случае выполняется условие hо ≥ hк.

На рис. 2 представлены зависимости изменения во времени h ( τ ) и а ( τ ). Как видим, контактное сближение в направлении z отстает от развития контактной площадки в радиальном направлении r , и если возникающие в массиве коры в процессе ударного взаимодействия сдвиговые нагрузки q_s достаточны для ее разрушения, то можно считать, что отделение данного участка на максимальную глубину h_о будет иметь место. Учитывая, что h ≤ a при любом τ , размеры разрушаемых площадок будем оценивать через величину h (оценка снизу).

	a, (cm)
				"^2

О           0,1          0,2          0,3          0,4          0,5 Т, мс

Рис. 2. Изменение во времени удара величин контактного сближения и радиуса контактной площадки: 1 – h ( τ ); 2 – а ( τ )

Величину среднего вертикального давления q_z при ударном взаимодействии шаров определим через параметры h и D_ш [8]:

P пhDш "

qz

Величину радиального (горизонтального) давления с достаточной степенью точности оп ределим через механизм бокового распора [9]:

V qr =--— qz,              (ii)

1 -V

после чего величину давления сдвига q_s на элемент коры определим как приведенное давление:

q s = V q_z + q r • (12)

На рис. 3 представлена зависимость изменения во времени q_s ( τ ); расчеты произведены при значениях μ = 0,25 и Е = 33,29 МПа, установленных через корреляционные связи этих параметров с заданными физико-механическими характеристиками различных сплошных сред, включая лесоматериалы [5], [9].

Сравнивая полученные значения q_s с величиной предела прочности немерзлой коры сосны на скалывание σ_ск = 0,33 МПа [13], можно сделать вывод о том, что с начального момента времени удара вплоть до достижения максимального сближения выполняется условие:

qs ≥ σск, (13) то есть участок размером Δs = πho2 = 1385 × × 10-6 м2 будет полностью окорен на полную глу- бину сближения ho. Величина ударного импульса при этом составила Iу = 99,34 Н ∙ с.

^5, M	Па
			y = c	,360x^'37
			R2	= 0,976
	0	1         0,2        0		3        0	4        0,	5      T, MC

Рис. 3. Изменение во времени удара величины приведенного давления в массиве коры летней сосны

Уместно отметить, что для мерзлых бревен сосны величина σ_ск ≥ 1,1 МПа [13] и возрастает до 1,8 МПа с понижением температуры Т до 20 ^оС. Это означает, что в таких условиях установленные значения q_s недостаточны для реализации механизма сдвига в пределах элементарной площадки и не обеспечивают надлежащую окорку данного участка. В этом случае необходимо либо увеличивать силовое воздействие, включая использование ножей, либо улучшать состояние бревен – обрабатывать их паром или водой с целью снижения величины σ_ск до необходимого уровня. В обоих случаях это требует дополнительных затрат, а при использовании ножей обусловливает рост потерь древесины. Влияние температуры на силы сцепления коры и процессы ее разрушения подробно рассмотрены в работе [5], а особенности контактного разрушения при статическом внедрении индентора – в [14].

Возвращаясь к анализу условий обработки бревен летней сосны при выполнении условия (13), скажем, что для окорки элементарного участка достаточно одного удара о жесткую поверхность барабана, то есть интегральные характеристики ∑ I_у и ∑Δ s совпадают с полученными одинарными ^у значениями I_у и Δ s .

Общий объем коры в оубрабатываемых бревнах для данных условий расчета ∑Vк = 0,059 м3 при следующих значениях технологических коэффициентов: kз = 0,5, kк = 0,15, Kn = 0,36. Максимально возможный объем разрушенной коры в пределах зоны контакта в результате единичного удара Vк = πhk3 = 127 ∙ 10-6 м3, то есть минимально необходимое число ударов по всем элементарным участкам бревен N∑ = 465, что удовлетворительно согласуется с данными рис. 1а при значении коэффициентов Kd = 0,055 и Kl = 0,47. Сравним полученные результаты с опытными данными [2], которые показывают, что для окорки аналогичных бревен также достаточно одного удара по элементарному участку коры при величине ударного импульса Iу = 106 Н ∙ с с образованием пятна окорки площу а- дью Δs = 1486 ∙ 10-6 м2. Как видим, теоретические расчеты согласуются с опытными данными: относительная погрешность δ при оценке импульса составляет 6,7 %, при оценке размеров пятна δ = 7,3 %.

Выполним аналогичный расчет для условий окорки летних бревен осины с плотностью коры ρ_к = 758 кг/м³ при W = 40–60 % и толщине h_к = 0,05 м. Упругопластические характеристики: μ = 0,25, Е = 146,83 МПа. Масса бревна m = 17,15 кг, время удара τ_о = 5,52 мс при максимальной силе Р = 19,82 кН и ударном импульсе I_у = 109,5 Н ∙ с.

Расчет показал, что максимальное контактное сближение h_o = 0,0112 м, а величина q_s достигла 1,26 МПа и превысила во всем диапазоне своего изменения значение прочностной характеристики немерзлой коры осины: σ_ск = 0,79 МПа. Для мерзлой коры осины уже при Т ≤ -10 ^оС величина σ_ск ≥ 1,6 МПа.

Таким образом, для летних условий обработки бревна осины разрушение в пределах элементарной площадки Δ s = 456 ∙ 10^-6 м² на глубину h_o , как и при окорке сосны, произойдет. Вместе с тем за один удар очистка массива коры осуществится только на глубину h_o = 1,12 см, и для окорки бревна на полную глубину h_к = 5 см потребуется не менее N = 5 ударов. На данном этапе обоснования математической модели не будем учитывать механизмы уплотнения коры в процессе циклического ударного взаимовоздейс-твия с жесткой поверхностью барабана (индентора), то есть принимаем, что на каждом новом цикле процесс удара воспроизводится в полном объеме. Тогда имеем: ∑ I = NI = 548 Н ∙ с и ∑Δ s = N Δ s = 2284 10^-6 м². ^{у у}

Сравним полученные результаты с опытными данными [2] при окорке бревен осины в аналогичных условиях, где установлены следующие показатели разрушения коры: N = 7, ∑ I = 630 Н ∙ с ( δ = 14,96 %) и ∑Δ s = 2350 ∙ 10^-6 м² ( δ = ^у 2,89 %).

Сравнение погрешности расчетов при окорке кряжей сосны и осины показывает, что при механическом воспроизводстве ударных процессов наблюдаются более высокие расхождения теоретических данных с опытными. Однако результаты расчетов следует признать удовлетворительными. Дальнейший учет в математической модели особенностей разрушения коры при циклических нагрузках, включая ее уплотнение и как следствие – изменение упругопластических и прочностных свойств, приведет к росту необходимого числа ударов N и повышению точности оценок.

Подводя итог и анализируя результаты математического моделирования процессов контактного ударного взаимодействия мягкого шара (элемента бревна) с жестким шаром (поверхностью барабана), можно сделать вывод об адекватности принятых методических положений реальным условиям реализации процессов разрушения элементарного участка коры при групповой окорке древесины. Разработанная модель позволяет более детально рассмотреть предложенные схемы ударного взаимодействия I–III для разнообразных технологических условий групповой окорки лесоматериалов.

Материалы статьи получены при выполнении НИР, в рамках ФЦП «Научные и научнопедагогические кадры инновационной России», в рамках мероприятия 1.3.1. Контракт П 1209.