Анализ методов расчета тоннельной обделки

Существующие в настоящее время методы расчета тоннельной обдели можно разделить на три большие группы:

• 1.    Методы расчета на заданные нагрузки, основанные на положениях строительной механики.

• 2.    Методы расчета, учитывающие совместное деформирование обделки и окружающего породного массива, основанные на положениях теории упругости и механики сплошных и дискретных сред.

• 3.    Приближенные численные методы расчёта, основанные на применении метода конечных элементов, реже метода граничных элементов.

В методах расчета первой группы нагрузка на крепь рассматривается как внешняя сила, величина которой не зависит от деформационно-силовой характеристики крепи. На начальном этапе развития методов, обделка рассматривалась как отдельная конструкция, загруженная внешней нагрузкой по аналогии с расчетом несущих конструкций наземных частей зданий и сооружений. Рассчитывалась только сводчатая часть обделки, которая рассматривалась как пологий свод с абсолютно жесткими пятами.

В дальнейшем обделка стала рассматриваться как стержневая система в упругой среде. В основу решения положено допущение о линейной зависимости между напряжениями и деформациями грунта (гипотеза Винклера). Первые работы, основанные на рассмотрении упругого взаимодействия стен тоннельной обделки и подземной выработки, принадлежат проф. С.С. Давыдову, опубликовавшему в 1934-1935 гг. методику расчета обделки с массивными вертикальными стенами.

Рассмотрим основные предпосылки данной методики. Тоннельные обделки, сооружаемые горным или щитовым способом, являются конструкциями распорного типа, работающими в упругой среде грунта. Зазор между обделкой и стенами выработки, образующийся в процессе производства работ, плотно заполняется цементным раствором, нагнетаемым под значительным давлением. Это обеспечивает совместность деформаций обделки и горных пород и дает возможность рассматривать конструкцию и окружающую среду как единую упругую систему.

Под действием внешних активных нагрузок тоннельная обделка деформируется, изменяя свое положение относительно контура выработки. На той части контура, где перемещения обделки происходят в сторону выработки, обделка деформируется свободно, не взаимодействуя с породой (рис. 1).

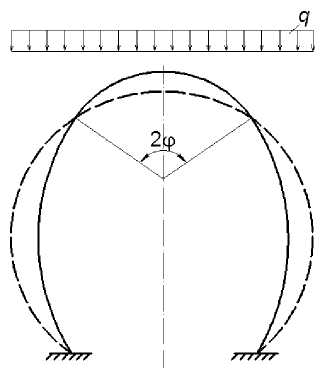
Рис. 1. Общая схема деформирования тоннельной обделки в упругой среде грунта

Эта часть контура носит название безотпорного участка и характеризуется возникновением в обделке значительных изгибающих моментов.

На остальной части контура тоннельная обделка смещается в сторону породы, вызывая с ее стороны сопротивление – упругий отпор, ограничивающий деформации конструкции и возникающие в ней моменты.

В процессе развития методов расчета первой группы на практике получили применение следующие виды расчетных схем для соответствующих типов обделок: пологий свод, опирающийся на породу; пологий свод, опирающийся на вертикальные стены; подъемистый свод, опирающийся на породу; подъемистый свод, опирающийся на обратный свод.

Наибольшее практическое применение в нашей стране получил метод расчета тоннельной обделки Метрогипротранса (Б.П. Бодров, Б.Ф. Маэрти и др.). Первоначально разработана методика расчета для тоннелей круглого сечения, далее она была распространена и на обделки горных тоннелей [1].

С началом широкого внедрения в расчетную практику ЭВМ и появлением специализированных программ методика Метрогипротранса стала постоянно развиваться. Стал возможным отказ от априорного задания активной и реактивной зон обделки благодаря уточнению условий контакта на основе введения в рассмотрение упругих стержней, моделирующих отпорные свойства массива. Уточнены условия контакта обделки с массивом, появи- лась возможность задания начальных усилий в упругих связях, моделирующих отпорные свойства грунтового массива, а также учета сил сцепления между обделкой и грунтом. Исследования по совершенствованию расчетных методов первой группы продолжаются и в настоящее время.

К принципиально иному типу относятся расчетные схемы второй группы, которые развиваются в рамках механики подземных сооружений и основаны на использовании моделей механики сплошных и дискретных сред. Их отличительная особенностью является рассмотрение не только обделки, но и вмещающего выработку грунтового массива (система «крепь – массив»). Расчетная схема обделки представляет собой плоскую схему контактного взаимодействия обделки с деформируемым массивом (рис. 2). Основные виды воздействий, которым повергается система «крепь – массив» являются собственный вес пород, тектоническое поле начальных напряжений, давление подземных вод, сейсмические воздействия и др. При этом характер и величина воздействий на обделку зависят от ее деформационносиловой характеристики, геометрической изменяемости, а также технологии сооружения тоннеля [2].

Обделка может быть представлена монолитной конструкцией, обладающей изгибной жесткостью; сборной конструкцией со связями растяжения в стыках и с шарнирными стыками, набрызгбетонным покрытием, многослойной конструкцией.

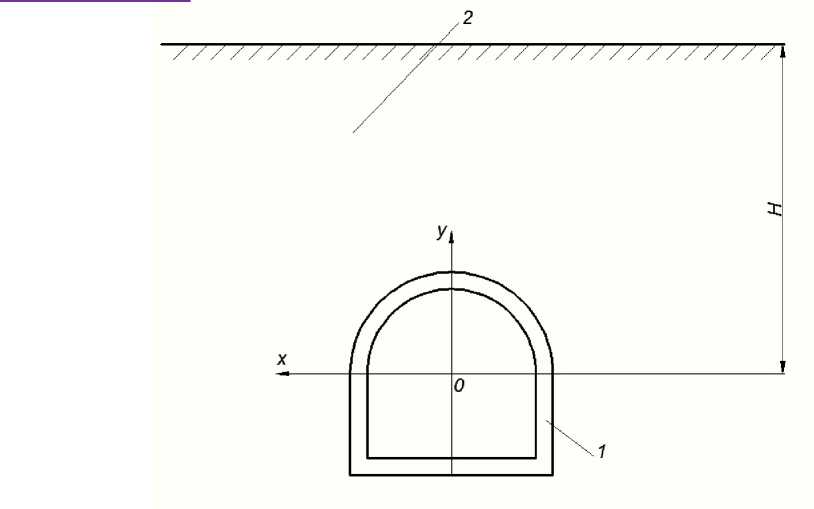
Рис. 2. Расчетная схема обделки в массиве пород:

1 – обделка; 2 – породный массив; H – глубина заложения тоннеля

При ее расчете не определяются неизвестные внутренние усилия в конструкции обделки, как при применении схем первой группы, а осуществляется анализ напряженно-деформированного состояния системы «крепь – массив». В большинстве случаев рассматривается плоская задача в рамках линейно деформируемой модели массива пород.

Разработка схем второй группы началась с простейших осесимметричных задач. А.Н. Динником впервые рассмотрено решение задачи по определению напряжений в упругой среде, ослабленной незакрепленной круглой выработкой в плоской постановке. Г.П. Савиным получено решение задачи определения напряженно-деформированного состояния закрепленной выработки с помощью решения Ламе для толстостенной трубы.

Большой вклад в развитие механики подземных сооружений и методы расчета обделок тоннелей внесли Н.С. Булычев и Н.Н. Фотиева. В их трудах рассмотрены методы расчета обделок произвольного поперечного сечения, в том числе многослойных с использованием теории функций комплексного переменного, развитой в работах Н.П. Мусхелишвили [2]. Основные положения расчета обделки круглого сечения представлены в п. 3.4.

В настоящее время методы расчета обделок 2 группы продолжают совершенствоваться. В частности, получено решение для оценки напряженное состояние обделок параллельных подземных сооружений произвольного поперечного сечения (П.В. Деев), расчета тоннелей, закрепленных анкерной крепью (Р.Ю. Завьялов), сооружаемых в сейсмических районах (А.С. Сам-маль), взаимодействующих с породами в состоянии запредельного деформирования и разрушения (И.В. Баклашев) и др.

Несмотря на достигнутые успехи, область применения методов расчета второй группы весьма ограничена, особенно в случае сложной пространственной геометрии исследуемых объектов.

На помощь здесь приходят приближенные численные методы расчёта тоннельной обделки третьей группы. Они основываются на использовании метода конечных элементов, а также в более редких случаях метода граничных элементов.

Сущность метода конечных элементов (МКЭ) заключается в том, что область, занимаемая телом, разбивается на конечное количество подобластей, например, треугольников для плоской модели или тетраэдров для пространственной (рис. 3). Последние носят название конечных элементов (КЭ), а сам процесс разбивки – дискретизацией.

Затем внутри каждого элемента разбиения задается приближенная функция в максимально простой форме – обычно это полином, как правило, третьей или четвертой степени. Точность приближения повышается за счет более мелкого разбиения области. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов и ограничивается только возможностями компьютерной техники.

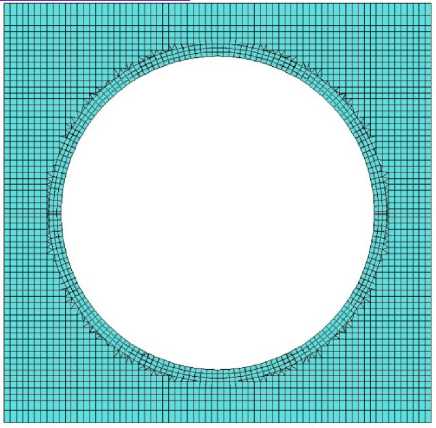
а)

Рис. 3. Примеры конечно-элементных моделей:

б)

• а) плоская; б) объемная

Широкому распространению МКЭ для решения геомеханических задач способствовали труды Б.З. Амусина и Д.К. Фадеева. Сегодня МКЭ применяется для решения самого широкого класса задач при проектировании новых и анализе напряженно-деформированного состояния существующих транспортных тоннелей с помощью современных программных пакетов ANSYS, COSMOS/M, Лира-Windows, SCAD GROUP, STAAD Pro, FEM models, PLAXIS, Robot Millennium, FLAC (Itasca Company), ABAQUS, ADAPT, CRISP, SOFiSTiK, CivilFEM, LS-DYNA, Z_SOIL и др.