АНАЛИЗ МНОГОМЕРНЫХ ДАННЫХ ПО СОСТАВУ ГАЗОВ, ВЫДЕЛЯЕМЫХ ИЗ РАЗЛОМОВ ЗЕМНОЙ ПОВЕРХНОСТИ

Газовые смеси, выделяемые из разломов земной коры, как правило, содержат несколько компонентов. Чаще всего встречаются: СО 2 , СН 4 , Не, Н 2 S, Н 2 , N 2 , O 2 и другие в зависимости от места расположения разлома [1]. В многомерном пространстве данных, например, семь компонентов представлены в виде точки в семимерном пространстве. Множество замеров, выполняемых в течение некоторого промежутка времени, образует "облако", которое может состоять из нескольких тысяч точек данных. При этом концентрация каждого компонента в "облаке" и в целом спектр зависят от внутренних процессов, происходящих в земной коре, т.е. содержат информацию о разломе как геологическом объекте. Если эти процессы близки и повторяются, также близки интенсивности выделяемых газов, и в многомерном пространстве каждый из таких процессов образует группу (кластер) близко расположенных точек. В результате длительного наблюдения с использованием различных приборов может быть установлена статистическая связь между спектральным составом газов и внутренними физико-химическими процессами в земной коре. В дальнейшем, используя полученные результаты, по единичным замерам состава газов можно с некоторой вероятностью предсказать характер происходящих в земной коре процессов.

Этот подход может быть положен в основу метода экспресс-прогноза текущего состояния зем- ной коры на основе масс-спектрометрического мониторинга состава газов. Процедура прогнозирования производится в три этапа.

Первый этап:

– наблюдение в течение продолжительного времени с регистрацией спектров газов — формирование обучающей выборки;

– формирование кластеров спектров и установление их связи с физико-химическими процессами в земной коре.

Второй этап:

текущее измерение спектра газов и определение его принадлежности тому или иному кластеру по минимуму расстояния между его центром (цен-троидой) и точкой спектра в многомерном пространстве.

Третий этап:

выводы о вероятности процессов, происходящих в земной коре.

ОБРАБОТКА ДАННЫХ

Теория

Для накопления данных о составе и интенсивности газов, выделяемых в разломах земной поверхности, целесообразно проводить параллельные замеры в нескольких разломах в одном геологическом районе в течение длительного промежутка времени с одновременной регистрацией процессов, происходящих в земной коре, с помощью других приборов. Эти данные назовем обучающей группой, т.к. в дальнейшем они необходимы для сопоставления с текущими замерами и принятия решения о возможных последствиях.

В результате одного замера регистрируется несколько компонентов газа, образуя вектор-строку [ x_{i ,1}, x_{i ,2}, ..., x_{i , j} ], где x _i,j — интенсивность j- го компонента i- го замера обучающей группы, причем i = 1,2,..., I . Набор из I замеров J регистрируемых компонент газа образует ( I , J ) обучающую матрицу X , столбцы которой обозначим как X _j : X = [ X 1 ,..., X _p..„ X J ] [2].

После достаточно длительного наблюдения c выполнением одного-двух замеров в сутки обучающая матрица X содержит ряд групп (кластеров), близких по времени измерений. Кластеры отличаются интенсивностью, а иногда и составом газов в зависимости от характера процессов, происходящих в земной коре в момент измерений.

Обозначим через Xk k -й кластер, k = (1, 2, 3, …, K), где K — число кластеров. Кластер представляет собой матрицу из Ik строк (Ik << I ) и J столбцов. Каждая строка матрицы образует в J-мерном пространстве точку, а все строки — "облако" из Ik точек. Центр этого "облака", центроида кластера, имеет координаты в виде средних г                      г               г                            г значений по столбцам: X = [X1 , X2,...., Xj] и дисперсий °k = Н, а2,..., CTJk].

Идентификация новых замеров

Разбиение обучающих замеров на кластеры и их идентификация с определенным процессом в коре завершает обучение системы обработки данных. Для надежной идентификации новых замеров по обучающим данным число элементов в кластере должно быть как минимум больше трех.

Пусть очередной замер воздуха в разломе — X d = [ x d ,1 , x d ,2 ,..., x d , J ] , где x dj — текущая ^интенсивность компонента газовой смеси в разломе. Задача состоит в том, чтобы по этому замеру с некоторой вероятностью можно было судить о физико-химических процессах в недрах Земли, для чего оценим расстояние в многомерном пространстве между точкой X _d и центроидой k -го кластера X ^k . Это расстояние в евклидовой метрике определяется как

-.           -,X

P k = ( X d - X ^k )( X d - X ^k ) ,           (1)

‘

— символ транспонирования матрицы.

Принадлежность замера X _d тому или иному кластеру k ₀ определяется по минимуму расстояния ρ _k :

P k 0 = "'ⁿⁱ P k ).

Очевидно, что величина ρ _k определяет также вероятность определенного процесса, происходящего в момент замера: при p_k ^ 0 эта вероятность должна быть равна единице, а при удалении точки X _d от центроиды — уменьшаться до нуля. Этим свойством обладает функция плотности вероятности P ( X _d ) случайной величины X _d со средним значением X ^k и дисперсией данных, входящих в этот кластер, σ _k ² :

P (X d ) =

_               _/

= W • exp {- 2 ( X d - X ^k ) K ^{- 1} ( X d - X ^k )

где K — ковариационная матрица: K =

'!

=^E ( X - X ) • ( X - X ) ,

E — символ математиче-

ского ожидания, W — нормирующий множитель. Из условия равенства вероятности P ( X _d ) единице при p ^ 0, должно быть W = 1 . Условие принадлежности замера X _d кластеру X ^k имеет вид: P ( X _d ) <  а , где величина а выбирается методом экспертной оценки.

Метод главных компонент

Однако непосредственное использование приведенных формул для разделения данных на кластеры и расчета величины P сопряжено с ошибками, вызванными наличием большого числа параметров J и корреляционных связей между столбцами матрицы X . Для сжатия данных, сокращения размерности пространства измерений используют ортогональное преобразование данных в пространство главных компонент — метод главных компонент (МГК) [3].

Для перехода в пространство ГК формируется новая матрица, состоящая из всех строк матрицы X и строки X _d . Обозначим эту матрицу как X 1 . Тогда в новой системе координат:

A

X 1 = T • P ' + e = ^ t _v p ' + e ,             (4)

j = 1

где p j — собственные функции ковариационной матрицы K. Матрицу T называют матрицей счетов T = [T1, T2,..., TA ], ее размерность — (Ix A); матрицу P называют матрицей нагрузок, ее размерность — (I × A); e — это матрица остатков (шумов) размерности (I x J); векторы-столбцы Tj (j =(1, 2,..., A)) называют главными компонентами (ГК), A — число главных компонент. Величина A значительно меньше числа переменных J. Это означает, что основная информация сосредоточена в нескольких первых ГК. Последняя строка этой матрицы, вектор Td — координаты параметров тестируемого состава воздуха в пространстве ГК: Td = [td,1, td,2, ..., td,a ] .

Из данных в новой системе координат формируются кластеры T ^k — матрицы из I_k строк ( I_k <<  I ) и A столбцов. Центроида кластера имеет координаты в виде средних значений по столбцам        T ^k = ^[ T , T 2 k ,...., T A ^]     и дисперсий

2   22    2

° k = [ ^ 1 k , ^ 1 k , ..., ° Ak ] .

Свойство разложения по ГК таково, что дисперсия быстро уменьшается уже к четвертой ГК, а столбцы матрицы T ^k не коррелированы, т.е.

T ^k (T ^k У = mn

f o

1 a ² k

при n ^ m , при n = m .

Учитывая это обстоятельство, в новой системе координат вероятность принадлежности нового замера кластеру k вычисляется по формуле:

там процессам. Затем, используя подходящий алгоритм кластеризации [4], разбивают накопленные данные на кластеры X ^k , каждый из которых отображает определенный физико-химический процесс в земной коре. Может быть использован другой вариант разбиения накопленных данных на кластеры: сортировка данных по принадлежности к процессу, происходящему в земной коре в момент замера состава выделяемых газов.

На этапе диагностики выполняется следующая последовательность операций:

• 1.    Измеряются состав и концентрация диагностируемого источника газа и формируется вектор– строка X d = { x_d ,1 , x d _2 ,..., ^х , , j } .

• 2.    Отображение данных матрицы X и замера X _d , т.е. матрицы X 1 = [ X ; X _d ] , в пространство ГК (4).

• 3.    Вычисляется расстояние по формуле (6) и определяется ближайший кластер по минимуму расстояния (2).

• 4.    Определяется вероятность P по формуле (5) 5. Анализ результата вычисления вероятности.

ПРОВЕРКА АЛГОРИТМА

Проиллюстрируем изложенную выше теорию на примере реальных 1024 замеров состава газа, выполненных в Ленинградской области.

На рис. 1 показан пример масс-спектра одного из замеров состава газовой смеси: CH 4 , N 2 , O 2 , CO 2 , Ar. Замеры выполнялись ежедневно один

P(Td ) = exp {-2(Td - Tk)' °-2 (Td - Tk )j =

1 ^A

= exp < — 2

P 2 ^

j = i

( t d , j — t ^k ) 2 ' ^ k² j

.

Евклидово расстояние от замера с индексом d до центроиды k -го кластера равно:

ρk

= ( T d - T ^k ) ' ( T d

A

- T ‘ )=U( t d , ,

I j = 1

ОПИСАНИЕ АЛГОРИТМА

Обработка данных состоит из двух этапов: обучение и диагностика .

На этапе обучения формируется обучающая матрица X путем набора данных о составе и концентрации компонентов воздуха в местах выделения газа и привязки этих данных к происходящим

1/2

- ? * П . (6)

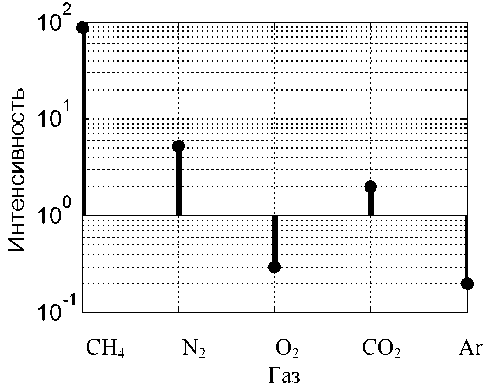
Рис. 1. Спектр одного из замеров состава смеси

I о л н о о

I со

S о

I ф н

I S

Кластер 1

Кластер 3

День замера данных

Рис. 2. Связь кластеров и времени наблюдений

раз в сутки. Данные, накопленные в течение продолжительного времени с использованием иерархического агломеративного алгоритма [4], разделены на кластеры, каждый из которых состоит из более чем десяти замеров близких по интенсивности компонентов газа. На рис. 2 показано расположение трех кластеров на временнóй шкале продолжительностью более 1000 дней наблюдений: каждый кластер связан с определенным временем и, соответственно, процессом, происходящим в земной коре. (На рисунке приведен только метан.)

В табл. 1 (столбец 2) приведено евклидово расстояние одного из замеров до девяти кластеров, вычисленных по формуле (6). Из таблицы следует, что замер принадлежит третьему кластеру с вероятностью 0.33, вычисленной по формуле (5) (столбец 3).

Табл. 2. Характеристики точек-замеров кластера 3

мера из кластера 3	Расстояние от замера до центроиды кластера 3	Вероятность соответствующего геособытия
1	0.3442	0.0982
2	0.4309	0.1366
3	0.3153	0.1456
4	0.484	0.1709
5	0.7648	0.1825
6	1.0106	0.1833
7	0.7499	0.2241
8	0.4035	0.3371
9	0.7676	0.3864
10	0.303	0.428
11	0.143	0.4333
12	0.0725	0.4882
13	0.1344	0.546
14	0.1367	0.5643
15	0.0169	0.7377

Далее выберем пятнадцать замеров, принадлежащих третьему кластеру, но расположенных в разных точках "облака" этого кластера. В табл. 2 во втором столбце приведены расстояния до центроиды кластера, а в третьем столбце — вероятность события в земной коре, вызвавшего соответствующее выделение газов. Видно также, что чем ближе расположен замер к центру кластера, тем больше вероятность события. В приведенном примере замер номер 1 вероятнее всего принадлежит другому кластеру. Тогда по приведенной выше методике находят этот кластер и определяют соответствующую вероятность.

ЗАКЛЮЧЕНИЕ

Табл. 1. Пример расположения замера относительно кластеров

№ кластера	Расстояние от замера до центроиды кластера	Вероятность
1	105.8	0
2	101	0
3	0.4	0.3371
4	136.91	0
5	4.5	0.007
6	664.4	0
7	28	0
8	67.6	0
9	217.4	0

Система диагностики процессов в земной коре, состоящая из прибора для количественного измерения состава воздуха в местах выделения газа и средства обработки данных с возможностью обучения и определения вероятности происходящих в земной коре процессов, обеспечивает экспресс-анализ состояния земной коры. Диагностика с определением вероятности принадлежности состава выделяемого газа одному из обучающих кластеров позволяет составить общую картину вероятных событий в земной коре и при необходимости принять соответствующие решения относительно вероятности определенных геологических процессов в данном регионе.

Работа выполнена в ИАП РАН в рамках государственного задания № 122040600002-3.