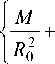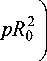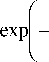Анализ многомодовых волоконных световодов с произвольным осесимметричным профилем показателя преломления на основе модифицированного метода приближения Гаусса

В настоящее время многомодовые волоконные световоды находят широкое применение в различных приложения волоконной оптики. В первую очередь это относится к типовым градиентным многомодовым оптическим волокнам, а также многомодовым оптическими волокнами, оптимизированным для работы с лазерными источниками оптического излучения, которые эффективно используются на высокоскоростных локальных сетях передачи данных. Другое направление - это много- и маломодовые волоконные световоды специального назначения, отличающиеся сложным (например, W-образным) профилем показателя преломления. Подобные оптические волокна находят широкое применение в отдельных компонентах высокоскоростных одномодовых волоконно-оптических линий передачи, таких, как, например, компенсаторах хроматической дисперсии на модах высших порядков. Указанные приложения требуют расчета параметров передачи не только основной моды, но и мод высших порядков.

На сегодняшний день известно огромное число методов анализа волоконных световодов. Некоторые из них являются общими подходами в решении задач анализа круглых оптических волноводов, другие были разработаны для частных приложений волоконной оптики. Большинство из указанных методов эффективно применяются для определения параметров передачи основной моды волоконного световода с произвольным профилем показателя преломления, некоторые позволяют рассчитать характеристики высших мод оптических волокон с идеальными профилями. Однако переход к поставленной задаче расчета параметров передачи не только основной моды, но и мод высших порядков многомодовых волоконных световодов с произвольным профилем показателя преломления требует многократного решения систем линейных алгебраических уравнений, что существенно повышает требования к ресурсам вычислительной техники.

В данной работе представлен альтернативный метод анализа многомодовых волоконных световодов с произвольным осесимметричным профилем показателя преломления. Метод является обобщением модифицированного метода приближения Гаусса [1] на указанный случай. В отличие от известных решений на основе приближения Гаусса [1 - 7], многомодовое оптическое волокно с произвольным осесимметричным профилем показателя преломления рассматривается как волоконный световод с многослойным профилем показателя преломления. При этом профиль показателя преломления сердцевины исследуемого волоконного световода представляется в виде конечного числа N оболочек, в пределах которых значение показателя преломления остается постоянным. Это позволяет записать вариационное выражение для параметра моды в сердцевине U и характеристическое уравнение, решением которого является эквивалентный нормированный радиус пятна моды R 0 , в виде конечных вложенных сумм.

В работе представлены результаты оценки погрешности предлагаемого метода. Приведены данные расчета параметров передачи направляемых мод, а также их сравнения точными решениями для ступенчатого и неограниченного параболического профилей показателя преломления.

• 1 . Приложение модифицированного метода приближения Гаусса для анализа многомодовых волоконных световодов

с произвольным осесимметричным профилем показателя преломления

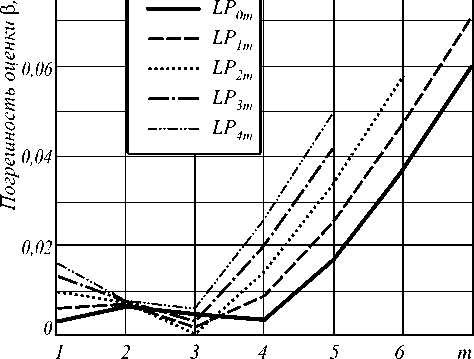
В соответствии с вышесказанным, предлагаемый метод является обобщением модифицированного метода приближения Гаусса на случай расчета параметров передачи направляемых мод произвольного порядка, распространяющихся в сердцевине многомодового оптического волокна с произвольным осесимметричным профилем показателя преломления. В основе приближения Гаусса лежит аппроксимация поля моды Fm(l)(R) волоконного световода с произвольным профилем показателя преломления полем моды слабонаправляющего волоконного световода с некоторым параболическим профилем показателя преломления [1 – 9]:

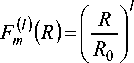
I l ( ¹ )

L m - 1

' R 2 '

. ^R 02 ,

exp

V

R ² 1

2 R 0 ²

1 2 = 2 V ^to f ( R ) F¹ ) ) 2 RdR ,

^R 0 0

соответственно. После преобразований, использующих рекуррентные формулы относительно степени ортогональных многочленов, формулы интегрирования полиномов Лагерра, свойство ортогональности полиномов Лагерра а также формулы умножения и возведения в степень рядов [5-6] интеграл I 1 приводится к выражению вида:

где l – азимутальный порядок моды; m – радиальный порядок моды; R = r / a - нормированный радиус; r

– координата; a – радиус сердцевины волоконного световода; R0 = p 0 / a - нормированный радиус пятна моды; p 0 - радиус пятна моды; Lm-1 - поли- ном Лагерра.

Для определения R0 воспользуемся известным скалярным вариационным выражением для пара- метра моды в сердцевине U круглого слабонаправляющего волоконного световода [1 – 7]:

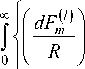
U ²

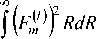
где V = kan ₀ V2 A - нормированная частота (волноводный параметр), определяемая первичными параметрами ОВ; k=2 n / X - волновое число; X - рабочая длина волны; А = ( n 0 - n ²)/ 2 n 0 - параметр высоты профиля показателя преломления; n 0 – значение показателя преломления в центре сердцевины; n 1 – показатель преломления оболочки; f(R) – функция профиля показателя преломления, удовлетворяющая выражению, описывающего профиль показателя преломления ОВ:

n ² ( R ) = n 0 [ 1 - 2 А. f ( R ) ] .                         (3)

После подстановки (1) в (2) и выполнения соответствующих преобразований вариационное выражение для параметра моды в сердцевине примет следующий вид:

2_ ⁽ m - 1 ) ! _2_

U " ( 1 + m - 1 ) ! R 02

M

I ¹ = R 2 , R ₀

где [10 – 11]:

M = (1 + m -1) !(31 + 2 m -1) +

( m - 1 ) !

2 m - 2                     2 m - 2

+ 2 1 ² Z D q ( q + 1 - 1 ) ! - 4 1 Z C q ( q + 1 ) !, q = 0                          q = 0

mi ^{n (} q , ^m - 1 ) z x , x

D q = Z a q ( L m ) - 1 ) a q - p ( L⁽ m ) - 1 ) , p = max ( 0, q - m + 1 )

min ( q , m - 1 )    / x / x

Cq =      Z aq (L(m)-1 )^q-p (L^t!)), p=max(0, q - m+1)

где a_q ( L ^ ^ ) , b_q ( L ^ + 1 ) ) - коэффициенты полиномов Лагерра L ^ ⁾_ ₁ и L ^ ¹ 1 ) , соответственно, определяемые из формулы явного выражения полинома Лагерра [12-13]:

.

В отличие от известных решений на основе приближения Гаусса, волоконный световод с произвольным осесимметричным профилем показателя преломления рассматривается как волоконный световод с многослойным профилем показателя преломления. При этом профиль сердцевины представляется в виде конечного числа N оболочек, в пределах которых значение показателя преломления остается постоянным:

to

xf

' ^d F¹ ) 1 ²

dR

V 2

I12 1 R+

V ² f ( R Ж¹ ) ] 2 RdR .

^{n ( R} ) =

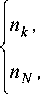
k <  R <  k + 1 , NN

1 <  R < +to

0 < k <

N - 1

N

Выражение (4) перепишем в виде суммы двух интегралов:

U 2 = 11 + 12, где

В этом случае функция произвольного профиля показателя преломления может быть записана в сле-

дующем виде:

^ to

1 1 =■ '

^R 0 0

' dF , ¹ ) 1 ²

dR

V /

+21(f(■

⁺ R 2 \ ^m /

RdR ,

f ( R ) =

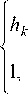
k _n k + 1 — <  R <  , NN

1 <  R < +to

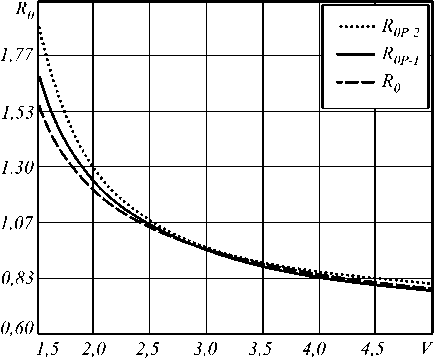
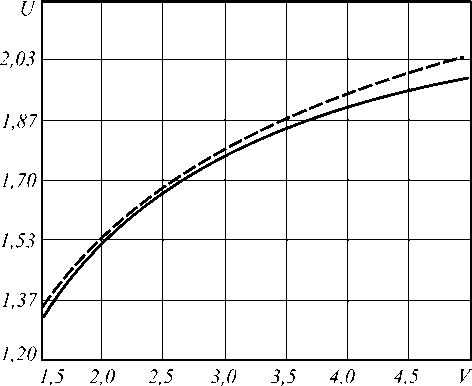
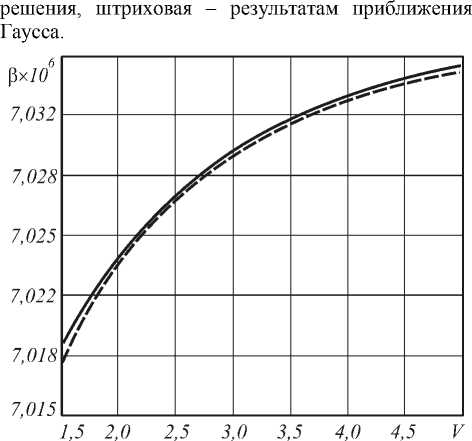
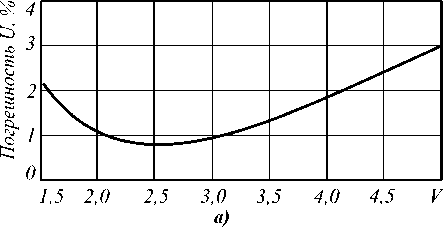
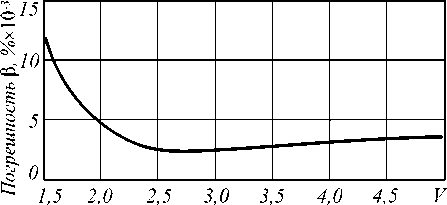
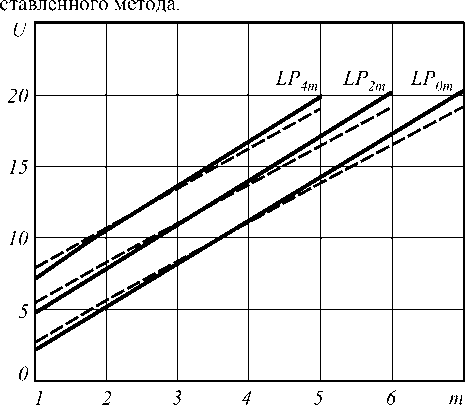
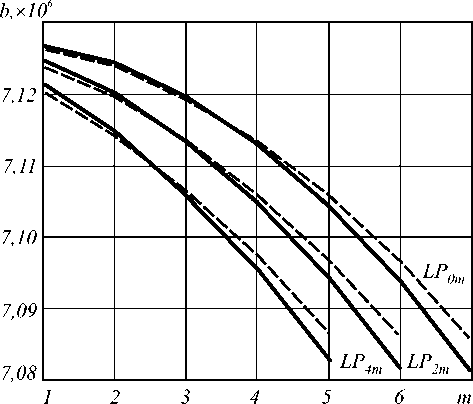
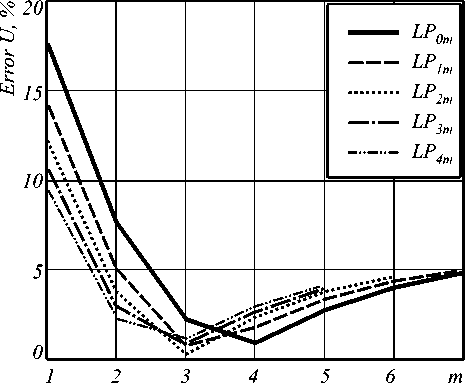
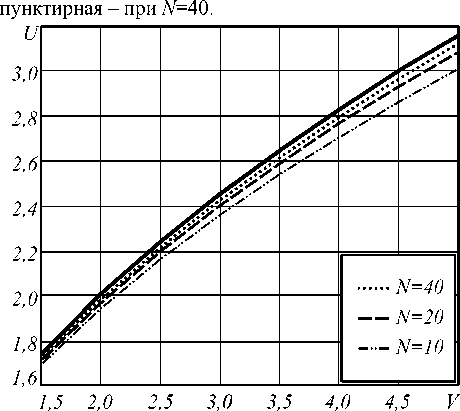
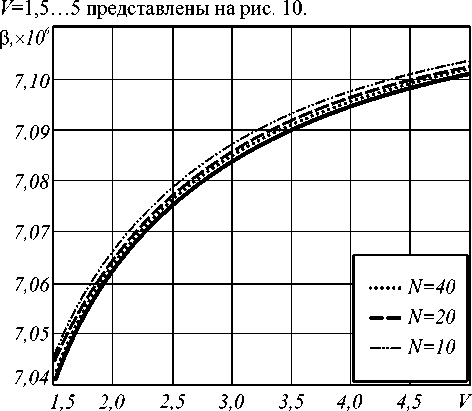
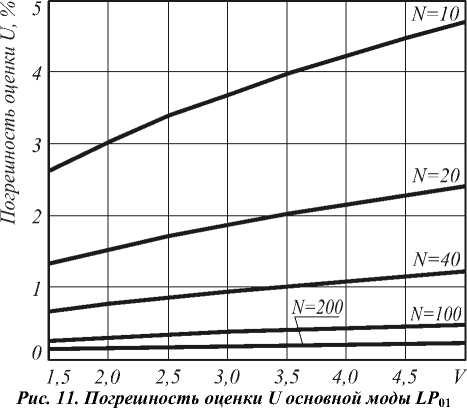
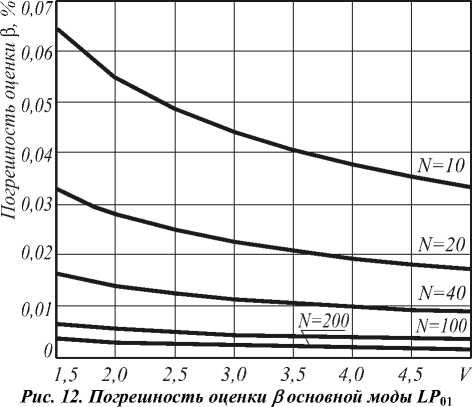
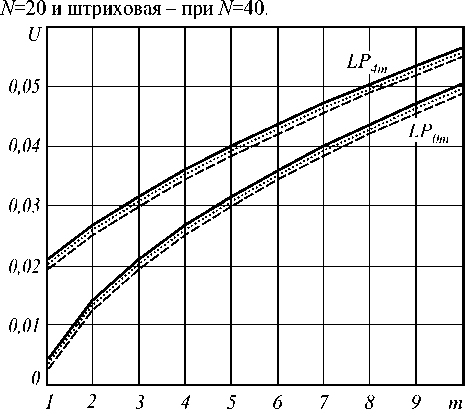
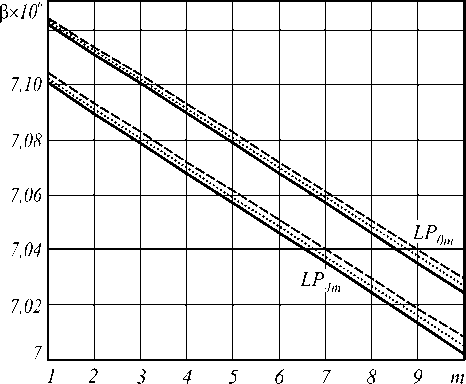
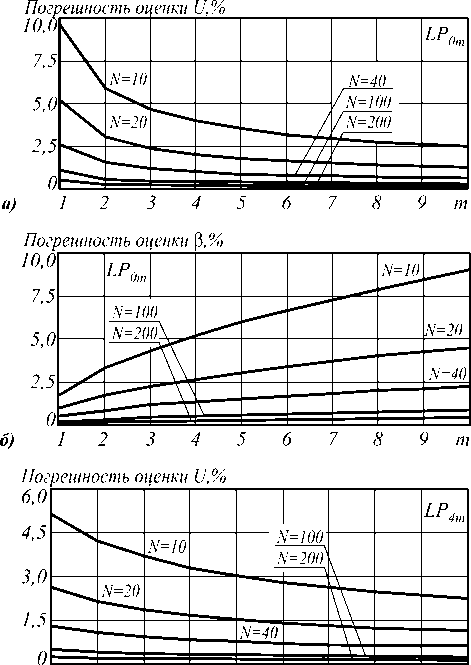
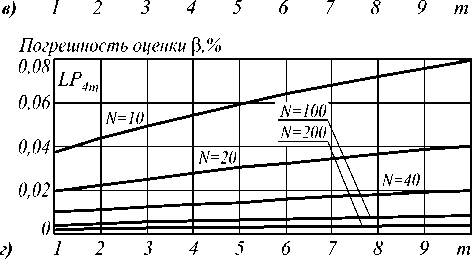
n i N -1 0

N

no - nk где hk = —---— - параметр профиля; nk - показа- n0 - nN тель преломления k-ой оболочки (k=0…N).

После подстановки функции профиля показателя преломления (7) в слагаемое I2 (4) и выполнения соответствующих преобразований с использованием рекуррентных формул относительно степени ортогональных многочленов, формул интегрирования полиномов Лагерра, свойства ортогональности полиномов Лагерра, а также формулы умножения и возведения в степень рядов [5-6], с учетом I1 получим вариационное выражение для параметра моды в сердцевине многомодового волоконного световода с произвольным осесимметричным профилем показателя преломления:

N-1        ^

+V2 E hk exp k=0         в

N-1

- V2 E hk exp k=0

f

-V

U

(m -1)!

(i + m -1)!

+ V exp

^f1

-

V

^J2m-2_n    '(l + q)!

^EDq^E . 2pp )     p=0 ^p !^R 0

R 0 J q 0

+

N-1

+ V2 E hkexp k=0

^fk 2 ^J

_VN²R 02,

x

k²

N2 R <2 J

_x²e²d E'(i+q)! k^2p fkL q^E0 ^qp^E0 p ! N^{2 p}R 0^p V N¹

(k^ mm-D x

N ^R 0 J q=0

_x E^q(1 + q)!(k +1)2^{p f}(k +1)2 p=0 p ! N^{2 p}R 0 ^p

_vN²

- pR 0²l = 0.     (10)

Необходимо отметить, что полученное в результате решения уравнения (10) значение эквивалентного радиуса пятна R0 направляемой моды LPlm справедливо при V>1 и должно удовлетворять условию существования направляемых мод [1, 8 – 9]:

kn1< P < kn₀, (11)

где P - постоянная распространения, которая непосредственно связана с параметром моды в сердцевине и нормированной частотой следующим соотношением [1-9]:

_x²e²d E'(1+q) !k^{2 p} q=0 ^qp=0 p!N^{2 p}R 0 ^p

Р =  /V- a V 2А

- U² .

N-1

V 2 E hk exp k=0

2. Оптическое волокно со ступенчатым профилем показателя преломления

t L

_VN²R 0 ,

_x²E²D E'(i+q)!(k+1)2^p, q^E0   ^Ep ! N^{2 p}R 0^p

Согласно общему алгоритму приближения Гаусса, необходимо найти минимум функции U²(R), при котором аппроксимирующая радиальная зависимость поля моды F_m^(l)(R) будет наиболее близкой к реальному распределению поля моды исследуемого волоконного световода с профилем показателя преломления, описываемого функцией f(R). Для этого необходимо решить следующее уравнение:

U- = о. dR о

В результате дифференцирования (8) с учетом (9) получим характеристическое уравнение, решением которого является значение эквивалентного нормированного радиуса пятна моды LPlm многомодового волоконного световода с произвольным осесимметричным профилем показателя преломления:

f

- M + V² exp

V

J

R 02 J

x

Для оценки погрешности предлагаемого метода

анализа оптических волокон с произвольным осесимметричным профилем показателя преломления рассмотрим два типа профиля волоконных светово-

дов, для которых существует точное решение волнового уравнения: ступенчатый и неограниченный параболический.

Точное решение для ступенчатого профиля пока-

зателя преломления дает радиальную зависимость

поля моды, которая описывается известным выражением вида [1-9]:

Г г i

Ji ^U l

V a J

x

e 2 D:t jl^q^ (1 - pr02)+ q=0    p=0 p'R 02

Fi (r ) =

₍Ji (U)

Ki^fWrl

V a J

Ki (W)

0 < r< a,

a < r < »,

где J_l – функция Бесселя первого рода; K_l – модифицированная функция Бесселя второго рода; W – параметр моды в оболочке.

Расчет параметров передачи направляемых мод волоконного световода со ступенчатым профилем показателя преломления сводится к решению характеристического уравнения, имеющего вид [1-9]:

UJ-+1 (U)= WK+1 (W)

J1 (U)       K- (W) ’

при этом параметры моды в сердцевине U и оболочке W связаны с нормированной частотой V следующим соотношением:

V²= U²+ W². (15) m-й корень характеристического уравнения (14) с учетом (15) определяет параметры направляемой моды LPlm в сердцевине и оболочке, что, в свою очередь, позволяет рассчитать соответствующее значение постоянной распространения в по формуле (12), а также радиуса пятна моды.

Рассмотрим первое и второе определение радиуса пятна моды Петерманна. В первом случае нормированный радиус пятна моды Петерманна-1 определяется по следующей формуле [14]:

R 0 P-1 =

4 Г J о (U)₊£ ₊1      1

3 [ UJ1 (U) 2 W²U²

В свою очередь, нормированный радиус пятна моды Петерманна-2 описывается отношением [14]:

R 0 P-2

J1 (U )У2 WJ о (u ) ■

Достаточно часто погрешность приближенных методов расчета параметров мод волоконных световодов достигает наибольших значений вблизи частоты отсечки, т.е. при значениях V близких к 2,405. На рис. 1 представлены кривые зависимости нормированных радиусов пятна основной моды Петерманна-1 (пунктирная линия) и Петерманна-2 (сплошная линия), а также нормированного эквивалентного радиуса пятна моды (штриховая линия), полученных на основе точных решений и представленного метода при числе оболочек N=10 с учетом коэффициента 2 , связывающего радиусы поля моды Гаусса и ступенчатого световода, соответственно, от нормированной частоты в диапазоне V=1,5…5.

Рис. 1. Зависимость нормированного радиуса пятна моды R0 от нормированной частоты V

Наибольший интерес представляет исследование значений параметра моды в сердцевине U, поскольку данная величина описывает дисперсионные свойства исследуемого волоконного световода с заданным профилем показателя преломления. На рис. 2. приведены кривые зависимости U основной моды LP01 от нормированной частоты, построенные для точных решений (сплошная линия) и значений, полученных на основе модифицированного метода приближения Гаусса (штриховая линия), в диапазоне V=1,5…5.

Рис. 2. Зависимость параметра моды в сердцевине U от нормированной частоты V

Кривые зависимости постоянной распространения основной моды LP01, распространяющейся в сердцевине оптического волокна со ступенчатым профилем показателя преломления, от нормированной частоты в исследуемом диапазоне V=1,5…5, представлены на рис. 3. Сплошная кривая соответ- ствует значениям в, полученным на основе точного

Рис. 3. Зависимость постоянной распространения в от нормированной частоты V

В свою очередь, на рис. 4 приведены графики распределения относительной погрешности расчета параметров передачи основной моды LP01 ступенчатого оптического волокна по значениям нормированной частоты в исследуемом диапазоне V=1,5…5 относительно результатов, полученных на основе точного решения: рис. 4 (а) – параметр моды в сердцевине U, рис. 4 (б) – постоянная распространения β.

б)

Рис. 4. Погрешность предложенного метода: а) параметр моды в сердцевине U;

б) постоянная распространения β

Из рис. 1-4 видно, что максимальная погрешность оценки постоянной распространения β не превышает 0,015% и соответствует минимальному значению нормированной частоты V=1,5 в исследуемом диапазоне. В свою очередь, минимальная погрешность оценки параметра моды в сердцевине U составляет менее 0,8% и соответствует V=2,5. Необходимо отметить, что погрешность оценки U растет в обоих направлениях, как при уменьшении, так и при увеличении нормированной частоты, но не превышает 3% в исследуемом диапазоне V=1,5…5.

Результаты расчета и погрешности оценки параметров передачи, представленные на рис. 1-4, были получены только для основной моды LP01 для наихудшего случая применения приближения Гаусса – анализа волоконного световода со ступенчатым профилем показателя преломления. Очевидно, представляет интерес исследование погрешности расчета характеристик не только моды LP01, но и направляемых мод высших порядков LPlm. Последнее требует перехода из области частоты отсечки к более высоким значениям нормированной частоты V.

Ниже представлены результаты сравнения параметров передачи направляемых мод, распространяющихся в сердцевине многомодового оптического волокна со ступенчатым профилем показателя преломления, полученные при следующих исходных данных: радиус сердцевины a=25 мкм, норми- рованная частота V=24 как на основе точного решения, так и с помощью предложенного метода. В последнем случае анализ волоконного световода указанного типа выполнялся для N=10 оболочек. На рис. 5 представлено распределение значений параметра моды в сердцевине U по радиальному порядку мод m для тех направляемых мод LPlm, у которых величина мощности, переносимой в сердцевине световода, составляет не менее 90%. Сплошная линия соответствует точным значениям, штриховая - ре- зультатам расчета, полученным с помощью пред-

Рис. 5. Распределение значений U высших мод LPlm по радиальному порядку m

Аналогично, на рис. 6 приведены кривые распределения значений постоянной распространения β высших мод по радиальному порядку m.

Рис. 6. Распределение значений β высших мод LPlm по радиальному порядку m

Поскольку характер зависимостей носит одинаковый характер, на рис. 5-6 представлены распределения только для четных значений азимутального порядка l=0, 2, 4. В свою очередь, распределение значений параметров передачи мод нечетных азиму- тальных порядков занимает промежуточное положение между указанными характеристиками.

На рис. 7-8 приведены зависимости погрешности оценки U и в направляемых высших мод от значения радиального порядка моды m. Также исследовались направляемые моды, 90% мощности которых переносится по сердцевине, при 1=0.. .4.

Рис. 7. Распределение значений погрешности оценки U высших мод LPlm по радиальному порядку m

Как видно из рис. 7, максимальные погрешности оценки параметра моды в сердцевине U соответствуют направляемым модам LPl1 (1=0...4; m =1) и не превышают 20% даже для достаточно высокого значения нормированной частоты V=24 при N=10. В свою очередь, максимальная погрешность по в составляет менее 0,08% и соответствует направляемой моде LP17.

дает радиальную зависимость поля моды, которая описывается выражением (1). При этом постоянная распространения в направляемой моды LP_lm определяется по известной формуле [1, 8-9, 15]:

в = kn₀ 1 - ²^И-[2(m -1)+1 +1]. (18) akn₀

Соответственно, параметр моды в сердцевине U можно рассчитать, используя выражение (12), предварительно преобразованного к следующему виду:

ГТ

U = V— - а²в² . (19) 2А

В общем случае предполагается, что в идеальном неограниченном параболическом профиле показателя преломления, который описывается соответствующей функцией профиля f(R)=R2, отсутствует оболочка. В соответствии с вышесказанным, вариационное выражение для параметра моды в сердцевине (8) и характеристическое уравнение (10) примут следующий вид:

U2

(m -1)! j M

(1 + m -1)! [ R₀²

• ²    »    2 m-2    l+q

+VT 2 k²2 Dq 2 ⁽l + q) ^!_2p N²k0 q=0 qp0 p ! N^{2 p}R₀^{2 p}

X

X

( k² J , k^2p expl--—1-(k +1)^2p

( N²R 0 J

(k +1)2J' N²R 0 ^J

I (20)

^ 0,08

Рис. 8. Распределение значений погрешности оценки в высших мод LPlm по радиальному порядку m

v² ” i (

- M +—- 2 k2 exp

N²k=0 I

k²

—

N²R о J

_x 22²_D 2'(i+q) ^!k^{2 p} (k² q=0 qp=0p!N^2pR₀^2p IN¹

V²^       (

- NF k2k 4

(kit)! J N²R₀^{2 J}

X

²m-²_D 2’(1 + q)!(k +1)^2p q=0 qp=0 p ! N^{2 p}R₀^{2 p}

-

pR0²

-

((k +1)²

( N²

- pR 0²| = 0.(21)

3. Оптическое волокно с идеальным неограниченным параболическим профилем показателя преломления

Точное решение волнового уравнения для волоконного световода с идеальным неограниченным параболическим профилем показателя преломления

Для оценки погрешности разработанного метода при анализе оптических волокон со сглаженным профилем выполним сравнение результатов расчета параметров передачи направляемых мод, распространяющихся по волоконному световоду с неограниченным параболическим профилем показателя преломления, полученных на основе точного решения и с помощью предложенного метода, который базируется на модифицированном методе приближения Гаусса. По аналогии с предыдущим разделом,

предварительно выполним исследование в области частоты отсечки, а именно в диапазоне нормированных частот V=1,5…5.

На рис. 9 представлены графики зависимости параметра основной моды в сердцевине U от нормированной частоты V. Сплошная кривая соответствует точному решению, штрих пунктирная – значениям U, полученным с помощью разработанного метода при числе оболочек N=10, штриховая – при N=20 и

Рис. 9. Зависимость параметра моды в сердцевине U от нормированной частоты V

Аналогично, кривые зависимости постоянной распространения β основной моды LP01 волоконного световода с неограниченным параболическим профилем показателя преломления от нормированной частоты, изменяющейся в исследуемом диапазоне

Рис.10. Зависимость постоянной распространения β от нормированной частоты V

На рис. 11 и 12 приведены графики зависимости погрешности оценки параметров передачи основной моды, полученные с помощью предложенного метода на основе модифицированного метода приближения Гаусса, относительно точного решения для волоконного световода с неограниченным парабо- лическим профилем показателя преломления для разных значений N=10…200 в исследуемом диапазоне нормированной частоты V=1,5…5.

Рис. 11 соответствует указанной зависимости погрешности оценки параметра основной моды в сердцевине U в диапазоне V=1,5…5 для N=10…200.

для разных значений N

для разных значений N

Рис. 12 соответствует распределению значений относительной погрешности оценки постоянной распространения β основной моды LP01 оптического волокна с неограниченным параболическим профилем показателя преломления, оценка которой выполнена при вышеуказанных условиях.

Согласно рис. 11-12, чем больше значение нормированной частоты V, тем больше требуется точек, воспроизводящих профиль исследуемого световода, для уменьшения погрешности оценки параметров передачи направляемых мод. Так, погрешность оценки U составляет менее 1% при N=40 на частоте отсечки. В то же время при N=100 максимальное значение погрешности оценки U не превышает 0,5% во всем исследуемом диапазоне V. Максимальная погрешность оценки β составляет менее 0,07% даже при N=10.

На рис. 13 – 14 представлены результаты расчета параметров передачи направляемых мод, распространяющихся в сердцевине многомодового оптического волокна с неограниченным параболическим профилем показателя преломления, полученные при следующих исходных данных: радиус сердцевины a=25 мкм, нормированная частота V=24 как на основе точного решения, так и с помощью разработанного метода. Кривые распределения U по радиальному порядку направляемых мод LPlm (l=0 и 4; m=1…10) приведены на рис. 13. Сплошная линия соответствует точному решению, пунктирная – приближенному при

Рис. 13. Распределение значений U высших мод LPlm по радиальному порядку m

Рис. 14. Распределение значений β высших мод LPlm по радиальному порядку m

Графики распределения значений постоянной распространения β направляемых мод многомодового оптического волокна с неограниченным параболическим профилем показателя преломления, построенные при указанных условиях, представлены на рис. 14.

Также на рис. 15 приведены кривые распределения относительной погрешности оценки параметров передачи высших мод, распространяющихся в опти- ческом волокне исследуемого типа и тех же характеристиках (a=25 мкм и V=24), по радиальному порядку m для следующих значений N=10, 20, 40, 100 и 200. Рис. 15 (а, в) соответствует погрешности оценки параметра моды в сердцевине U направляемых мод высших порядков LP0m (рис. 15 (а) и LP4m (рис. 15 (в). Следует отметить, что графики распределения погрешности U направляемых мод LP1m, LP2m, LP3m имеют аналогичный характер и занимают промежуточное положение между кривыми, соответствующими LP0m и LP4m, при одинаковых N.

Рис. 15. Распределение значений погрешности оценки параметров передачи высших мод LP_lm по радиальному порядку m

В свою очередь, рис. 15 (б, г) соответствует графикам распределения значений погрешности оценки постоянной распространения β высших мод по радиальному порядку m при аналогичных условиях. Как видно из рис. 15, наиболее высокие значения погрешности оценки U соответствует модам LP0m, од- нако указанная величина не превышает 10% даже при N=10. Для уменьшения погрешности по U до 1% и менее требуется N>100 для описания профиля световода с более высоким значением радиуса сердцевины a=25 мкм при V=24, по сравнению с геометрическими параметрами оптических волокон, характеризуемых нормированной частотой V=1,5…5. Одновременно максимальная погрешность по β составляет менее 0,1% вне зависимости от числа оболочек N.

Заключение

Предложен метод анализа многомодовых волоконных световодов с произвольным осесимметричным профилем показателя преломления. Данный метод является обобщением модифицированного метода приближения Гаусса на рассматриваемый случай и позволяет рассчитать параметры передачи направляемых мод произвольного порядка, распространяющихся в многомодовых оптических волокнах с произвольным осесимметричным профилем показателя преломления. В отличие от известных решений на основе приближения Гаусса исследуемое волокно рассматривается как волоконный световод с многослойным профилем показателя преломления. При этом профиль показателя преломления сердцевины представляется в виде конечного числа N оболочек, в пределах которых значение показателя преломления остается постоянным. Это позволяет записать вариационное выражение для параметра моды в сердцевине U и характеристическое уравнение, решением которого является эквивалентный нормированный радиус пятна моды R₀ , в виде конечных вложенных сумм, что существенно сокращает время вычислений даже при расчете параметров передачи мод высших порядков.

Представлены результаты оценки погрешности предлагаемого метода, выполненной путем сравнения значений параметров передачи, как основной моды, так и направляемых мод высших порядков, полученных на основе точных решений и с помощью указанного метода на основе модифицированного приближения Гаусса. В частности, расчет выполнялся для постоянной распространения β и параметра моды в сердцевине U направляемых мод LP_lm оптических волокон со ступенчатым и неограниченным параболическим профилями показателя преломления, для которых существует точное решение волнового уравнения.

Исследования погрешности выполнялись как для основной моды в области частоты отсечки, при этом значения нормированной частоты выбирались в диапазоне V=1,5…5, так и для мод высших порядков при сравнительно высоких значениях V=24, соответствующих типовым многомодовым оптическим волокнам 50/125. Показано, что при анализе градиентных волоконных световодов с увеличением значения нормированной частоты V требуется повышение количества оболочек N, воспроизводящих фор- му профиля показателя преломления исследуемого волокна. Анализ полученных результатов продемонстрировал приемлемую точность предложенного метода, что позволяет достаточно эффективно использовать его в задачах расчета параметров передачи направляемых мод произвольного порядка, распространяющихся в оптических волокнах с осесимметричным профилем показателя преломления сложной формы.