Анализ моделей эволюции пористости при паротепловом воздействии на продуктивный пласт

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2019PNRPU MECHANICS BULLETIN

В настоящее время нефтедобывающая промышленность сталкивается с проблемой активного истощения большинства месторождений традиционного углеводородного сырья. Поддержание и увеличение достигнутых темпов добычи может быть осуществлено путем интенсивного вовлечения в разработку запасов тяжелой нефти и природных битумов, потенциальные ресурсы которых превышают традиционные залежи [1–4]. Основной особенностью данного вида углеводородов является их малая подвижность, обусловленная высокой вязкостью. По этой причине высокие показатели нефтеотдачи могут быть достигнуты только путем проведения специальных геолого-технических мероприятий [5, 6].

Одной из наиболее эффективных технологий разработки залежей сверхвязких нефтей является парогравитационное дренирование (ПГД) [7, 8]. Данный метод предполагает бурение двух параллельных горизонтальных скважин, расположенных друг над другом. Верхняя скважина используется для нагнетания перегретого пара в продуктивный пласт с целью создания и развития паровой камеры с температурой выше температуры парообразования. По мере повышения температуры в пласте подвижность нефти увеличивается, и она под действием гравитации стекает к нижней добывающей скважине вместе с пластовой водой и конденсированным паром.

Рост паровой камеры обусловлен повышенным поровым давлением и теплообменом между продуктив- ным пластом и закачиваемым горячим паром, включающим в себя процессы теплопроводности, конвективного теплопереноса и выделения скрытой теплоты фазового перехода. Происходящее при этом изменение напряженно-деформированного состояния продуктивного пласта может приводить к разрушению кровли [1, 9–11], срезу обсадных колон нагнетательной и добывающей скважин [12] и изменению его фильтрационноемкостных характеристик.

В работе [1] отмечается, что при высоком давлении нагнетания может возникнуть вертикальный разлом, распространение которого приводит к нарушению целостности кровли и прорыву пара в верхние слои. Другим геомеханическим эффектом является сжатие пористого скелета кровли в результате теплового воздействия, что грозит падением горизонтального напряжения и как следствие возникновением вертикального гидроразрыва. В работах [9–11] проводится численное моделирование процесса ПГД с целью исследования прочности кровли продуктивного пласта на основе критериев Мора–Кулона и Друкера–Прагера с учетом анизотропии механических свойств. В работе [13] на основе термопороупругости показано, что воздействие высоких температур приводит к увеличению сжимающих напряжений, что может вызывать разрушение обсадных колон скважин. Исследованию влияния на устойчивость обсадных колон сжимающих и сдвиговых напряжений, возникающих при повышении давления и температуры, посвящены работы [14, 15]. В работе [16]

отмечается, что одной из основных причин возникновения повреждений обсадных колон в ходе ПГД является ползучесть околоскважинного пространства пласта.

Обширные экспериментальные исследования показывают, что существенное влияние на прочностные и деформационные характеристики горной породы оказывает наличие в ней пор и характер их распределения [17, 18]. В ходе технологического процесса ПГД изменение пористости происходит вследствие различных механизмов, связанных с увеличением температуры и порового давления. В работе [19] на основе данных мониторинга процесса ПГД, проведенного с использованием радиолокационной интерферометрии, было установлено, что при высоких давлениях нагнетания пара возникает сдвиговая дилатансия, которая существенно увеличивает как пористость, так и проницаемость продуктивного пласта. В работах [20–22] этот эффект был исследован на основе численного моделирования. В свою очередь, в работе [12] отмечается, что при высоком поровом давлении нагрев может привести к уменьшению пористости и проницаемости вследствие расширения зерен породного скелета. В работе [23] с использованием численного моделирования показано, что отказ от учета геомеханических эффектов приводит к некорректной оценке нефтеотдачи.

Для описания нефтедобычи методом ПГД используются аналитические и численные модели. В работе [24] на основании закона Дарси и законов сохранения массы и энергии было получено одно из первых аналитических соотношений для расчета дебита добывающей скважины. Дальнейшее развитие этого подхода связано с учетом дополнительных факторов, таких как форма паровой камеры и отток тепла в кровлю продуктивного пласта [25, 26], нестационарность теплообмена на границе паровой камеры [27], предельного градиента давления, достижение которого необходимо для течения сверхвязкой нефти [28]. Несмотря на значительный прогресс в развитии аналитических моделей, они не позволяют в полной мере описать конвективный тепло-перенос и фазовый переход, возникающий при конденсации пара и испарении воды, а также не учитывают геомеханические эффекты. По этой причине для описания сложного взаимодействия физических процессов при ПГД широкое распространение получило численное моделирование. Большинство моделей нефтедобычи с использованием паротеплового воздействия включают в себя закон сохранения массы для трехфазного потока, закон сохранения энергии и уравнение равновесия [29–31]. Влияние порового давления и температуры на механические напряжения описывается с использованием теорий Био и термоупругости. В то же время существует большое разнообразие в выборе определяющих соотношений для описания изменения пористости [32].

В наиболее простой модели пористость линейно зависит от порового давления с коэффициентом пропор- циональности, равным коэффициенту поровой сжимаемости [21, 33]. В [34, 35] с использованием теории гидростатической пороупругости в предположении изменения объемов породного скелета и порового пространства была получена зависимость пористости от средних напряжений в приращениях с коэффициентом, линейно зависящим от текущего значения пористости. При малой сжимаемости породного скелета пористость может быть связана со средними эффективными напряжениями через композицию дробно-линейной функции и экспоненты [36]. В работе [37] на основе лабораторных экспериментов по сжатию песчаника была предложена другая экспоненциальная зависимость пористости от средних эффективных напряжений. В [38, 39] на основе теории Био и теоремы Бетти приращение пористости было выражено через линейную комбинацию приращений объемных деформаций и порового давления. В модификации этого соотношения для случая малой сжимаемости породного скелета зависимость между пористостью и объемными деформациями устанавливается также через экспоненту [40, 41]. В то же время в работах [31, 42, 43] предложена дробно-линейная зависимость пористости от объемных деформаций.

Проведенный анализ литературы показывает, что выделяют три основных параметра, влияющих на эволюцию пористости: изменение порового давления, объемных деформаций и эффективных напряжений. Данная работа посвящена анализу ключевых моделей пористости применительно к ПГД, поскольку сложность и физическая связанность протекающих при этом процессов может приводить к принципиально различным результатам. Для описания ПГД была разработана модель, которая включает в себя уравнения баланса массы для трехфазной жидкости, закон сохранения энергии с учетом фазового перехода, возникающего при испарении пара и конденсации воды, а также закон Дарси для описания фильтрационного течения [44].

1.    Связанная термогидромеханическая модель фильтрации многофазной жидкости в пористой среде

Описание всего многообразия явлений, возникающих при парогравитационном дренировании, является достаточно сложной задачей. Тепло- и массоперенос в деформируемой пористой среде характеризуется взаимодействием температурных, механических и гидродинамических процессов и трех различных фаз (твердой, жидкой и газообразной). В связи с этим в работе принимаются следующие гипотезы:

• •    флюид, заполняющий поровое пространство, состоит из трех различных несмешиваемых компонентов (вода, пар, нефть);

• •    фазовый переход обусловлен только температурными изменениями;

• •    вследствие высокой пористости пород-коллекторов влияние капиллярного давления не учитывается;

  • •    течение каждой из составляющих флюида подчиняется закону Дарси;

  • •    продуктивный пласт изотропен, а его деформации малы.

  Уравнения, используемые для описания связанных термогидромеханических процессов, условно можно разделить на две группы: законы сохранения массы, энергии, момента импульса и определяющие соотношения (уравнения состояния), к которым относятся законы Дарси, Фурье, Гука и т.д.

  Таким образом, математическое описание процесса парогравитационного дренирования с учетом принятых выше гипотез включает в себя:

  • •    уравнение баланса массы воды

  d( n Р wSw) , vm

  ----т + V'(p wvw ) = qw;(1)

  о t

  • •    уравнение баланса массы пара

  d ( n Р, S )

  ( X s) + V-(ps Vs ) = qs;(2)

  о t

  • •    уравнение баланса массы нефти

  d np p„ S„),

  ( X o) + V-(poVo) = 0;(3)

  d t

  • •    замыкающее соотношение

  Sw+Ss+So = 1;(4)

  
  

  о = C : ( £ -а _т ( T - T o ) E ) -a _Bp E ;       (10)

  
  

  • геометрическое соотношение для описания

  
  

  линейного тензора полной деформации

  
  

  £ = 12 ( V u + V u ^T ) .              (11)

  
  

  • уравнение баланса энергии с учетом конвективного теплопереноса и фазового перехода, вызванного испарением и конденсацией воды

  
  
  
  
  

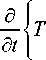
  (1 - n ) p rCr + n £ p i S i c i i = w , o , s

  
  
  

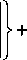
  + V . ( -X f V T ) + V v , . V ( p ,. S ,. c ,. nT ) = Q ;

  i = w , o , s

  
  
  
  

  • закон Дарси для описания фильтрации каждого из компонентов:

  
  

  v w = - Kk rw ( V p - p w g ) ;	(6)
  Ц w
  v s = - Kk rs- ( V p - p s g ) ; Ц s	(7)
  v o = - Kk ro - ( V p - p o g ) ; Ц o	(8)

  
  

  В уравнениях (1)-(11): n - пористость; S_w , S s , S o -водонасыщенность, паронасыщенность, нефтенасы-щенность (отношение части порового объема, занимаемой фазой, к общему объему пор); t - время; V - оператор Гамильтона; v _w , v s , v _o - скорости фильтрации воды, пара и нефти; q_w , q_s - массовые источники, вызванные фазовым переходом; p - поровое давление; g - ускорение свободного падения; k rw , k_rs , k_ro - относительные проницаемости для воды, пара и нефти; ц _w , ц s , ц _o - динамические вязкости воды, пара и нефти; T - абсолютная температура; Q - тепловой источник, вызванный фазовым переходом; p _w , p s , p _o , p _r -плотности воды, пара, нефти и частиц грунта; p - эффективная плотность, p = ( 1 - n ) p _r + nS_s p _s + nS w p _w + + nS_o p _o ; c w , c s , c o , c_r - удельные теплоемкости воды, пара, нефти и частиц грунта; X _w , X s , X _o , X _r - коэффициенты теплопроводности воды, пара, нефти и частиц грунта; X ef - эффективный коэффициент теплопроводности, X f = ( 1 - n ) X r + n X s S s + n X w S w + n X o S o ; K - абсолютная проницаемость продуктивного пласта; о -тензор напряжений; C - тензор упругих постоянных, который в случае применения изотропной линейной теории упругости сводится к двум упругим постоянным (модулю всестороннего сжатия и модулю сдвига); £ -тензор малых деформаций; а _т - коэффициент теплового расширения грунта; T ₀ - начальное значение температуры; a _B - коэффициент Био; E - единичный тензор; u - вектор перемещений.

  Для определения относительных проницаемостей использовались следующие соотношения [45]:

  
  

  k_rw

  
  

  m

  f S - S 1 ¹

  w rw

  ^а 1 I     _{с с} I , S rw <  S w — 1,

  1 ^{1 -} S rw ^- S ro J

  0, S w — S rw ,

  
  
  
  

  • уравнение равновесия

  
  

  k rs

  
  

  a ₂

  
  

  I      S s - S rs

  l ^{1 - S}rs ^{- S}rw ^{- S}ro

  
  

  , S rs <  S s — 1,

  
  
  
  

  V. о + p g = 0 ;                   (9)

  
  

  0, S s — S rs ,

  
  

  • определяющее соотношение для описания механического поведения пористой среды с учетом температурного расширения частиц грунта и влияния порового давления

  
  

  к - < ^{a 3}

  k ro = 1

  
  

  S o

  
  

  - ^Sro

  
  

  ^{1 - S}ro ^{- S}rw

  
  

  0, S o — S ro ,

  
  

  m 3

  I , S ro <  S o — 1,

  
  
  
  

где a ₁ , a ₂ , a ₃ , m ₁ , m ₂ , m ₃ – эмпирические параметры; S_rw , S_rs , S_ro – остаточные значения водо-, паро- и неф-тенасыщенности.

Источники, появляющиеся в уравнениях (1), (2), (5) вследствие фазовых переходов, вызывающих испарение и конденсацию воды, имеют вид [46]

Q = Lq w ,                   (15)

Q s = ^- Q w = i

„ T-T. „ „ rnSs p-----sat-, T < T ss             s

T sat

T - T . _ _ rnS w P w-^pa- , T >  T sa, , T sat

где L – скрытая теплота парообразования; r – эмпирический параметр, характеризующий скорость фазового перехода; T_sat – температура фазового перехода.

Для описания изменения пористости горных пород разрабатываются различные модели, которые, как правило, сводятся к установлению взаимосвязи между пористостью и следующими параметрами: объемные деформации, поровое давление или эффективное напряжение. В данной работе анализируются некоторые ключевые модели, приведенные ниже.

Одним из общепринятых соотношений, связывающим пористость с поровым давлением флюида, является [33]

n = n 0 ( 1 + C r ( p ^- p 0 ) ) , ⁽¹⁷⁾

где n ₀ – начальная пористость; c_r – сжимаемость горной породы; p ₀ – начальное давление.

Для учета изменения пористости, вызванного влиянием объемной деформации и порового давления, Y. Wang и B. Lu [39] использовали следующее уравнение:

dn = ( a B - n )( d £ vol + c_rdp ) .            (18)

Появление объемной деформации вызывает изменение пористости, которое определяется согласно соотношению [40]

n = ^{1 -} ( 1 ^- n о ) Exp [ ^-£ vol ] ,

где £ vol - объемные деформации.

Для одновременного учета порового давления и механических напряжений применяют уравнение [35]

dn = - ( c_p ( 1 - n ) - c_r ) d ст ',             (20)

где    c _p   - сжимаемость пор; ст ' = ст m -a B p ;

ст = -(ст + ст + ст )/3.

m           xx yy zz .

На основе лабораторных экспериментов в работе [37] было предложено соотношение для связи пористости с эффективными напряжениями n = nr +(n 0 - nr) Exp [-a ст'],            (21)

где n_r – остаточная пористость; a – эмпирический параметр.

В предположении постоянства объема частиц грунта может быть также получена следующая формула [36]:

n = n ₀

Exp [ ^- c p ^ст ' ]

^{1 - n} 0 ( 1 ^{- E} xp [ ^- c p ^ст ' ] )

Система уравнений (1)–(11) дополнялась начальными и граничными условиями:

p ( t = 0 ) = p 0 , T ( t = 0 ) = T 0 ,	(23) (24)
S w ( t = 0 ) = s w ,	(25)
S s ( t = 0 ) = 0,	(26)
Sw | Г , = Srw ,	(27)
S s |г, = 1 - S rw - S ro ,	(28)
p Г , = p b ,	(29)
p Г 2 = p w ,	(30)
T |г, = T b ,	(31)
- n ■ q ' г 2 = 0,	(32)
- n ■ ( P s v s ) Г 2 =- n ■ ( P s v s ) ,	(33)
- n ■ ( P w v w ) Г 2 =- n ■ ( P w v w ) ,	(34)
p m Г , = p b ,	(35)
pm Г 2 = p w ,	(36)
ux Г з, Г 4 = 0 ,	(37)
u y РГ6 = 0 ,	(38)

где p ₀ – начальное значение давления; T ₀ – начальное значение температуры; S _w ⁰ – начальная водонасыщен-ность; Г 1 - граница нагнетающей скважины; p b - давление нагнетаемого пара; Г ₂ - граница добывающей скважины; p_w – давление в добывающей скважине; n – вектор нормали; q ' - вектор теплового потока; Г ₃, Г 4 -правая и левая границы расчетной области; Г ₅, Г 6 -верхняя и нижняя границы расчетной области.

Таким образом, замкнутая система уравнений для описания парогравитационного дренирования включает уравнения (1)–(11), выражения (12)–(16), одно из соотношений (17)–(22), а также начальные и граничные условия (23)–(38).

2. Численная реализация модели

т I           V' с   I ^{d n}

⁺ T 1 ^—p r c r ⁺ E ^P i S i c i ГЕ7 +

I у                i = { w , o , s }             7 ^d t

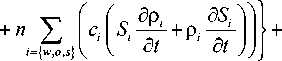
Для решения системы уравнений был разработан численный алгоритм [44], основные этапы которого приведены ниже:

• преобразование уравнений (1)-(4), (6)-(8) с использованием общей скорости потока v = E v_t :

i = { w , o ,s }

+ T 1 E v i - ( S i C i n Vp i + C i n P i V S i + S i C i P i V n ) ^ = Q ; (44) I i = { w , o , s }                                                                                        I

v = - K XV p + K g E X i P i ,         (39)

i = { w , o ,s }

• решение уравнений методом конечных элементов в пакете Comsol Multiphysics® с использованием следующих модулей: Weak Form PDE Interface для (42), (43), Heat Transfer для (44), Structural Mechanics (9)–(11). Для дискретизации по времени использовалась неявная схема Эйлера первого порядка.

^V- v =^-d n + E "1 I q i ^{- v}i -^V Pi ^- nS i ^J, ⁽⁴⁰⁾

O t i = { w , o ,s } ^р i у                            О t )

8 Sj „ n—- + V- v, dt          1

_c 8 n   1

^— Si^ -L

q j

—

„ ⁵P, ^nS1lT ^— v .vP 1 , (41)

3. Результаты численного моделирования эволюции пористости в процессе парогравитационного дренирования

где X = E X i ; X i. = k_ri I P i ; j = { w ,s } ;

i = { w , o ,s }

• •    запись уравнений (39)-(41) в слабой форме при помощи умножения на тестовую функцию и применения формулы интегрирования по частям;

• •    добавление к каждому из уравнений слагаемого с искусственной диффузией для стабилизации осцилляций численного решения:

" JJJ v - ^V p dV =

V

qi

dp. I

— v, -Vp,.— nS -^P i i                 i 8 t JI

x pdV — JJJ c a V v - V pdV ,            (42)

V

[ n S+у E1 Sdr — ff   x jj

V V t          t 7             V ^P 1

Трехмерное моделирование паротеплового воздействия на нефтяной коллектор проводилось для прямоугольной области, имеющей следующие размеры: толщина 5 м, высота 24 м, ширина 30 м. Добывающая скважина располагалась на расстоянии 10 м от подошвы пласта, нагнетающая – на 5 м выше. Скважины имели диаметр 0,178 м. Начальные и граничные условия, используемые при моделировании, даны в табл. 1. Физико-механические свойства продуктивного пласта, нефти, воды и пара представлены в табл. 2, 3. Зависимость динамической вязкости нефти от температуры изображена на рис. 1 [47].

Расчетная область разбивалась на тетраэдральные конечные элементы, общее число которых составляло 11 142. Размер элементов варьировался от минимального (вблизи скважины), равного 0,09 м, до максимального (на периферии), равного 1 м.

Таблица 1

Начальные и граничные условия

^x I q j ^{— n} S ^^^—v i ^-Vp i I S j ^— JJJ v ^j '^V S j ⁺

V            ^d t             7 V

+ JJJ S aj V ^Si' V S ^i dV = 0,             (43)

V

где j = { w ,s } , p , S i w , S i _а - тестовые функции; c_Q , S_a w , S_a – параметры искусственной диффузии;

• преобразование уравнения (5) к виду

^{(1 — n} ) P r c r ^{+ n} E P i S i c i i = { w , o , s }

d T

— + dt

+

E  piSicinvi i={ w, o, s }

-V T + V- ( —X eff V T ) +

Table 1

Initial and boundary conditions

Свойство	Символ	Значение	Размерность
Начальное значение нефтенасыщенности	So 0	0,88
Начальное значение водонасыщенности	S w 0	0,12
Начальная температура продуктивного пласта	T 0	281,15	К
Температура закачиваемого пара	T b	496	К
Начальное значение давления	P 0	2·106	Па
Давление закачиваемого пара	P b	3,575·106	Па
Давление в добывающей скважине	P w	1,7·106	Па

Таблица 2

Механические свойства

Mechanical properties

Table 2

Свойство	Символ	Значение	Размерность
Модуль Юнга	E	3·109	Па
Коэффициент Пуассона	ν	0,25
Коэффициент теплового расширения грунта	α т	5·10–6	1/К
Коэффициент Био	α B	0,44

Таблица 3

Теплофизические свойства

Thermophysical properties

Table 3

Свойство	Символ	Значение	Размерность
Абсолютная проницаемость продуктивного пласта	K	2,68·10–12	м2
Вязкость воды	µ w	1004·10–6	Па∙с
Вязкость пара	µ s	16·10–6	Па∙с
Остаточная нефтенасыщенность	S ro	0,68
Остаточная водонасыщенность	rw	0,0
Остаточная паронасыщенность	S rs	0,0
Плотность нефти	ρ o	933	кг/м3
Плотность воды	ρ w	1012	кг/м3
Плотность скелета	ρ r	2100	кг/м3
Плотность пара	ρ s	0,3	кг/ м3
Теплопроводность нефти	λ o	0,14	Вт/(м∙К)
Теплопроводность воды	λ w	0,58	Вт/(м∙К)
Теплопроводность пара	λ s	23·10–2	Вт/(м∙К)
Теплопроводность скелета	λ r	2,325	Вт/(м∙К)
Теплоемкость нефти	c o	2090	Дж/(кг∙К)
Теплоемкость пара	c s	2000	Дж/(кг∙К)
Теплоемкость воды	c w	4200	Дж/(кг∙К)
Теплоемкость скелета	c r	1050	Дж/(кг∙К)
Пористость	n	0,27
Эмпирический параметр	a 1	75·10–2
Эмпирический параметр	a 2	40·10–3
Эмпирический параметр	a 3	12·10–3
Эмпирический параметр	m 1	3,45
Эмпирический параметр	m 2	3
Эмпирический параметр	m 3	2,1

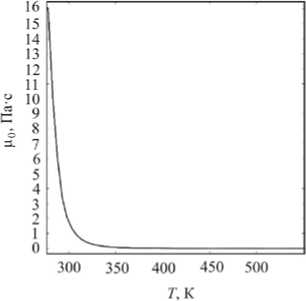
Рис. 1. Зависимость динамической вязкости нефти от температуры [47]

Fig. 1. Dynamic viscosity of oil versus temperature [47]

На рис. 2–17 представлены результаты расчетов основных параметров, характеризующих процесс ПГД, согласно разработанной модели (1)–(16) и соотношений (17)–(22). На рис. 3, 4, 8, 9, 13, 14 показаны характерные распределения паро- и нефтенасыщенностей. Максимальная скорость распространения пара сосредоточена внутри паровой камеры. Значение нефтенасыщенности в паровой камере совпадает с остаточным. Нефть за пределами паровой камеры является неподвижной вследствие высокой вязкости.

Результаты расчетов пористости согласно формулам (17)–(22) показали, что существует три качественно различных картины ее распределения по расчетной области.

На рис. 2–6 показаны результаты, полученные согласно модели (18). В этом случае распределение пористости (рис. 5) определяется слагаемым, зависящим от порового давления (рис. 6), несмотря на присутствие в формуле объемной деформации. Аналогичный результат можно получить с использованием модели (17).

Второй характерный вид представлен на рис. 7–11. В этом случае пористость (рис. 10) рассчитывалась согласно (19), и ее вид соответствует распределению объемной деформации (рис. 11).

К третьему типу, показанному на рис. 12–16, относятся соотношения (20)–(22). На рис. 15 представлено распределение пористости, полученное согласно модели (21). Особенностью таких моделей является зависимость от эффективных механических напряжений, вид которых представлен на рис. 16. На рис. 15, 16 можно наблюдать образование «кольца», соответствующего фронту фазового перехода. В его пределах возникает повышенное уплотнение грунта. На начальном этапе ПГД в области, соответствующей паровой камере, происходит увеличение пористости вследствие влияния порового давления (рис. 15, а ). В дальнейшем уплотнение грунта приводит к уменьшению порового давления и росту эффективных сжимающих напряжений (рис. 16, б , в ), в результате вся расчетная область находится в состоянии сжатия (рис. 15, б , в ).

Модели пористости по-разному влияют на основные параметры, характеризующие ПГД, что может приводить к разным оценкам дебита нефти. При использовании формулы (19) паровая камера имеет минимальный размер. Соответствующие ей величины нефтенасыщенности и температуры приведены на рис. 7 и 9. Использование модели (21) приводит к повышению скорости ПГД (рис. 12–14). В этом случае паровая камера к 100-му дню достигает кровли пласта, что соответствует переходу от начального этапа роста паровой камеры ко второму этапу, связанному с расширением паровой камеры в горизонтальном направлении. Наиболее быстрый процесс ПГД наблюдается при использовании формулы (18) (рис. 2–4). Результаты показывают, что уже на 60-й день паровая камера распространяется вдоль кровли пласта более чем наполовину.

а                               б                               в

Рис. 2. Распределение температуры по расчетной области, полученное при использовании модели пористости (18): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 2. Evolution of temperature field obtained with the use of porosity model (18) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

а                               б                               в

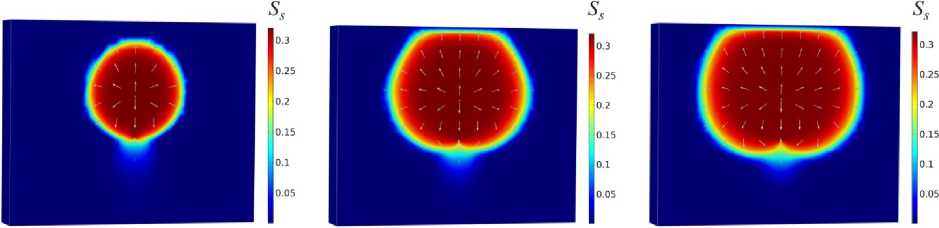
Рис. 3. Распределение паронасыщенности совместно с наложенным полем скорости по расчетной области, полученное при использовании модели пористости (18): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 3. Evolution of steam saturation together with the velocity field obtained with the use of porosity model (18)

for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

а                               б                               в

Рис. 4. Распределение нефтенасыщенности по расчетной области, полученное при использовании модели пористости (18): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 4. Evolution of oil saturation obtained with the use of porosity model (18) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

An                          An                          An

а                               б                               в

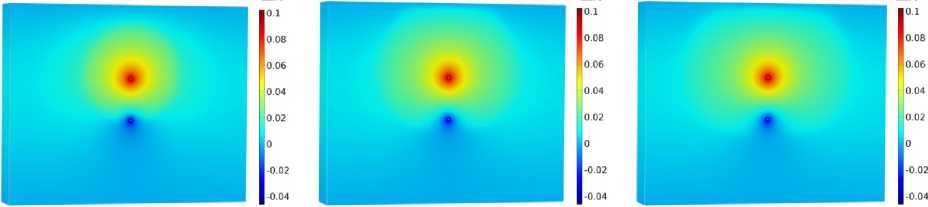
Рис. 5. Распределение изменения пористости по расчетной области, полученное при использовании модели пористости (18): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 5. Evolution of porosity change obtained with the use of porosity model (18) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

а                                 б                                 в

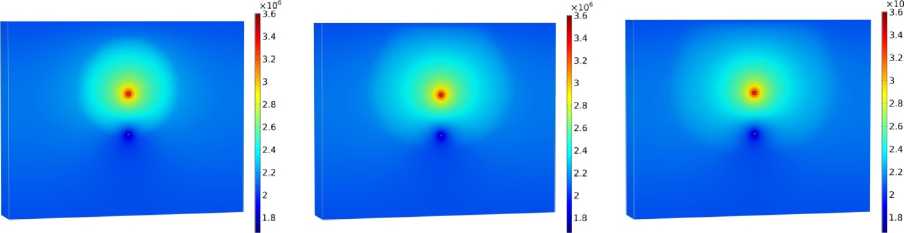
Рис. 6. Распределение порового давления по расчетной области, полученное при использовании модели пористости (18): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 6. Evolution of pore pressure obtained with the use of porosity model (18) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

а

б

в

Рис. 7. Распределение температуры по расчетной области, полученное при использовании модели пористости (19): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 7. Evolution of temperature field obtained with the use of porosity model (19) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

а                              б                               в

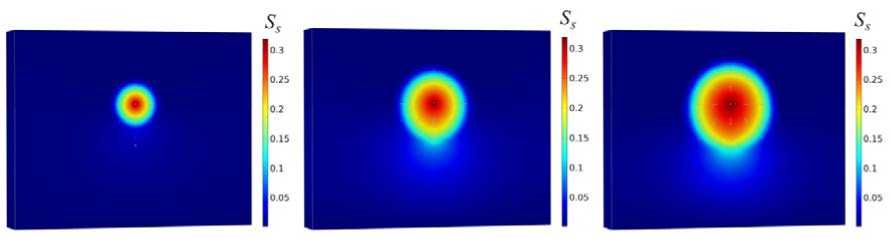
Рис. 8. Распределение паронасыщенности совместно с наложенным полем скорости по расчетной области, полученное при использовании модели пористости (19): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 8. Evolution of steam saturation together with the velocity field obtained with the use of porosity model (19) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

а                                 б                                 в

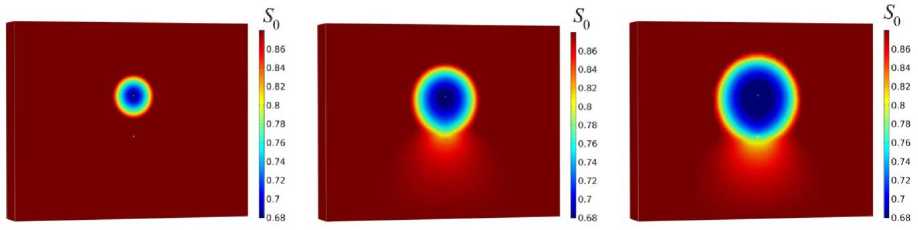
Рис. 9. Распределение нефтенасыщенности по расчетной области, полученное при использовании модели пористости (19): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 9. Evolution of oil saturation obtained with the use of porosity model (19) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

б

а

в

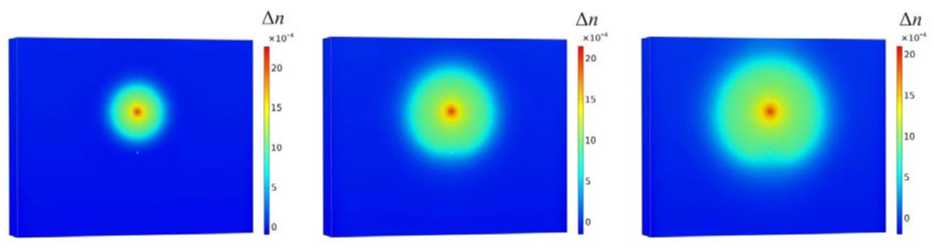
Рис. 10. Распределение изменения пористости по расчетной области, полученное при использовании модели пористости (19): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 10. Evolution of porosity change obtained with the use of porosity model (19) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

а                               б                               в

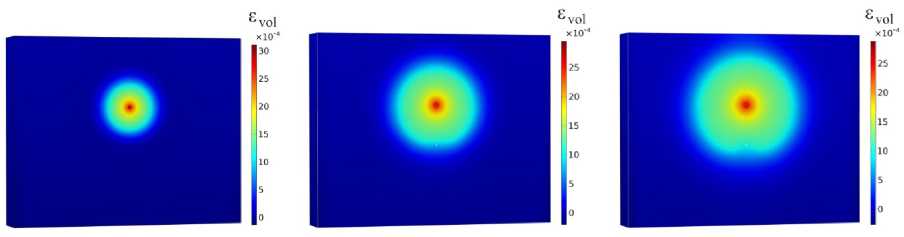
Рис. 11. Распределение величины объемной деформации по расчетной области, полученное при использовании модели пористости (19): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 11. Evolution of volumetric strain obtained with the use of porosity model (19) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

а                               б                               в

Рис. 12. Распределение температуры по расчетной области, полученное при использовании модели пористости (21): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 12. Evolution of temperature field obtained with the use of porosity model (21) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

а                               б                               в

Рис. 13. Распределение по расчетной области паронасыщенности совместно с наложенным полем скорости, полученное при использовании модели пористости (21): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 13. Evolution of steam saturation together with the velocity field obtained with the use of porosity model (21) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

а                                 б                                 в

Рис. 14. Распределение нефтенасыщенности по расчетной области, полученное при использовании модели пористости (21): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 14. Evolution of oil saturation obtained with the use of porosity model (21) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

б

а

в

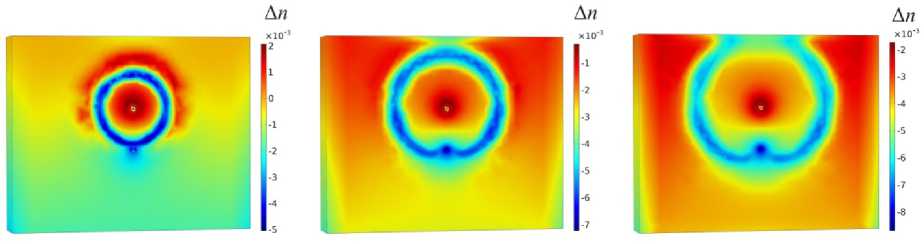
Рис. 15. Распределение изменения пористости по расчетной области, полученное при использовании модели пористости (21): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 15. Evolution of porosity change obtained with the use of porosity model (21) for (a) – 20th day; (b) – 60th day; (c) – 100th day o', Па                                □', Па                                  o', Па

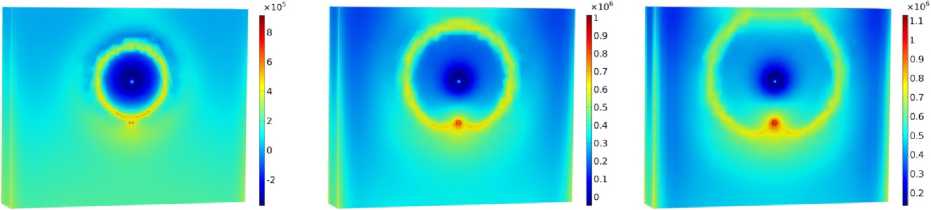
а                                 б                                 в

Рис. 16. Распределение эффективного напряжения по расчетной области, полученное при использовании модели пористости (21): а – 20-й день; б – 60-й день; в – 100-й день

Fig. 16. Evolution of effective stress obtained with the use of porosity model (21) for ( a ) – 20^th day; ( b ) – 60^th day; ( c ) – 100^th day

На рис. 17 приведено распределение параметра An = n100 - n0 (разность между значением пористости на 100-й день и начальным значением) вдоль горизонтальной прямой, расположенной на расстоянии одного метра от кровли пласта (рис. 17, а), и центральной вертикальной прямой, соединяющей кровлю пласта с нагнетательной скважиной (рис. 17, б). Область вблизи кровли пласта представляет наибольший интерес, поскольку считается, что начальный период формирования паровой камеры заканчивается по достижении ее границы. Полученные данные показывают качественно и количественно различные результаты. Модели (20), (22) предсказывают малое изменение пористости. Наибольшее отличие по сравнению с начальным значением дает модель (21), которая показывает, что в окрестности паровой камеры существует область, в которой изменение пористости принимает постоянное значение, максимальное по абсолютной величине. Возрастающие ветви на рис. 17, а соответствуют тем частям расчетной области, куда паровая камера еще не успела распространиться. Возрастающий участок на рис. 17, б вызван наличием вокруг паровой камеры области повышенного порового давления радиусом 3 м, которое стремится расширить поры. Похожий, но менее ярко выраженный характер имеют результаты, полученные при помощи формулы (22). Соотношения (17), (18) дают противоположную формулам (21), (22) картину. Их применение позволяет описывать увеличение пористости вследствие влияния порового давления. При этом на рис. 17, а наи- большее значение пористости соответствует отрезку, пересекающему паровую камеру, а на рис. 17, б максимум совпадает с границей скважины, где задано давление нагнетаемого пара. Таким образом, соотношения (17)–(22) дают принципиально разные, как качественно, так и количественно, результаты.

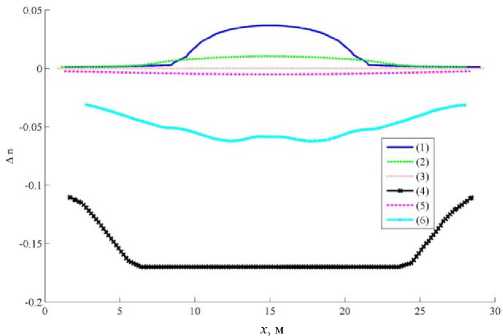
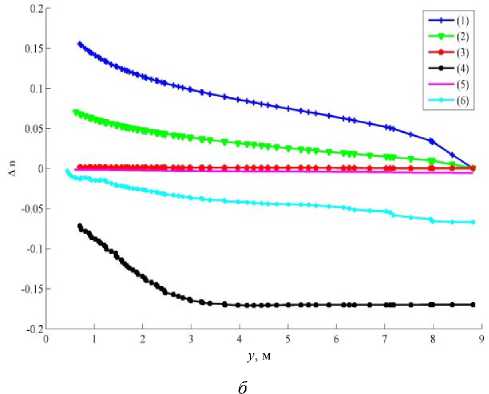
Рис. 17. Изменение пористости на 100-й день после начала ПГД, рассчитанное согласно различным моделям: 1 – формула (17); 2 – формула (18); 3 – формула (19); 4 – формула (20); 5 – формула (21); 6 – формула (22)); вдоль– горизонтальной линии, расположенной на расстоянии 1 м от кровли пласта ( а ); вдоль центральной вертикальной линии, соединяющей кровлю пласта с нагнетательной скважиной ( б )

Fig. 17. Change of porosity for 100^th day obtained by various models: 1 – formula (17); 2 – formula (18); 3 – formula (19); 4 – formula (20); 5 – formula (21); 6 – formula (22)) along the horizontal line located 1 m from the upper boundary of the reservoir ( а ); along central vertical line which connects the upper boundary of the reservoir with the injection well ( b )

Проведенное исследование моделей пористости позволяет заключить, что для корректного описания дебита нефти в произвольном пласте-коллекторе необходимы дополнительные лабораторные испытания, позволяющие определить преобладающий механизм изменения пористости (температурное расширение, поровое давление или сжатие пласта под действием нагнетания пара). Выбор формулы для расчета пористости будет зависеть от установленного механизма.

Заключение

В работе предложена связанная термогидромеханическая модель фильтрации многофазной жидкости в пористой среде для описания парогравитационного дренирования. Модель описывает процессы конвективного теплообмена, фазового перехода, теплового расширения грунта и влияние порового давления на напряженно-деформированное состояние продуктивного пласта. Для ее реализации был разработан алгоритм, основанный на решении системы уравнений относительно неизвестных величин давления, паро-, водо- и нефтенасыщенностей.

На основе разработанной модели проведено исследование особенностей различных соотношений для описания эволюции пористости. В результате было получено три характерных, качественно различных картины ее распределения по расчетной области. Модели первого типа основаны на установлении закономерностей между пористостью и поровым давлением. В результате их применения образуются две области, одна из которых расположена вблизи нагнетательной скважины (в ней пористость увеличивается), а другая – вблизи добывающей (пористость уменьшается). При связи пористости с объемной деформацией можно наблюдать увеличение пористости вследствие теплового расширения грунта. Для моделей третьего типа характерна зависимость от эффективных механических напряжений. В этом случае при паротепловом воздействии на продуктивный пласт образуется «кольцо» повышенного уплотнения грунта, которое соответствует фронту фазового перехода. Количественные расхождения между моделями могут достигать нескольких порядков. Результаты расчетов также показали, что применение различных моделей пористости приводит к изменению размеров паровой камеры, что влияет на оценку дебита нефти.

Таким образом, проведенное исследование моделей пористости позволяет заключить, что для корректного описания дебита нефти в произвольном пласте-коллекторе необходимы дополнительные лабораторные испытания, позволяющие определить преобладающий механизм изменения пористости (температурное расширение, поровое давление или сжатие пласта под действием нагнетаемого пара).

Работа выполнена при финансовой поддержке гранта Президента Российской Федерации для государственной поддержки молодых российских ученых МК-4174.2018.1 и программы президиума РАН 16 «Развитие физико-химической механики поверхностных явлений как фундаментальной основы для разработки современных конструкций и технологий».

Acknowledgment

The work was supported by the grant of the President of Russian Federation for support of young Russian scientists MK-4174.2018.1 and the Presidium of the Russian Academy of Sciences (program no. 16 “Development of Physicochemical Mechanics of Surface Phenomena as the Fundamental Basis for the Development of Modern Structures and Technologies).