Анализ моделей воспроизводства промысловых рыб с нелинейной интерпретацией данных наблюдений
Автор: Переварюха Андрей Юрьевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 1-1 т.18, 2016 года.
Бесплатный доступ
Рассматривается проблема методов подтверждения соответствия наблюдаемой динамики промысловых популяций рыб трем возможным режимам поведения траекторий дискретных динамических систем. Многие применявшиеся популяционные модели с качественными изменениями поведения оперируют с не интерпретируемыми с точки зрения экологии вида характеристиками, как знак третьей производной второй итерации от функции воспроизводства в момент потери устойчивости стационарной точки. На примерах показывается, что статистическая аппроксимация данных наблюдений приводит к зависимостям, исключающим наблюдаемое в реальности развитие популяционного процесса. Обсуждаются критерии, которыми можно пользоваться при анализе результатов вычислительного моделирования с точки зрения биологической адекватности. Предполагается, что скорость изменения численности в модели должна иметь интервал отрицательных значений, а кривая воспроизводства как минимум две нетривиальные стационарные точки. Учет действия экологического эффекта Олли в моделях будет способствовать лучшей сущностной интерпретации, разграничению возникающих в дискретных итерационных системах нелинейных эффектов и введет понятие о критически низкой численности промысловой популяции.
Динамика популяций, нелинейные и циклические режимы, интерпретация моделей
Короткий адрес: https://sciup.org/148204331
IDR: 148204331 | УДК: 629.075
Текст научной статьи Анализ моделей воспроизводства промысловых рыб с нелинейной интерпретацией данных наблюдений
как тождественные модели и их флуктуации априори считаются эквивалентными.
Иногда даже имея данные статистики об объекте моделирования нельзя ни подтвердить, ни опровергнуть адекватность модели, одна из причин в том, что разные функциональные итерации могут демонстрировать сходные режимы поведения. Во-вторых, данные полученные от наблюдения популяции в стационарном состоянии и при некотором переходном режиме могут совершенно по-разному интерпретироваться, хотя подчиняться одной и той же зависимости. В статье мы рассмотрим особенности восприятия данных наблюдений о промысловых популяциях, когда их способность к самовосстановлению предполагается в значительной мере обусловленной нелинейной зависимостью эффективности воспроизводства от численности нерестового запаса.
ДАННЫЕ И ДИНАМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Рассмотрим ситуацию, когда информация о популяционных процессах для конкретной экосистемы имеется и ставится задача разработки модели обладающей прогностическими возможностями. Естественно заметить, просто данных для построения модели недостаточно, необходимо биологическое обоснование для формализации исследуемого процесса. Существует множество классификаций моделей, но именно лежащее в основе математической модели теоретическое обоснование с точки зрения предметной области позволит классифицировать и сравнивать модели между собой, а главное принципиально их модернизировать. Результаты исследования модели аналогично обязаны получить обоснование в рамках биологической проблематики.
Если имеются данные и уже существует модель, разработанная на основе явных представлений о причинно-следственных связях в развитии процесса, то возникает задача настройки модели согласно имеющимся данным. Однако, данные были получены об объекте, находящемся в определенном состоянии и испытывающим внешнее, как говорят математики «управляющее» воздействие. Если объект не лабораторная популяция, и мы не можем произвольно управлять её состоянием, то хорошо бы точно знать тип состояния, в котором находился объект, о котором собрана статистика.
Обратимся к работам по исследованию процесса формирования пополнения популяций рыб. Основополагающие работы в этой области моделирования изначально отличались большей практической направленностью, так как они основывались на имеющихся данных по различным популяциям, которые приводятся в виде графиков. После появления известных моделей (ихтиологи называют их кривыми воспроизводства) Рикера, Кушинга или Бивертона-Холта формализующих компенсационную зависящую от плотности смертность молоди рыб нужно было разработать методы для настройки параметров кривых по данным. Можно сказать, что подобные двухпараметрические модели не так сложны, однако они могут включаться в состав объемных многокомпонетных моделей ихтиоценозов, как например В.В. Канторина для омуля оз. Байкал [3], Михайлова В.В., Решетникова Ю.С. для сига оз. Севан [4], и в качестве ведущих нелинейных членов определять их качественное поведение.
В разработке модели водного сообщества в [5] бифуркационным параметром для длиннопериодических колебаний оказался рост скорости пополнения зоопланктона, но не исключено что не единственно возможным.
Задаче подбора значений параметров посвящен один и разделов книги Рикера [6], где предложены возможные способы оценки. Для построения кривых воспроизводства предлагались довольно сложные преобразования исходных данных наблюдений. Исследователи склонны проявлять изобретательность, когда ставят цель подтвердить их теоретические предположения. Рикер логарифмировал предложенную им функцию f ( 5 ) = aS exp( - bS ) вычисления полонения R от запаса S следующим образом:
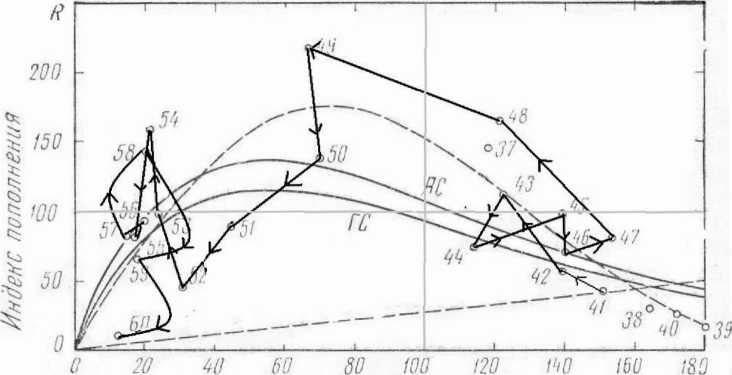
In R - In S = In a - bS и далее строил кривую с использованием регрессии InRIS на S для геометрической и арифметической средней, как показано на рис. 1 для норвежской трески, но ни одна из линий регрессии на этом графике не отвечает опытным данным. Однако, если прочертить траекторию, то станет видно, как популяция под воздействием какого-то важного фактора после 1948 г. переместилась из устойчивого стационарного состояния в неустойчивое равновесие. Эффективность воспроизводства после 1949 г. резко падала, потом столь же резко возросла, описав петлю, вышла к минимальному за время наблюдению значении. Далее промысловый запас по видимому деградировал (ряд данных заканчивается 1960 г.).
На графиках рис. 1 искалась именно куполообразная кривая, но вероятно реальная зависимость с такой динамикой выглядит сложнее. Мы можем предложить альтернативную модельную зависимость родительского запаса и восполнения для рассмотренной Рикером ситуации промысла трески с двумя экстремумами максимумами, один из которых образует пологий купол и содержит
Индекс величин родительского запаси
Рис. 1. Поиск зависимости Рикером по линиям регрессий с добавленной траекторией
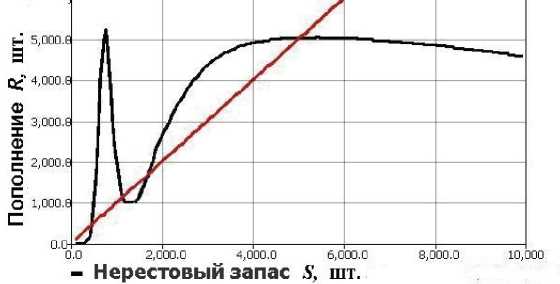
Рис. 2. Модельная зависимость с пиком и пологим куполом
притягивающую стационарную точку, а другой резкий пик между нетривиальными стационарными точками равновесия (рис. 2). Положение минимума может определяться дополнительными внешними факторами, вызывающими масштабирование кривой вдоль оси ординат и соответственно появится вероятность притяжения траектории к тривиальному равновесию точке 0,0.
Трудно предложить общую методику анализа статистики наблюдений за популяцией, рассматриваемой как естественная динамическая система, но находящейся за период наблюдений в различных режимах изменения состояния, например после селективного перелова. Обсуждение реальных наблюдений по теории формирования пополнения показывает, что проявление искомой зависимости гораздо в большей степени свойственно анадромным рыбам. Осетровые и крупные лососевые отличаются по продолжительности жизненного цикла, но сходны по экологическим условиям нерестовой миграции на ограниченные по площади пригодные пресноводные нерестилища.
Другой замечательный пример попытки построения кривой воспроизводства Рикера по детерминированным данным на рис. 3 интересен с точки зрения нелинейной хаотической динамики [7]. По оси абсцисс запас, по ординат пополнение и очень разумно оставлены даты соответствующие значениям на графике. Обратим внимание, что точки в плоскости запас×пополнение лежат точно по стрелкам траектории, проведенным нами от биссектрисы координатного угла геометрического места стационарных точек (диаграмма движения точек «лестница Ламерея»), так как это данные о численности тихоокеанской горбуши с двухлетним жизненным циклом. У некоторых лососёвых рыб существуют так называемые «четные» и «нечетные» стада, которые приходят на нерест соответственно в четные и нечетные годы, фактически размножающиеся отдельно разные популяции, взаимно конкурирующие. Численность четных и нечетных стад может значительно отличаться и в некоторых нерестовых реках одного из стад горбуши может не быть совсем. Для горбуши иногда отмечаются весьма резкие изменения численности производителей. Судя по траектории на таком графике мы предположим, что зависимость опять неунимодальная, но нет нетривиальной стационарной точки левее пика, ветвь кривой лежит ниже биссектрисы, и более того все возможные стационарные точки возле пика неустойчивы. Апериодическая динамика может реализовываться за счет интервального аттрактора, третьего типа по классификации предельных асимптотических множеств для итерационных систем Дж. Гукенхеймера.
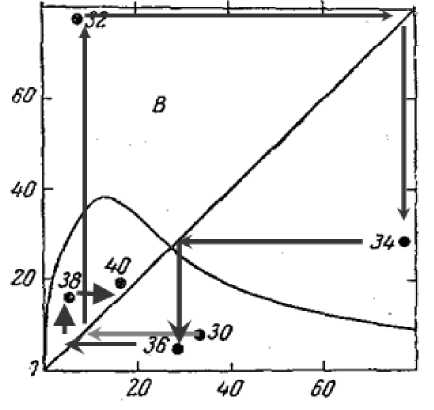
Рис. 3. Данные и попытка их аппроксимации кривой воспроизводства
Динамика системы начиная с точки 1930 г. по имеющимся данным в строгом смысле апериодическая. Однако, нарисованная аппроксимационная кривая обладает единственной стационарной точкой пересечения с биссектрисой, которая, судя по приведенному графику, должна быть устойчивой под действием итераций, так как наклон касательной к кривой в точке пересечения явно меньше π/4. Колебаний с большой амплитудой такая кривая предсказывать не может, так как точки должны были бы группироваться в некотором ограниченном радиусе от биссектрисы координатного угла или демонстрировать стягивание, т.к точка 34 отображается прямо на пересечение.
В работах Рикера ничего не сказано, что параметры моделей не равноценны по значимости при рассмотрении их влияния на структуру фазового портрета динамической системы. В предыдущей работе [8] мы отмечали бифуркационные изменения поведения модели Рикера, но в действительности эти свойства относятся к целому классу дискретных отображений, к которому относится и проведенная Рикером на рис 3. аппроксимационная кривая. К тому же типу отображений относится и модель Дж. Шепарда, как и совсем не имеющие отношение к популяционной динамике тригонометрическое отображение x n + 1 = X sin n xn . Модель Бивертона-Холта имеет совершенно другое качественное поведение : без циклов. Данные о четной популяции горбуши заставляют усомниться в том, что для нее существует зависимость пополнения и запаса с единственным максимумом, так динамика точек не характерна даже для случая образования хаотического аттрактора в результате накопления каскада удвоенных циклов.
ПРОТИВОРЕЧИВОСТЬ 2n-ЦИКЛОВ И ПЕРЕМЕЖАЕМОСТИ
Как известно в моделях Рикера и Шепарда существует возможность появления при бифуркациях циклов всех степеней 2, в результате бесконечного каскада таких удвоений поведение траектории хаотизируется. Но трактовка параметров, при которых увеличении которых происходят бифуркации удвоения периода, в этих двух моделях диаметрально противоположна. На рис. 4. цикл из четырех периодических точек модели Рикера, между двумя верхними и нижними точками ранее была одна точка, которая раздвоилась, но порядок обхода из верней ветви в нижнюю и обратно сохраняется при всех удвоениях.
Обнаружение универсального характера образования циклов было воспринято с позитивной стороны подтверждения предсказательных возможностей таких моделей для популяций с неперекрывающимися поколениями, начиная с работ Р. Мэя [9], и такое мнение продолжает доминировать среди математиков. Цикличность свойственна ряду природных популяций. Особенно выражены циклические изменения численности у грызунов субарктической зоны. Помимо длины циклы различаются взаимным расположением точек, и как мы видим у полевки Myodes rufocanus рис. 5, это монотонные перестановки с явным пиком в конце 4-летнего периода, и в конце сдвиг к 5-летнему.
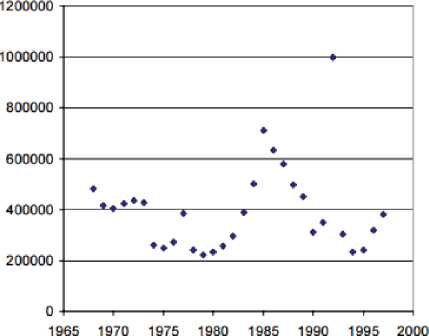
Согласно модельным циклам периода 2 n не будет периодов депрессии и промежутков высоких уровней. Для отдельных популяций лососевых свойственны длиннопериодические циклические колебания с постепенным приближением к наибольшим значениям (рис. 6). В
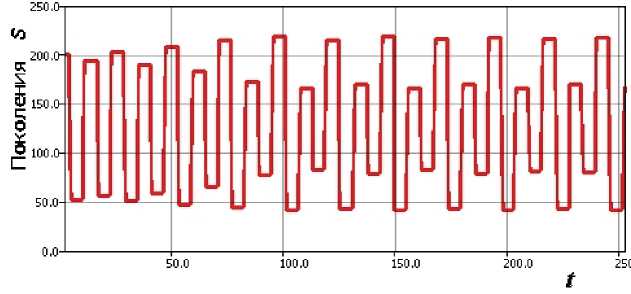
Рис. 4. Цикл периода 22 возникший в модели Рикера
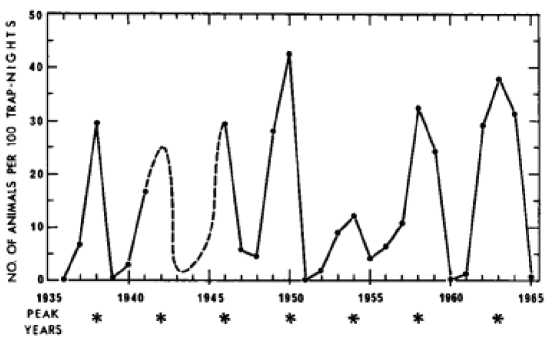
Рис. 5. Реальная 4-летняя цикличность популяции полевки из [10]
дискретных итерациях получить такую динамику проблематично, например нами предложен принудительный способ: вводить специальные триггерные функционалы редуцирующие «по ходу» число стационарных точек. Трудно предложить модель для пологого «соскальзывания» с пика как на рис. 6, эта ситуация сложнее резкого обрыва после вспышки численности насекомых. Можно вводить какой-либо циклически изменяющийся фактор внешнего воздействия, например для объяснения использовались 11-летние циклы солнечной активности. В таком определенном силами из внешнего мира случае зависимость пополнения и нерестового стада лучше описывать дробно-линейной гиперболической кривой, но что делать с дополнением, если мы очевидно наблюдаем на графиках данных наличие экстремумов?
Для динамических систем после образования хаотического аттрактора наблюдается возникновение периодических окон, в том числе нечетных периодов. Перед тем как перейти устойчивому циклу реализуется режим перемежаемости, когда длительное почти периодическое поведение прерывается апериодическими интервалами. Можно было бы говорить о популяционном истолковании подобного поведения траектории, однако амплитуда непериодических флуктуаций при перемежаемости наоборот уменьшается (стрелкой на рис. 7) по сравнению с амплитудой почти циклического движения.
Монотонные циклы, как следует из теоремы Шарковского, тоже могут возникать в рассмотренных моделях, но только когда значение управляющего репродуктивного параметра уже намного больше того, при котором появляется хаотическое движение.
ПОПУЛЯЦИОННАЯ ДИНАМИКА И КРИТЕРИИ СИНГЕРА
Будем рассматривать отображение класса гладкости С 2 отрезка прямой R 1 в себя задаваемой функцией f ( x ), которая будет интерпретироваться как связь между нерестовым стадом и образовавшимся пополнением у рыб неперекрываю-щимися поколениями. Пусть неподвижная точка отображения зависеть от нескольких параметров:
x * = x * ( a , b ), но f ' x ( x * ) = p ( a ),
t (years)
Рис. 6. Динамика нереста лосося (все виды) в Snake River, Канада
Для насекомых фитофагов встречается усложненная динамика, когда раз за разом периоды длительной депрессии вредителя сменяются переходом к флуктуациям с большой амплитудой и высокой средней за период численностью. Существующие гипотезы объясняет это воздействием распространения вирусных инфекций [11].
f '( x ) ^ 0 если x Ф c , f "( c ) Ф 0
и пусть для f ( x ; x Ф c ) всюду определен дифференциальный инвариант Шварца:
s = f"(x) _ 3 Г f» Y f f Xx) 2 ( f xx) J •
В случае функции Рикера имеем:
f'(x) = ae bx (1 - bx), f"(x) = abe bx (bx - 2), f"'(x)=ab2e-bx(3-bx) и в общем виде:
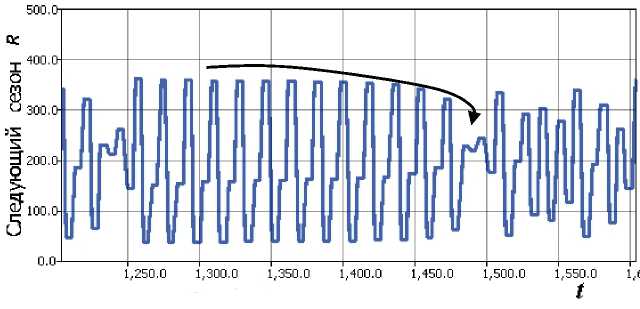
Рис. 7. Перемежаемость в модели рядом с возникающим циклом 3
f ( n ) ( x ) = a ( - 1) n b n 1 e bx ( bx - n ) .
Получим оценку знака шварциана, сохраняющегося для всех f ( f (...( x )...)) = f ” ( x ) :
— b x + 4 bx — 6
Sf = b ---------^— и очевидно S f < 0 для x е л .
f 2(1 — bx )2
Стационарная точка функции Рикера зависит от двух параметров: x = ln a I b , но критерий устойчивости однопараметрическая функция, и x * теряет устойчивость при:
f'(x*) = -1, где критерий устойчивости f -(x*) = a(1 -ln a) = 1 - in a.
e in a
При a = e 2, f '( x ) = - 1 наблюдается следующая ситуация для второй итерации f 2( x ) в теряющей устойчивость стационарной точке x :
df 2 ( x * ) = 1
dx d2f 2(x) _ df'(f (x))f'(x)
dx 2
d 2 f 2 ( x ') dx 2
dx
= f '( x * ) f "( x * )( f '( x * ) + 1)) = 0.
= f "( f ( x ))( f '( x )) 2 + f '( f ( x )) f "( x ),
и шварцициан S f 2( x *)
d3f 2 ( x *) dx 3
.
Так как известно S ^2< 0 , а следовательно df 2(x)/dx при a = е 2имеет в x * локальный максимум и таким образом происходит бифуркация, появляются устойчивые циклические точки, являющиеся стационарными точками для второй итерации. Очевидно, что отрицательный знак шварциана служит критерием для возможности реализации бесконечного каскада бифуркаций удвоения периода цикла, о важности которого для моделей математической биологии отмечалось автором ранее. Более того, это является следствием фундаментальной теоремы Д. Сингера [12], доказавшего, что отображение унимодальной функции с отрицательным дифференциальным инвариантом Шварца (критерии Сингера) S f может иметь не более одной устойчивой траектории и эта траектория является ю -предельным множеством для критической точки c : f '( c ) = 0 .
Следовательно, предложенная Рикером биологическая модель с математической точки зрения классифицируется как SU-отображение, для которого выполняются условия теоремы Д. Сингера. Модель Рикера отличается от объектов, исследовавшихся Фейгенбаумом и в других работах по универсальности (обычно квадратичного полинома) наличием точки перегиба f"(xs) = 0, xs = 21 b и точек, где обращаются в ноль старшие производные. lim f(x) ^ 0 озна-x ^^
чает, что хаотический аттрактор может увеличивать неограниченно, так как не возникнет такого явления как граничный кризис аттрактора.
Не относятся к данному классу отображений дискретно-непрерывная модель, предложенная нами в [8] для анализа порогового эффекта в воспроизводстве истощенного промыслом и малочисленного в настоящее время стада волжского осетра. Для незнакопостоянности инварианта S f достаточно получит зависимость с двумя точками с 1 , с 2 такими что f "( c 1 ) = f "( c 2 ) = 0. Нарушение критериев Сингера совсем не означает, что динамика итераций зависимости обязательно будет тривиальной.
Иногда более успешно применяются виды зависимостей казалось бы не соответствующие наблюдаемой форме кривой, так в [13] отмечается что данные по уловам сибирского осетра в верховьях Оби приводят к куполообразной форме кривой с плоской вершиной, но выбрана автором и используется модель Бивертона-Холта - дуга гиперболы. В интересной работе [14] о прогнозировании достаточно парадоксального увеличения эффективности воспроизводства камчатского кижуча лучшее соответствие показала альтернативная модель (хотя к сожалению для нелинейщиков она уступила в рейтинге авторов [14] авторегрессионной) теории формирования пополнения Шепарда:
f ( x ) =
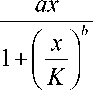
где а >1 интерпретируется аналогично модели Рикера, K так же, как и в известном дифференциальном уравнении П. Ферхюльста: лимитирующий фактор ограниченной емкости среды, степень воздействия которого определятся показателем b . Данная модель претендовала на универсальность в теории зависимости запаса и пополнения для рыб [15].
Рассмотрим модель Шепарда с точки зрения теории бифуркаций отображений на R 1 :
x * = Kba — 1, df (x) = (Kb + xb) aKb — ab (Kx)b dx (Kb + xb )2 , df (x *) a — ba + b
—- =--------> 0 при b < 1.
dx a
Теория универсальности нелинейных систем разработана только для однопараметрического случая [16]. Экспериментально установлено, что в ограниченном диапазоне значений параметра а, имеющих смысл, бифуркации удвоения периода возникают при изменении показателя степени b >>1 . При b <1 критических точек нет, при b =2
функция имеет критическую точку x=K . Вторая производная в критической точке:
d2 f (x )_ a dx2 = 4K , и функция имеет максимум при данных условиях. В случае модели Шепарда мы имеем сложную параметрическую зависимостью для аналитического анализа бифуркаций и так ихтиологическая практика ставит проблемы для математики.
Сущностная популяционная интерпретация нелинейных эффектов в моделях Рикера и Шепарда оказывается прямо противоположной. Рассмотрев изменение поведения модели Рикера, можно сформулировать гипотезу: увеличение репродуктивного потенциала популяции (переход к r -стратегии вида) приводит к флуктуациям численности до апериодического характера. В реальности колебания свойственны не только и видам r -стратегам, но K -стратегам, так в национальном парке Крюгера ЮАР ведут борьбу с флуктуациями слонов. В модели Шепарда появление циклов периода 2 n происходит при увеличении действия лимитирующих факторов среды. Можно предположить: 1) одна из двух моделей принципиально неадекватна 2) каскад бифуркаций и ряд нелинейных эффектов (окона периодичности, перемежаемость, внутренний кризис хаотического аттрактора) для SU- отображений не имеет сущностной популяционной интерпретации.
Следствие 1. Функциональная зависимость, соответствующая условиям теоремы Сингера, будет выходить за пределы применимости в популяционной динамике при непредсказуемых интервалах значений модельных параметров.
Следствие 2: Модель функциональной зависимости «запас-пополнение» не должна сохранять знакопостоянный шварциан, т.е. каскад бифуркаций должен останавливаться.
Параметр a характеризует репродуктивный потенциал, но это для популяций стабильная величина, плодовитость биологических видов имеет эволюционно сложившееся значение, и непонятен вопрос: почему она должна резко увеличиваться? Случай увеличения числа генераций за сезон нельзя описывать простым изменением a .
Для случая с осетром Каспия нам было важно рассмотреть в модели воспроизводства ситуацию приближения к минимальной для выживаемости численности нерестового стада, но как оказалось, подобные зависимости будут иметь и другие отличия динамики. Можно выдвинуть критерии, при соблюдении которых модель сохранит адекватность, если рассмотреть известный в популяционной биологии эффект Олли применительно к удельной скорости роста и дать интерпретацию величине y = df ( x ) / dx.
Предложим следующие условия, накладываемые на производную: не должна быть унимодальной функцией, а именно:
-
а ) y ( x ) должна достигать максимума на промежутке (0,c);
-
б ) иметь минимум на промежутке (c,d), где y ( c ) = 0, y ( d ) < 0;
-
в ) lim y ( x ) = 0.
x ^^
Таким образом, учет проявления на графике действия эффекта Олли, выражающегося в непропорциональном падении эффективности воспроизводства относительно сокращающегося нерестового запаса, практически расширит рамки возможности интерпретации результатов вычислительного моделирования.
Остается краеугольный вопрос, если применимы модели, для которых не наблюдается каскада бифуркаций, то как модельно интерпретировать данные о популяциях, явно характеризующихся циклической и апериодической динамикой? Ответ состоит в отказе от условия единственности экстремума функции f ( x ). В итерациях неунимодальных функций (имеющих более одного максимума воспроизводства) возможно возникновение интервальных «подковообразных аттракторов» с апериодической динамикой ограниченной амплитуды. Дополнительно в отображениях с несколькими экстремумами возможно явление мультистабильности и практически стохастического выбора одного из альтернативных устойчивых состояний.
ЗАКЛЮЧЕНИЕ
Принципы экологии часто не согласуются со свойствами математического аппарата. Чем больше видов в экосистеме, тем она стабильнее и продолжительное время сохраняет свое состояние. В тропическом лесу не происходит вспышек численности, не один вид не может стать доминирующим из-за напряженности конкуренции за ресурсы. При увеличении размерности фазового пространства усложняется многообразие режимов поведения траектории динамических систем. Выводы, сделанные на основе численного исследования многих абстрактных моделей, диктуются фундаментальными свойствами математических объектов. В моделях систем, описываемых тремя дифференциальными уравнениями возможно возникновение странных хаотических аттракторов двух типов: бабочки Лоренца или волчка Рёслера. В системах из четырёх уравнений может наблюдаться уже появления так называемого «гиперхаоса», когда изначально близкие траектории могут экспоненциально разбегаться сразу в двух направлениях. Включение в уравнение запаздывания аналогично усложняет вид флуктуаций. В дискретной динамике запаздывание можно рассмотреть, если перейти к непрерывно-событийному описанию репродуктивного процесса и учесть запаздывания не для всей популяции как в варианте модели из [17], а только для одной из стадий развития анадромных рыб.
Многообразие режимов поведения нелинейной модели трудно втиснуть в ограниченные рамки сущностной интерпретации, если модель не абстрактная, но строится исходя из реального состояния промысловой популяции. На этапе разработки модели исследователь не может предполагать всех странностей её динамики. В то же время анализ экспериментальных данных без учета основ нелинейной динамики приводит противоречивым результатам, как установлено на примерах из работ в области модельного исследования динамки популяций рыб. В работе показано, как выработка определенных критериев, накладываемых на модели конкретной предметной области, может упростить проблему объяснения полученных результатов. Интересным способом улучшения практических результатов моделирования видится сценарный подход, подразумевающий сравнительное сопоставление сразу серии управляемых вычислительных экспериментов по отношению к изменяемому внешнему параметру.
Список литературы Анализ моделей воспроизводства промысловых рыб с нелинейной интерпретацией данных наблюдений
- Гаузе Г.Ф. О законах накопления биомассы в смешанной культуре двух видов дрожжей//Известия Академии наук СССР. 1933. № 10. 1465-1467
- Utida S. Cyclic Fluctuations of Population Density Intrinsic to the Host-Parasite System//Ecology. 1957. Vol. 38. P. 442-449.
- Конторин В.В. Математическое моделирование популяции байкальского омуля. М.: 1980. 208 с.
- Михайлов В.В., Решетников Ю.С., Щеголев А.Г. Имитационная модель рыбной части сообщества озера Севан//Проблемы автоматизации научных и производственных процессов. Л.: Наука, 1985. С. 56-61.
- Бобырев А.Е., Бурменский В.А., Криксунов Е.А., Медвинский А.Б., Нуриева Н.И., Русаков А.В. Долгопериодные эндогенные колебания численности популяций рыб. Математическое моделирование//Биофизика. 2013. Т. 58. № 2. С. 334-348.
- Рикер У.Е. Методы оценки и интерпретация биологических показателей популяций рыб. -М.: Пищевая промышленность, 1979.
- Ricker W.E. Two mechanisms that make it impossible to maintain peak period yields from stocks of Pacific salmon and other fishes//Journal of the Fisheries Research Board of Canada. 1973. Vol. 30. P. 1275-1286.
- Переварюха А.Ю. Моделирование порогового эффекта в эффективности воспроизводства волжской популяции осетра//Известия Самарского научного центра РАН. 2014. Т. 16. № 5-1. С. 548-553.
- May R.M. Qualitative Stability in Model Ecosystems//Ecology. 1973. Vol. 54. P. 638-641.
- Krebs C.J., Myers J.H. Population Cycles in Small Mammals//Advances in Ecological Research. 1974. Vol. 8. P. 267-399.
- Anderson R., May R.M. Infectious Diseases and Population Cycles of Forest Insects//Science. 1980. Vol. 210. № 4470. P. 658-661.
- Singer D. Stable orbits and bifurcations of the maps on the interval//SIAM journal of applied math. 1978. V. 35. P. 260-268.
- Журавлев В.Б. К методике изучения численности популяций редких и исчезающих видов рыб//Вестник Новосибирского государственного аграрного университета. 2012. Т. 2. № 23-2. С. 20-27.
- Фельдман М.Г., Шевляков Е.А., Зорбиди Ж.Х. Прогнозирование подходов лососевых (на примере кижуча западной Камчатки) с использованием моделей экстраполяции временных рядов и моделей «запас-пополнение»//Исследования водных биологических ресурсов Камчатки и северо-западной части Тихого океана. 2014. № 34. С. 87-106.
- Sheperd J.G. A versatile new stock-recruitment relationship for fisheries, and the construction of sustainable yield curves//J. Cons. Intern. Explor. Mer. 1982. V. 40. P. 67-75.
- Collet P., Eckmann J., Lansford O.E. Universal properties of maps of an interval//Gomm. Math. Phys., 1980, Vol.76, №3, p. 211-254.
- Михлин Л.С. Об устойчивости одной нелинейной модели с запаздыванием//Процессы управления и устойчивость. 2015. Т. 2. № 1. С. 65-70.


