Анализ модели движения запасов газа по категориям

Деятельность любой отрасли горнодобывающей промышленности характеризуется не только непрерывным расходованием запасов полезного ископаемого, но и его пополнением за счёт разведки. В зависимости от степени разведанности и изученности запасы газа подразделяются на различные по достоверности категории и группы. В соответствии с классификацией запасов горючих газов [1] геологические запасы природных газов и содержащихся в них сопутствующих компонентов, имеющих промышленное значение, по степени изученности подразделяются на разведанные категории А, В и Ci и предварительно оцененные - категория C2. Ресурсы газа по степени их обоснованности подразделяются на перспективные - категория C3 и прогнозные - категории Di и D2.

Таким образом, каждая категория характеризуется своим уровнем знаний о запасах (ресурсах) природного газа [2]. Знания о запасах (ресурсах) основываются на перечне работ, проведенных на изучаемых объектах, и информации, полученной из предыдущих категорий.

По мере исследования запасов (ресурсов) газа и перемещения его носителя из менее изученной категории в более изученную изменяется представление об объекте и его характеристиках. Также подвергаются изменению методы и способы определения тех или иных характеристик объекта, уточняется их количественная оценка. С учётом этих особенностей рассматривается математическая модель движения запасов природного газа по категориям.

Здесь и далее ресурсы газа мы будем называть запасами.

1.    Модель движения запасов природного газа по категориям

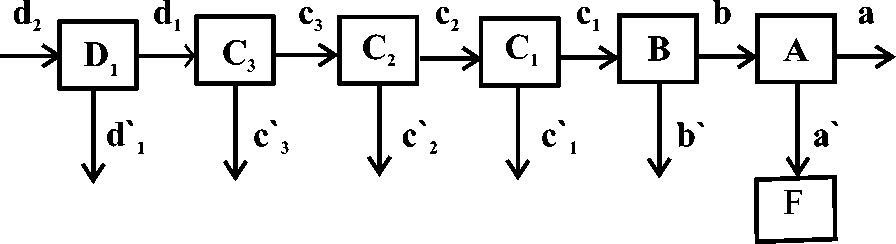
Рис. 1. Схема, движения запасов газа, по категориям

Перейдем к описанию математической модели единичного объекта, газодобычи, которым может быть отдельная залежь, месторождение или перспективная структура. Модель разработана, как составная часть системы планирования добычи газа. [3, 4] и предназначена, для составления с её помощью вариантов долгосрочных планов добычи газа, по региону, в котором расположена, группа, подобных объектов. В отличие от других известных авторам моделей газодобычи данная модель включает дополнительно разведку на. менее изученных объектах, что позволяет пополнять истощаемые в процессе разработки запасы газа. Модель позволяет скоординировать процесс движения запасов по категориям, учитывая различную степень их изученности.

Разведка в рассматриваемой модели осуществляется на запасах Д^СДСфСз и Di в соответствии с различной степенью их изученности. В процессе разведки меняются и уточняются наши представления о запасах газа, что приводит к переводу запасов из менее разведанных категорий в более разведанные и подготавливают основу для последующей добычи газа. Движение запасов природного газа, по категориям представлено на. рис. 1.

Здесь: А,в,с1,с2,сз и Di - объёмы запасов соответствующих категорий;

Ғ - объёмы запасов газа категории А, оставшихся не извлечёнными по технологическим или экономическим причинам; а - добыча природного газа;

а' - потеря запасов категории А, вследствие их неполного извлечения;

• b, ci, С2, сз, di и d2 - потоки запасов газа из соответствующих менее разведанных категорий в более разведанные;

• b', ci, c2, с3 и d’i - изменения запасов соответствующих категорий по причине неподтвер-ждения первоначальных данных при более детальной разведке.

В дифференциальной форме движение запасов газа во времени можно представить

следующими уравнениями:

А — b — а — а ,                                    (1) В = ci — b — b',                                      (2) С 1 = с2 — С1 — Д,                                   (3) С2 = с3 — с2 — с2,                                     А.) С3 = di — с3 — с3,                                        (б) D 1 = d2 — di — d^,                                       (6) Ғ = а'.                                             (7)

Введём понятие текущего коэффициента извлечения запасов У_а и понятие текущих коэффициентов подтверждаемости запасов У ь , У _с і , У_е2, У_ез и у ^ і соответствующих категорий

следующим образом:

а У а =    . ,; а + а b Уь = b + b' ; сі 7ci = сі + di ; с2 7C2 = с2 +   ' с3 7е3 = сз + сз • d1 7d1 = di + di ■

Уравнения (1) - (7) можно переписать в следующем виде:

А = b — -,                                   (8) У а b в = с і — -,                                    (9) У ь с i = с2 — ^^,                                  (10) У с і Сб 2 = с3---,                                          (11) Уе2 Сб з = di --,                                             (12) Уе3 і) i = d2 — ^^,                                   (13) Уш І^ = 1^^^ а.                                 (14) У а

В расчётах вариантов долгосрочных планов добычи газа по Северо-Тюменской газоносной провинции коэффициент т)_а принимали равным 0.85. При этом предполагалось, что оставшиеся 15% запасов газа находятся при низком давлении и могут быть в дальнейшем частично или полностью использованы под местные нужды. Подтверждаемость запасов зависит от категории, к которой они относятся. Это объясняется тем, что при переводе запасов из менее разведанных категорий в более разведанные мы получаем дополнительную информацию. С ее помощью уточняются многие характеристики, в том числе и объёмы запасов природного газа. В то же время подтверждаемость запасов одной и той же категории колеблется в некоторых пределах. Например, в зависимости от района для категории С2 подтверждаемость запасов колеблется от 0.3 до 1.0, а для категории Di подтверждаемость колеблется от 0.1 до 0.6-0.7.

Рассмотрим стационарный режим, когда

•              ■              ■                 ■                 ■■

А — В — Ci = С-2 = С-3 = Di в уравнениях (8) - (13) и, учитывая, что уа < 1, т)Ь < 1, yci < 1, ус2 < 1, т)с3 < 1, T)di< 1, получим следующее неравенство: d2 > d1 > с3 > с2 > с1 > b >а.

Как видно из последнего неравенства, в стационарном режиме потоки запасов природного газа из менее разведанной категории должны быть не меньше потоков из более разведанной категории.

• 2.    Кратность запасов

При планировании прироста запасов в газодобывающем районе с учётом различных категорий запасов особую роль играет коэффициент кратности запасов. Коэффициент кратности запасов подсчитывается для разведанных запасов природного газа и представляет собой частное от деления текущих разведанных запасов на годовую добычу газа w — А + в + с а

.

Таким образом, коэффициент кратности показывает, на сколько лет обеспечивают разведанные запасы добычу природного газа, если добыча его сохраняется на том же уровне, что и в настоящее время. Данную формулу для расчёта кратности запасов можно использовать в период растущей и постоянной добычи. При расчёте коэффициента кратности в период падающей добычи по формуле (15) мы наблюдаем, на первый взгляд, парадоксальную ситуацию. Добыча падает, а обеспеченность запасами растёт, что создаёт видимость благополучия. Это легко объясняется тем, что темп падения добычи больше темпа уменьшения разведанных запасов.

Вернёмся к схеме, показанной на рис. 1, и ограничимся рассмотрением только категорий разведанных запасов А,В и Ci. Для простоты изложения положим ту^, = у_с1 — 1. Тогда уравнения (8) - (10) перепишутся в следующем виде:

а А — ь — —,

У а

В — c_i — b,

Ci — С2 — Ci.

Сложим эти уравнения, получим

А + В + С i — С2 — -.                          (16)

У а

Введём новую функцию Ф^) такую, что ФД) — C2(t) и Ф(—от) — 0. Функция ФД) определяет суммарные запасы природного газа, разведанные ко времени t, т.е.

Ф(t) = С1 (t) + В (t) + A(t) + J a(t) dt + J a'(t) dt.

Производная Ф(t) - характеристика, определяющая эффективность поисковоразведочных работ. Как было установлено мировым опытом разведки, эффективность этих работ растёт в начальный период времени до достижения примерно 25-30% реализации начальных потенциальных ресурсов газа, а затем падает. Это объясняется тем, что в начальный период освоения территорий в разведку вовлекаются наиболее крупные залежи, а на завершающей стадии - мелкие, с более сложным геологическим строением. Такая закономерность наиболее ярко проявляется в Северо-Тюменской газоносной провинции.

Исходя из вышесказанного, можно предположить, что Ф(t) - возрастающая непрерывно дифференцируемая выпукло-вогнутая функция и Ф(то) = 0. Кроме того, если Ф(і) = 0 для некоторого момента t, тогда Ci (t) = 0; B(t) = 0; A(t) = 0; a(t) = 0; a‘(t) = 0 для t E (-^.t). Следует отметить, что такие особенности характерны для многих функций, в том числе и для производственных функций [5].

Обозначим разведанные запасы через R, т.е. R = А+В +С1, тогда формула определения кратности запасов (15) и уравнение (16) представляются в виде

W = -

a

;

R = (W a) = Ф - —.                           (17)

d a

Предполагаем, что коэффициент извлекаемости запасов d_a равен константе.

Рассмотрим несколько конкретных примеров. Будем считать, что процесс разработки запасов газа рассматривается при t > 0.

Пример 1. Пусть величина разведанных запасов остаётся постоянной, т.е. R = 0. Тогда из (17) вытекает

Wa = const и                                                            ^

Ф(t) = Ф(0) +-- I a(t) dt.

d a 0о

Исходя из предположения, что добыча в начальный период эксплуатации запасов растёт, затем стабилизируется и в конечный период эксплуатации падает, коэффициент кратности ведёт себя следующим образом. В начальный период он падает, затем постоянен и в конце эксплуатации растёт. Аналогичное поведение коэффициента кратности в конце эксплуатации мы наблюдали в случае, описанном в начале параграфа, но в отличие от него увеличение кратности здесь связано с пополнением запасов за счёт запасов категории С2.

В данном случае разведанные запасы пополняются таким образом, чтобы компенсировать потери, связанные с добычей природного газа, а также с неполным их извлечением.

Пример 2. Предположим, что добыча постоянна и Ф(0) = 0. Если Ф(0) = 0, то величина начальных разведанных запасов равна нулю. Из определения коэффициента кратности вытекает W (0) = 0. Уравнение (17) перепишется в следующем виде:

a aW = Ф.

d a

Отсюда следует

W(t) = 1Ф(t) - —. ad

Для того чтобы коэффициент кратности был положительным, необходимо на эффективность поисково-разведочных работ в начальный момент наложить ограничение

Ф(0) > -,(18)

da т.е. в начальный момент времени разведанные запасы должны пополняться с большим темпом, чем темп их расходования.

Так как Ф( от ) = 0, то существует момент времени t* >  0 такой, что W ( t* ) = 0. Иными словами, в момент времени t* расходуется весь разведанный запас. Таким образом, поведение коэффициента кратности корректно рассматривать только на временном отрезке [0 ,t*]. На этом отрезке времени коэффициент кратности положителен и сначала он растёт, а затем падает.

Пример 3. Предположим, что коэффициент кратности константа пФ(0) = 0. Из определения коэффициента кратности вытекает, что а(0) = 0. Перепишем уравнение (17) в виде а Ф a +     =

+ T)aWW

Проинтегрировав его, получим

1                t       Г4 - . А a(t) = wexp(—w)Z Фтнф(w)”■

Добыча природного газа для всех t >  0 положительна. Покажем, что для любой малой величины 5 > 0 предел lim₄^^ a(t) <  6т)_а. Решим у равнение Ф(t) = 6. Среди всех решений найдем максимальное решение и обозначим его через т. Преобразуем правую часть формулы (19). В результате получаем

1               t Г                А              1               t      Г⁴ • .          .А

^{a ( t )} = W ^exp( -^ )Уо ^exp^ ^{)dA +} w ^exp( -^ ⁾ Ут ^exp^ ^)d6<

< фехр( - ^t—-^ ^)ф (т) ⁺-¹ exp(--( )l ^ф(6⁾ехр⁽ Д )<№ <

W    ^aW      W    ^aW JT       ^aW

1 t — т                      t — т

< w ^{exp( —} ^w ^{)Ф( т )+ 6p}" ^{[1 — exp( —} ^w ^)]-                 ¹²¹¹¹

В неравенстве (20) перейдем к пределу lim₄^^ a(t) <  6^_а. Значит, добыча природного газа стремится на бесконечности к нулю.

Пример 4. Предположим, что добыча газа падает по линейному закону a ( t ) = a⁰ — at и Ф (0) = 0. Из предположения Ф(0) = 0 вытекает, что W (0) = 0. В этом случае решение уравнения (17) перепишется в следующем виде:

w ( t ) = ^{ф( t )}

a⁰ — at

-

a°t — 522

% ( а⁰ — at ) .

Для того чтобы коэффициент кратности был положительным, необходимо на эффективность поисково-разведочных работ в начальный момент наложить ограничение (18), т.е. в начальный момент времени разведанные запасы должны пополняться с большим темпом, чем темп их расходования.

Из (21) найдём все положительные значения t, при которых W (t) = 0. Среди всех положительных решений, удовлетворяющих W(t) = 0, найдём минимальное t >  0. Если t Е (0, ^ ), то коэффициент кратности положителен на интервале (0, t). В противном случае коэффициент кратности положителен на интервале (0, ^0).

Коэффициент кратности, определённый на полуинтервале [0, ^), стремится при t ^ ^° к бесконечности, а коэффициент кратности, определённый на отрезке [0, £] в момент времени t . обращается в нуль. К моменту t расходуются все накопленные за, время t разведанные запасы.

Пример 5. Рассматривается модель месторождения с взаимовлияющими скважинами, на основе которой были поставлены и решены многие интересные оптимизационные задачи [6-9]. Добыча газа на месторождении при постоянном темпе бурения скважин меняется по закону q0O a(t = q ntexp(-^ф^t ),

Ф(0) = / a(t) dt = [ q°nt exp(—x^^t²) dt,                  (22)

J о             Jo              ^2ф(и)

где q0 - начальный дебит скважины;

n - постоянный темп разбуривания месторождения.

Поскольку бурение скважин начинается в начале разработки месторождения, то количество скважин на месторождении в момент времени t определяется в соответствии с формулой N (t) = nt.

Следует отметить, что в этом примере начинают разбуриваться и покрываться равномерной сеткой скважин только запасы, разведанные к моменту t = 0. По величине эти запасы равны Ф(0), что отражается в описании формулы (22). Запасы, поступившие позже, резервируются и в рассматриваемом примере не разрабатываются. Однако они участвуют в подсчете коэффициента кратности запасов газа.

Рассмотрим в динамике поведение добычи газа. Добыча газа сначала равна нулю. Далее она возрастает и достигает своего максимального значения. Затем добыча падает и в пределе стремится к нулевому значению.

Проинтегрируем уравнение (17) с коэффициентом da., равным единице. В результате получаем exp( ч0™ t2)           rt                 о

W(t) =    Xо  [Ф(t) -   q°ntexp(-Xo)t2) < q nt           Jo            2ф(0)

Коэффициент кратности положителен. В нуле и на бесконечности он принимает бесконечное значение. Это связано с нулевой добычей природного газа в нуле и на бесконечности.

Пример 6. Предположим, что добыча газа падает по экспоненциальному закону a(t) = a⁰ exp(—at) и Ф(0) = 0. Из предположения Ф(0) = 0 вытекает, что W (0) = 0. В этом случае решение уравнения (17) перепишется в следующем виде:

W (t)a(t) = Ф(t)--[ a(t) dt.

da 0o или ф(t)      , .       1                            ф(t)       1 .       , .1

W(t) = —^exp(at)--[exp(at) — 1] = (—---) exp(at) +.

a0           «da                 a0    «da

Для положительности коэффициента кратности необходимо в начальный момент наложить ограничение (18).

Далее, если в некоторый момент t* выполнено неравенство Ф(t*) > Ду-. то, учитывая свойства функции Ф(t), приходим к выводу, что коэффициент кратности положителен для всех t > t*. В противном случае может существовать t такое, что W(t) = 0. т.е. к моменту t израсходуются все разведанные запасы.

3.    Заключение

Подведём краткие итоги изложенной в статье работы. В соответствии с классификацией запасов газа рассматривается динамическая модель движения запасов газа от менее изученных категорий запасов к более изученным категориям. Движение запасов газа завершается на наиболее изученной категории частичным или полным извлечением их из недр.

Между соседними категориями устанавливается связв, описываемая с помощвю дифференциальных уравнений. Исследованию подвергается стационарный режим, при котором в каждой категории величина запасов не меняется со временем. Делаются соответствующие выводы.

Далее вводится математическое определение кратности запасов и эффективности поисково-разведочных работ. Для запасов категорий А+В+С1 исследуются шесть режимов при различных предположениях о поведении добычи, кратности запасов и эффективности поисково-разведочных работ.

Построенную в работе динамическую модель можно использовать в качестве инструмента при планировании поисково-разведочных работ. Кроме того, модель может являться основой для дальнейших исследований и получения качественных и количественных результатов. Модель может быть детализирована. В неё могут быть включены элементы теории вероятности и математической статистики, что позволит в дальнейшем использовать модель в качестве инструмента при решении различных задач, в том числе при решении вопросов об экономической целесообразности разработки залежей и проведения поисково-разведочных работ.