Анализ начальной стадии усталостного износа гетероструктурных материалов в условиях контактных циклических нагрузок

УДК 620.22+620.178.3                                     

1, 2, 3, 4, 5 Don State Technical University, Rostov-on-Don, Russian Federation

Введение. Моделирование специфических непрогнозируемых явлений весьма актуально с точки зрения предотвращения их нежелательных последствий. Например, в аэронавтике, теплоэнергетике, газотурбинном производстве и сельском хозяйстве остается нерешаемой проблема каплеударной эрозии. Вопрос обсуждается на мировом уровне [1–4]. Первые успехи в моделировании этого явления касались единичных капельных соударений [5–10]. В некоторых работах [11–13] предприняты попытки количественно оценить способность материалов и покрытий сопротивляться действию динамических циклических нагрузок. В частности, удалось создать расчетно-аналитическую модель, апробированную в условиях жидкокапельного ударного воздействия [14–18]. Многие авторы [19–21] не дифференцируют поведение материала или покрытия на стадиях зарождения и развития разрушения. Зарождение весьма проблематично идентифицируется в эксперименте. В названной выше модели оно оценивалось с помощью эмпирических коэффициентов, не имевших универсального теоретического обосновании, и это явный недостаток решения. Цель настоящей работы — более глубокое теоретическое рассмотрение стадии зарождения дефектов в покрытии, приводящих к его износу и разрушению, а также создание на этой основе расчетного аппарата для определения момента зарождения трещин или пор в различных материалах и покрытиях в условиях циклического нагружения.

Материалы и методы. Трудности оценки стадии зарождения разрушения и износа при циклических воздействиях (например, при высокоскоростных жидкокапельных соударениях, провоцирующих каплеударную эрозию металлических изделий) связаны не только с инструментальным определением зародышей трещин или пор. На этой стадии наличие структурных элементов в материале не позволяет представить процесс непрерывным континуумом и использовать для расчетов линейную механику разрушения (например, усталостную теорию Пэриса — Эрдогана). Поэтому в механике разрушения начальная стадия зарождения усталостных дефектов выделяется в особый этап. Он называется «микроструктурная механика разрушения» и протекает вплоть до достижения дефектом размера l k = (4…10) ⋅ d , где d — размер структурного элемента материала [22]. Аналитическая оценка стадии зарождения усталостных дефектов требует, прежде всего, металлофизического подхода. Задача заключается в нахождении расчетного выражения для числа циклических нагружений N 3 , необходимых для формирования в материале усталостного дефекта критического размера. В качестве эмпирической базы расчетной модели можно использовать также экспериментальные данные стендовых испытаний на каплеударную эрозию, где роль N 3 выполняет количество капельных соударений.

В общем случае уравнение для числа динамических циклических нагружений N 3 должно включать три составляющие: механическую, кинетическую и структурную.

Металлофизическая концепция механической составляющей связана с числом (плотностью) подвижных дислокаций ρ m , возникающих при единичном ударном нагружении (соударении). В процессе многократных соударений количество подвижных дислокаций увеличивается, они перемещаются в металлической матрице по плоскостям скольжения под действием касательных напряжений σ s до тех пор, пока не сформируют на ближайших непреодолимых барьерах плоские скопления с критической плотностью ρ kr . Превышение ρ kr ведет к самопроизвольному разрыву межатомных связей в металле и образованию зародыша трещины. Значения ρ kr для различных материалов и покрытий известны [23]. Механическая составляющая числа соударений выражается в форме зависимости N ₃ = f ( ρ _kr / ρ _m ).

Машиностроение и машиноведение

Кинетическая составляющая числа соударений N 3 учитывает зависимость энергии дислокации от ее скорости V d . Из теории дислокаций известно, что по мере возрастания скорости дислокации ее энергия увеличивается в соответствии с выражением Эйнштейна для тел, движущихся со скоростями, близкими к скорости света. Только пределом для скорости дислокации является скорость звука в кристалле С 0 , при которой энергия дислокации становится бесконечной. Поэтому с учетом специфики каплеударного воздействия кинетическая составляющая числа соударений выразится как N 3 = f ( V d / С 0 ).

Структурная составляющая числа соударений N3 имеет два аспекта. Первый заключается в том, что движение дислокаций при ударе ограничено размерами структурного элемента матрицы D, в пределах которого возможен свободный пробег дислокаций. В общем случае в качестве такого элемента рассматривается размер зерна, а для тонких покрытий — его толщина. Второй аспект учитывает, что в пределах зерна или покрытия могут существовать препятствия для движения дислокаций: частицы вторичных фаз, малоугловые границы, закрепленные атмосферами неподвижные дислокации, дефекты упаковки, сопротивление решетки (напряжение Пайерлса). Как отмечено выше, оба эти аспекта отражены в структурной составляющей числа соударений, и она представляет собой функцию двух переменных N3 = f (D, AG), где AG — свободная энергия Гиббса для активации процесса преодоления препятствий, находящихся в пределах структурного элемента D. Механизм преодоления зависит от природы препятствия, что и определяет значение AG для каждого конкретного случая структуры материала (их классификация приведена в [23]).

Из сказанного следует, что все составляющие искомого числа соударений N 3 влияют на процесс формирования усталостного дефекта одновременно — при каждом соударении. Этот факт определяет коммутативный характер взаимодействия механической, кинетической и структурной составляющих. Тогда в наиболее общем виде N 3 определяется выражением

I г л2 -AG

N 3 ^ 1 -I V U . D . e kT , (1) Р m I C 0 J ¹ 0

где k — постоянная Больцмана; Т — термодинамическая температура, К; l 0 — путь, пройденный подвижными дислокациями за один цикл нагружения (соударение).

Выражение (1) получено на основе теории дислокаций и представляет собой теоретическую концепцию. Для использования (1) при оценке износостойкости материалов и покрытий в условиях циклических жидкокапельных соударений необходимо раскрыть входящие в него величины (такие как р m , Vd, l ₀, A G ) через измеряемые параметры соударения (например, скорость соударения V 0 и размер капли R 0 ). Авторы уже выполнили соответствующую детализацию модели (1) и готовят материал к публикации.

Результаты исследования. Расчетная модель апробирована для сплавов на основе железа различного состава и структуры. Такой выбор обусловлен, прежде всего, различием в поведении дислокаций в этих сплавах и позволяет выявить возможности расчетной модели. Так, в феррите и аустените фактор, тормозящий дислокации, — это сопротивление решетки (напряжение Пайерлса). В сорбитной структуре скольжение дислокаций определяется морфологией и распределением препятствий — карбидами Fe и Cr. В мартенсите движение дислокаций затруднено изначально. Таким образом, предметом исследования этой части работы фактически является структурный фактор.

Поскольку все исследованные материалы представляют собой сплавы на основе железа, их основные физико-механические характеристики отличаются не существенно. В расчетах использовались следующие значения: модуль упругости E = 186^218 ГПа; коэффициент Пуассона v = 0,20...0,31; модуль сдвига ц = 64^80 ГПа; вектор Бюргерса b = 2,5 - 10^-10 м. Данные численных экспериментов по реализации представленной модели и стендовых испытаний сплавов на основе Fe с различной структурной морфологией, в том числе и гетерогенных, приведены в табл. 1 и на рис. 1.

Таблица 1

Экспериментальные m0 и расчетные N3 значения числа соударений* для сплавов на основе Fe

Материал (структура)	Параметры структуры				Параметры соударения
					V 0 = 250 м/с; R 0 = 0,55 мм			V 0 = 340 м/с; R 0 = 0,32 мм
	Решетка ( М р )	« 1	D [м–6]	l [м–6]	Расчет		Эксп.	Расчет		Эксп.
					N 3	« 0	m 0	N 3	« 0	m 0
АРМКО Fe (феррит)	ОЦК (2,9)	0,5	100	3,0	2197	—	—	1187	—	—
08Х18Н10Т (аустенит)	ГЦК (3,06)	0,5	100	3,0	2446	0,253	9680	1322	0,154	8597
20Х13 (сорбит)	ОЦК (2,9)	2,0	100	0,35– 0,50	4655	0,280	16630	3742	0,254	14768
20Х13 (мартенсит)	Тетраг. (2,95)	0,02	0,01	0,01	9844	0,550	17861	5705	0,470	12140
*Представлены значения чисел капельных соударений, попадающих в одну точку (определяются в программном обеспечении испытательного стенда).

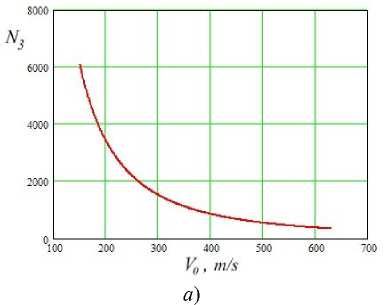
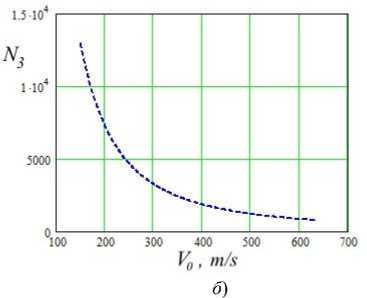
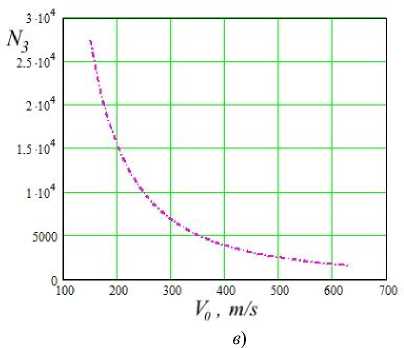
Рис. 1. Зависимости числа соударений N 3 , необходимых для зарождения трещин, от скорости соударения

V 0 при R 0 =0,55 мм для сплавов на основе Fe с различной структурой: феррит железа АРМКО ( а ); сорбит стали 20Х13 ( б );

мартенсит стали 20Х13 ( в )

Значения некоторых параметров, приведенных в табл. 1, нуждаются в пояснении. В качестве расстояния между препятствиями l на пути подвижных дислокаций в феррите и аустените принимается расстояние между дислокациями, то есть 1 = 1,JpJ . Учитывая высокую пластичность этих твердых растворов, плотность их дислокаций относительно невелика р d = 10¹¹ м^-2, что дает 1 ® 3 мкм. В закаленной стали плотность дислокаций близка к критической р kr = 10¹⁶ м^-2, что не только дает значение структурного параметра 1 ® 0,01 мкм в табл. 1, но и изменяет методику расчета числа соударений в исходной модели (1).

Для упрочненных металлических материалов (например, для сильно деформированных или закаленных сплавов, в том числе 20Х13 с мартенситной структурой), в выражении (1) первые три сомножителя обращаются в единицу. В таких материалах критическая плотность дислокаций р kr уже достигнута, поэтому понятие подвижных дислокаций р m теряет смысл. В численном виде это выражается так: р _k J p m = 1; V d = 0; D = 1 ₀ = 1/^p kr .

Что же касается экспоненты в выражении (1), то она сохраняет свой смысл со значениями параметров а 1 и 1, приведенными в табл. 1. Чтобы в такой структуре зародилась трещина, внешнему циклическому воздействию необходимо преодолеть существующие напряжения в насыщенной дислокационной среде и сформировать дефект сдвигового характера. Учитывая сказанное, расчетное выражение (1) для закаленной стали примет вид [23–26]:

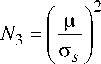
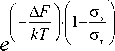
Здесь A F — энергия активации процесса преодоления препятствия без приложения внешнего напряжения, величина A F фактически определяет прочность препятствий с точки зрения прохождения их дислокацией; а _т — внутреннее напряжение, существующее в материале и позволяющее дислокации проходить препятствие при минимальных значениях A G . В качестве а_т принимается напряжение течения твердого тела при Т = 0К. Величины g _t и A F являются свойствами материала и в общем случае выражаются через его базовые физические характеристики ц и b :

g _t = ц ■ b 11 ; A F = a ■ ц ■ b ³ (3)

Машиностроение и машиноведение

Коэффициент α 1 в выражениях (3) классифицирует препятствия по их прочности [23].

В качестве напряжения σ s в выражении (2) рассматривается сдвиговое напряжение в плоскости скольжения, под действием которого происходит перемещение подвижных дислокаций. Напряжение σ s представляет собой проекцию вектора внешнего напряжения на плоскость скольжения и связано с системой скольжения решетки через фактор Тейлора М_р по закону Шмидта — Боаса для поликристалла [27]. Оно может быть выражено через параметры соударения V 0 и R 0 [28].

Экспериментальные значения, показанные в табл. 1, характеризуют инкубационный период эрозионного износа материала m 0 . Эта величина включает как стадию зарождения дефекта (трещины, поры, микрократеры), так и стадию его развития до начала потери массы образцом. Не представляется возможным инструментально выделить в экспериментальных величинах m 0 количество соударений, приходящихся только на стадию зарождения, поэтому значения N 3 являются исключительно расчетными. Вклад стадии зарождения в общее значение характеризуется коэффициентом α 0 = N 3 / m 0 .

Кроме численных значений, представленных в табл. 1, модель учитывает количество соударений N 3 , необходимое для зарождения очага разрушения (трещины, поры, микрократеры), и скорость соударений V 0 при фиксированных значениях размера капли R 0 . Кроме того, используя данное решение, можно определить зависимость N 3 от V 0 . Некоторые варианты таких зависимостей представлены на рис. 1.

Полученные результаты показывают, что расчетные данные N 3 не противоречат эксперименту (данным стендовых испытаний m 0 ). Они также демонстрируют соответствие базовым канонам механики разрушения. В частности, коэффициент α 0 характеризует энергию зарождения по отношению к энергии разрушения. В пластичных металлических материалах (АРМКО, аустенит, сорбит) энергия зарождения усталостных трещин существенно меньше энергии их роста. В упрочненных сплавах (мартенсит) энергия зарождения практически всегда выше энергии роста. Как правило, это соотношение значительно больше в пользу стадии зарождения. Данные табл. 1 показывают, что в стали 20Х13 с мартенситной структурой стадия зарождения усталостного дефекта N 3 составляет около половины всего инкубационного периода формирования износа m 0 : α 0 = 0,47 и 0,55 для скоростей соударения V 0 = 340 м/с и 250 м/с соответственно. Тогда как для той же стали с сорбитной структурой коэффициент α 0 вдвое меньше. Полученные нами значения α 0 соответствуют данным других авторов для аналогичных условий циклического нагружения (например, для стали 30ХГСН2А в [29]).

Расчетные зависимости на рис. 1 также соответствуют данным экспериментов. Они расположены асимптотически по отношению к значениям V 0 ≈ 100…150 м/с (проведенный численный эксперимент эту область подробно не исследовал). Названные выше расчетные зависимости соответствуют итогам стендовых испытаний, которые показали, что при V 0 < 135 м/с в сплавах на основе железа износ вообще не наблюдается [30– 34]. То есть асимптотичность графиков на рис. 1 подтверждает этот эмпирический факт: при указанных низких скоростях соударений не образуются усталостные дефекты критического размера.

Обсуждение и заключение. Не существует инструментальных методов точного определения продолжительности стадии зарождения очагов разрушения материалов, поэтому при необходимости используется предложенная расчетно-аналитическая модель. Она применима к материалам различной морфологии, в которых механизмы зарождения дефектов (трещин, пор, микрократеров) имеют дислокационную природу. Поэтому при нормальных условиях модель не применима к керамическим материалам с высокой долей ковалентных связей. Другим ограничением использования модели является, пожалуй, слишком высокая чувствительность экспоненциального множителя в выражениях (1) и (2). Небольшая погрешность при определении численных значений величин α 1 , σ s или l в этих формулах не позволяет получить результаты, адекватные экспериментальным данным. Выполненная работа дала важный прикладной результат — продемонстрировала, что целенаправленное конструирование структуры материала может существенно увеличить износостойкость.