Анализ надежности алгоритма программного обеспечения ортогональной структуры узловым методом

Любую программу можно описать алгоритмом, определяющим последовательность действий. Сам алгоритм в этом случае будет представлять собой некоторую структуру, элементами которой являются отдельные подпрограммы, блоки команд или непосредственно сами команды. При длительном жизненном цикле программы возникает проблема ее надежности, поскольку программы, как и радиоэлектронные устройства, также подвергаются сбоям. А с учетом того что все большую долю стоимости современных аппаратно-программных средств определяет именно программная часть, то в настоящее время особо важной становится задача разработки методов анализа надежности этих средств. Причем желательно получение не только конкретных численных результатов показателей надежности, но и таких соотношений, которые бы позволяли оптимизировать имеющийся алгоритм и даже синтезировать структуру с заданными характеристиками. С этой точки зрения достаточно большой интерес представляет тензорный метод анализа, разработанный Г. Кроном [1].

Сложная система состоит из некоторого числа простых элементов, каждый из которых характеризуется теми же параметрами, что и все остальные элементы. Для каждого отдельно взятого простейшего элемента действуют одни и те же законы. Поэтому представляется возможным анализ простой системы, являющейся элементом сложной системы, с последующим переносом полученных результатов на всю систему. Увеличение же числа элементов не приводит к появлению каких-либо новых физических явлений.

Рассмотрим применение тензорного метода анализа для исследования надежности алгоритмов программного обеспечения (ПО) и представим вариант получения системы уравнений для аналитических расчетов надежности программного обеспечения, позволяющий выбрать оптимальную структуру алгоритма при заданных характеристиках надежности [2].

Методика. Система простейшего типа состоит из одномерных членов (резисторов, узлов связи, блоков), соединенных в определенных точках; силы накладываются вдоль этих членов на узлы. Подобные структуры называют сетями. Предполагается, что накладываемые электромагнитные величины мгновенно распространяются через всю сеть, т. е. рассматриваемые сети имеют сосредоточенные, а не распределенные параметры.

Отметим, что хотя исследование сетей и производится автором на языке электротехники, следует подчерк- нуть, что используемая методология имеет отношение не только к методам электротехники. При изменении соответствующих выражений (например, «сила» вместо «напряжения») эта методология может также применяться при исследовании механических сетей [3]. Метод рассуждения в основном заимствован из таких разделов геометрии, как топология и дифференциальная геометрия. Математический аппарат, применяемый в рассмотрении технических задач, известен как тензорная алгебра и тензорный анализ. Изучение сетей предпринято таким образом, чтобы сформировать логический фундамент для познания более сложных технических структур, составные части которых имеют более одного измерения, соединение частей не сохраняется, а распространение воздействий не мгновенное [4].

Автор тензорного метода Г. Крон исходил из следующих предпосылок: если одна катушка характеризуется величинами е, i, R, L, С и Z, то множество катушек характеризуется и-матрицами е , i , R , L , С и Z [5]. Таким образом, множество катушек характеризуется тем же числом символов того же типа, что и одна катушка, но отличается тем, что отдельные числа заменяются и-матрицами различной размерности.

Следовательно, и-матрицы - это совсем не случайный набор каких угодно чисел. Компоненты каждой и-матрицы соответствуют некоторому определенному физическому (или геометрическому) понятию и в каждой задаче должно использоваться ровно такое количество и-матриц, сколько имеется в ней физических (или геометрических) понятий. Количество и-матриц может быть увеличено или уменьшено только в соответствии со строгими правилами, вытекающими из физической природы решаемой задачи.

В целом же сложные системы не только описываются тем же количеством символов, что и простые системы, но и весь метод рассуждения, используемый в анализе их поведения, соответствует этапам анализа простейших систем, отличаясь только тем, что вместо каждой величины используется и-матрица.

Этот рабочий прием, дающий экономию умственных усилий, называется постулатом первого обобщения и может быть выражен таким образом: метод анализа и окончательные уравнения, описывающие поведение сложной физической системы (с и степенями свободы), могут быть найдены последовательно при анализе простейшего, но наиболее общего элемента (unit) системы при условии, что каждая величина заменяется соответствующей и-матрицей. Простейший элемент системы может иметь одну или несколько степеней свободы [1].

В силу того что действия с и-матрицами почти не отличаются от действий с обычными величинами, при параллельном анализе обычные величины мы будем записывать в видоизмененной форме:

• -    вместо деления на число, например 1/Z, будем умножать на Z^-1, что соответствует матрице Z^-1, являющейся обращенной матрицей Z;

• -    вместо возведения числа в квадрат, например Z², будем записывать эту операцию как умножение Z ■ Z, что соответствует матричной записи произведения матриц Z ■ Z;

• -    все величины, которые получаются в определенном порядке в процессе анализа, должны записываться в том же строгом порядке, если предполагается использовать и-матрицы в прямом обозначении. Если используется индексное обозначение и в выражениях отсутствуют операторы, т.е.р = d / dt, то порядок записи не играет роли.

Введенные выше правила обращения с обычными величинами почти совпадают с правилами обращения с операторами типaр = d / dt.

Следует отметить, что каким бы методом ни были получены окончательные уравнения, для получения решения в численном виде всегда требуется определенное количество сложений и умножений. Однако часто наблюдается, что окончательный ответ, получаемый с помощью и-матриц, имеет значительно более организованную форму чем ответ, выраженный через обычные величины, и, следовательно, требует меньшего количества вычислений, а благодаря организации данных численные расчеты могут быть выполнены вычислительной машиной. Кроме того, использование и-матриц предлагает новый подход, который не вытекает из обычных соображений, и окончательный ответ получается в новой форме, требующей намного меньше вычислительной работы [5]. Таким образом, использование и-матриц в общем случае дает экономию в аналитической и вычислительной работе.

Организация множества величин в одну и-матрицу и представление последней с помощью одной базовой бук- выЛ является чем-то несравненно большим, чем стенографическое обозначение и эффективный рабочий прием. Организация множества величин в и-матрицу и одновременное введение таких понятий, как преобразование, инвариантность и группа, означает творение принципиально новой математической сущностиЛ, обладающей такими свойствами, которые отсутствуют в образующих ее строительных блоках: в и-матрицах или их компонентах. Созидание посредством организации новых сущностей из простого набора и-матриц и наделение этих сущностей новыми свойствами и составляет основную цель тензорного анализа.

Создание новых математических сущностей и наделение их новыми свойствами эквивалентно открытию в описываемых физических (или геометрических) явлениях новых физических (или геометрических) сущностей, подчиняющихся новым физическим законам.

Следует особенно подчеркнуть, что и-матрицы сами по себе не являются новой математической сущностью. Таким образом, факт представления токов в системе одним символом z, напряжений - символом е и импедан-сов - символом z не является созиданием новых сущностей, так же и как способ представления тока в виде точки в и-мерном пространстве. Сама и-матрица - просто стенографическая запись и эффективный рабочий прием -не обладает ни одним свойством, которого бы не имели ее компоненты. И и-матрицы, и их компоненты имеют одни и те же правила действий над ними: их можно суммировать, умножать, дифференцировать и т. п. Использование и-матриц можно сравнить с использованием экскаватора там, где работало много рабочих с ломами и лопатами.

Для того чтобы наделить и-матрицы новыми свойствами, которыми они не обладали ранее, и тем самым создать новую математическую сущность, необходимо ввести новое содержание в матричное уравнение, которым не обладают обычные уравнения. Это новое содержание вводится с помощью трех взаимосвязанных понятий: преобразование, инвариантность и группа. Вместе с тем отметим, что введение новых понятий и нового содержания возможно и без обязательного использования и-матриц.

Одной из целей тензорного анализа при анализе любой физической проблемы является введение такого количества символов, которое соответствует количеству физических сущностей, участвующих в естественном явлении, и такого количества связей (отношений) между ними, которое имеется в наблюдаемом явлении. Таким образом, в уравнениях тензорного анализа каждый математический символ (базовая буква) соответствует физической или геометрической сущности, а каждая операция над символами - физическому или геометрическому отношению, имеющему место между сущностями.

Постулат второго обобщения утверждает, что одному и тому же символу А соответствует не одна и-матри-ца, а очень большое количество и-матриц, каждая из которых имеет одну и ту же размерность, одно и то же число осей, но отличаются значениями компонент.

Теперь каждый символ или базовая буква означает бесконечное число и-матриц, которые образуют новую математическую сущность, называемую геометрическим объектом. Каждая частная и-матрица будет записываться со скользящими индексами (снабженными одним или двумя штрихами), закрепленными за базовой буквой. Это означает, что с каждым геометрическим объектом в каждой частной системе координат связана и-мат-рица, которая дает значение компонент одного и того же геометрического объекта в этой частной системе координат. Если система координат изменяется, то изменяются и компоненты геометрического объекта, идентифицируемые штрихами индексов, но сам геометрический объект остается неизменным, что представлено неизменной базовой буквой.

В физических явлениях геометрический объект соответствует физическому объекту, такому как вектор скорости движущегося тела или напряжения в деформированном теле. Следовательно, выражение «геометрический объект», используемое для А_аЬс, с таким же успехом можно заменить на «физический объект» или на «математический объект».

Итак, компоненты, скажем, вектора скорости v^a некоторой точки, измеренные в одной частной системе координат, дадут значения va' , измеренные в другой системе v a ‘ , ав третьей - v a ит.д.И хотя все эти компоненты могут быть различными, но сама скорость точки остается неизменной.

Представление геометрического объекта в частной системе координат состоит не только из значений компонент, расположенных в строку, квадрат или куб, но и из фиксированных индексов, закрепленных по сторонам и-матрицы. Это означает, что когда даются компоненты геометрического объекта, необходимо указать систему ко ординат, в которой эти компоненты имеют данные численные значения. Если фиксированные индексы, указывающие оси этой частной системы, изображаемые рядом с компонентами, опущены, то в данном случае это и-матрица, имеющая заданные компоненты, а не геометрический объект [6]. Например, понятие «матрица» относится к множеству величин, расположенных в виде прямоугольника, а не к фиксированным индексам, расположенным вдоль сторон прямоугольника.

Введение новой сущности - геометрического объекта - вместо и-матрицы вводит и новую терминологию и новые обозначения. Причина каждого такого изменения устанавливается по мере непрерывного развития новых понятий.

Для того чтобы математически представить один геометрический (или физический) объект, необходимо показать все его компоненты во всех возможных системах координат Это означает, что полное математическое описание геометрического объекта возможно лишь очень большим, обычно бесконечным числом и-матриц. На практике это описание осуществляется следующим образом:

• -    из бесконечного множества и-матриц выбирают только одну и полностью ее задают, показывая значение всех ее компонент;

• -    кроме того, задают частную систему координат, в которой определено значение всех компонент этой и-матрицы;

• -    определяют все возможные системы координат, в которых геометрический объект может представляться и-матрицей;

• -    указывают формальную процедуру, или формулу посредством которой можно найти все другие матрицы в других системах координат.

Экспериментальная часть. Рассмотрим пример использования узлового метода анализа надежности алгоритма программного обеспечения ортогональной структуры, состоящей из семи ветвей (рис. 1). Для того чтобы не загромождать рисунок, возле каждой ветви приведен лишь ее номер, который подставляется в индексы i соответствующих величин Kg.,f. и Z..

Параметры структуры исходного алгоритма следующие:

• - и = 7 - число ветвей;

• -    U= 7 - число функциональных блоков;

• - К=1 - число подалгоритмов;

• -    (и - k) = U-К = 7 - 1 = 6 - число узловых пар;

• -    к = и - (и - k) = 7 - 6= 1 - число контуров.

Кроме интенсивностей поступающих потоков, в качестве известных величин выступают заданные величины времени наработки на отказ в ветвях 4, 5, 6.

На первом этапе узлового анализа ортогональной структуры алгоритма необходимо произвести выбор закрытых путей и преобразовать их в открытые. Число закрытых путей в сети равно числу контуров. В рассматриваемом алгоритме присутствует только один контур. Далее этот контур открывается и в месте разрыва вводится мнимая ветвь. В образовавшихся семи узловых парах выбираются произвольные направления совокупных величин времени наработки на отказ (рис. 2).

Также приведем структуру примитивной узловой схемы, которая будет использоваться в качестве вспомогательной (рис. 3).

На втором этапе нужно установить геометрические объекты и уравнения состояния.

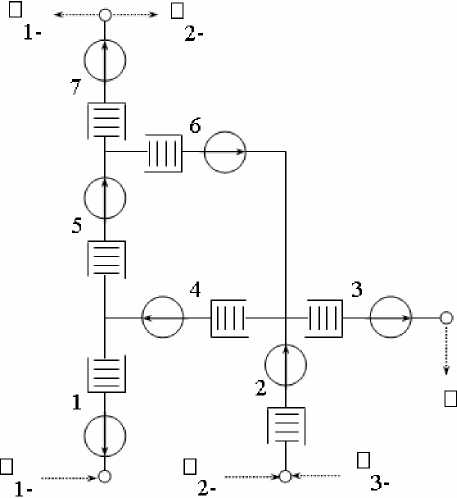
Рис. 1. Исходный алгоритм ортогональной структуры

-/- квадратная матрица размерностью и строк на и столбцов. Элементы главной диагонали представляют собой значения интенсивности выхода потока отказов из функциональных блоков, соответствующей данной ветви. Остальные элементы матрицы отражают взаимное косвенное влияние функциональных блоков друг на друга (использование общих ресурсов и т. д.). В данном примере косвенное влияние между функциональными бло-

ками отсутствует, поэтому все недиагональные элементы матрицы/равны нулю [6]:

. f=

. /1,1	0	0	0	0	0	0
0	. / г.г	0	0	0	0	0
0	0	. / з.з	0	0	0	0
0	0	0	. /4,4	0	0	0
0	0	0	0	. /5.5	0	0
0	0	0	0	0	. f6.6	0
0	0	0	0	0	0	. fl.

.

1 а

Kg =

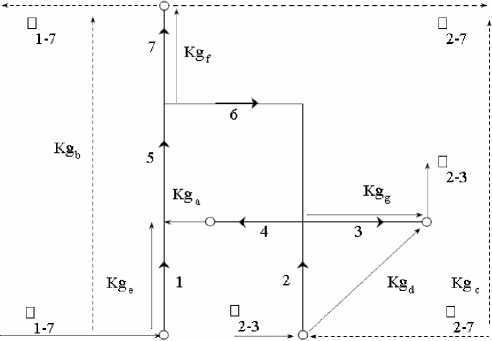
Рис. 2. Схема замещения исходной ортогональной схемы узловой схемой (функциональные блоки в ветвях схематически обозначены стрелками, указывающими направление обслуживания)

⎡_⎢ Kg 1 ⎤_{⎥ ⎢} Kg _{2 ⎥} ⎢_⎢ Kg 3 ⎥_⎥ ⎢ Kg ₄ ⎥ ^⎢_⎢ Kg ₅ ^⎥_⎥ ⎢_⎢ Kg 6 ⎥_⎥ ⎣ Kg ₇ ⎦

⎡^λ 1 ⎤

⎢_{⎢λ 2} ⎥_⎥

,

λ=

λ λ λ λ

.

7 ⎦

Матричное уравнение состояния примитивной структуры будет

X = f • Kg .                    (1)

На третьем этапе определяется тензор преобразо

вания.

Выражения коэффициентов готовности в ветвях примитивной схемы алгоритма через совокупные коэффициенты готовности в открытых контурах преобразованной исходной сети имеют вид

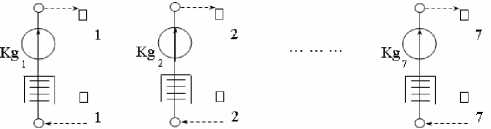
Рис. 3. Структура примитивной узловой схемы алгоритма из семи ветвей

Kg 1 = Kg_{e )}

Kg ₂= Kg_d - Kg_s ,

Kg 3 = Kg g ,

Kg 4 = - Kg_a - Kg_b + Kg_c - Kg d + Kg , + Kg g , Kg ₅= Kg₆ - Kg , - Kg_{/ ;}

Kg ₆ = - Kg_c + Kg d + Kg / - Kg g ,

Kg , = Kg_{/ )}

a b c \d , If g

-1

A = -1

-1

-1

-1

-1

-1

1 0

-1

0   0

0    1    0

На четвертом этапе находятся геометрические объекты, соответствующие исходной схеме.

Интенсивность потоков отказов в открытых путях исходной схеме алгоритма определяется по формуле

λ′ = A^T ⋅λ=

Геометрические объекты, необходимые для описания примитивной схемы алгоритма (в соответствии с постулатом первого обобщения), будут следующими:

• -    X - вектор, компоненты которого представляют собой интенсивности потоков отказов, протекающих в соответствующих ветвях;

• -    Kg - вектор, компоненты которого представляют собой коэффициенты готовности функциональных блоков в соответствующих ветвях;

	0	0	0	-1	0	0	0		Х 1		-Х 4
	0	0	0	-1	1	0	0		Х г		—Х4 + Х 5
	0	0	0	1	0	-1	0		Х 3		Х 4 - ^ 6
	0	1	0	-1	0	1	0		Х4	=	^ 2 — Х4 + ^ 6
	1	0	0	1	-1	0	0		Х 5		Х 1 + Х 4 - Х- 5
	0	0	0	0	-1	1	1		Х б		-^ 5 + Х б + Х 7
	0	-1	1	1	0	-1	0		N		-Х г + Х з + Х 4 -Х б

Штриховая линия разделяет матрицу X’ на две подматрицы:

	⎡-λ 4 + λ 5          ⎤
	⎢λ 4 -λ 6
<   <>	⎢⎢λ 2 -λ 4 +λ 6 ⎢λ 1 +λ 4 -λ 5 ⎢⎢-λ 5 +λ 6 +λ 7 ⎢⎣-λ 2 +λ 3 +λ 4 -λ 6 ⎦	(2)

Значения интенсивности выхода потока отказов из функциональных блоков в открытых путях исходной схемы находятся по формуле f ‘ = AT • f • A. (3)

В целях экономии места применяется следующее правило: при умножении любой матрицы М на диагональную (если такое умножение возможно) эта матрица сохраняет свою размерность, а каждый ее ненулевой элемент M i , j умножается на диагональный элемент T j , j в соответствующем столбце [5].

Чтобы не загромождать текст промежуточными выкладками, приведем результирующее значение матрицы f' :

	/ 4	Т4	■ 4	74	■74	0	■ 4
	Т4	/4 + / 5	■ 4	/4	■ f 4 ■ f 5	■/ 5	■ 4
	■/ 4	■ 4	/4+/б	■ 4 ■Тб	/ 4	■7 6	Т4 +Т6
f '=	Т4	Т4	■ 4 ■Тб	/2 + / 4 + / б	■74	Тб	■ 2 ■_/ 4 ■Тб
	■ 4	■ 4 ■Тб	Т4	■74	/1 + 74 + / 5	/5	Т4
	0	■Т5	■Тб	Тб	/5	/5 + / 6 +/,	■Т б
	■ 4	■ 4	74 +Тб	■ / 2 ■./ 4 ^Тб	Т4	■/ 6	Т2 +Т3 +Т4 +7б

Штриховые линии делят матрицу f' на четыре подматрицы:

/ш    /4 t

7(3)

7(2) = | 74   "Т А 74   ~ f 4   0   ^ 4 |,

■ / 4

■ / 4 0

■ / 4

	Т4 +Т5	■4	Т4	■ / 4■_ / 5	■/5	■4
	■4	Т4+ Тб	■Т4 ■Тб	Т4	■б	Т4 +Тб
А) =	Т4	■4 ■Тб	Т2 +Т4 +Тб	■Т4	Тб	■ / 2 ■Та ■Тб
	■A - f s	Т4	■Т4	Т1 +./ 4 +Т 5	Т5	Т4
	■ / 5	■б	Тб	Т5	Т5+Тб+/7	■б
	■4	Т4 + Тб	■2 ■ТА^Тб	Т4	■б	Т2 + Т3 + Т4 + 7б

На пятом этапе находится уравнение состояния исходной схемы алгоритма.

λ _{k 1} +λ _{y 1} = f ₁ ( Kg_{k 1} + Kg_{y 1} ) + f ₂ ( Kg_{k 2} + Kg_{y 2} ), λ k 2 +λ y 2 = f 3 ( Kg k 1 + Kg y 1 ) + f 4 ( Kg k 2 + Kg y 2 ).

Поскольку рассматриваемая ортогональная схема приведена к узловой, то следующие матрицы обращаются в нуль:

Kg y 1 = 0, Kg k 2 = 0, λ k2 = 0, λ y1 = 0.

Тогда система уравнений исходной схемы алгоритма записывается как

⎧⎪λ _{k 1} = f ₁ ⋅ Kg_{k 1} + f ₂ ⋅ Kg_{y 2} , ^⎨⎪_⎩λ y 2 = f 3 ⋅ Kg k 1 + f 4 ⋅ Kg y 2 .

Вектор совокупных очередей в открытых контурах и его составляющие имеет следующий вид:

	Kg' a
	Kg b		Kg b
	Kg ’		Kg ’
Kg ' =	Kg' d	Kg ki 1 = Kg ’ [ Kg y 2 =	Kg' d
	Kg ’		Kg ’
	Kg f		Kg f
	Kgg		Kgg

На шестом этапе в зависимости от условия задачи после решения системы уравнений необходимо воспользоваться формулами для расчета интенсивностей потоков сообщений и среднего времени наработки на отказ в ветвях исходной схемы алгоритма:

Kg_{y 2} = ( f ₄ ) ^{- 1} ⎢_⎣λ _{k 2} +λ _{y 2} - f ₃ ( Kg_{k 1} + Kg_{y 1} ) ⎥_⎦- Kg_{k 2} , λ k 1 = f 1 ( Kg k 1 + Kg y 1 ) + f 2 ( Kg k 2 + Kg y 2 ) -λ y 1 .

В результате вычисления по этим формулам получаются величины интенсивностей контурных потоков отказов в исходной схеме алгоритма и совокупные коэффициенты готовности в открытых путях, при помощи которых находятся интенсивности потоков отказов или требуемые наработки на отказ в ветвях.

На основании вышеизложенного можно сделать вывод о том, что тензорный метод анализа является эффективным при исследовании характеристик надежности алгоритмов программного обеспечения.

Таким образом, автором был проведен анализ существующих методов исследования надежности программного обеспечения, определен новый подход к исследованию надежности алгоритмов программного обеспечения на основе тензорной методологии и предложены основные пути по его реализации.