Анализ надежности при планировании реконструкции тяговой подстанции на основе теории нечетких множеств

Железнодорожный транспорт представляет собой сложную техническую систему. Одним из показателей эффективности функционирования такой системы является надежность.

Согласно «Стратегии развития железнодорожного транспорта в Российской Федерации до 2030 года» [1] предусматривается ввод новых и реконструкция существующих тяговых подстанций, строительство новых линий контактной сети. На этапе проектирования расчет показателей надежности тяговой подстанции осуществляется в основном классическими методами [2-4] на основе составления структурных схем и использования статистических значений показателей надежности отдельных элементов. Краеугольным камнем большинства методов оценок надежности служит еще и тот факт, что зачастую за исходные показатели надежности принимают значения показателей надежности нового оборудования, что не является обоснованным в процессе эксплуатации и планировании реконструкции тяговой подстанции.

В системах тягового электроснабжения (СТЭ) есть два типа неопределенности: случайность и нечеткость [5]. Вероятностные модели могут использоваться для случайности, но не для нечеткости. На практике при анализе надежности вариантов реконструкции тяговых подстанций из-за неточности и неполноты исходных данных оценка точных значений показателей надежности становится затруднительной. Лица, принимающие решение (ЛПР), в таких случаях рассматривают приближенные значения показателей, а доверительные границы таких показателей надежности могут отличаться от реальных значений. Принимая во внимание неопределенность и неполноту сведений об условиях эксплуатации конкретного электрооборудования, представляется обоснованным использовать модели надежности с нечеткими параметрами [5, 6]. Нечеткие модели становятся необходимым дополнением к вероятностным моделям, чтобы учесть оба вида неопределенности исходных данных при вероятностном планировании реконструкции и модернизации тяговой подстанции.

Вышесказанное делает актуальным разработку и совершенствование методов анализа надежности тяговой подстанции при реконструкции в условиях неопределенности.

Один из методов, который позволяет вычислить показатели надежности в условиях неопределенности, основан на применении теории нечетких множеств (ТНМ) [5, 7]. В работах [8-11] были разработаны методы с применением так называемых треугольных нечетких чисел (ТНЧ), представляющих собой нечеткие числа с функцией принадлежности (ФП) в треугольном виде. ТНМ – математический аппарат для работы с объектами, не имеющими жестких, однозначно задаваемых границ. Он позволяет формально описывать нестрогие, нечеткие, расплывчатые понятия и производить с ними различные операции.

На основе ТНЧ предлагается определить показатели надежности элементов тяговой подстанции, что позволит на основе этих показателей в сочетании с методом минимальных се-– 53 – чений отказов [12] выполнить анализ надежности схемы электрических соединений тяговой подстанции в условиях неопределенности.

Понятие нечеткого числа и правила операций

Пусть U – традиционное множество и его член обозначается как x . Нечеткое множество A по U определено как ряд упорядоченных пар и выражается в виде

A = {( x ,ц A ( x )| x e U },                                                  (1)

где µ_A( x ) – ФП элемента к множеству A , изменяющаяся от 0 до 1.

Равенство µ A ( x ) = 1 означает, что x точно принадлежит множеству A ; равенство µ A ( x ) = 0 говорит о том, что x точно не принадлежит множеству A. Нечеткие множества отличаются от обычных множеств тем, что допускают промежуточные значения функции принадлежности, например, µ _A ( x ) = 0,5.

В частности, A – вероятностное нечеткое множество, если µ A ( x ) является случайной переменной, определенной на вероятностном пространстве.

A α , называемое α сечением A , определяется как

A _a = {( x g U |ц a ( x) >  a , 0 <  a <  1,}.                                     (2)

Нечеткое число – специальный тип нечеткого множества. Нечеткое число определяется как выпуклое, нормализованное нечеткое множество с кусочно-непрерывной ФП [13]. Согласно этому определению очевидно, что α сечение A _α нечеткого числа A является интервалом с нижней и верхней границей при a l (α) ≤ a u (α). Очевидно, что a l (α) и a_u (α) – монотонно убывающая функция α . И нижняя, и верхняя границы соответственно. Поэтому операции нечетких чисел могут быть выполнены по правилам вычисления интервалов.

Для двух заданных нечетких чисел A α = [ a l (α), a u (α)] и B α = [ b l (α), b u (α)] могут применяться следующие правила операций.

Суммирование

	( A + B ) a	= [ a l (a) + b l И a u (a) + b u (a ) ].	(3)
Вычитание
	( A — B X	= [ a i (a) - b i (a) , a u (a) - b u («) ]•	(4)
Умножение
	( AB X =	min a i (a) • b i (a) , a u (a) • b i (a) , a i	(a) • b u (a) , a u (a) • b u (a)), l .         (5)
	α	max( a i (a) • b, (a), a u (a) • b, (a), a	(a) • b u (a) , a u (a) • b u (a)) .

Если A и B определены на положительном монотонном пространстве вещественных чисел, то (5) становится

(ABX = [at (a) ■ b H au (a) ■ bu (a)] .                                     (6)

В частности, если H – положительное постоянное число, то

(HA )a = [Hal (a), Hau (a)J

Деление

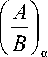
= [al H, au (a)]-

где b l (α) ≠ 0 и b u (α) ≠ 0 . Иначе, один или оба конца интервала расширяются до ∞.

Для практических вычислений удобно работать с нечеткими числами специального вида [5, 10].

Треугольное нечеткое число, которое часто обозначается как A =( a₁,a₂,a₃ ), определено следующей ФП (рис. 1):

	( x - a i )/(a 2	- a i )	если	a i ^ x ^ a 2
P A (x ) ='	( a - x ) /( a 33	- a 2 )	если	a 2 <  x <  a 3
	0		если	x <  а 1 или x >  а 3

Вычисление α сечения A _α треугольного нечеткого числа

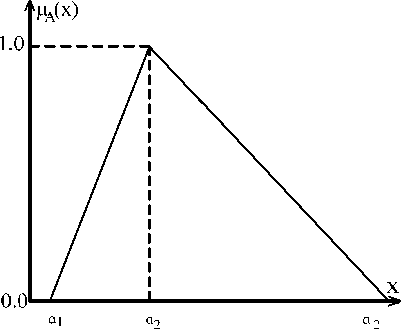
Рис. 1. ФП треугольного нечеткого числа

Fig. 1. Membership functions of a triangular fuzzy number

Определение нечетких показателей надежности

Элементы СТЭ классифицируются на две категории: с восстановлением и без восстановления. Элемент системы электроснабжения является восстанавливаемым в течение нормального периода эксплуатации и может выйти из строя в конце срока эксплуатации. Полнота исходной информации зависит от нескольких факторов [13]. По ряду показателей актуальная информация может отсутствовать [6, 14, 15].

Среднее выборки времени восстановления может быть легко вычислено как среднеарифметическое времени восстановления при различных событиях отключений

1 ⁿ

τ = _n ∑ _{t =} τ i , (11) где τ – точечная оценка времени восстановления (в часах); τ _i – время i -го восстановления; n – число восстановлений в статистических отчетах.

Доверительный интервал ожидаемого времени восстановления может быть оценен по критериям t -распределения или нормального распределения [5, 10].

Метод оценки следующий. Предполагается, что β представляет реально ожидаемое время восстановления, a s – среднеквадратичное времени восстановления по выборке. Если используется критерий t -распределения, то можно подтвердить, что для данного существования уровня α случайная переменная (τ–β) n / s расположена между – t α ( n –1) и t _α( n –1) с вероятностью 1–α , где t _α( n –1) – такое значение, что интеграл функции плотности t -распределения c ( n –1) степенями свободы от t α ( n –1) до ∞ равняется α . Поэтому мы имеем

- t α ( n - 1) ≤

(τ - β) s / n

≤ t _α( n - 1).

Средняя интенсивность отказов отдельных компонентов не может быть получена как среднее выборки из отчетов по отказам. Интенсивность отказов оценивается как среднее число отказов за год в течение рассматриваемого периода времени T :

λ = ⁿ , T

где λ – точечная оценка интенсивности отказов (отказов/год); n – число отказов элемента за рассматриваемое время T (в годах), которое представляет все прошедшее время минус полное время отключений из-за отказов. В большинстве случаев полное время отключений – очень малая часть и T может быть аппроксимировано всем прошедшим временем, в течение которого рассматриваются события отказов. Это подразумевает, что интенсивность отказов аппроксимирована частотой отказов.

Доверительный интервал ожидаемой интенсивности отказов может быть оценен следующим методом. Согласно теории статистики существуют следующие соотношения между распределением χ ² (хи-квадрат) и распределением Пуассона:

χ ² (2 N ) = 2λ T .

Здесь λ – ожидаемая интенсивность отказов, T – весь рассматриваемый период времени, N – число отказов за время T.

Уравнение (14) указывает, что двукратная величина отказов в течение времени T следует распределению хи-квадрат с 2N степенями свободы. Поэтому для заданного уровня значения α можно утверждать, что интенсивность отказов λ относится к следующему случайному до, верительному интервалу с вероятностью 1–α:

xU'²N )<, < .x2NN ) л —------- S л s------

2 T           2 T

Вычисления нечетких чисел, по существу, связаны с обнаружением точных верхней и нижней границ нечеткой функции [10]. При необходимости с помощью экспертов может быть получена более консервативная (более широкая) интервальная оценка [8].

Коэффициент простоя для восстанавливаемого j -го элемента равен

- ( X , ) . . (t , ) . ,, ;X j "T j ") (16)

I M a отказов, записанное в виде (λj)α = ( λj’, λ j , λj”), с ниж

q ( t ) α

(λ ) α

(ЧЭа +

Л

к

где (λ j ) α – нечеткое

число интенсивности

ней границей λ j ’, средним значением λ _j и вер х ней границей λ j ”; (τ j ) α – нечеткое число времени во сстановления, записанное в виде (τ j )_α = (τ j ’, τ _j , τ j ”), с нижней границей τ j ’, средним значением τ j и верхней границей τ j ”.

Минимальное сечение отказов (МСО) определяется как набор элементов, отказ которых приводит к отказу системы, но если любой элемент сечения остается работоспособен, отказа системы нет. системынет.

В большинстве методов с использованием МСО часто принимают два вида приближений:

n к              мт

• 1)    нет необходимости перечислять все МСО, так как вероятности отказов элементов в целом малы и, таким образом, вероятность появления сечений более высокого порядка может быть очень низкой, т.е. МСО более высокого порядка могут быть проигнорированы в перечислении;

• 2)    вероятности пересечений двух и более МСО во многих случаях обычно чрезвычайно низки, и поэтому влияния невзаимного исключения среди МСО незначительны.

Каждое МСО составлено из параллельных элементов, если для отказа набора должны отказать все элементы в наборе. Совокупность МСО соединена последовательно, если для отказа системы достаточно отказа только одного из них. Поэтому для модели системы может использоваться комбинация МСО последовательно и элементов каждого сечения параллельно.

ФП множества показателей для каждого МСО вычисляют, используя формулы надежности для параллельной и последовательной сети и правила операций для нечетких чисел [10].

МСО в расчетной схеме реализуется, если все исходные события (отказы элементов) А 1 … А_n происходят в нем. Вероятность возникновения i -го МСО в момент времени t , ( q_i* ( t ))_α получаем при пересечении (конъюнкции) отказов элементов [12]:

(qi∗(t))α=P((Ai)α⋅(Aj)α), где (Ai)α – i-е минимальное сечение, выраженное нечетким числом.

Показатель ω i *( t ) – ожидаемое число появлений i -го МСО в единицу времени в момент t – определяется выражением

(ωi∗(t))α=∑(ωj';ωj;ωj")∏(qi';qi;qi"), j=1

l≠j где (ωj(t))α – нечеткое число, параметр потока j-го исходного события в i-м МСО, n – число членов МСО.

Показатель (λ_i*( t )) _α – интенсивность появления i- го МСО – определяется через показатели ( ω i * ( t )) α и ( q i ( t )) α :

∑ ( ω j '; ω j ; ω j ") ∏ _l ( q i '; q i ; q i ")

( ω i ^∗ ( t ) ) α     ₌ ^{j = 1}                     l ≠⁼ j

[ 1 - ( q i ^∗ ( t ) ) α ]           [1 - P (( A i ) α ⋅ ( A j ) α )]

Коэффициент простоя тяговой подстанции ( q_с ( t ))_α – вероятность того, что конечное событие отказа подстанции существует в момент t , т.е. вероятность отказа тяговой подстанции определяется по выражению

N МСО

( q с ( t )) α = ∑ _{i = 1} ( q i ( t )) α ),                                                           (20)

= где Nмсо- общее число МСО.

Интенсивность отказа тяговой подстанции (Λ с ( t )) α , или вероятность того, что конечное событие произойдет в единицу времени в момент времени t при условии, что оно не существует в момент t ,

N

( Λ c ( t )) α = ∑ (λ i ^∗ ( t )) α . (21) i = 1

ФП интенсивности отказов и времени восстановления элементов могут быть созданы по точечным и интервальным оценкам интенсивности отказов и времени восстановления соответственно. ФП коэффициента простоя элемента может быть получена по функциям принадлежности λ и τ.

Пример. Рассмотрим схему открытого распределительного устройства 110 кВ тяговой подстанции, показанную на рис. 2. В процессе реконструкции подстанции предлагается взамен устаревших масляных выключателей установить современные и более надежные элегазовые

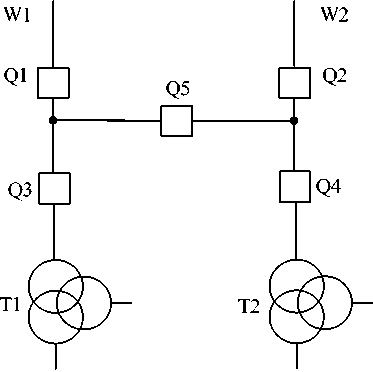
Рис. 2. Схема ОРУ 110 кВ тяговой подстанции

Fig. 2. 110 kV open switchgear circuit of a traction substation

– 58 – аппараты. Средние значения и доверительные границы интенсивности отказов и времени восстановления электрооборудования тяговой подстанции представлены в табл. 1.

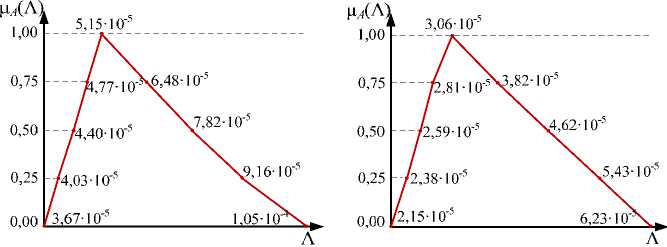
Значения нижней и верхней границ коэффициента простоя и интенсивности отказов тяговой подстанции, соответствующие пяти точкам функции принадлежности, даны в табл. 2 и 3 соответственно. В результатах использо вал и шаг 0,25. Шаг может быть выб ра н в зависимости от требований точности при вычислении ФП.

Для двух вариантов схем тяговой подстанции с масляными и элегазовыми выключателями функции принадлежности показаны на рис. 3 и 4.

Анализ функций принадлежности показателей надежности (рис. 3, 4) показал, что применение элегазовых выключателей при реконструкции схемы тяговой подстанции приводит к повышению надежности ее в части уменьшения коэффициента простоя и интенсивности отказов.

Таблица 1. Средние значения и доверительные границы интенсивности отказов и времени восстановления электрооборудования тяговой подстанции

Table 1. Mean values and confidence limits of failure rate and recovery time of electrical equipment of traction substation

Интенсивность отказов
Элемент схемы	Буквенное обозначение	λ H , 1/год	λ B , 1/год	λ , 1/год
Линия (5 км)	W1, W2	0,072	0,1	0,08
Трансформатор	T1, T2	0,012	0,02	0,014
Масляный выключатель	Q1, Q2, Q3, Q4, Q5	0,014	0,02	0,016
Элегазовый выключатель	Q1, Q2, Q3, Q4, Q5	0,0045	0,00625	0,005
Время восстановления
Элемент схемы	Буквенное обозначение	τ H , г	τ B , г	τ , г
Линия (5 км)	W1, W2	0,00153	0,00212	0 , 0017
Трансформатор	T1, T2	0,00679	0,011	0,00799
Масляный выключатель	Q1, Q2, Q3, Q4, Q5	0,00414	0,00575	0,0046
Элегазовый выключатель	Q1, Q2, Q3, Q4, Q5	0,00205	0,00285	0,00228

Таблица 2. ФП коэффициента простоя системы

Table 2. The membership functions of the ratio of system downtime

Точка принадлежности	ТП с масляными выключателями		ТП с элегазовыми выключателями
	Нижняя граница	Верхняя граница	Нижняя граница	Верхняя граница
1	7,89∙10-8	7,89∙10-8	3,78∙10-8	3,78∙10-8
0,75	7,15∙10-8	1,14∙10-7	3,40∙10-8	5,64∙10-8
0,5	6,35∙10-8	1,48∙10-7	3,02∙10-8	7,51∙10-8
0,25	5,60∙10-8	1,84∙10-7	2,64∙10-8	9,39∙10-8
0	4,76∙10-8	1,05∙10-7	2,26∙10-8	1,13∙10-7

Таблица 3. ФП интенсивности отказов системы

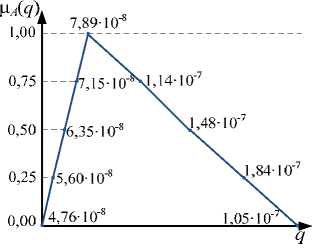
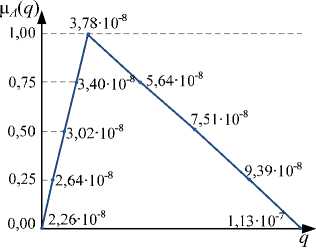
Table 3. The membership function of the failure rate of the system

Точка принадлежности	ТП с масляными выключателями		ТП с элегазовыми выключателями
	Нижняя граница	Верхняя граница	Нижняя граница	Верхняя граница
1	5,150∙10-5	5,150∙10-5	3,060∙10-5	3,060∙10-5
0,75	4,770∙10-5	6,480∙10-5	2,810∙10-5	3,820∙10-5
0,5	4,400∙10-5	7,820∙10-5	2,593∙10-5	4,618∙10-5
0,25	4,033∙10-5	9,155∙10-5	2,376∙10-5	5,433∙10-5
0	3,668∙10-5	1,053∙10-4	2,148∙10-5	6,233∙10-5

а)                                           б)

Рис. 3. ФП коэффициентов простоя для тяговой подстанции с масляными (а) и элегазовыми (б) выключателями

Fig. 3. Th function of the ratio of downtime for traction substation with a) ilb eakers switchgear a d б SF6 breaker witchgear

а)                                           б)

Рис. 4. ФП интенсивности отказов для тяговой подстанции с масляными (а) и элегазовыми (б) выключателями

Fig. 4. The membership function of the failure rate for traction substations from a) oil breakers switchgear and б) SF6 breakers

Заключение

Предложена методика анализа надежности при реконструкции тяговой подстанции на основе теории нечетких множеств, позволяющая оценить показатели надежности в условиях нечеткой информации исходных данных и принять обоснованный вариант реконструкции. Такой подход является актуальным при реконструкции тяговых подстанций железных дорог, когда объема исходных данных, используемых для оценки надежности, недостаточно. Показатели надежности элементов СТЭ могут быть описаны треугольными нечеткими числами.

Используемый метод построения функций принадлежности повышает эффективность решения задач оценки надежности тяговой подстанции для разного состава электрооборудования при выборе варианта реконструкции тяговой подстанции.