Анализ напорной характеристики центробежных компрессорных рабочих колес

Для решения прямой задачи – расчета газодинамических характеристик ступени центробежного компрессора – и обратной задачи – проектирования ступени на заданное отношение давлений – достаточно преодолеть основные трудности, а именно рассчитать подводимую к газу механическую работу и ту ее долю, которая идет на преодоление сопротивления движению газа в проточной части [1].

В безразмерном виде задача сводится к расчету коэффициента теоретического напора ^, = c«г / U (где С_и2 — окружная составляющая абсолютной скорости на выходе из рабочего Tu 22    u2

колеса (РК), u ₂ – окружная скорость на выходе из РК) и КПД η. Предметом представляемой работы является характеристика коэффициента теоретического напора. Согласно [2], функция ^ T = f ( ф 2 ) (где ф 2 — коэффициент расхода на выходе из РК) линейная и не зависит от числа Маха, если режим течения дозвуковой. Экспериментальные данные, которыми располагают авторы, это подтверждают. Практически линейны размерные напорные характеристики многоступенчатых компрессоров, на что указывают данные заводских испытаний в работе [3].

Линейность напорной характеристики идеального РК с бесконечным числом лопаток легко объяснима [1]. Почему не нарушается линейность зависимости при конечном числе лопаток и большом влиянии вязкости (особенно на нерасчетных режимах, где существуют большие зоны отрыва потока), авторы не могут объяснить, что не мешает использовать это обстоятельство при анализе и расчете.

Напорная характеристика модельной ступени типа 028

Анализ линейной зависимости ^ т = f ( ф ₂ ) авторы приводят ниже на примере характеристик модельной ступени 028 семейства 20СЕ Проблемной лаборатории компрессоростроения СПбПУ [4]. Это ступень промежуточного типа в составе рабочего колеса с цилиндрическими лопатками, безлопаточного диффузора с шириной основного участка меньше высоты лопаток РК на выходе и обратно-направляющего аппарата. Схема проточной части в меридиональной плоскости с указанием основных размеров изображена на рис. 1.

В соответствии с принципами проектирования методом универсального моделирования [1, 5-8] лопаточная решетка оптимизировалась на основе анализа диаграмм скоростей невязкого потока (расчет по программе 3ДМ.023). На рис. 2 показана схема проточной части РК 028 и вид его лопаточной решетки.

На рис. 3 даны диаграммы меридиональных скоростей на восьми осесимметричных поверхностях тока и диаграммы скоростей на трех поверхностях тока по высоте лопаток. Условный коэффициент расхода соответствует маленькому отрицательному углу атаки на периферии лопаток. Этот режим рекомендован в качестве расчетного как режим минимального коэффициента сопротивления рабочего колеса [9].

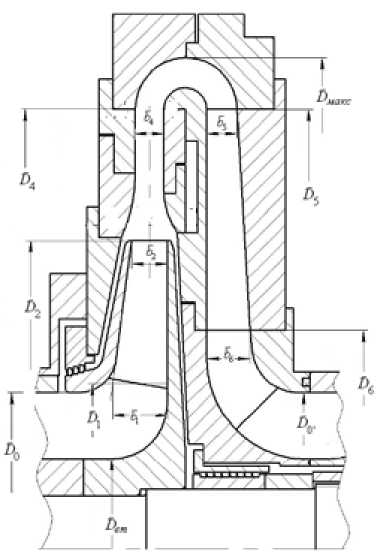
Рис. 1. Схема проточной части ступени промежуточного типа в меридиональной плоскости с названиями основных размеров

Fig. 1. Meridional scheme with main dimensions of the stage impeller+VLD+RCH

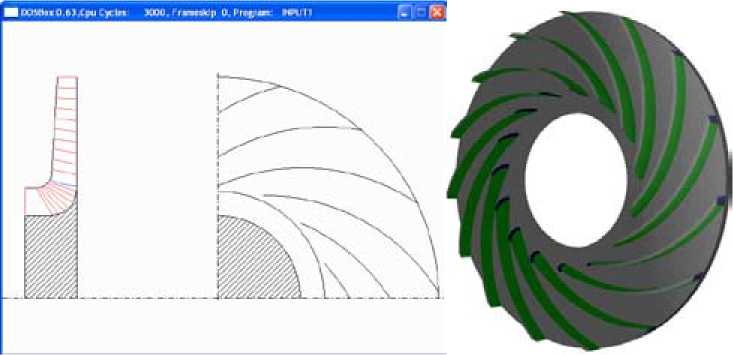
Рис. 2. Программа 3ДМ.023. Схема проточной части и вид лопаточной решетки РК типа 028

Fig. 2. The program 3DМ.023. Flow path scheme and the blade row of the impeller type 028

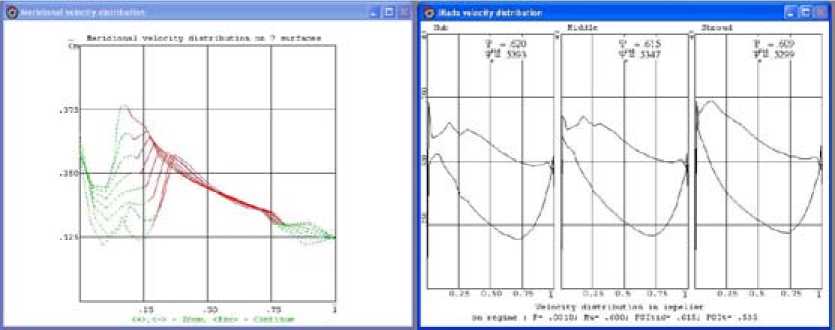
Рис. 3. Программа 3ДМ.023. Диаграммы меридиональных скоростей на восьми осесимметричных поверхностях тока (слева) и диаграммы скоростей на трех поверхностях тока по высоте лопаток (справа)

Fig. 3. The program 3DМ.023. Diagrams of the meridional velocity of eight quasi orthogonals (left) and velocity diagram on the hub, on the mean surface and on the shroud (right)

Рис. 4. Формы выходных кромок лопаток рабочего колеса [1]

Fig. 4. Shape of impeller trailing edge [1]

Ступень испытывалась при трех значениях условного числа Маха M_u = 0,60, 0,70, 0,80. При испытании ступени с двумя разными размерами обратно-направляющего аппарата напорные характеристики рабочего колеса совпали в пределах точности эксперимента.

В [1] рассмотрены варианты формы выходной кромки лопаток РК, влияющие на напорную характеристику (рис. 4).

Слева рекомендованное в [9] симметричное заострение. Вторая слева форма тупая. При соединении основного и покрывающего дисков сваркой такая форма получается после чистовой обточки РК по наружному диаметру. На основании опытов с модельными ступенями в [1] указано, что при этих двух формах напорные характеристики совпадают и есть слабая тенденция к росту КПД у РК с заостренной формой. Третья слева конфигурация с заострением со стороны задней поверхности соответствует классической рекомендации школы НЗЛ [10]. При этом фактический выходной угол лопатки β л 2 больше угла, отсчитываемого от средней линии. В [1] такое заострение или заострение со стороны передней поверхности (справа на рис. 3) рекомендовано для «подстройки» напорной характеристики РК с тупой кромкой при желании увеличить (заострение со стороны задней поверхности) или уменьшить напор (заострение со стороны передней поверхности).

Рабочее колесо 028 испытывалось с тупой выходной кромкой, с заострением кромки с передней стороны и с заострением кромки с передней стороны на половину толщины лопатки.

Всего проведено 15 испытаний. Результаты одного испытания, видимо, содержат случайную ошибку, так как напор на 2-3 % ниже, чем при других испытаниях этого варианта ступени. Это испытание исключено из рассмотрения.

На рис. 5 приведены результаты испытания ступени 028 с тупой выходной кромкой при M_u = 0,60. Характеристики представлены в обычном для модельных ступеней виде П , V i = f ( ^ ) , где Ф — условный коэффициент расхода; y i - коэффициент внутреннего напора. Красные точки и линии у ступени с постоянной высотой лопаток обратно направляющего аппарата (ОНА), серые и зеленые – два испытания ступени с ОНА с b 5 < b 6 , где b 5 – высота лопаток ОНА на входе, м; b₆ – высота лопаток ОНА на выходе, м. Штриховые линии – эксперимент, сплошные линии – моделирование (расчет) характеристик по 8-й версии метода универсального моделирования [10].

У вариантов с ОНА при соотношении высот лопаток b 5 < b 6 расчет КПД достаточно точен. Но математическая модель некорректно учитывает влияние отношения b₅ / b₆ на потери в ОНА при b 5 = b 6 . Предсказывается рост КПД, в то время как измеренный КПД при этом меньше. Правильно предсказано только смещение характеристики в сторону больших расходов. Моделирование характеристики КПД не предмет этой работы. Достаточно указать, что на моделирование напорной характеристики некорректность расчета КПД у варианта ступени 028 при b 5 = b 6 не оказывает влияния.

При построении характеристик ^ т = f (⁽ Р 2 ) экспериментальные данные обрабатывались следующим образом. Коэффициент внутреннего напора рассчитывался по измеренной величине повышения температуры торможения в РК:

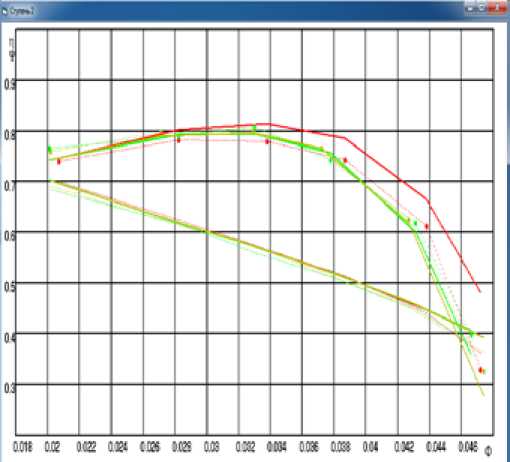
Рис. 5. Результаты трех испытаний ступени 028 с тупой выходной кромкой при M_u = 0,60 (монитор программы IDENT). Штриховые линии – эксперимент, сплошные линии – расчет

Fig. 5. The test results of the stage 028 with a blunt trailing edge. M_u = 0,60 (IDENT program monitor). Dashed lines – experiment, solid lines – calculation

Vi =

c A T * ^p u 2

где T ^* – полная температура, К; c_p – теплоемкость при постоянном давлении, Дж/(кг*К).

Коэффициент теоретического напора определялся по измеренной величине коэффициента внутреннего напора с учетом коэффициентов протечек и дискового трения:

_____Vi_____, 1 + Рпр + Ртр

где β_пр – коэффициент протечек в лабиринтном уплотнении; β_тр – коэффициент дискового трения.

В [3] показано, что для повышения точности моделирования характеристик РК следует учесть поток протечек в лабиринтном уплотнении покрывающего диска mпр , который движется в рабочем колесе дополнительно к расходу газа в проточной части m. Расчет коэффициента расхода сделан по уравнению неразрывности с учетом коэффициента протечек Рпр = -пр. Ко эффициент сжимаемости £2 = р2 / р0 (где р2 - плотность газа на выходе из РК, кг/м3; р0 - плотность газа по полным параметрам на входе в РК, кг/м3) рассчитан по 8-й версии программы метода универсального моделирования [11]:

. = ^ . ф.= »(1 + А,),

где Ф0 – условный коэффициент расхода с учетом протечек.

Расчет коэффициентов так называемых щелевых потерь сделан по эмпирическим формулам метода универсального моделирования:

в = K ---^---

тр трФ X VT X Re °-2’ где Reu – условное число Рейнольдса; Kтр – эмпирический коэффициент, определяющий величину трения.

KD5 пл впр прФ Ф х D1 ,                                                           (5)

где D ₁ – относительный диаметр начала лопаток РК; K D – отношение диаметра начала лопаток к диаметру входе в РК; В упл - относительный зазор в лабиринтном уплотнении; К пр - эмпирический коэффициент, определяющий величину протечек.

Зависимости y _T = f ( ф ₂ ) для 14 испытаний ступени типа 028 приведены на рис. 6.

Приводимые на рис. 6 экспериментальные точки аппроксимируются прямыми линиями, задаваемыми коэффициентом теоретического напора при нулевом расходе ψ_{T 0} и углом наклона по отношению к оси ординат β T . В скобках указаны значения эмпирических коэффициентов моделирования напорной характеристики в 4-й версии математической модели [1] K μ и X pst 0 :

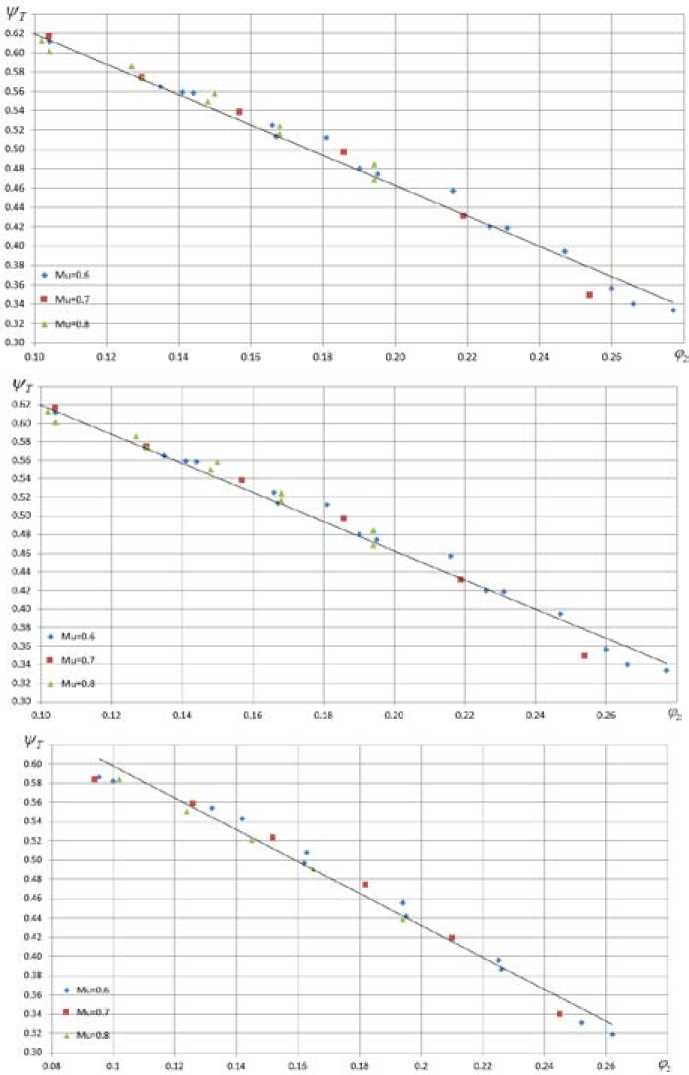
Рис. 6. Напорные характеристики РК типа 028 при M u = 0,60, 0,70, 0,80. Сверху – тупая выходная кромка лопаток, в центре – заострение на половину толщины со стороны передней поверхности, снизу – заострение со стороны передней поверхности

Fig. 6. The approximation of the loading factor characteristics of impeller type 028, M_u = 0,60, 0,70, 0,80. Above – blunt trailing edge, amidst – sharpening at half the thickness from the pressure side, below – sharpening from the pressure side

– тупая кромка ψ_{T 0} = 0,835, β_T = 29,7º ( K _μ = 1,75, X_{pst 0} = 2,40);

– заостренная на половину толщины со стороны передней поверхности ψ T 0 = 0,813, β T = 29,0º ( K μ = 2,20, X pst 0 = 2,20);

– заостренная со стороны передней поверхности ψ T 0 = 0,836, β T = 28,0º ( K μ = 2.20, X pst 0 = 2,0).

Линейные напорные характеристики, аппроксимирующие экспериментальные точки на 6

, использованы для сопоставления с рассчитанными разными способами характеристиками ступени типа 028. Они вместе представлены на рис. 7, невязкий расчет произведен для симметричной выходной кромки, также дана напорная характеристики для бесконечного числа лопаток. Пояснение по напорной характеристике при невязком течении сделано ниже.

При бесконечном числе лопаток угол наклона β_T равен углу лопаток β_{л 2}. Последний равен 30,3º у РК типа 028. Тот факт, что экспериментальные характеристики практически параллельны характеристике при бесконечном числе лопаток, не имеет, к сожалению, универсального характера. Иначе моделирование зависимости у _т = f ( ^ 2 ) было бы значительно проще. При больших выходных углах угол β_T значительно меньше выходного угла лопаток.

Обращает внимание не вполне закономерное влияние способа заострения на протекание характеристики. При полном заострении значение коэффициента напора при нулевом расходе практически такое же, как при тупой выходной кромке (ψ T 0 равно 0,835 и 0,836 соответственно). Но за счет меньшего угла наклона при полном заострении коэффициент напора в рабочем диапазоне меньше. При заострении на половину толщины можно ожидать промежуточное значение коэффициента напора в диапазоне рабочих режимов, а оно меньше, чем при полном

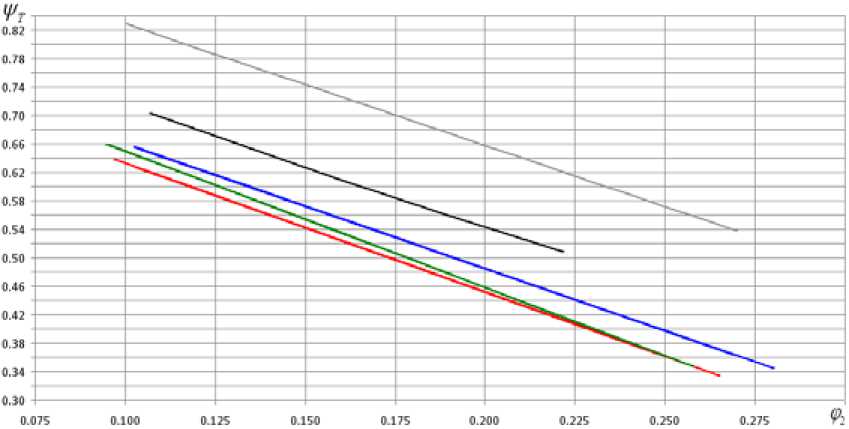
Рис. 7. Напорные характеристики РК типа 028. Синий – тупая выходная кромка лопаток, красный – заострение на половину толщины со стороны передней поверхности, зеленый – заострение со стороны передней поверхности, черный – невязкий поток, серый – бесконечное число лопаток

Fig. 7. The loading factor characteristics of impeller type 028. Blue – blunt trailing edge, red – sharpening at half the thickness from the pressure side, green – sharpening from the pressure side, black – inviscid flow, gray – infinite number of blades

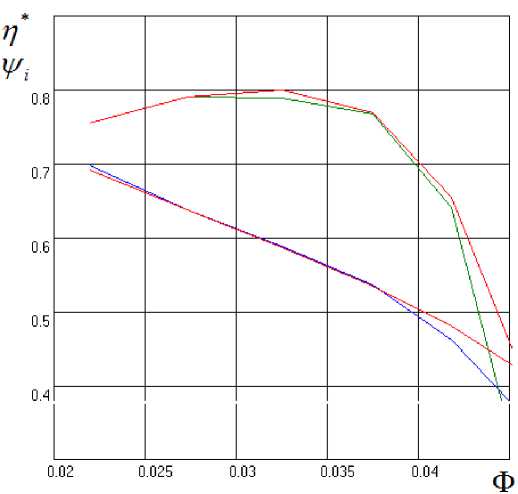
Рис. 8. Характеристики ступени 028 с тупой выходной кромкой при M_u = 0,70 (монитор программы IDENT). Зеленые линии – эксперимент, красные линии – расчет по математической модели

Fig. 8. The characteristics of the stage 028 with blunt trailing edge, Mu = 0,70 (IDENT program monitor). Green – experiment, red – calculation заострении, из-за меньшего значения ψT0 = 0,813. Угол наклона стал больше и практически равен углу при тупых выходных кромках.

На рис. 8 показаны характеристики ступени 028 с тупой выходной кромкой при M u = 0,70 и смоделированные по 8-й версии математической модели характеристики.

Диапазон Ф = 0,020 – 0,040 характерен для рабочих режимов ступени в составе компрессора. Моделирование в этом диапазоне достаточно точное. Информация о параметрах потока в трех точках характеристики представлена в табл. 1.

В столбце 1 даны значения коэффициента расхода, при которых производилось измерение параметров ступени. В столбцах 2, 4, 5 отражены значения параметров, рассчитываемыt по математической модели на основании результатов испытания. В столбце 6 и 7 представлены

Таблица 1. Параметры ступени типа 028 и ее напорной характеристики при M u = 0,70

Table 1. Parameters of stage 028 and its loading factor characteristics, M_u = 0,70

1 2 3 4 5 6 7 8 9 10 11 Ф βпр Ф0 φ20 тр ψi ψT η* n ψT ид ψT ψT ид 0,0375 0,0151 0,0381 0,188 0,0316 0,537 0,513 0,768 1,592 0,561 0,914 0,0325 0,0174 0,0331 0,160 0,0338 0,588 0,559 0,800 1,556 0,609 0,918 0,0219 0,0258 0,0225 0,107 0,0432 0,653 0.647 0,755 1,609 0,703 0,920 коэффициент внутреннего напора и политропный КПД по полным параметрам, рассчитанные по измеренным параметрам потока.

При коэффициентах расхода в столбце 3 рассчитан невязкий квазитрехмерный поток в РК типа 028 при Mu = 0,70. Расчеты проведены при показателе политропы в столбце 9, рассчитан-n*k ные исходя из соотношения ≈η     , где k – показатель изоэнтропы. Здесь использование n-1     k-1

КПД ступени по полным параметрам делает соотношение приближенным, но более точный расчет по статическому КПД колеса (также рассчитывается по математической модели, но не выводится на дисплей) дает незначительное уточнение. Значение φ 20 , определяющее величину коэффициента расхода на выходе из РК с учетом протечек, которое рассчитывает программа невязкого течения при учете КПД, незначительно отличается от расчета по математической модели.

Рассчитанные по программе 3ДМ.023 значения коэффициента напора невязкого потока показаны в столбце 10, а отношение экспериментального и невязкого коэффициентов напора – в столбце 11. Расчет коэффициента теоретического напора программа 3ДМ.023 делается на основании постулата Жуковского-Чаплыгина о том, что критическая точка находится на острие выходной кромки. Применительно к центробежным рабочим колесам с лопатками постоянной толщины это означает, что критическая точка расположена на пересечении средней лини профиля с диаметром рабочего колеса. Лопатки предполагаются симметрично заостренными (рис. 4 слева). Испытанное колесо имело тупые выходные кромки, но эксперименты не выявили влияния этого различия формы на напорную характеристику.

По очевидному уравнению прямой линии значения в столбцах 4 и 10 дают угол наклона напорной характеристики невязкого потока, который оказался равным β_{T ид} = 29,7º, а коэффициент теоретического напора ψ T0 ид = 0,892. Это точно совпадает с углом наклона испытанного РК с тупой выходной кромкой. При бесконечном числе лопаток угол наклона равен выходному углу лопаток (30,3º у РК типа 028).

При бесконечном числе лопаток коэффициент напора при нулевом расходе равен единице. У рабочего колеса типа 028 при движении невязкого газа этот коэффициент напора равен 0,891, т.е. из-за конечного количества лопаток коэффициент меньше на 10,9 %. У реального РК типа 028 этот коэффициент равен 0,835. То есть из-за вязкости коэффициент напора при нулевом расходе уменьшается еще на 5,6 %. Линейные характеристики при невязком течении и при бесконечном числе лопаток показаны на рис. 8.

Для проверки возможностей моделирования напорной характеристики ступени типа 028 CDF-методами сделан ряд расчетов по программе NUMECA Fine Turbo при следующих условиях (так же рассчитаны характеристики других РК, приводимые ниже):

– на входе в расчетную область задавались полное давление и полная температура;

– на выходе задавался массовый расход.

Расчеты производились для одного межлопаточного канала без учета протечек через лабиринтные уплотнения. Пробные расчеты показали, что при расчете всей лопаточной решетки получается идентичная напорная характеристика. Применяли модель турбулентности – 1051 –

Спалларта-Алмарраса. Число ячеек сетки выбирали согласно рекомендациям, сделанным в [11].

Коэффициент расхода по программе NUMECA Fine Turbo рассчитывали двумя способами. Из уравнения неразрывности:

ρ ₂ π D ₂ b ₂ u ₂

где D 2 – наружный диаметр РК, м; b 2 – высота лопатки РК на выходе, м.

Второй способ – из расчета кинематики потока с осреднением скорости на выходе из РК (обозначения из инструкции пользователя программы НУМЕКА):

Z q • |ds| q = Z

s где q – осредняемая величина; S – площадь поверхности, м2.

Формула (7) не учитывает изменение плотности ρ 2 по поверхности сечения на выходе из РК, но пробный расчет показал пренебрежимо малое уточнение на 0,1 % при учете плотности.

Коэффициент напора также рассчитывался двумя способами. Первый – по формуле (1). Так как щелевые потери не моделировались, по формуле (1) программа NUMECA рассчитывает коэффициент не внутреннего, а теоретического напора.

Второй способ – из расчета кинематики потока определялось значение c_{u 2}. Использован способ осреднения скорости на выходе из РК по формуле (7). Это не вполне строгое осреднение. Более строгое осреднение по массовому расходу

Z cu2 " cr2 " P2 " Ids |

s

^CU2 Z Cr2 • P 2 • ^S| ,

s где cr2 – радиальная составляющая абсолютной скорости, м/с.

На рис. 9 сопоставлены значения коэффициента расхода на выходе из рабочего колеса в зависимости от условного коэффициента расхода.

Красная линия – обработка экспериментальных характеристик по математической модели, достаточно точно описывающей результаты эксперимента. Зеленая линия – расчет NUMECA из уравнения неразрывности по формуле (6). Черная линия расчет NUMECA с осреднением скорости на выходе из РК по формуле (7). Оба расчета по NUMECA дают близкие результаты. Небольшое отличие от экспериментальных данных должно оказывать влияние на напорную характеристику. В расчетной точке Ф 0 ≈0,0325 это отличие менее 2 % – коэффициент расхода по NUMECA меньше. Это дает превышение рассчитанного коэффициента напора на 1,5 %.

На рис. 10 и 11 сопоставлена измеренная зависимость ψ T = f ( φ 2 ) с напорными характеристиками, рассчитанными разными способами. На рис. 10 φ ₂₀ рассчитан по ф. (6), ψ_T – по ф. (1). На рис. 11 φ 20 и ψ T рассчитаны по осредненным значениям скоростей по ф. (7).

От минимального коэффициента расхода до φ ₂₀ = 0,180 рассчитанные характеристики при разных Махах совпадают, но зависимость ψ T = f ( φ 2 ) не вполне линейная. При больших расходах – 1052 –

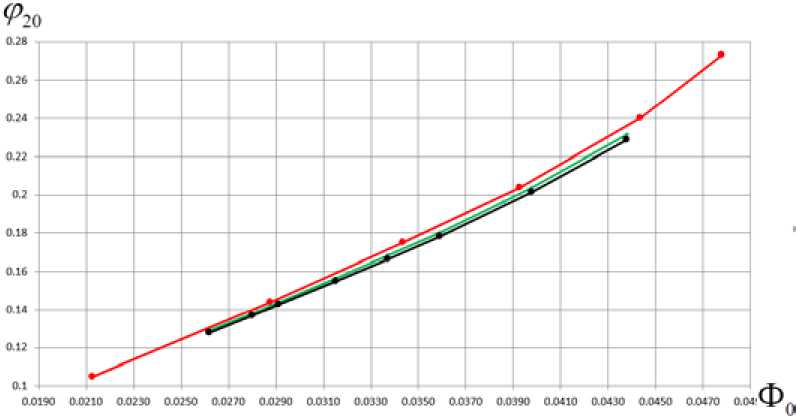
Рис. 9. Коэффициент расхода на выходе из РК в зависимости от условного коэффициента расхода. Красный – эксперимент с перерасчетом по ф. (3), зеленый – расчет NUMECA по ф. (6), черный – расчет NUMECA по ф. (7)

Fig. 9. The flow rate coefficient at the impeller exit versus flow rate coefficient Ф. Red – experiment with recalculation at f. (3), green – NUMECA calculation in f. (6), black – NUMECA calculation at f. (7)

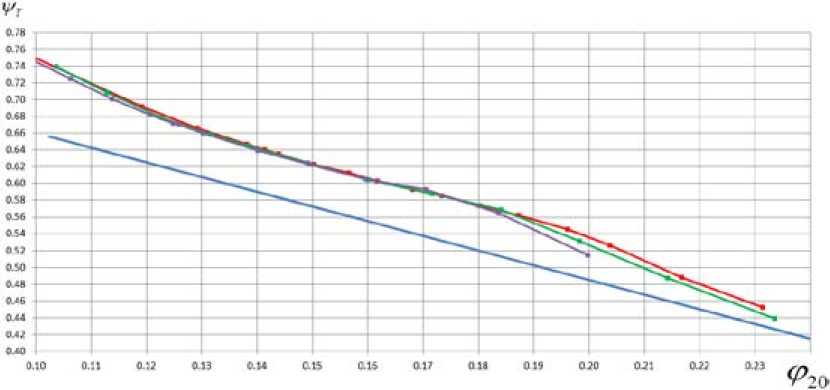
Рис. 10. Сравнение аппроксимированной экспериментальной напорной характеристики (синий) ψ T = f ( φ 2 ) рабочего колеса 028 с расчетом по программе NUMECA φ 20 по ф. (6), ψ T по ф. (1). Красный – M u = 0,6, зеленый – M u = 0,7, фиолетовый – M u = 0,8

Fig. 10. Comparison of the experimental and approximated loading factor characteristics (blue) ψ_T = f ( φ ₂) of the impeller 028 with calculation by program NUMECA. φ ₂₀ calculated by formula (6), ψ_T by formula (1). Red – M_u = 0,6, green – M_u = 0,7, purple – M_u = 0,8

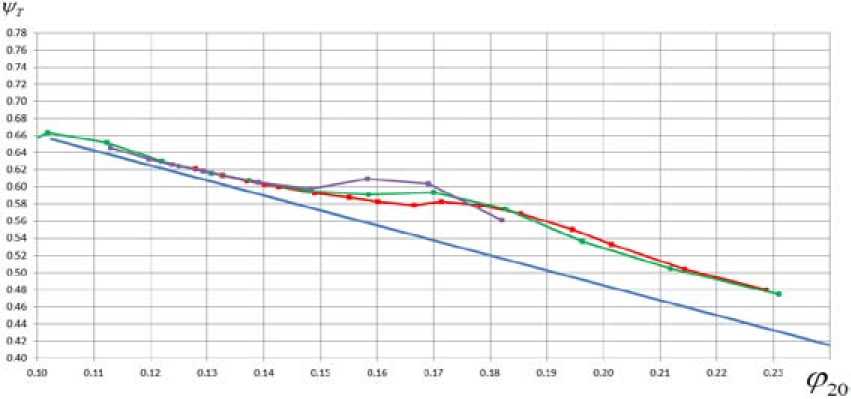
Рис. 11. Сравнение аппроксимированной экспериментальной напорной характеристики (синий) ψ T = f ( φ 2 ) рабочего колеса 028 с расчетом по программе NUMECA φ 20 и ψ T рассчитаны по осредненным значениям скоростей по ф. (7). Красный – M u = 0,6, зеленый – M u = 0,7, фиолетовый – M u = 0,8

Fig. 11. Comparison of the experimental and approximated loading factor characteristics (blue) ψ_T = f ( φ ₂) of the impeller 028 with calculation by program NUMECA. φ ₂₀ and ψ_T calculated by averaged values of velocity by formula (7). Red – M_u = 0,6, green – M_u = 0,7, purple – M_u = 0,8

характеристики при разных Махах расходятся и уменьшают угол наклона. По формулам (6) и (1) превышение рассчитанного коэффициента напора вблизи расчетного режима с φ 20 ≈ 0,15 порядка 8,8 %.

Влево от расчетного режима рассчитанная по осредненным скоростям c r 2 и c u 2 на рис. 11 характеристика приближается к экспериментальной характеристике. Это можно было бы считать хорошим результатом, но отличия от коэффициентов напора на рис. 10 не может быть в реальном процессе сжатия. При φ ₂ >  φ _{2 расч} функция ψ_T = f ( φ ₂) принимает незакономерный характер. Происходящее трудно объяснить, поскольку та же функция, рассчитанная по формулам (1) и (6), достаточно закономерна.

На рис. 12 показано поле скоростей в рабочем колесе на расчетном расходе и на расходе больше расчетного, где происходит незакономерное увеличение коэффициента напора на рис. 11.

При φ ₂ >  φ _{2 расч} у входной кромки на передней поверхности виден отрыв потока, распространяющийся вглубь канала. По данным измерений и визуализации отрывы на передней поверхности не возникают [1, 9], в рассчитанной модели течения отрыв может повлиять на структуру потока в выходном сечении РК, где осредняются скорости c r 2 и c u 2 .

На рис. 13 излображено поле скоростей c_{r 2} на выходе из РК на трех режимах по расходу (один межлопаточный канал).

Неравномерность поля c_{r 2} увеличивается с ростом расхода. Но на рис. 9 осредненные значения c r 2 не отличаются от рассчитанных значений из уравнения неразрывности. Значит, появление области незакономерно протекающей характеристики не связано с осредненным значением c r 2 .

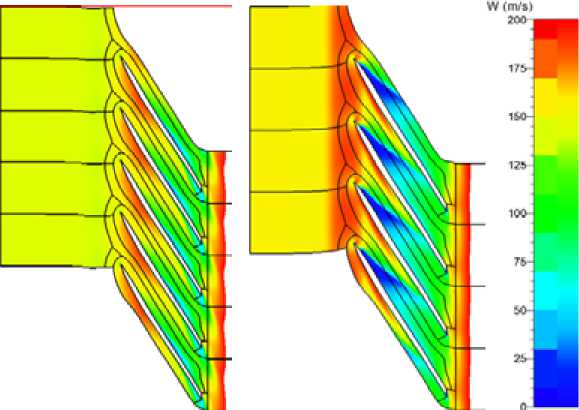
Рис. 12. Поле скоростей в рабочем колесе типа 028 на расчетном расходе и на расходе больше расчетного. Периферийная осесимметричная поверхность тока (ОПТ), M_u = 0,80. Слева φ ₂₀ = 0,1482, справа φ 20 = 0,1582

Fig. 12. The velocity field in the impeller type 028 on the design flow rate and on the higher flow rate. Peripheral axisymmetric surface current, M_u = 0,80. Left φ ₂₀ = 0,1482, right φ ₂₀ = 0,1582

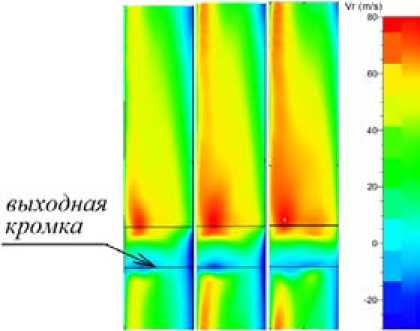
Рис. 13. Поле скоростей c r 2 на выходе из РК типа 028 на трех режимах по расходу. Слева Ф = 0,1249, в центре Ф = 0,1482, справа Ф = 0,1582. M u = 0,80

Fig. 13. The c_{r 2} velocity field at the outlet of the impeller type 028 at three flow rates. Left Ф = 0,1249, amidst Ф = 0,1482, right Ф = 0,1582. M u = 0,80

На рис. 14 показано поле скоростей c_{u 2} на выходе из РК на трех режимах по расходу (один межлопаточный канал).

На размере зоны повышенных значений c_{u 2} режим работы сказывается мало. Авторы не имеют объяснения несоответствия значений коэффициента теоретического напора, рассчитанного по программе NUMECA двумя способами (рис. 10 и 11). Непонятно возникновение зоны незакономерного протекания характеристики.

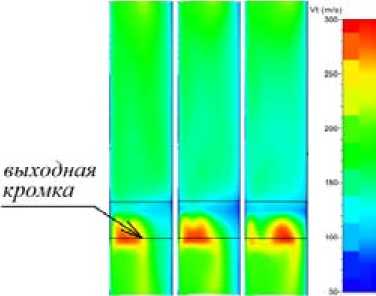
Рис. 14. Поле скоростей c_{r 2} на выходе из РК типа 028 на трех режимах по расходу. Слева Ф = 0,1249, в центре Ф = 0,1482, справа Ф = 0,1582. M_u = 0,80

Fig. 14. Tangential velocity field at the outlet of the impeller type 028 at three flow rates. Left Ф = 0,1249, amidst Ф = 0,1482, right Ф = 0,1582. M u = 0,80

Напорные характеристики ряда модельных ступеней

Для дальнейшего анализа на других объектах по аналогичной методике были рассчитаны напорные характеристики серии из 10 модельных ступеней промежуточного типа со значениями коэффициентов расхода в диапазоне Ф расч = 0,15 – 0,015 при M u = 0,55. Схема ступеней аналогична схеме, показанной на рис. 1, но все рабочие колеса осерадиальные. Результаты CFD-расчетов сопоставлены с расчетными параметрами ступеней. Графики, подобные графикам на рис. 10 и 11, заняли бы слишком много места. Ниже представлена базовая информация.

На рис. 15 в зависимости от Ф _расч отражены отношения коэффициентов напора по формулам (1) и (7) к расчетному коэффициенту напора ψ T расч = 0,50, одинаковому для всех ступеней с Ф _расч = 0,15 – 0,015. Зелеными точками на рис. 15 и 16 показаны значения ψ _T / ψ_{T расч} и φ ₂₀ / φ _{20 расч} для РК типа 028. Отличием рассчитанных по математической модели и по программе NUMECA коэффициентов напора в пределах 2-4 % нельзя пренебречь.

На рис. 16 для РК с разными Ф расч представлены отношения коэффициентов расхода по формулам (7) и (8) к коэффициенту расхода φ _{20 расч} по проекту.

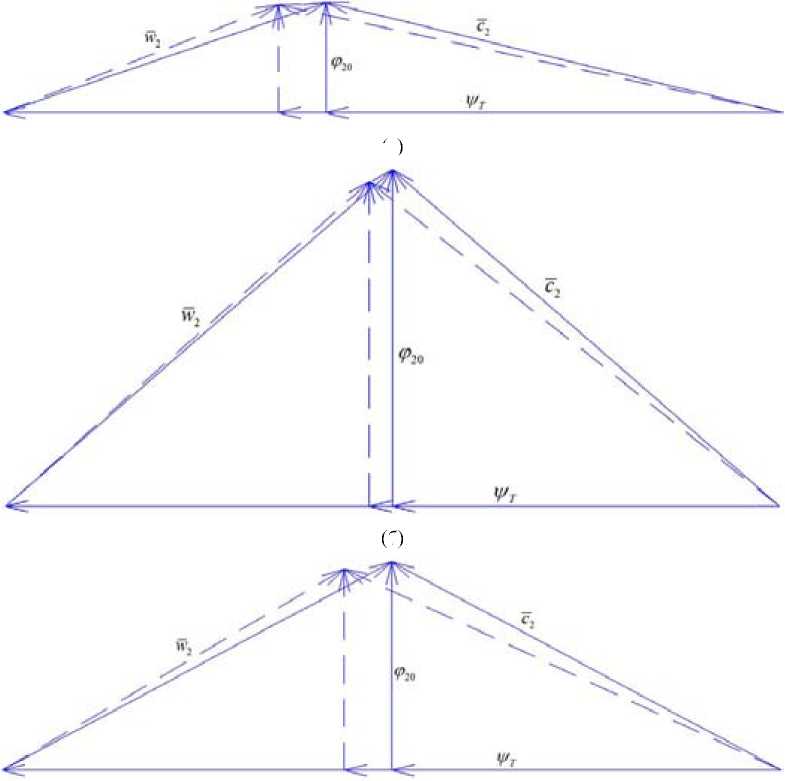
На рис. 17 изображены треугольники скоростей на расчетном режиме для ступени 028 и модельных ступеней с Ф _расч = 015, 0,065 и 0,015 по проектным значениям φ _{20 расч} и ψ_{T расч} . На них наложены треугольники скоростей по результатам CFD-расчета с ψ T по формуле (1) и с φ 20 по формуле (6).

На рис. 18 приведены данные по наклону напорной характеристики по математической модели и по СFD-расчету в зависимости от Ф _расч .

Приведенные данные демонстрируют все еще непреодоленные сложности корректного расчета газодинамических характеристик центробежных ступеней CFD-методами. Особенно показательно несовпадение коэффициентов теоретического напора, рассчитанных по параметрам потока двумя разными способами. Уравнение энергии в потоке газа c p ( T 2* - T 0* ) = h_T + Q _bh (где h T – теоретический напор, Дж/кг; Q вн – количество теплоты внешнего теплообмена, Дж/кг) и – 1056 –

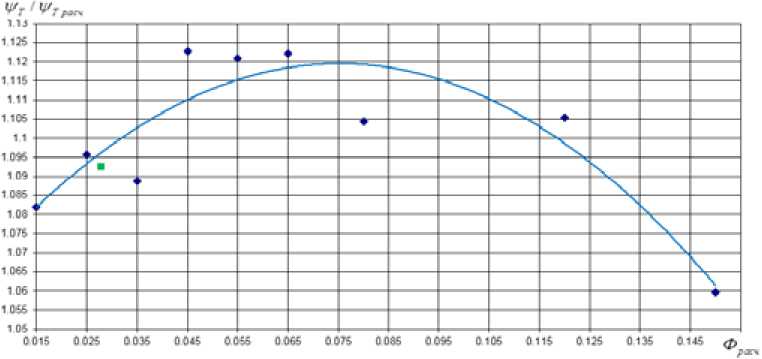
Рис. 15. Отношения коэффициентов напора по формулам (1) к расчетному коэффициенту напора

Fig. 15. Ratio of loading factor by the formula (1) to design loading factor

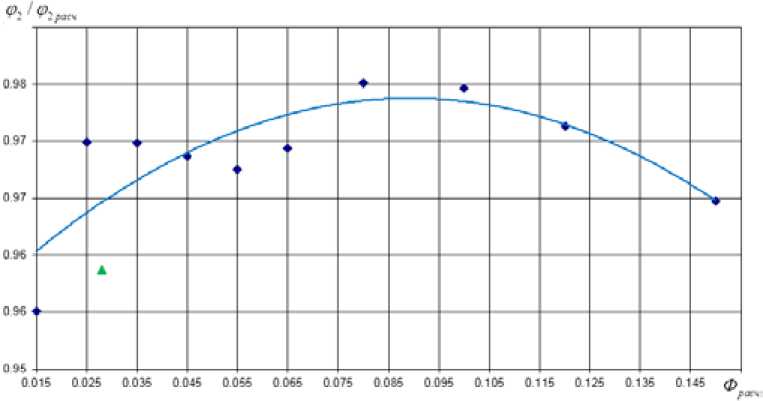
Рис. 16. Отношения коэффициентов расхода по формуле (6) (синий) к коэффициенту расхода φ 20 расч

Fig. 16. Ratio of flow rate coefficient by the formula (6) (blue) to flow rate coefficient φ _{20 расч}

основное уравнение турбомашин h_T = c_u2 х u₂ в реальности должны давать тождественные значения, указывают на невозможность неравенства h_T в реальном рабочем процессе. При расчетах

C p ( T - T * ) = c

u2u2

внешний теплообмен Q_вн принимается равным нулю, поэтому равенство у _T должно соблюдаться.

Возможность надежного расчета параметров потока и газодинамических характеристик центробежных компрессоров CFD-методами имеет большое значение для исследовательской и проектной практики. Исследования, направленные на повышение надежности расчетов центробежных компрессоров CFD-методами, следует продолжить.

(б)

(а)

Рис. 17. Треугольники скоростей на расчетном режиме для ступени 028 (а) и модельных ступеней с Ф расч = 0,15 (б), 0,065 (в) и 0,015 (г). Сплошная линия – расчет по математической модели, пунктирная линия – CFD-расчет по формулам (1) и (6)

Fig. 17. The velocity triangles on design flow rate on stage 028 (a) and model stages with Ф _расч = 0,15 (б), 0,065 (в) и 0,015 (г). Solid line – calculation on the mat. Model, dashed line – CFD-calculation by formulas (1) and (6)

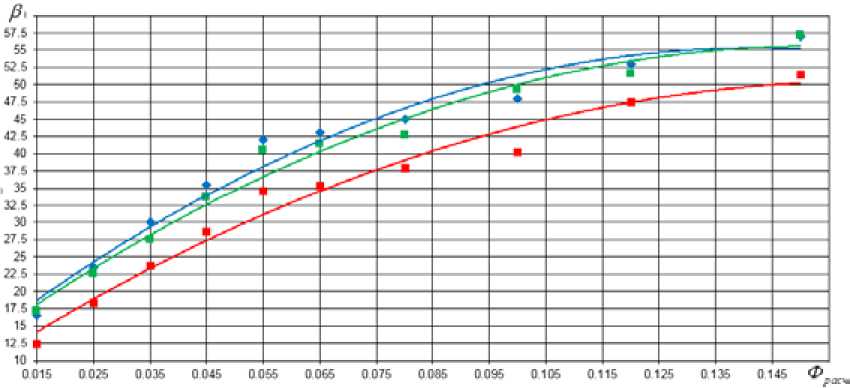
Рис. 18. Угол наклона напорной характеристики и выходной угол лопаток для ступеней с разными Ф расч . Красный – β T по результатам CFD-расчетов, ф (3) и (6), зеленый – β T по результатам расчетов по ММ, синий – выходной угол лопатки β л 2

Fig. 18. The inclination angle of loading factor characteristics and the output angle of the blades for stages with different Ф _расч . Red – β_T according to the results of CFD-calculations, formulas (3) and (6); green – β_T the results of the calculations for math. model, blue – output blade angle β_{л 2}

Выводы

Итак, перечислим основные положения данной статьи:

• –    подтвержден линейный характер напорной характеристики «коэффициент теоретического напора – коэффициент расхода»;

• –    установлено влияние формы выходной кромки на величину коэффициента напора при нулевом расходе и на наклон напорной характеристики по отношению к оси ординат;

• –    характеристики, рассчитанные CFD-методом, дают завышение коэффициента напора в расчетной точке до 8 %;

• –    рассчитанная напорная характеристика по уравнению неразрывности и повышению температуры торможения носит закономерный характер. Характеристика, рассчитанная по компонентам скорости на выходе из рабочего колеса, носит необъяснимый характер;

• –    изучение возможности применения CFD-методов для моделирования характеристик центробежных компрессорных ступеней следует продолжить.

Благодарность

Результаты, указанные в публикации, получены в результате выполнения Головным исполнителем научно-исследовательской, опытно-конструкторской технологической работы «Создание современного высокотехнологичного производства по проектированию, изготовлению и испытаниям установок, компримирующих газообразные продукты для эффективного использования в транспортных системах и технологиях». (При финансовой поддержке Правительства Российской Федерации (Минобрнауки России) – договор 02.G25.31.0140 от 01.12.2015 г.).