Анализ напряженного состояния диска компрессора ГТД

Фрактографические исследования поверхностей разрушения элементов конструкций авиационных газотурбинных двигателей (ГТД) показывают [1], что зарождение усталостных трещин часто происходит в окрестности ребер контактных поверхностей диска компрессора и лопаток. Определение очага зарождения и ориентации усталостных трещин необходимо для исследования их развития в процессе многоцикловой эксплуатации. В данной работе построена полная конечноэлементная модель [2] диска с лопатками и иными реальными элементами конструкции (удерживающие штифты, бандажные полки) и модель сектора диска с одиночной лопаткой. Расчетная схема включает комбинацию внешних нагрузок с учетом центробежных сил, распределенных аэродинамических давлений на лопатки [3] и нелинейного контактного взаимодействия диска, лопаток и иных дополнительных элементов конструкции. Результаты расчетов на полной модели использовались при построении более точного решения на подробной сетке со сгущением для сектора с одиночной лопаткой.

Разрушения в ободной части дисков компрессоров из титановых сплавов могут приводить к образованию фрагментов, которые либо остаются в двигателе, либо выходят за его пределы. Во всех случаях трещины возникают в скруглениях малого радиуса соединения «ласточ-

• * Данная работа выполнена в рамках реализации ФЦП «Научные и научнопедагогические кадры инновационной России» на 2009-2013 годы и гранта НШ-3288.2010.1.

кин хвост» (межпазовый выступ, рис. 1) и далее могут распространяться в двух направлениях: 1) вдоль радиуса диска, а далее, не доходя до ступичной части диска, возвращаются к ободу или останавливаются в отверстии в полотне диска; 2) развитие происходит по основанию межпазового выступа.

Рис. 1. Фотографии трещин в дисках компрессора

Описанные особенности зарождения трещины вдоль границы паза под лопатку указывают на существенную роль в разрушении диска на начальном этапе нагрузок, которые вызывались контактным воздействием лопатки. Определение очагов зарождения усталостных трещин в дисках и лопатках требует подробного описания полей напряжений и зон их концентрации. Расчетная модель, соответствующая циклу нагружения, должна учитывать два основных фактора нагружения: центробежную силу, соответствующую максимальной частоте вращения диска компрессора, аэродинамические нагрузки на лопатки, соответствующие максимальной (крейсерской) скорости полета, а также нагрузки контактного взаимодействия диска и лопаток.

Напряженно-деформированное состояние системы диск-лопатка определяется системой уравнений для тензора напряжений о и вектора скоростей v (или перемещений u , v = d t u ) во вращающейся с угловой скоростью ф системе координат

Vo + p®2r = рdtv dtо = X(ee: I)I + 2pee e = ee + ep, где область решения имеет вид Vt = {(x, t): x e V, t > 0}, t - время, x -лагранжев радиус-вектор, начало координат помещено на оси вращения, a - единичный вектор оси вращения, r = x - (x • a)a - вектор нормали, опущенной из точки с радиус-вектором x на ось вращения, dt - оператор лагранжевой производной по времени, e = (Vv + VvT) / 2 - тензор скоростей деформации, e e и e p - тензоры скоростей упругой и неупругой деформации.

Для базовой модели идеальной упругопластичности с условием пластичности Мизеса тензор скоростей неупругой (пластической) деформации исключается из приведенных выше уравнений с помощью соотношений закона пластического течения:

e ^p = A s s = о - ( о : I ) I / 3 Л >  0: s : s = 2 т 0 Л = 0: s : s <  2 т 0 .

Основными искомыми функциями являются перемещения, скорости и напряжения. Начальные условия имеют вид t = 0: u = 0, v = 0, о = 0.

На границе ( S = S _а u S u и S c ) задаются либо силовые граничные условия (участки S _а ), либо кинематические граничные условия (участки S u ), либо контактные условия (участки S c ).

Силовые граничные условия имеют вид x е Sа : Pn = Pn*(x, t) Pта = PтаД t) ( а = 1,2X где pn = n • о • n и pта = (о • п)та (а = 1,2) - нормальная и касательные составляющие поверхностной нагрузки, выраженные через тензор напряжений, n и та (а = 1,2) - векторы нормали и касательных к граничной поверхности. При аэродинамических нагрузках считается, что касательные нагрузки отсутствуют, pта = 0, а нормальная pn = p* (x, t) обусловлена аэродинамическим давлением.

Кинематические граничные условия на Su имеют вид x е Su:     u = u*(x,t), где u* = u*(x, t) - заданная функция координат и времени.

В простейшем случае контактные условия задавались в предположении идеального контакта (полного сцепления):

[ un ]=[ u т] = [ pn ]=[ p т] , при котором смещения и поверхностные напряжения непрерывны. Здесь квадратные скобки использованы для обозначения скачков.

В общем случае контактные условия допускают проскальзывание с трением и отлипанием, а зона контакта (участки границы с нулевым скачком нормальных перемещений) является переменной во времени. В зоне контакта условия имеют вид

[ u„ ] = 0, [ v т ] = 0: p„ <0, | p J^ q\P n\

[ u n ] = 0, [ v t ] * ⁰ : P n <  ⁰, P т ⁼ q|P n | [ v t ]/|[ v t ]| .

В зоне отлипания контактные условия имеют вид

[ un ]> 0 : P т = Pn = 0

При q = 0 имеем контакт с отлипанием и проскальзыванием без трения.

Для определения распределенных аэродинамических нагрузок на лопатки принимается гипотеза изолированного профиля [4]. Обозначим: го - частота вращения диска, x - локальная продольная координата хорды сечения, Р - угол между радиальной составляющей скорости и результирующим вектором скорости, w = ^v22 + го2r2 - модуль результирующей скорости, у(r) - переменная крутка сечения, где r -радиальная координата сечения. Локальный угол атаки сечения v а = у(r) - arctg —. Локальный шаг решетки t = 2 лr / N, где N - число го r лопаток на диске. Формулы для перепада давлений в случае одной обтекаемой пластины и в случае обтекания решетки пластин, полученные с использованием методов ТФКП [5], имеют следующий вид:

распределение давлений по поверхности одиночной лопатки

A p ( r , x ) = р ( v ² + го ² r ² )     a ^ sin2 1 у ( r ) - arctg— I ,

a + x + 5 V           го r J

распределение давлений по поверхности лопатки в решетке

_- aN

A p ( r , x ) = р ( v 2 2 + го ² r ² ) e ^{2 r}

, N ( a - x )

sh

——2 r —— sin 2 у ( r ) - arctg — .

N ( a + x + 5 )      V            _{го r} J

2 r

Точные решения из-за острой передней кромки содержат особенность при x = - а , для снятия этой особенности в формулы введен малый радиус скругления передней кромки 5 .

Сжимаемость газа можно учесть введением множителя Прандт-ля-Глауэрта 1/V1 - M2, где M = w / c = Jv22 + го2r2 / c - число Маха набегающего потока, p ± (r, x) = p ± (r, x )Ы1 - M2, Apc (r, x) = = Ap(r, x) / V1 - M2, c - скорость звука. Данное рассмотрение справедливо при выполнении условия дозвукового обтекания ^v^ + со2r2 < c для любого сечения лопатки. Полученные распределения давлений по поверхности лопатки можно использовать в качестве внешних нагрузок для расчета напряженно-деформированного состояния контактной системы диск-лопатка ГТД.

Для исследования выбран диск с лопатками компрессора двигателей серии Д30. Для этого объекта имеется наибольшее количество данных о происшествиях, дефектах и случаях разрушения, а также фрагментов, изученных методом фрактографии поверхностей излома, зон зарождения усталостных трещин, накопления усталостных бороздок и т.п.

Анализ напряженно-деформированного состояния контактной системы диск-лопатка ГТД с учетом дополнительных элементов конструкции требует создания полной геометрической и расчетной модели. Результат этого построения с использованием программного комплекса [2] представлен на рис. 2 и 3. Геометрическая полная модель с конечно-элементным разбиением приведена на рис. 4.

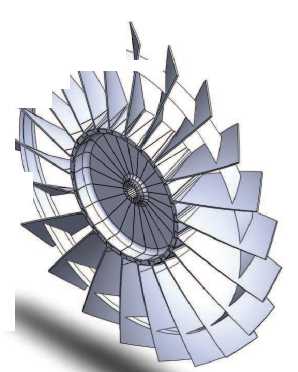
Рис. 3. Модель с бандажом

Рис. 4. Сетка

Рис. 2. Модель без бандажа ' ' " '

В представленных ранее [3] решениях задач о вращении диска компрессора со свободной лопастью лопатки (см. рис. 2) были получены высокие уровни перемещений конца лопатки, вызванные изгибом лопасти в результате внешних воздействий. Реальная конструкция снабжена так называемой бандажной полкой (см. рис. 3), которая должна препятствовать свободному изгибу лопастей, повышая жесткость конструкции.

Численное решение полномасштабной задачи не может быть получено с использованием современного персонального компьютера по следующим причинам. Расчетная модель сектора диска с одной лопаткой требует для удовлетворительного разрешения области концентрации напряжений (основание лопатки и крепежный вырез) создания расчетной сетки, содержащей до 100000 элементов. Время решения такой задачи, в основном за счет обработки контактных условий, составляет от 1 до 1,5 часов.

Таким образом, аналогичная сетка для полномасштабной задачи будет содержать 2 - 10 6 ^ 3 - 10 6 элементов. С учетом нелинейной зависимости времени вычислений от количества элементов решение вряд ли будет получено в обозримые сроки. Кроме того, объем оперативной памяти, необходимый для обработки такой задачи существенно превышает возможности персональных компьютеров. С учетом сказанного был реализован вариант решения задачи для отдельного сектора диска с одной лопаткой (рис. 5).

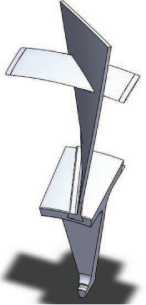
Рис. 5. Отдельный сектор диска с одной лопаткой

Рис. 6. Фрагмент сетки с лопаткой полной модели

В расчете отдельного углового сектора возникает проблема постановки граничных условий на левой и правой плоскостях, вырезающих этот угловой сектор. Корректная постановка задачи для отдельного сектора должна содержать фактические перемещения бандажной полки в качестве граничных условий на отсекающих сектор поверхностях. Эти перемещения могут быть получены только из решения полномасштабной задачи. Поскольку решение такой задачи на качественной сетке с учетом контактных условий пока технически невозможно, расчет был выполнен на сетке без существенного сгущения и при условиях полного сцепления контактных поверхностей. Фрагмент сетки изображен на рис. 6.

Приведем результаты сопоставления решения с учетом бандажной полки с решением без учета бандажной полки. Предполагается, что диск компрессора ГТД, оснащенный лопатками, вращается в набегающем потоке с угловой скоростью го = 300 рад/с (2865 об/мин). Скоростной напор на бесконечности Уг р- V ² = 20000 н, что соответствует скорости потока 200 м/с при плотности 1 кг/м ³ . На рис. 7 и 8 представлены уровни перемещения на деформированной форме модели (для наглядности перемещения увеличены в 5 раз). Видно, что бандажная полка существенно препятствует изгибу лопаток.

Рис. 7. Перемещения модели без полки

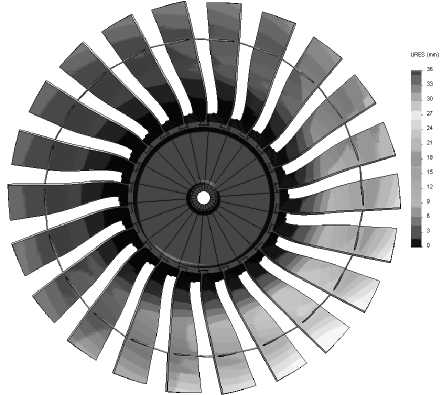
Рис. 8. Перемещения модели с полкой

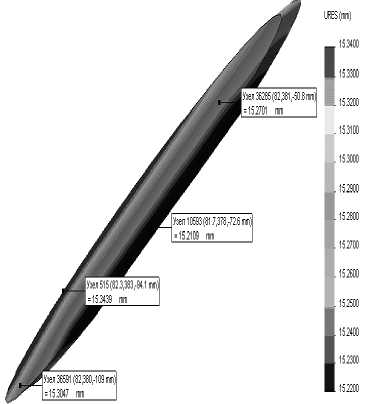
Рис. 9. Перемещения в сечении лопатки

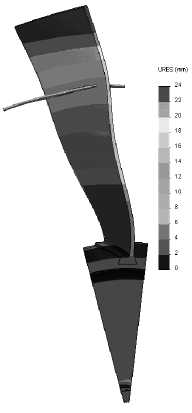
Рис. 10. Перемещения в секторе

Найдем перемещения бандажной полки в сечениях, соответствующих торцам отдельного сектора. Поскольку перемещения почти однородны по сечениям (рис. 9), искомые значения можно определить из их распределений вдоль круговой кромки бандажной полки.

Обозначим u r , u 0 и u z проекции перемещений в цилиндрической системе координат, связанной с осью вращения. Граничные перемещения u r 1 « u r2 « 0,4 мм, u e i ® и _{0 2} « 15,2 мм, u z 1 « u z ₂ « 5 мм. Здесь индексы 1 и 2 выделяют перемещения, соответствующие левому и правому торцу. Граничные условия на левом и правом торцах отдельного сектора для компонент перемещений принимались в виде u_k\ = u kj (j' = 1,2).

На рис. 10 показаны уровни перемещения на деформированной форме модели (перемещения увеличены в 5 раз). Профиль имеет перегибы в нижней части лопасти (ниже бандажной полки). Это является следствием ограничения перемещения по радиусу.

Рассмотрим детально область концентрации напряжений. Увеличим развертку уровней до 100 ^ 340 МПа и выполним зондирование значений в отдельных точках области (рис. 11, 12).

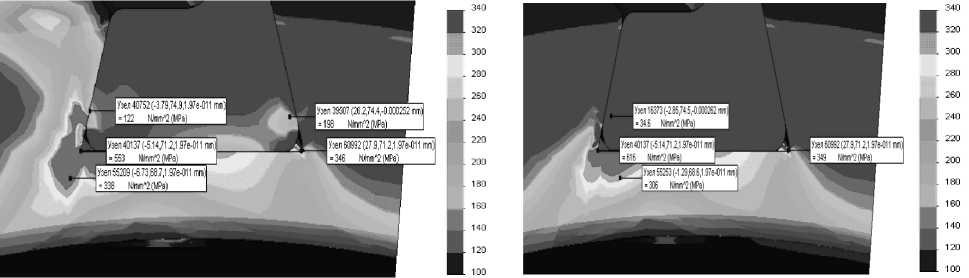
Рис. 11. Интенсивность напряжений главное напряжение

Рис. 12. Максимальное

Наибольшие напряжения развиваются в левом углу выреза. Их значения o imax = 553 МПа и a ₁ ^max = 616 МПа сопоставимы с пределом текучести титанового сплава o _т ^Ti = 937 МПа. Напряжения в основании лопатки существенно ниже, однако в отдельных точках превосходят предел текучести алюминиевого сплава о _т ^А1 = 69 МПа.

Хотя на основании значений напряжений в отдельных узлах нельзя делать вывод о возникновении зон разрушения, обнаруженные зоны концентрации напряжений являются потенциально опасными с точки зрения малоцикловой усталости (для полетного цикла нагружения). Исследование напряженного состояния в этих зонах на основе критериев многоосного усталостного разрушения позволит оценить долговечность рассматриваемого элемента конструкции ГТД.