Анализ неопределенности параметров модели разложения органического вещества: байесовский подход

Наличие громадных запасов органического углерода в виде гумуса почв свидетельствует о том, что почву следует рассматривать как мощный сток углерода. Учитывая возраст гумуса почвы, дискуссионным остается вопрос о размерах гумусонакопления в историческом масштабе. Для того чтобы установить, является ли интенсивное накопление углерода результатом прошлых эпох или процесс аккумулирования углерода продолжается в настоящее время, необходимо сочетание экспериментальных наблюдений с моделированием этого процесса на разных отрезках времени, используя динамические модели углеродного цикла в экосистемах

Разложение органического вещества в почве - это сложный многоступенчатый процесс. В то же время почва является важной составной частью лесной экосистемы и необходимо иметь количественные оценки основных потоков (например, эмиссии углекислого газа в атмосферу). Предложено большое количество моделей [1, 7], с той или иной степенью детальности описывающих процессы, происходящие в почве. При этом для каждой конкретной модели возникает задача определения параметров модели по экспериментальным данным.

Традиционный подход при решении такого рода задач состоит в применении метода (взвешенных) наименьших квадратов или максимального правдоподобия (если имеются основания выбрать соответствующую модель данных). Однако применение этих методов накладывает некоторые ограничения на класс моделей, для которых использование этих методов корректно. Кро- ме того, информация о точности (или надежности) оценок и адекватности модели данным может быть недостаточна, чтобы использовать откалиброванные параметры для целей прогноза поведения модели за пределами условий эксперимента.

В последнее время для решения задач идентификации параметров, калибрации и сравнения моделей используется байесовский подход, привлекательная сторона которого состоит в том, что он дает общий методологический подход, в рамках которого наиболее естественно решается проблема анализа неопределенности, связанной с неполнотой данных, сложностью модели и неустранимой вариабельностью параметров. Хотя байесовские методы были предложены достаточно давно, их применение сдерживалось трудностями вычислительного характера: в отличие от классических статистических процедур, аналитические решения для байесовской модели данных были известны только для небольшого ряда случаев. Однако развитие методов статистического моделирования и, в частности, использование метода Монте-Карло, основанного на применении марковских цепей (MCMC-моделирование), совпавшее с развитием средств вычислительной техники и программного обеспечения, сделало возможным применение этих методов во многих областях, в том числе в экологическом моделировании [8, 9, 10, 11].

В данной работе мы описываем опыт применения байесовских методов для оценивания параметров почвенной модели ROMUL по экспериментальным кривым разложения органическо- го вещества и сравниваем с результатами, полученными ранее методом максимального правдоподобия.

МАТЕРИАЛЫ И МЕТОДЫ

Экспериментальные данные. Общая схема опытов приводится в работе [3], непосредственно используемые нами данные - в работе [2]. Компостирование образцов проводили в контролируемых условиях (в темноте, при 20^оС и оптимальной влажности, т.е. 60% от полной влагоем-кости (ПВ) для минеральных компостов и около 300 весовых процентов для большинства растительных компостов. Учет потери массы компостов производили непосредственным взвешиванием воздушно-сухих образцов после 0,5; 1; 3; 6; 9 и 12 месяцев компостирования.

Модель ROMUL. При построении модели необходимо учитывать как сложность описываемых процессов, так и качество экспериментальных данных, по которым идентифицируются параметры модели. Конечный результат, как пра вило, представляет собой разумный компромисс между степенью детализацией модели и имеющимися данными. В качестве примера применения байесовских методов мы используем модель динамики органического вещества в почве ROMUL [1, 5]. Органическое вещество почвы в модели представлено тремя пулами: опад (L), подстилка (F) и органическое вещество минеральных горизонтов. Помимо цикла углерода в модели присутствует цикл азота. На каждом шаге, если предусмотрено сценарием, поступает свежий опад (L0). Далее, часть органического вещества в каждом пуле разлагается и переходит в следующий, часть минерализуется и выводится из системы. Количественные характеристики (скорости разложения и перехода) определяются системой дифференциальных уравнений, вид которых и подробное описание можно найти в [1, 5]. Так как имеющиеся данные соответствуют только первой стадии разложения, то мы имеем дело с частью модели, представленной в виде схемы (рис.1).

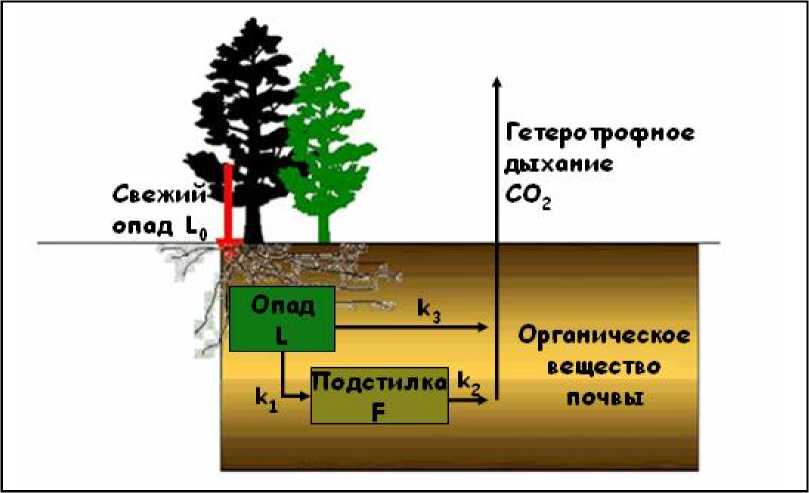
Рис. 1. Схема разложения органического вещества, соответствующая эксперименту

Дифференциальные уравнения, описывающие эту стадию разложения, зависят от трех параметров - к 1 , k ₂, к ₃, которые оцениваются по экспериментальным данным,

— = Lo - (к + к ) ■ L dt 0      1     3

— = к ■ L - k2 ■ F

dt ^{3        2}

.

Байесовское оценивание. В байесовском подходе параметры, которые нужно оценить по экспериментальным данным, трактуются как случайные величины. Подобное допущение может не соответствовать экспериментальной ситуации, но оказывается весьма удобным приемом. Это позволяет рассматривать неопределенность, связанную с оценкой параметров, в терминах вероятностных распределений. Кроме того, априорное распределение параметров p(к) может быть выбрано на основе литературных данных или проведенных ранее экспериментов, что способно улучшить качество оценивания в условиях недостатка эксперименталь- ного материала. Критическое отношение к байесовским методам основано прежде всего на том, что выбор априорного распределения зачастую субъективен. Однако, использование неинформативного равномерного распределения снимает остроту проблемы. Опишем коротко этот метод. Обозначим выборочные данные через D. Теорема Байеса связывает априорное распределение p(к) с апостериорным p(к | D) через функцию правдоподобия p (D | к)

p ( k i D ) — p ( D ^;,; ( k ) . p ^{( D} )

где p ( D ) - плотность вероятности, не зависящая от параметров, и которая обычно не участвует в вычислениях. Идея метода оценивания заключается в том, чтобы найти наиболее вероятные значения параметров к — ( к 1 , к ₂, к ₃) на основе наблюдавшихся в опыте величин D — ( d 1 , d ₂,... d n ). Другими словами, ищутся те значения параметров, при которых условная вероятность p ( к | D ) достигает максимального значения. К сожалению, вычислить апостериорное распределение в явном виде, как правило, невозможно из-за того, что p ( D ) - обычно сложно устроенная функция. Поэтому для нахождения апостериорной вероятности используется метод статистического моделирования, позволяющий получать выборки из распределения, известного с точностью до нормирующего множителя. В данной работе мы использовали алгоритм Метропо-лиса-Хастингса со случайным блужданием [6]. Идея этого алгоритма заключается в том, чтобы выбирать точки («блуждать») в наиболее вероятном подпространстве пространства параметров. Процедура оценивания на основе этого алгоритма состоит из следующих шагов. Прежде всего для каждого параметра экспертно определяется априорное распределение, и в отсутствии дополнительной информации предполагается, что параметры независимы. Следовательно, мы можем положить p ( к ) = p 1 ( к 1 ) • p ₂ ( к ₂) • p ₃ ( к ₃) .

Далее произвольно выбирается начальная точ-

Ъ-(0) _ ^Z^(0) Z^(0) Z^(0)A Кяипггпят ИЯ РТТРИЛЛТЛ-ка к — (к 1 ,к2 ,к3 ). Кандидат на следующую точку к * — (к 1, к 2, к 3) выбирается из распределения, описывающего случайное блуждание. Вычисляется отношение апостериорных вероятностей в = p(к*1 D) = p(D I к*) • p(к*) p (к | D)     p (D | к) • p (к)

•

Если в > 1 или , в > у где у - случайная величина, равномерно распределенная на (0,1), то точка принимается, т.е. k(1) = к *, в противном случае отвергается. После этого алгоритм возвращается к выбору нового кандидата. Получивша- яся таким образом последовательность точек (к(0), к(1),..., к(N)) после отбрасывания части первоначальных точек, соответствующей переходной фазе, определяет (выборочные) совместное p(к I D) маргинальные распределения p (к1 | D), котор ые могут дать представление о степени неопределенности параметров модели, после того, как был проведен эксперимент.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Результаты оценивания параметров модели мы рассмотрим на примере данных по разложению листьев осины. Условия эксперимента и предварительный анализ позволяют сделать предположение, что данные могут быть описаны гауссовским (нормальным) распределением, где среднее соответствует кривой убывания массы органического вещества m ( к ) , определяемой дифференциальными уравнениями (1), а дисперсия оценивалась по экспериментальным данным [2]. В качестве априорных распределений выбиралось равномерное распределение.

На рис. 2 и рис. 3 представлены совместные двумерные распределения и маргинальные распределения, соответственно, полученные после 5000 «успешных» шагов алгоритма. Выборочные распределения с достаточной полнотой описывают степень неопределенности параметров модели. В частности, на двумерных гистограммах хорошо видно, что апостериорное распределение не симметрично, параметры к_х и к ₃ ; к ₂ и к ₃ существенно скоррелированы. Сведения о высокой корреляции между параметрами полезны, так как могут служить основанием для редуцирования модели. Маргинальные распределения наиболее простой и наглядный способ представления результатов оценивания с помощью байесовского метода, когда параметрический вектор имеет высокую размерность. Форма распределения и сравнение с априорным распределением показывают какой из параметров требует специального внимания и, возможно, изменения модели или получения дополнительной информации.

Заметим, что оценки, полученные двумя способами, методом максимального правдоподобия и байесовским методом, близки. Это естественное следствие гауссовской модели ошибок и равномерного априорного распределения. На рис. 4 представлены кривые, «подогнанные» к данным двумя конкурирующими методами.

В таблице приведены результаты расчетов, сделанные для опытов по потере массы опадов различных типов. Результаты демонстрируют близкое соответствие подходов, максимального правдоподобия и байесовского оценивания.

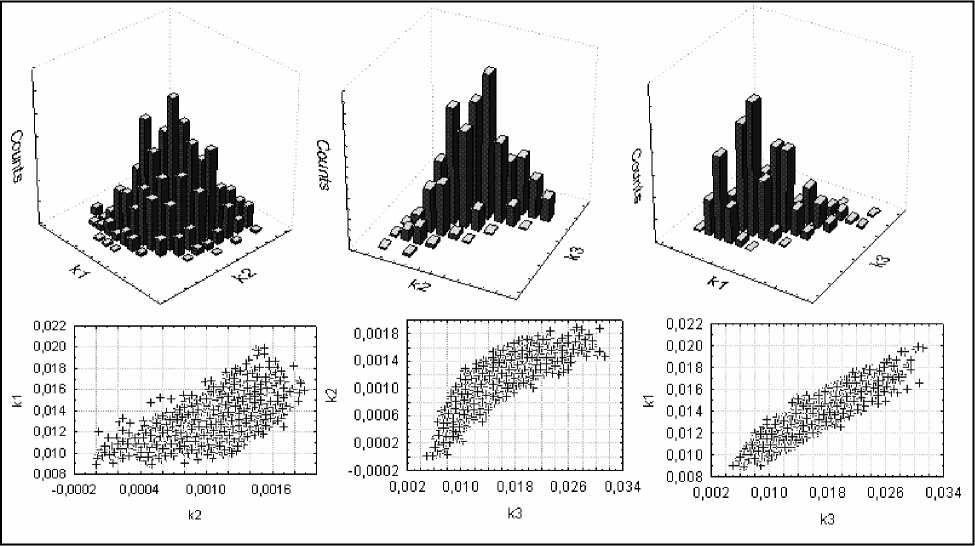
Рис. 2. Выборочные совместные распределения для параметров модели

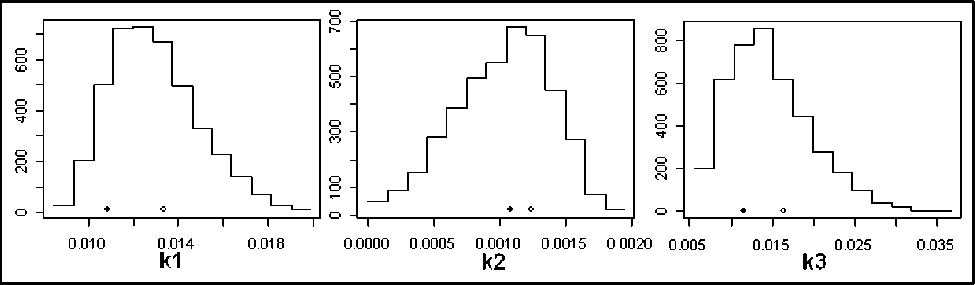
Рис. 3. Выборочные маргинальные распределения для параметров модели: символ (•) соответствует оценке максимального правдоподобия; и символ (°) - среднему маргинального распределения

ЗАКЛЮЧЕНИЕ

В практическом применении метод максимального правдоподобия (или метод наименьших квадратов) может быть предпочтительнее, если цель состоит в том, чтобы найти оценки параметров и подогнать модель к данным. Это преимущество связано, главным образом, с выигрышем в вычислениях, так как байесовский метод сопряжен с большой вычислительной работой. Метод максимального правдоподобия хорошо работает в случае, когда оценки модельных параметров имеют небольшую неопределенность. Однако в случае высокой неопределенности данных (небольшое число или высокая вариабельность) и, как следствие, плохой идентификации параметров преимущество, состоящее в оценивании распределения параметров и использовании априорной информации, делают байесов ский подход более привлекательным. Поскольку модели экологических систем часто оказываются многопараметрическими в то время как данные, необходимые для идентификации параметров ограничены, использование байесовских статистических процедур имеет большое значение.

Апостериорное распределение было оценено с помощью генерации выборок, основанной на методе Метрополиса-Хастингса, который разработан, чтобы получать выборки из распределений с неизвестной нормирующей константой. Преимущество байесовского метода состоит в том, что он позволяет описать неопределенность параметров в форме вероятностного распределения и байесовских достоверных областей. Кроме того, маргинальные распределения являются достаточно информативным способом описания свойств параметров модели в многопараметрическом случае.

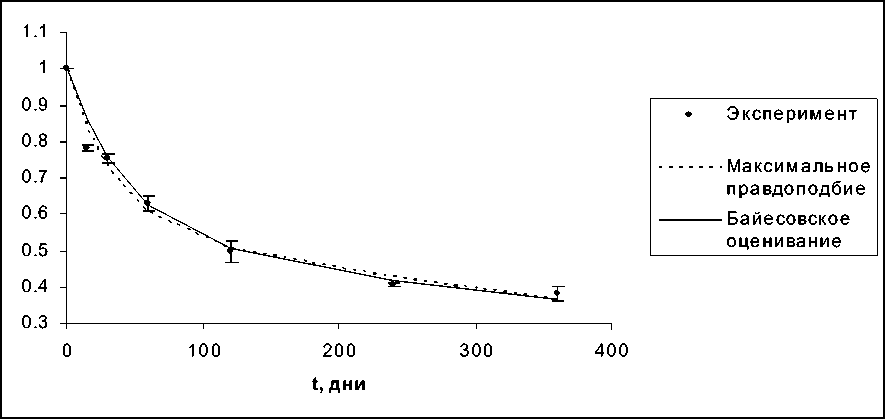
Рис. 4. Данные эксперимента по потере массы органического вещества и сглаженные кривые, рассчитанные методом максимального правдоподобия и байесовским методом

Таблица 1. Оценки параметров модели (1) методом максимального правдоподобия (МП) и байесовским методом, полученные по данным экспериментов с опадом разного типа

Опад	МП k 1	Маргинал ьное среднее k 1	Байес k 1	МП k 2	Маргина льное среднее k 2	Байес k 2	МП k 3	Маргина льное среднее k 3	Байес k 3
Папоротник Страусник ( Matteuccia struthiopteris)	0.02370 (0.00472)	0.03848 (0.016647)	0.02396	0.00121 (0.00017)	0.00122 (0.0002)	0.00117	0.0567 (0.0163)	0.10033 (0.05043)	0.05377
Папоротник Голокучник Линнея ( Gimnocarpium dryopteris)	0.02210 (0.00322)	0.23117 (0.094631)	0.02073	0.00093 (0.00014)	0.00114 (0.00014)	0.00086	0.0487 (0.0105)	0.64245 (0.25935)	0.04417
Ольха серая ( Alnus incana ) (листья)	0.01100 (0.00166)	0.008686 (0.000839)	0.00993	0.00112 (0.00027)	0.00066 (0.00032)	0.00071	0.0214 (0.00689)	0.01216 (0.00313)	0.01525
Рябина ( Sorbus aucuparia) (листья)	0.02180 (0.00147)	0.018342 (0.00109)	0.01766	0.00172 (0.00023)	0.00131 (0.00027)	0.00146	0.0213 (0.0032)	0.01461 (0.00226)	0.01501
Осина ( Populus tremula) (листья)	0.01340 (0.00137)	0.012914 (0.001933)	0.01201	0.00124 (0.00032)	0.00103 (0.00037)	0.00107	0.0164 (0.00414)	0.01465 (0.0049)	0.01353
Сосна ( Pinus sylvestris) (хвоя)	0.00815 (0.00045)	0.008544 (0.000645)	0.00815	0.00021 (0.0007)	0.00067 (0.0004)	0.00021	0.0042 (0.00141)	0.00556 (0.00139)	0.00416
Крапива ( Urtica dioica) (листья)	0.07360 (0.00748)	0.59593 (0.230423)	0.07363	0.0013 (0.00011)	0.00139 (0.00013)	0.00130	0.0746 (0.00954)	0.65121 (0.25071)	0.07456
Крапива ( Urtica dioica ) (стебли)	0.04540 (0.00339)	0.047649 (0.005646)	0.04356	0.0021 (0.00019)	0.00218 (0.00016)	0.00210	0.0416 (0.00511)	0.04497 (0.00746)	0.03925
Липа ( Tilia cordata) (листья)	0.03050 (0.00422)	0.031271 (0.007526)	0.02578	0.00169 (0.00017)	0.00156 (0.00021)	0.00164	0.0542 (0.0111)	0.05324 (0.01817)	0.04324
Мать-и-мачеха ( Tussilago farfara )	0.03840 (0.00405)	0.0404 (0.007278)	0.03866	0.00124 (0.00016)	0.00121 (0.00019)	0.00118	0.0489 (0.00764)	0.05144 (0.01274)	0.04776
Хвощ полевой ( Equisetum arvense)	0.06620 (0.00708)	0.067103 (0.009657)	0.06036	0.00104 (0.00018)	0.00099 (0.00018)	0.00096	0.0518 (0.0078)	0.0516 (0.00964)	0.04466
Зверобой ( Hypericum perforatum)	0.01490 (0.00192)	0.013658 (0.00138)	0.01391	0.0011 (0.00053)	0.00067 (0.00033)	0.00109	0.0138 (0.00475)	0.0104 (0.00246)	0.01210
Ромашка аптечная ( Matricaria recutita)	0.06030 (0.00648)	0.053392 (0.005432)	0.05969	0.00237 (0.00033)	0.00195 (0.0002)	0.00198	0.0409 (0.00726)	0.03127 (0.00504)	0.03712
Тимофеевка ( Phleum pratense)	0.04250 (0.00276)	0.039458 (0.003191)	0.04180	0.00236 (0.0003)	0.00205 (0.00021)	0.00226	0.0261 (0.00354)	0.02169 (0.00304)	0.02492