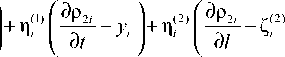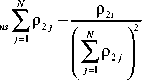Анализ нестационарных режимов в системах контроля и управления распределенными процессами

Системы контроля и управления в химических техно логических процессах часто создаются на основе анализа лишь статических характеристик, что не повышает эффективность их функционирования.

Контролируемые и управляемые параметры химикотехнологических объектов носят явно выраженный пространственно распределенный характер. Специфика распределенности управляемых процессов настолько велика, что формальный перенос хорошо разработанной теории управления объектами с сосредоточенными параметрами на распределенные системы не имеет успеха.

При моделировании и управлении процессов с распределенными параметрами возникает вопрос об исполь зовании распределенного контроля и распределенного управления. При этом практический интерес при создании высококачественных систем управления представляет такой подход, при котором улучшение динамических свойств управления достигается за счет рациональной системы контроля. Неравноценность информации о со стоянии управляемого процесса в различных точках объекта и ее большое количество обусловливает поиск оптимальных оценок состояния управляемого процесса.

Рассмотрим непрерывный процесс взаимодействия двух противоточно движущихся сред в тепломассообмен ном аппарате с пространственно распределенным воздействием. Для этого объекта поставлена и решена зада ча оптимального распределенного контроля на основе метода вариационного исчисления. Получены необходимые условия оптимальности весовых функций распределенного контроля. Эти условия используются для построения численного алгоритма расчета оптимальных весовых функций.

Исходя из закона сохранения количества тепла или массы, в рамках гипотез, принятых в работе [1], рассмотрим систему уравнений, описывающих этот процесс:

Э0 , д ( ш _| 0 _| )

—— + —---= ж, (/, t)(02 -0,), д t        дl                                        ^1^

~+~ + ^ Д= ^2 (^’ t)(01 -02 ) + /(I, t), д t        д l где 0. = 0. (Г, t), г = 1,2 — функция распределения температуры или концентрации; to. = щ.(I, t), г = 1,2 — скорость движения первой и второй сред соответственно;/(Г, t) — функция внешнего воздействия; ж. = ж. (Г, t), г = 1,2 — коэффициенты, характеризующие свойства взаимодействующих сред.

Здесь внешнее воздействие приложено в т промежуточных точках и может быть представлено в виде m f (l, t ) = Z Xj(l )vj(t).

j =1

В качестве функции распределенного внешнего воздействия возьмем функцию

X j ^{( l} ) = '

a ( l - l j ) b e ⁽ l ^- l^{j )} , l e [ 0, l j ,

0, l e [lj, l J, где Г — координата точки приложения внешнего воздействия; а = 738,91; b = 2; с = 20.

Дополним систему уравнений (1) следующими на чальными и граничными условиями:

0i (l,0) = 0, i = 1,2,(2)

01 (0, t) = 0,88 (t), 02 (1, t) = 0288 (t),(3)

где 0 _1вх( t ), 0 _2bx ( t ) — заданные функции.

Функционал качества имеет вид

T

I = j[e* (1, t)-01 (1, t)J dt, где T — фиксированное время процесса управления; 0/(1, t) — заданное значение регулируемой величины; 01вх(1, t) — регулируемая величина.

Имеется возможность подачи на объект ( т + 1) управляющих воздействий: приу = 0 — за счет изменения граничных условий на входе второй (регулирующей) среды v ₀( t ) = 0 _2bx ( t ); приу = 1, _, т — за счет промежуточных внешних воздействий v . ( t ).

Таким образом, получаем ( т + 1) — контурную систему автоматического регулирования. Функции управляющих воздействий v . ( t ),у" = 0,..., т представим в виде

1                       1

v j ( t ) = j u j ( t , т ) j 0 ₁ ( l , т ) g j ( l ) dld t, j = 0,..., m , ⁽⁵⁾ 0             0

где V( ( t ) — операторы используемых управляющих устройств (в данном случае интегральные) с заданными ядрами и ( t , т ), определенными в треугольнике 0 < т <  t T [5];

ф . ( t ) = j 0 ₁ ( l , т ) g j ( l ) dl — воздействия на входе регуля- 0

торов, характеризующие состояние объекта управления и выражающиеся через весовые функции распределенного контроля g . ( х ).

Итак, задача оптимизации системы управления формируется следующим образом: найти такие весовые функции g(Г), при которых значение функции состояния 0 ₁(1, t ) минимизировало бы функционал качества (4).

Лемма 1. Сопряженная система уравнений и необходимые условия оптимальности имеют вид

------- + to ₁ ( ^l , t )     - Ц ( ^l , t ) Ж [ + Ц 2 ( i , ^t ) № 2 -д t                    д l

1 T m j jZ ^2 (^ t1 ) ж (^) Uj (t1, t) gj (1) dt1dk +      (6)

0 t ^{j = 1}

+ j ш , ( 1, t , ) ц ₂ ( 1, t , ) и о ( t , , t ) dt , g о ( I ) = О, t

• - „ (l, t )^M - Ц2 (l, t) «2 + Ц2 (I, t) ^ = 0, (7) d td

• 2 [® ^; — 0 , ( 1, t )^] - ш , ( 1, t ) ц , ( 1, t ) = О,

^2 (0, t)ц2 (0, t) = 0, ц, (l, T) = О, ц (l, T) = 0, (8) Lti (О,, p2 ) = jЦ2 (^ t)„2 (1, t)j«0 (t, T)0, (l, T)dTdt = 0, (9) 00

Lj (0,, ц, ) = jjц, fe t)aj (^)jиj (t, t)0, (I, t)dтdtd§ = О, 0 00

j =,,..., m.(10)

Метод решения системы уравнений таков:

• 1)    задают начальные приближения весовых функций g_J⁰(. I );

• 2)    если g" ( Г ) известны, то по системе уравнений (1) и граничным условиям (2), (3) находят О , " = О , " ( / , t ) и по сопряженной задаче (6)^(8) определяют ц" = ц"( Г , t ), i = 1,2;

• 3)    далее полагают g _О^опт - g ₀ " - т L ₀( О , " , ц ₂ " ), g . ^опт = g." - - т L ₀( О , " , ц ₂ " ), т> 0, и =0,1,2, ...;

• 4)    предельные значения весовых функций дают решение задачи.

Для численной реализации задач (1)^(3), (6)...(10) построена явная консервативная конечно-разностная схема, аппроксимирующая исходную систему уравнений (1) с первым порядком на равномерной сетке. При этом справедлива лемма 2.

Лемма 2. Левые части конечно-разностных аналогов уравнений (9), (10) представляют собой градиент аппроксимированного функционала качества (4).

Следовательно, для решения задачи может быть использован градиентный метод [2].

Приведем примеры расчета систем контроля по разработанной программе: кривую разгона и оптимальную переходную характеристику в одноконтурной схеме регулирования с весовой функцией оптимального контроля g ₀( Г) (рис. 1) и кривую 2, соответствующую этой функции (рис. 2), а также кривые оптимального управления (рис. 3) и соответствующие функции распределенного контроля с подачей управляющих воздействий в точки, распределенные по длине аппарата (рис. 4).

0,(14)                    /"=0,493

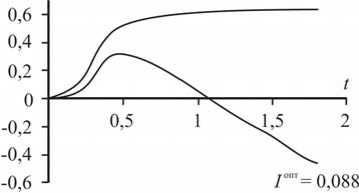
Рис. 1. Изменения температуры в переходном режиме и при оптимальном контроле с весовой функцией g ₀ ( х )

Рассмотрим получение оптимальных весовых функций распределенного контроля, дающих оценку контролируемых параметров управляемого процесса нестационарной массопередачи для промышленной ректификационной колонны К-101 [2].

Исходя из закона сохранения количества тепла и массы, в рамках гипотез, принятых в [1], рассмотрим следующую математическую модель управляемого процесса:

^ - c⁶-^ = k y ⁽ y - y ^; н,

^ + c2 ^dli = ky (y -У; ) + Ф2, i =,,...,N,(11) Q = {(l, t)/0 < l <,, 0 < t < T}, где p,., p2. - средние плотности компонентов разделяемой смеси; Ф,, Ф2 - функции внешнего воздействия;^.(Г, t), у* (/) - концентрация и равновесная концентрация в паровой фазе; с,, с2 - скорости жидкой и паровой фаз; к^ - коэффициент массопередачи.

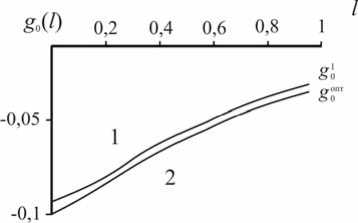
Рис. 2. Начальная g ₀ ’ и оптимальная g ₀ ⁰ ” весовая функция распределенного контроля

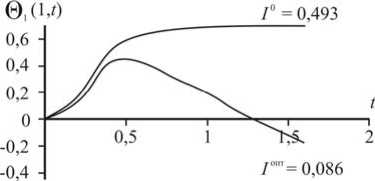
Рис. 3. Изменения температуры в переходном режиме и при оптимальном контроле с весовыми функциями g ₀ , g ₄

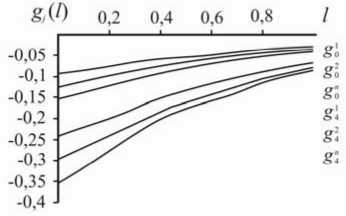
Рис. 4. Начальные g ₀\ g ₄ ^] и оптимальные g ₀ ” , g ₄ ” весовые функции распределенного контроля

Известна также связь концентраций с плотностями: х,=       , y=       .

£ р „

=,

Система (11) содержит 2 N неизвестных функций и столько же уравнений. Дополним эту систему начальными и граничными условиями:

Р,i(l,0)=Ф„.(l), P2i (l,О) = ф2,- (l), где ф,.(I), ф2.(Г) - заданные функции. При I = 0

Р2,. (0, t) = c2-1V0 (t) y, (0, t), dy, (0, t)

H ------= Ci xk     dt 1

t

P i i ( ⁰ t ) ^— У , ( ⁰ t ) Z P i j ( ^0, t )

j =1

У , ( 0,0 ) = ^i ^{( 0 )} ; ^j -W j =i

N где V0 (t) = ciZPij (0, t) —F(t) + D(t), /=1 j=i

P i , ( 1, t ) = c i ^{- 1} L D ( t ) x , ( 1, t ) ,

,

H x D ( t )

dx i ( 1, t )

= c ² dt

p2i (l, t)—li (Л t)Zp2j (Л t), j=i x,(1,0) =

EMO j=i

HT^ = c2ZP2j(l. t) — LD (t) — D(t), HxD (0)= «. (15) dt

Система уравнений (11).. .(15) описывает процесс нестационарной массопередачи в ректификационной колонне с переменным уровнем в дефлегматоре. Для того чтобы колонна неограниченно не исчерпывалась и не переполнялась, введем следующее условие:

J ( F ( t ) — D ( t ) — W ( t ) ) dt = 0,             (16)

где T- заданное время управления. Корректность этой краевой задачи показана в [2].

Сформулируем задачу оптимального распределенного контроля. В качестве цели оптимизации можно поставить требование достижения наименьшего среднеквадратичного отклонения регулируемой величины х (1, t ) и (или) у . (0, t ) вверху и внизу колонны (это наилучшее качество целевого продукта):

T Г                                2                                     ² 1

• ⁵    = Л£ k i [ x , ( i, t ) "® 1 - ] ⁺ £ kA [ y i ( 0, t ) —© 2 , ] [ dt . (17)

0 [ j = i                                      j = i                                    J

Нами также исследованы и другие критерии оптимизации: производительность аппарата, критерий разделительной способности и др.

Рассмотрим замкнутую систему регулирования с управлением D(t). Имея ввиду использование распределенного контроля в паровой фазе, на вход регулятора [2], регулирующего D(t), поступит сигнал lM

ф ( t ) = JZ y s ( l ’ t ) g s ( l ) ^dl ’

0 s=i где M - количество контролируемых параметров, выбранных из ys(/, t); gs(/) - весовые функции распределенного контроля, дающие оценку контролируемым параметрам в автоматической системе регулирования. Управляющее воздействие D(t) в случае интегрального регулятора будет иметь вид tlM

D ( t ) = J u ( t , t ) JZ y s ( l , т ) g s ( l ) dld T ,

0            0 s=i где и(t, т) - заданная функция, характеризующая регуля тор.

При контроле за параметрами в жидкой фазе задача оптимизации рассматриваемой системы управления формулируется аналогично. Она состоит в нахождении таких весовых функций распределенного контроля g(/), которые в силу системы уравнений (11).. .(16) минимизируют функционал качества (17).

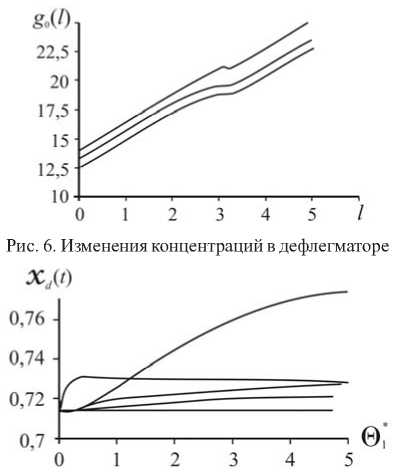
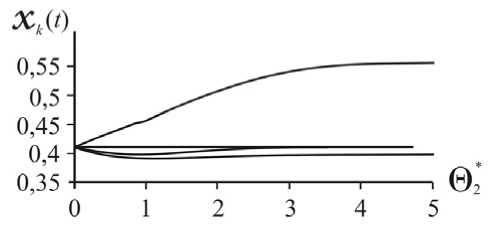
Переходя к нормальной форме, получим следующую систему дифференциальных уравнений, описывающую управляемый процесс [2]:

d p iL = ^ ( ⁱ⁾ + k y ( y , — y i • ) +Ф 1 . X i , 'V = ^ , o t                                          d l

= — cG2) + kvU — y,*)+Ф2 = Y,     = G2), d t          21 y(i i)       2      ' d l ‘

0 <  l <  i, 0 <  t <  t , при краевых условиях:

P2i (0, t) — V (t) y , (0, t) c—i = 0, dyi (0, t) = ci dt H xk

N

Pii (° t)— y, (° t )Z Pij(0, t) j=i y,(0,0)= NV2i(0) , 0

Pi, (!, t) — LD (t) x, (1, t) c—i = 0, dxi (i, t) = c2

dt H xD ki,

Di^,

dHxD (t) dt

X, (i,0) =            ,

S»ij(i) j=i

N

" = ^c2 ^^2 j⁽ⁱ, t^{) —}LD⁽t^{) —}D⁽t) ⁼HD , j=i

HxD (0)= «i, 0 < t < T, l = i, с начальными условиями (13).

Для получения необходимых условий оптимальности рассмотрим вспомогательный функционал

I = I_i+12 = JJ Ldtdl + J ldt,

Q        d Q где dQ - граница области Q;

N

1^=z]< (ⁱ⁾

,=i i 1 ^ t

(2) f ^dP2i

—^ (ⁱ⁾+

d l

N i=z{k"(xi(i,t)—0;i)^+k-'”(y(0. t )—©;,) + =i

+^D) (Pi i C1, t)—LD (t) xi C1, t)c—i)+

(2) ^fdxi (1, t)

+Л Di             X Di dt

V

_x(2) f dyi⁽⁰, t)

1 '

^

⁺Ai) (P2i (⁰t)^—V0 (t)у, (⁰t)^c2 ) ⁺

f dH (t)

xD dt

^^^^^™

^

’

здесь ^.⁽¹⁾, ^.⁽²⁾, ц.⁽¹⁾, ц,⁽²⁾ - функции, определенные на Q; %_D.⁽¹⁾, %_o.⁽²⁾, %д)³*, %j.⁽¹⁾, %j.⁽²⁾ - функции, определенные на dQ.

Пусть g(/) - оптимальные весовые функции, pt., р2.-оптимальноерешение задачи (11)_(16), соответствующее g(/). Тогда, найдя вариацию 81= 811 + 812 и используя аргументацию вариационного исчисления, будем иметь следующую сопряженную систему дифференциальных уравнений относительно £., ц., %D.(2), %k.(2) (^.(2) и ц.(2) выражены через £.(1) и ц.(1) и обозначены £. и ц., аналогично исключаются %D(‘>, %k('>):

^d--. '^= d t     ¹ dI

N

«2 E P2j j=1

N

PE P1j j=1

N

(5i - n,)E(^ k - ^k)

k=1

N

PikPkE P1 j- - Pk j=1

^дй, „ ^дй i _ „ d t²d l ²

N

(й1 - 5, )+E p« (^k -k=1

й k) -Nk

p E P1j

N

^-E i k (°, t)Ук (о, t)

k=1

j =1

M

E gs (i)

s=1

,(18)

,       [1, s = i, kns =)n

[0, s ^ i,

Tг                              .1

Ls (l) = J ^к(^-E Пk (°, t) Ук (°, t) ys (l^,t) dt

0 L

,

^i (l, t) = °, 4i(l, t) = °,                 (19)

• 2)    если g_n⁰( 1) известны, то по системе уравнений (11)^(16) находят p_t.⁽">, р₂.⁽">, а по сопряженной задаче (18)_(21) определяют ^., ц ., %_k.²⁽">, %_D²⁽">, %_D.³⁽">;

• 3)    далее полагают g"⁺¹ = g" - тL ;

• 4)    предельные значения весовых функций дают решение исходной задачи.

Выражение (22) - это градиент вспомогательного функционала I. Можно показать, что это выражение есть градиент оптимизируемого функционала (17). Следовательно, для численной реализации метода используется градиентные методы [2].

Приведем графики оптимальных весовых функций распределенного контроля g_s(1) (рис. 5) и соответствующие концентрации первого (легколетучего) компонента в дефлегматоре (рис. 6) и в кубе (рис. 7) промышленной ректификационной колонны К-101. За контролируемый параметр принята концентрация легколетучего компонента в паровой фазеу₁( 1, t). Кривые х₁(1, t) иу₁(0, t) соответствуют начальной весовой функции g(1) = 0 при возмущении легколетучего компонента в сырье на + 20 % от исходного значения, кривая 1 - минимальному отклонению концентрации х₁(1, t), кривая 2 - минимальному от-клонениюу₁(0, t), кривая 3 - минимальному отклонению х₁(1, t) иу₁(0, t) одновременно.

-k⁽²⁾                 N

—==4-⁽o, t) cE Р1_У—W⁽t)

^-t               l j=1

x) E P2 j

------2k^ (yi(°, t)-©2i),       (20)

к⁽2)

^i (°, t) =

H x_k

Eyk (°,t)| ^ - nk (0,t)'.

^k=1             HXk

kk2) = °, 0 < t< T, l = 0,

N n (2)                   C21-m E p2 j (1, t)

= ^i (1, t)L- (t)----2kP (Xi (1, t)-©*i), dt                          H.D (t )

kD) (T) = °,                    (21)

niC¹. t ) =

Di

H.D (t)

Exk (1. t) x™ k=1___________________ H.D (t)

+k⁽3,

Рис. 5. Зависимости оптимальных весовых функций g_s(Г)

d⁽³⁾      N       Г                   N          1 /

—= = ^-E ^C2^5 P2 i^(1,t )^-xi^(1,t )E P2 j^(1,t ) /^HD^{( (}t )’

^-t        i=1        l                       j=1           J/

k(²⁾ = °, 0 < t< T, l = 1,              (22)

где Pk = Ak T2 + Bfc т + Ck - парциальное давление для к -го •   dP компонента; P = ——; т - температура в колонне; A , k dp2j

B_k, C_k - коэффициенты, определяемые по экспериментальным данным методом наименьших квадратов [2]; P - общее давление в колонне; 5 - множество индексов контролируемых параметров.

Метод решения системы уравнений заключается в следующем:

1) задают начальные приближения весовых функций g_s⁰( 1);

Рис. 7. Изменения концентраций в кубе

Для первой схемы регулируемая величинах₁(1, t) близка к требуемому значению ©₁₁‘, функционал качества _sопт ₌ 4 . 10-4. Содержание этого же компонента в кубе

колонныу₁(0, t) имеет наибольшее отклонение от заданного значения 0₂₁‘.

При оптимизации качества нижнего продукта в колонне отклонение регулируемой величиныy₁(0, t) от заданного значения 0₂₁‘ уменьшается по сравнению с первой схемой регулирования, однако вверху колонны зна-чениех₁(1, t) увеличивается. При этом s^опт = 0,114.

Для критерия оптимизации отклонений одновременно верхнего и нижнего продуктов кривая переходного процессах₁(1, t) совпадает с аналогичной кривой во второй схеме регулирования, а криваяy₁(0, t) также незначительно отличается от соответствующей кривой во второй схеме и s^опт = 0,729.

В случае распределенного контроля за содержанием первого компонента в жидкой фазе при минимизации отклонения х₁(1, t) от заданного 0 ‘ s^опт = 4 ■ 10 ². При оптимизации отклоненияy₁(0, t) от 0 ‘ s^опт = 9 ■ 10 0 При одновременной минимизации отклоненияy₁(0, t) их₁(1, t) от0₂₁^,и0₁₁^,s 0,325.

В заключение можно сделать следующие выводы: сформулирована задача оптимального контроля за системами с распределенными параметрами, получены необходимые условия оптимальности весовых функций распределенного контроля, проведено численное исследование оптимальных систем контроля для промышленной ректификационной колонны, показана эффективность распределенного контроля.