Анализ несущих поверхностей экранопланов

Проектирование экраноплана связано с решением проблемы устойчивости во всем диапазоне полетных скоростей и отстояний, получением высокого аэродинамического качества и коэффициента подъемной силы аппарата. Одним из методов решения данной проблемы может быть выбор соответствующей формы несущей поверхности экраноплана.

На сегодняшний день наиболее широко распространены две формы несущей поверхности экранопланов -прямоугольное крыло, треугольное с обратной стреловидностью и характерным отрицательным углом поперечного V. Определенный интерес также представляет крыло с характерным положительным углом поперечного V (рис. 1).

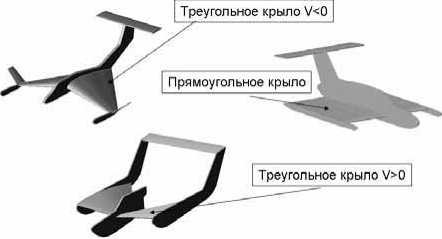
Рис. 1. Основные формы несущих поверхностей экранопланов

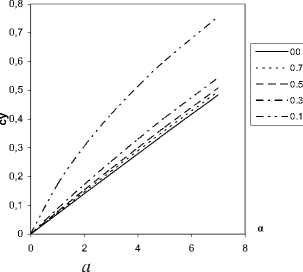
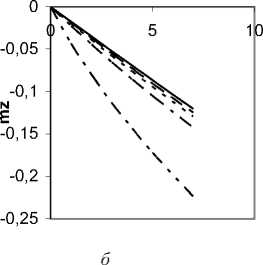
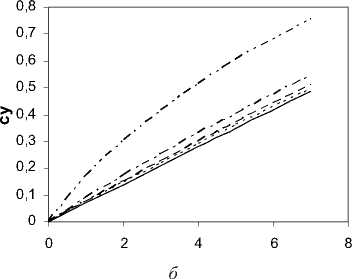
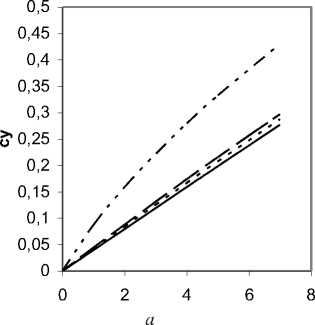
Методом дискретных вихрей [1; 2] были решены линейные задачи безотрывного обтекания идеальной жидкостью прямоугольного крыла, треугольного с характерным отрицательным углом поперечного V и треугольного с положительным углом поперечного V малого удлинения. Получены числовые значения коэффициента подъемной силы с_у(а, h) и коэффициента продольного момента m_z ( а , h), относительной координаты фокуса х^ а , h) для различных углов атаки и относительных высот, безразмерная аэродинамическая нагрузка на крыло. Графики соответствующих зависимостей с_у =У( а , h), m_z =У( а , h) и х = ( а , h) приведены для треугольного крыла малого удлинения с характерным отрицательным углом поперечного V (рис. 2), прямоугольного крыла (рис. 3) и треугольного с положительным углом поперечного V (рис. 4).

По полученным числовым значениям коэффициента продольного момента методом интерполяции функции нескольких переменных получены функциональные зависимости с_у =ф(б, К) и m_z =f(б, h) для треугольного крыла с углом поперечного V< 0:

с_у = 0,264 а- 1,204 4 а Л -

• - 0,01197 а ² + 0,119 57 а ² h + 2,715 а h ² -

• - 0,212 3 а ² h ² - 0,003 69 а ³ -

• -0,003 41а3h - 2,633 4аh3 + 0,018а3h2 +

  + 0,0911а²h³- 0,007 4а³h³+

+ 0,000 55 а ⁴ - 0,000 82 а ⁴ h + 0,943 9 а h ⁴;

т z = - 0,066 8 а + 0,304 2 а к +

+ 0,00197 а ² - 0,019 а ² h - 0,703 9 а h ² +

+ 0,033 7 а ² h ² + 0,000 617 а ³ +

+ 0,000 43 а ³ h + 0,707 2 а h ³ - 0,002 7 а ³ h ² -

• -    0,014 4 а ² h ³ + 0,0011 а ³ h ³ -

• - 8,873 • 10 ^{- 5} а ⁴ + 0,00013 а ⁴ h - 0,260 6 а h ⁴ .

Аналогичные выражения для коэффициентов можно получить для плоского крыла прямоугольной формы в плане малого удлинения:

с_у = 0,243 5 а- 1,226 6 а к -

• - 0,003 3 а ² + 0,0721 а ² h + 2,843 3 а h ² -

• - 0,134 4 а2h2 - 0,004 5 а3 +

+ 0,002 35 а ³ h - 2,849 а h ³ + 0,008 3 а ³ h ² +

+ 0,050 7 а ² h ³ - 0,002 27 а ³ h ³ +

• + 0,000 54 а ⁴ - 0,000 84 а ⁴ h + 1,054 76 а h ⁴ ;

т z =- 0,070 6 а + 0,378 7 а к -

• - 0,000 95 а ² - 0,006 5 а ² h - 0,908 3 а h ² +

  + 0,0141 а ² h ² + + 0,001 25 а ³ -

  • - 0,00192 а ³ h + 0,945 1 а h ³ + 0,000 367 а ³ h ² -

    • -    0,002 7 а ² h ³ — 0,000 7 а ³ h ³ -

    • - 0,00012 а ⁴ ++ 0,000 2 а ⁴ h - 0,3 60 7 а h ⁴ .

Для треугольного крыла малого удлинения с углом поперечного V > 0 интерполирующие многочлены с ~/(а. h) и mz =Да, h) имеют вид су = 0,127 8а- 0,520 8ак -

• - 0,005 а ² + 0,048 8 а ² h + 1,149 9 а h ² -

• -    0,086 2 а ² h ² - 0,00144 а ³ -

• -0,001 47а3h -1,102 6аh3 + 0,007 3а3h2 +

+ 0,037 а ² h ³ - 0,003 05 а ³ h ³ +

• + 0,000 22 а ⁴ - 0,000 32 а ⁴ h + 0,3914 а h ⁴ ;

т _z =- 0,029 9 а + 0,125 а к +

• + 0,000 83 а ² - 0,007 3 а ² h - 0,282 6 а h ² +

  + 0,012 7 а ² h ² + 0,00019 а ³ +

  • + 0,000 24 а ³ h + 0,280 а h ³ - 0,00107 а ³ h ² -

  • - 0,005 5 а ² h ³ + 0,000 46 а ³ h ³ -

• -2,953 • 10-5 а4 + 4,33 • 10-5 а4 h - 0,102 а h4.

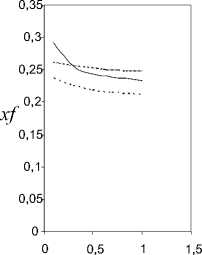
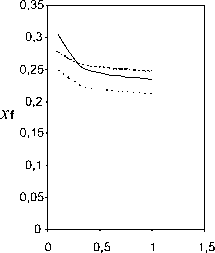
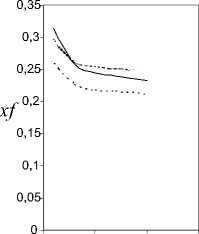
Также построены интерполирующие зависимости для относительной координаты аэродинамического фокуса х=(б, Л)(рис. 5).

Для треугольного крыла с углом поперечного V < 0, зависимость изменения относительной координаты аэродинамического фокуса составит

Xf ₍ v < 0) = 0,144 - 0,136 а- 1,879 4 h +

+ 2,323 а h - 0,022 2 а ² +

+ 5,7117 h ² - 0,454 2 а ² h -

• - 7,250 5 а h ² + 1,705 6 а ² h ² + 0,016 7 а ³ -

  • - 5,253 h ³ + 0,00516 а³ h +

+ 6,166 5 а h ³ - 0,166 7 а ³ h ² -

оо

--0.7

■ 0.5

— - 0.3

- — 0.1

Рис. 2. Численные результаты решения линейной стационарной задачи безотрывного обтекания треугольного крыла малого удлинения с углом поперечного У<0 вблизи экрана: а - коэффициент подъемной силы треугольного крыла

У <0; б - коэффициент продольного момента треугольного крыла У < 0

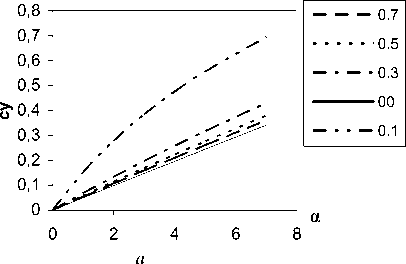
Рис. 3. Численные результаты решения линейной стационарной задачи безотрывного обтекания прямоугольного крыла малого удлинения вблизи экрана: а - коэффициент подъемной силы прямоугольного крыла; б - коэффициент продольного момента прямоугольного крыла

-------00

.......0.7

----0.5

-----0.3

-----0.1

• - 1,010 7 α ² h ³ + 0,097 21 α ³ h ³ -

• - 0,001984 α ⁴ + 1,4916 h ⁴ +

  + 0,00535 α ⁴ h - 1,4916 α h ⁴ ;

для прямоугольного крыла зависимость х = (а, Л) будет иметь вид xf ([]) =0,2736+0,032α-

• - 0, 0511 h - 0, 273 4 α h - 0, 0011 α ² -

  - 0,05128 h ² + 0,0382 α ² h +

  + 0,6759 α h ² - 0,1104 α ² h ² -

  • - 0,00083 α ³ + 0,0461 h ³ - 0,001 α ³ h -

• - 0, 561 3αh3 + 0, 095α3h2 +

  +0,063 4α²h³-0,0055α³h³+

  +0,000105α⁴+0,0073h⁴-

• - 0, 000 26α4h + 0,143 3αh4;

для треугольного крыла малого удлинения с углом поперечного V> 0 получим xf(v>0)=0,1734+0,0717α+

+ 0,32 h - 0,3533 α h - 0,0195 α ² -

• - 0, 865 3 h ² + 0, 066 7 α ² h +

  + 0,6998 α h ² - 0,0914 α ² h ² +

  + 0,00249 α ³ + 0,99 h ³ - 0,0064 α ³ h -

  • - 0,6043 α h ³ + 0,009 α ³ h ² +

    + 0,03178 α ² h ³ - 0,003466 α ³ h ³ -

    • - 8,411 ⋅ 10 ^{- 5} α ⁴ - 0,4439 h ⁴ +

+ 1, 067 ⋅ 10 ^{- 5} α ⁴ h + 0, 223 3 α h ⁴ .

Как видно из полученных результатов, одно из существенных преимуществ треугольных крыльев малого удлинения с углом поперечного К> 0 (К< 0) меньшая чувствительность координаты положения фокуса крыла к изменению высоты движения

⎛⎜ ∂ x ⎞⎛∂ x ⎞ ^f ⎟^<⎜ ^f ⎟ ^, ∂ h ∂ h ⎠ ∆ ⎝⎠ []

при а = const.

Кроме того несущая способность треугольного крыла малого удлинения с углом поперечного V< 0 оказывается больше крыла прямоугольной формы в плане ^⎛ ⎜ ^{∂ cy ⎞} ⎟> ^⎛ ⎜ ^{∂ cy ⎞} ⎟ , ∂α ∂α ⎝⎠ V <  0 ⎝⎠ []

при h = const.

Однако отсутствие шайб и положительный угол поперечного V для треугольного крыла приводит к тому, что часть воздуха перетекает от корневой хорды к концевой, образуя присоединенный поперечный вихрь, который сходит с задней кромки крыла в виде свободного вихря, в результате чего давление в подушке под крылом снижается, уменьшается подъемная сила по сравнению с треугольным крылом с положительным углом поперечного V:

1 >R 1

⎝ ^∂α ⎠ ∆     ⎝ ^∂α ⎠ ∆

V < 0             V > 0

при h = const.

Увеличить несущую способность треугольного крыла малого удлинения с углом поперечного V > 0 можно поставив шайбы. Для треугольного крыла с положительным углом поперечного V была решена линейная стационарная задача безотрывного обтекания, методом дискретных вихрей получены значения коэффициента подъемной силы с_у( а , Л) и коэффициента продольного момента т(а, Л), координаты центра давления, х_т( а , Л) для различных углов атаки и относительной высоты 0,1 Ъ₆ с шайбами шириной 0,08Ъ₆ и без шайб (рис. 6).

Используя известные критерии Иродова для оценки устойчивости экраноплана [3; 4]

x f в >  х т ( m Z < 0)

^и X f в >  X fh

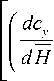
⎠ m_z = 0 δ= const

< 0

можно оценить диапазон относительных высот и углов атаки, в которых данная несущая поверхность будет устойчива.

Так, из функциональных зависимостей для относительной координаты аэродинамического фокуса л^необходи-

-------00

.....0.7

---0.5

----0.3

----0.1

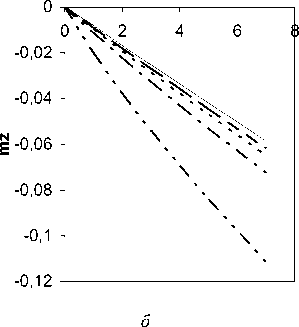
----------00 ---0.7

.....0.5

— - — ■ 0.3

— - - — 0.1

Рис. 4. Численные результаты решения линейной стационарной задачи безотрывного обтекания треугольного крыла малого удлинения с углом поперечного V> 0 вблизи экрана: а - коэффициент подъемной силы;

б - коэффициент продольного момента

мо получить выражения для фокуса по высоте и по углу атаки.

Данные выражения аппроксимируем по результатам интерполяционных многочленов х = ( а , Л) для различных отстояний и углов атаки методом наименьших квадратов [5].

Тогда условие устойчивости для треугольного крыла мало удлинения с углом поперечного V< 0 примет вид

⎧- 0,0668 + 0,3042 h +

^⎪ _⎪ + 0, 003 94 α - 0, 038 α h -⎪ _⎪ - 0,7039 h ² + 0,0674 α h ² +

⎪+ 0,001851 α ² + 0,00129 α ² h + ^⎪ _⎪ + 0,707 2 h ³ - 0,0081 α ² h ² - ^⎪ - 0,0288 α h ³ + 0,0033 α ² h ³ -

⎪

- 3,549 ⋅ 10 ^{- 4} α ³ +

⎪

^⎪ _⎪ + 5,2 ⋅ 10 ^{- 4} α ³ h - 0,2606 h ⁴ < 0, ⎪ 0,253 + 0,165 α- 0,3227 α ² - ^⎪ ⎪- 2,972 4 α ³ + 14,72 α ⁴ -

^⎪ _⎪ - 2,1975 h + 8,305 h ² -⎪⎩- 11,568 h ³ + 5,309 h ⁴ > 0;

для прямоугольного крыла малого удлинения условие запишется в виде следующей системы неравенств:

• - 0,0706 + 0,3787 h -

• ^⎪ _⎪ - 0, 001 9 α - 0, 013 α h -⎪ _⎪ - 0, 908 3 h ² + 0, 028 2 α h ² + ⎪+ 0,00375 α ² - 0,00576 α ² h + ^⎪ ⎪+ 0,9451 h ³ + 0,000501 α ² h ² - 0,0054 α h ³ - ^⎨ _⎪ - 0, 002 1 α ² h ³ - 0, 000 48 α ³ + ^⎪ _⎪ + 0,0008 α ³ h - 0,3607 h ⁴ < 0, ⎪ 0,251 + 0,2315 α- 1,8183 α ² + ^⎪ ⎪+ 7,412 α ³ - 13,97 α ⁴ - 2,435 h + 9,542 h ² - ^⎪ ⎩- 13,48 h ³ + 6,229 h ⁴ > 0;

условие устойчивости для треугольного крыла мало удлинения с углом поперечного V> 0 будет

⎧- 0, 029 9 + 0,125 h + 0, 001 66 α - _⎪ - 0,0146 α h - 0,2826 h ² + ^⎪ _⎪ + 0,0254 α h ² + 0,00111 α ² + ⎪+ 0, 000 72 α ² h + 0, 280 h ³ - ^⎪ ⎪- 0,003 21 α ² h ² - 0,011 α h ³ + ^⎨ ⎪+ 0,00138 α ² h ³ - 1,181 ⋅ 10 ^{- 4} α ³ + ^⎪ _⎪ + 1,732 ⋅ 10 ^{- 4} α ³ h - 0,102 h ⁴ < 0, ⎪ _⎪ 0, 212 + 0,678 97 α - 13,0311 α ² + ⎪+ 117,41 α ³ - 382,91 α ⁴ - 1,972 5 h + ^⎪ ⎩+ 7,54 h ² - 10,55 h ³ - 4,856 h ⁴ > 0.

К >

------о

Л

ji

О 0,5       1        1,5

Л

в

Рис. 5. Относительная координата аэродинамического фокуса: а - а = 2 град.; б - а = 4 град.; в - а = 7 град.

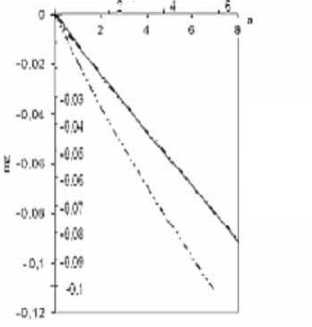
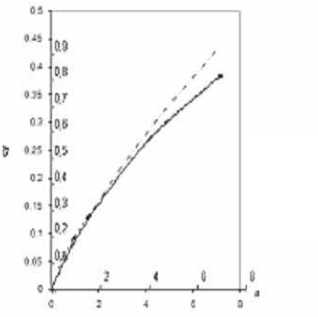
Рис. 6. Численные результаты решения линейной стационарной задачи безотрывного обтекания треугольного крыла малого удлинения с углом поперечного V> 0 вблизи экрана без шайб и с шайбами высотой 0,086 _б

Решая данные системы нелинейных неравенств, можно определить диапазон углов атаки и относительных высот движения, в которых крыло обладает статической устойчивостью, а следовательно, обеспечена безопасная эксплуатация аппарата.

Таким образом, решены линейные стационарные задачи безотрывного обтекания для прямоугольного крыла, треугольного крыла с углом поперечного V> 0 и V< О, получены численные значения аэродинамических коэффициентов cy (а, Л) и mz (а, Л), относительной координаты аэродинамического фокусах(а, Л). Построены функциональные зависимости c=_/(a, Л), mz =у(а, Л), х=/(а, Л). Используя критерии Иродова, для оценки устойчивости несущей поверхности вблизи экрана получены многочлены, позволяющие определить диапазон углов атаки и относительных высот движения. Кроме этого, сделаны выводы, что для крыльев треугольной формы с углами поперечного V< 0 или V> 0 наблюдается меньшее смещение аэродинамического фокуса при изменении высоты движения, однако отсутствие шайб на крыльях с углом поперечного V> 0 приводит к их худшей несущей способности.