Анализ осевого распределения, формируемого фраксиконом в параксиальном и непараксиальном случаях

Сочетание аксикона с линзой, называемое иногда линзаконом [1], позволяет управлять как продольным, так и поперечным распределением лазерных пучков [1-5].

Под аксиконом [6] понимается любой оптический элемент, обладающий осевой симметрией, который за счет отражения и/или преломления преобразует свет от точечного источника, расположенного на оптической оси, в осевой отрезок. В этом состоит отличие аксикона от линзы, которая изображает точечный источник в точку, и его преимущество. К сожалению, это преимущество аксикона сопровождается низким качеством изображения при использовании его как отдельного изображающего элемента [7, 8]. Также другое преимущество аксикона - изображение точки с меньшим поперечным дифракционным пределом (меньшим расплыванием) – имеет своим продолжением в качестве недостатка более высокий уровень боковых лепестков, что также препятствует получению качественного изображения.

В работе [4] было показано, что при использовании средств дифракционной оптики тандем линза+аксикон можно заменить одним дифрак-

ционным элементом (названным фраксиконом), фаза которого имеет дробную степень зависимости от радиальной координаты. В этой же работе было показано, что за счет вариации параметров можно получить аналог не только линзакона, но и логарифмического аксикона, но без сингулярности в центральной части оптического элемента.

Рефракционные аналоги таких элементов исследовались в работе [9] в рамках геометрооптической модели. Оптический элемент назван обобщенной линзой, так как при конкретных параметрах он сводится к классическим элементам, таким как параболическая линза или аксикон. Однако вариации параметров позволяют получать в одном элементе комбинированные свойства набора из двух и более оптических элементов.

Исследование фокусирующих свойств обобщенной линзы по сравнению с классическими оптическими элементами является актуальными для многих приложений, так как позволит заменить набор оптических элементов одним дифракционным элементом.

В данной работе на основе метода стационарной фазы получены аналитические выражения для осевого распределения, формируемого фраксиконом в параксиальном приближении. Также выполнено численное моделирование действия фраксикона как в параксиальном, так и непараксиальном случаях с использованием метода разложения по плоским волнам. Определены границы корректности полученных аналитических выражений в зависимости от параметров оптического элемента, включая его числовую апертуру.

1. ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

Рассмотрим радиально-симметричный дифракционный оптический элемент, фаза которого имеет дробную степень зависимости от радиальной координаты – фраксикон:

т ( r ) = exp [- i ( k a ₀ r )^y ] , r <  R , (1) где k = 2 п I Л , a ₀ - безразмерный коэффициент, связанный с числовой апертурой оптического элемента и определяющий степень фокусировки.

Дифракция плоской волны на оптическом элементе (1) в параксиальном случае вычисляется по формуле:

Имеем две стационарные точки:

r ₁ = 0,

r ₂

( k ^Y ) y -2

( Y z ^ Q J

.

Точка перегиба:

r p

(      k ^{1 - Y}

A Y -2

( Y ⁽ Y ^- 1) ^{z a} > J

.

Значения в стационарных точках:

f ( r 1 ) = 0, f -'( r i ) =+» ;

U ( p , z ) = k exp ikz +

ik p ² 2 z

I-1-Y -2 p-Y                 (v-TxlH f (r) =       I 12-11, f'(r) =(Y 2)k . (7)

2             Y            Y                 2              Y

( Y z O > J 2 z a Y V у J           z a Y

R xj t( r)exp

x ikr2 2z

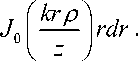
На оптической оси формула (2) примет вид:

R

U ( p = 0, z ) = — exp zkz )jexp - ( k a r ) ^Y + ^ r- rdr (3)

iz

. 2

Для вычисления интеграла в формуле (3) воспользуемся методом стационарной фазы (МСФ) [10]. Этот метод основан на том, что при быстро осциллирующей подынтегральной функции главный вклад дают окрестности точек, в которых частота (производная от фазы) равна нулю. Поэтому выполним разложение фазовой функции в (3) в ряд Тейлора и запишем приближённое равенство:

^ex P ⁽ if ^{( r} ) ) « ^eX P ^{( i [ f (} r e ) ⁺ f 4 ^r 0^{)( r} — ^r 0^{) 2 I2} ] ⁾ , ^(4а) в котором точка r ₀ определяется из условия:

f ' ( r 0 ) = 0 ,               (4б)

Если стационарных точек несколько, то производится разбиение отрезка интегрирования.

В классическом МСФ остальные множители в подынтегральной функции заменяются значениями при подстановке r = r ₀ , а пределы интегрирования расширяются до бесконечных. Естественно, предполагается, что стационарная точка лежит внутри отрезка интегрирования и не очень близко к его концу. Если она совпадает с концом отрезка, то соответствующий ей предел интегрирования заменяется нулём (а не бесконечностью).

В нашем случае надо проанализировать функцию:

Классический метод стационарной фазы в данной ситуации применим только во второй стационарной точке. Первая стационарная точка (нуль) (даже если мы не подставим r = r ₀ = 0 в нефазовый множитель, что дало бы в ответе нуль) не может быть использована - из-за бесконечности второй производной.

Поэтому нам придётся отказаться от применения классического МСФ и действовать следующим образом. Разделим отрезок интегрирования в точке перегиба (6). Тогда общая амплитуда равна сумме:

U ( z ) = U i ( z ) + U 2 ( z ) .

Естественно, что второй отрезок существует только при R >  r_p .

Интеграл по первому интервалу |^ 0, ^rp ] ^вычисляется без разложения фазовой функции в ряд Тейлора. Само использование ряда Тейлора сводится к обрыванию ряда на слагаемом второй степени. Например, при у >  2 в нулевой стационарной точке можно отбросить слагаемое r ^Y , имеющее более высокий порядок малости. Здесь по

k2 r^ 2 z a >

Такой способ имеет два недостатка. Один состоит в том, что результат выражается через специальные функции, для которых нет легко доступных таблиц. Второй заключается в том факте, что при некоторых значениях параметра g и k1-> величины , пренебрежение слагаемым 2 za> ,

аналогии мы могли бы отбросить слагаемое

f ( r )

= r ^Y

k ^{1 - Y}

r

2 z a >

k ^{1 - Y} r ²

может стать некорректным. Воспользу- 2 z a >

в диапазоне 1 < у <  2 .

емся эмпирическим приёмом, позволяющим избавиться от обеих проблем.

Обоснованием этого приема является вид графика функции r3/2 - r2 (частный пример общей формулы) на участке её неотрицательности. Так как особенность у второй производной (в отличие от особенности первой производной и тем более самой функции) визуально никак не проявляется, то на участке L0, rp J функцию к 1-уг 2

rY--можно приблизить функцией в'2, 2 zaY после чего интеграл (3) легко вычисляется:

U 1 ( P = 0, z ) =

много меньше. В частном примере r ^3/2 - r ² оно становится меньше только в д/ 1.8 « 1.34 раза.

3) Взвешенный метод наименьших квадратов.

Так как осцилляции увеличиваются с ростом r , нам важнее приблизить функцию вблизи нуля, поэтому весовую функцию возьмём убывающей. Если выбрать линейный вес, то находим мини-

мум интеграла

r p Г

j rY

к ^{1 - Y} r ²

2 z a Y

- p r ²

1 -

V

r

= — I" exp - i ( ka ₀) z

Y

к 1 " ^Y r ²

2 za 0 Y

r _p

— j exp |- i ( ka ₀ ) ^Y в' ² J rdr = z ₀

^ik Y ( Г V 7 Vo 2 1 ------{expl-p a   в'„ г 2 z a ^YyP {    ^{L ( 0} ) ^Hp J

rdr

Далее оценим параметр в . Приближение можно делать разными способами, приведём три из них.

1) Метод коллокации.

Приравниваем значения функций на концах отрезка.

Равенство на левом конце выполняется само по себе, а на правом даёт уравнение

r

-

2 z a_n ^Y

rrp решая которое, найдём:

в =

к ^{1 - Y} Г

= в ' ,

^{2 z aY} V Y ( Y ^- 1)

- 1

.

(9а)

Выражение получается простым, но можно доказать, что такое приближение будет с недостатком на всём отрезке.

2) Метод наименьших квадратов.

Находим минимум интеграла

r p Г

[ rY

к ^{1 - Y} r ²

2 zaY

pr2

dr

,

который достигается при значении

в =

к ^{1 - Y} Г

-

Л

^{2 z aY} I ⁽ Y + ³⁾ Y ⁽ Y ^- 1)

¹ (9б)

Отметим для полноты, что среднеквадратич-

ное отклонение не обязательно становится на-

^r dr

г

' p 7

который достигается при значении

TO L Г 601 ) ^{2 z a} 0 ^Y V ⁽ Y + ⁴⁾⁽ Y + ³⁾ Y ⁽ Y ^- 1) 7

. (9в)

Во всех случаях имеет место равенство вида

в =

к ^{1 - Y} ---P

2 z a Y .

Тогда с учётом (6) равенство (8) примет вид

i Г к

U X p = 0, z ) =—l exp - ip—r p\ L 2 z

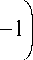
i

P

exp

^-2 ^{i p} ( ^a 0 ^Y ( Y ( Y ^- 1) ) ( ^kz ) ^Y ) ^{Y -} 1>

Если окажется, что R <  r_p , то можно применить (8)-(10) с заменой верхнего предела:

U 1⁽ p = 0, z ) = — | exp ^- i p ^-R² p V L 2 z

^- 1 1 . (10а)

Но более точным (так как отрезок интегрирования стал короче) будет применить (8) с другим значением в , полученным тем же способом, что и в (9), но на основе другого отрезка.

По методу коллокации получается

к1-Y в = RY-2--—-, а по МНК 2za0Y

в =— R ^{Y - 2}

Y + 3

к ^1-Y

2 za Y

(взвешенный МНК в таком виде не рассмотрен, но вид будет аналогичным).

Отметим, что полученные выражения для в

к ^{1 -} Y

Y -2

имеют вид в = pR--

2 z a ₀ ^Y

Подставив в (8) значение в , получим, что при ^R <  r p :

^{1 -} y

U 1 ( P = 0, z ) = -----7------------ Y ^ X

Y I t n y - 2        ^к I

2 z a Y P R ^Y

0     '                                 Y

V               2 z a 0 7

x l exp

- i p ( k a ₀ R ) ^Y I exp

i^k R ² 2 z

, (10б)

- 1

1, метод коллокации;

где p = ^ 5

у + 3

, МНК.

Так как r = [ya ⁷ zk ^{7 1} ) 1/⁽2 ⁷) и r p = r ₀ ( У — 1 )^{№ Y} ) увеличиваются с ростом z , то в какой-то момент U 2 ( p = 0, z ) исчезнет, и поведение амплитуды при большом z будет определяться только предельным значением U 1 ( p = 0, z ) . Ограничиваясь первым порядком малости, получим, что при использовании приближения (10а)

k 2

амплитуда убывает как R , а при (10б)

—i .1—г" Г exp (-ip (kaR -1 PR-2 2a-Jy-1 z L P( ( 0 ) ) J .

Хотя в обоих случаях амплитуда стремится к нулю как 1 / z (что, очевидно, и должно быть), но приближение (10б) явно показывает интуитивно ожидаемый из (3) вид спадения амплитуды.

Интеграл по второму интервалу [ r p , R J (если он есть) после применения разложения (4а) вычисляется по модифицированному МСФ [11] с учётом того, что разность у — 2 отрицательна для 1 < у <  2 . В этом случае получаем:

Амплитуда U 1 ( p = 0, z ) и первое слагаемое в U ₂ ( p = 0, z ) сравнительно невелики, и поэтому играют малую роль в области с большими значениями амплитуды, т.е. на значительном расстоянии от оптического элемента. Поэтому для упрощения анализа распределения интенсивности ограничимся только вторым слагаемым в (11), причём предположим, что функции Френеля можно заменить их предельными значениями. То есть, мы находимся в условиях, когда для интеграла по интервалу | r p , R применим классический МСФ.

Если требуемые условия выполнены, то интенсивность равна:

I ^{( z} ) ^м Т² ^ ( y ^2a 2^Y ( ^kz )⁷ ) ^2—7 . (12) 2 — 7 '

Максимальную интенсивность можно найти из условия, что стационарная точка лежит немного левее края отрезка интегрирования [11]. Предположим, что r ₀ = R , тогда:

R2—— kk——1aY ’

\ 2яу , _dV ⁽¹³⁾ I ( z = z max ) = ----- ( ^{k a} 0 ^R ) .

2 — у

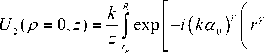
k ^{| —} r 2 ² У

^{2 z a}o У

—i — exp ^|— i ( k a ,) ⁷ f ( г ,) ! x У — 2 L                   -I

rdr м

x

^exP У ⁽ Y ^{— 2)( R — r} 0 ) 2

^— exP¹ — ⁽ Y ^{— 2)( r} 0 ^— r p ^{) 2} L 2 z

₊ y ^_r ^l/(2—* )

^{2 —} Y

г

^— i ( ^{k a} 0 ) f ( ^r 0 ) J' ( ^kz ) ^2(2—T ) ^x

x

C (k- (2 — у )( R — r ₀) ² ) + C ( P (2 — у )( r — r_p ) ² ) + V 2 z                у V 2 z                у

+ iS ^f k (2 — у )( R — r ₀ ) ² ) + iS ^f ; (2 — у )( r — r_p ) ² ) V 2 z                   У V 2 z                   У

Здесь

_x 1 x cos ( t ) ,       22 x?     / 2 \ ,

C ( x ) = ,— J — dt-=dt = J — j cos ( t ²) dt

P2n ^J₀ V t          П Tt 0₀      ' '

и S ( x ) =

функции Френеля. Для краткости мы не стали везде подставлять значения из (5)-(7), под r ₀ понимается вторая стационарная точка из (5). В (11) предполагается,что R >  r ₀ . Если r p <  R <  r ₀ , то во втором слагаемом у членов с R в аргументе знак меняется на противоположный.

На самом деле, это значение с избытком: несколько меньшее значение, чем (13), достигается при z <  z _max . А в самой точке z _max интенсивность будет в четыре раза меньше, чем по формуле (13).

Найдём теперь максимальную достижимую интенсивность в этой точке. Хотя формулы похожи на выражения, полученные для аксикона [11] (при подстановке у = 1 они совпадут, то есть имеет место непрерывный переход), сейчас ситуация больше напоминает линзу, так как тоже существует максимальный радиус оптического элемента. Поэтому мы не можем одновременно увеличивать а ₀ и R .

Рассуждая как в случае с линзой [11], проанализируем функцию sin( k a ₀ r )⁷ и найдём, когда мгновенный полупериод фазовой функции будет не меньше половины длины волны. Полупериодом будем считать расстояние между соседними нулями этой функции.

Нули находятся в точках:

r = ⁽ m K ^{) 1Z 7}

^m k a ₀ ’

расстояние между соседними нулями равно:

Y rm+1 — rm =     ((m + 1)17 7 — m 17 )

k a ₀

и убывает с ростом номера m . Из условия, что

это расстояние не меньше половины длины волны, получим неравенство:

( m + 1)¹ / ^Y - m ^{17 Y} >  а ₀ П ^{17 Y} .

Обычно a0 мало, поэтому вблизи равенства номер велик, и левую часть можно приближённо заменить на —1-17— . Получаем, что максималь-

Y m ⁷

но возможный номер m равен:

п(уа0)Y/(Y-1) ’ а соответствующий максимальный радиус:

R

max

Y^1/( Y ^{- 1)} ка ^/( Y ^{- 1)} .

Подставив (14) в (13), получим максимально возможную интенсивность на краю фокального отрезка при заданной длине волны:

I

max

2 л

Г

х 1/( y -1)

2 - y ( Y^ )

Это значение не зависит от длины волны. При Y ^ 2 слагаемое U ₂ ( р = 0, z ) исчезает, поэтому бесконечной интенсивности не будет, кроме того, у линзы принципиально другой вид распределения интенсивности, не похожий на (12). При Y ^ 1 получим, что при а ₀ <  1 интенсивность может стать сколь угодно большой, что очевидно, так как аксикон не имеет предельного радиуса, иначе получится нуль, так как аксикон не пропускает излучения.

Отметим также, что если функции Френеля не заменять предельными значениями, то можно доказать [11], что максимальная интенсивность будет примерно в 1,37 раза больше, чем по (13).

Сравним с результатами, полученными в геометрооптическом приближении [9]. Чтобы это сделать, сначала найдём связь между параметрами, описывающими элемент. Для этого приравняем набег фазы в геометрооптическом варианте k ( n - 1) a g r ^Y к набегу фазы из (1) ( k a ₀ ) ^Y r ^Y . Получаем соотношение:

a g

k ^Y а

( n - 1) .

Теперь сравним распределение интенсивности. При геометрооптическом подходе распреде- ление интенсивности в параксиальной области описывается в работе [9] формулой:

2 na ( n - 1)_r

; =--------- Г a (n -1)z 12-y g     2(2 - y ) L g J .

Если в (17) подставить (16), и сравнить с (12), то получим, что распределения совпадают с точностью до множителя 2п : результат подстановки в 2п раз меньше выражения (12).

Сравнение для максимальной интенсивности выполнить невозможно, так как в геометрооптическом подходе максимум достигается за пределами области применимости формулы (17), при этом он не соответствует максимальному радиусу оптического элемента, в отличие от (13). Однако в [9] было аналитически получено значение фокусного расстояния. Для общности приведём эти значения. Максимальный радиус при геометрооптическом подходе с учётом (16) определяется равенством g J n - 1 ^ 2 Y-2 1

^max = I n + 1 ) Y^{KY - 1)} k a Y ^{( Y - 1)} . ⁽¹⁸⁾

Оно отличается от (14) первым множителем, меньшим единицы. Максимальной интенсивности, причём аналитически равной бесконечности (поэтому и употреблено слово фокусный), соответствует радиус:

R f = r m ,x ( 2 - y Г ^Y - ^2| . (19)

Второй множитель здесь меньше единицы. Используя формулу для мгновенного фокуса из [9], находим фокусное расстояние

= n Yr-i + 2 - 2/ Y _R 2-y =

Y ( n ² - 1) a g      ^f

( n V / - 1 + 2 - 2/ y ) (2 - Y )^{( Y№Y} ) ( _{n - 1}) 1/< y - 1)

« 0 =

y ( kR ) ^Y -1

NA

1/ y

где R – радиус оптического элемента, NA – числовая апертура.

Помимо данной методики в работе использовались ещё две: численное интегрирование по формуле (2) и расчёт с в непараксиальном приближении через разложение по плоским волнам, который производился по следующей формуле:

^to 0                           .           ,_______________.

E ( p , z ) = k ² j P ( to )exp ( ikz Vl- ^ ²) J 0 ( top ) todto, (22)

R где P(to) = j т (r ) J0 (ktor)rdr — простран-0

ственный спектр, to ₀ - радиус учитываемых пространственных частот.

Для каждого из приведённых случаев производилось три вычисления среднеквадратичного отклонения d:

. S ap - между результатами расчёта по формулам (10), (10б), (11) и параксиальным численным интегрированием (2).

• .    S an — между результатами расчёта по формулам (10), (10б), (11) и непараксиальным расчетом через разложение по плоским волнам (22);

• .    S pn - между результатами расчёта в параксиальном (2) и непараксиальном случае (22);

На рис. 1-3 приведены результаты численно- го моделирования распределения формируемой интенсивности для элементов с числовыми апертурами NA=0,1, NA=0,5 и NA=0,9. В расчетах были выбраны значения g=1,1; g=1,5; g=1,9, которые соответствуют середине и краям диапазона 1 < y < 2 .

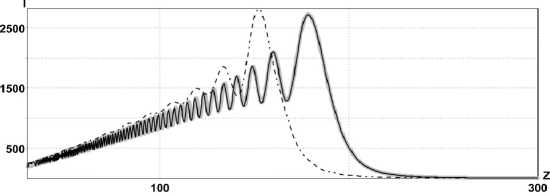
На всех рисунках тип линий имеет следующее соответствие: сплошная чёрная линия – результаты расчета по аналитическим формулам (10), (10б), (11); серая линия – расчёт в параксиальном приближении численным интегрированием (2); пунктирная линия – расчёт в непараксиальном случае через разложение по плоским волнам (22).

По результатам, приведенным на рис. 1, видно, что при низкой числовой апертуре параксиальная и непараксиальная модели расчетов дают близкий результат.

Аналитические формулы (10), (10б), (11) согласуются с этими результатами при у <  1,5 . При Y ^ 2 наблюдается существенное отличие от численных результатов. Это связано с тем фактом, что полученные выражения имеют непрерывный переход к Y =1, при котором модифицированный МСФ [11] даёт точное решение. В то же время при у ^ 2 непрерывного перехода к Y =2 (для которого также есть точное решение) быть не может, что очевидно из полученных формул, в которых имеется величина 2 — y в знаменателе.

Замети также, что все три использованных метода расчёта показали очень близкие (отклонение менее 2%) значения интенсивности для глав- в)

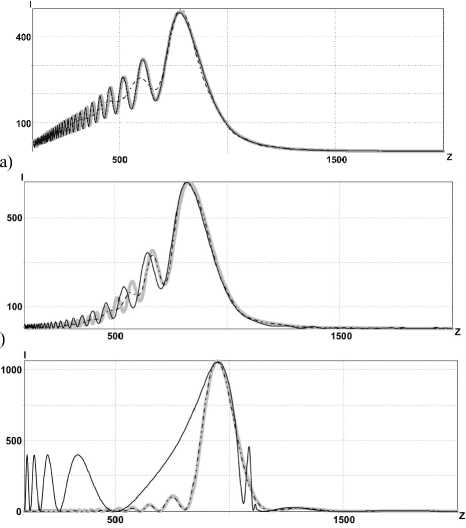
Рис. 1. Распределение интенсивности на оптической оси для фраксикона с NA=0,1:

(а) Y =1,1; « 0 = 0,0629; S a = 0,0733 , S an = 0,1142 , S pn = 0,1115 ;

(б) Y =1,5; « 0 = 0,0192; S ap = 0,0733 , S an = 0,072 , S pn = 0,0589 ;

(в) Y =1,9; О , = 0,01; S ap = 0,3 865 , S an = 0,4082 , S pn = 0,0111 .

а)

в)

б)

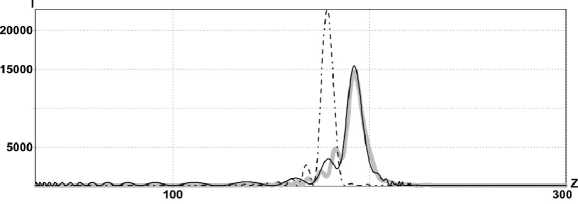
Рис. 2. Распределение интенсивности на оптической оси для для фраксикона с NA=0,5:

(а) γ =1,1; α 0 = 0, 2718; δ ap = 0,0479 , δ an = 0,1282 , δ pn = 0,1264 ;

(б) γ =1,5; α 0 = 0, 0561; δ ap = 0,0722 , δ an = 0,1279 , δ pn = 0,1433 ;

(в) γ =1,9; α 0 = 0, 023; δ ap = 0,1642 , δ an = 0,1685 , δ pn = 0,231 .

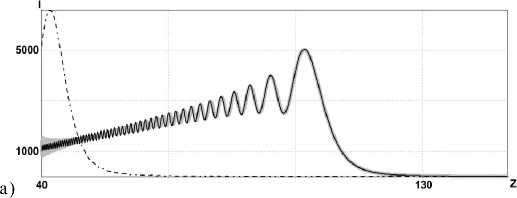
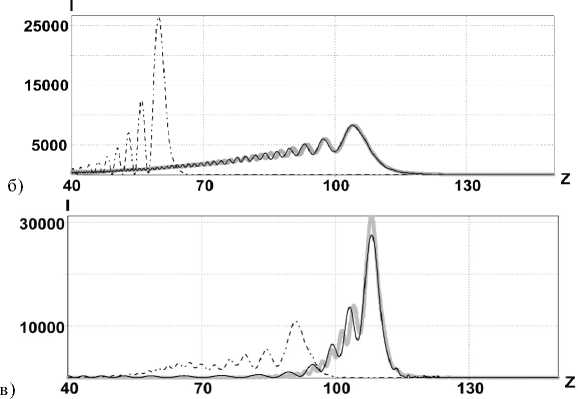
Рис. 3. Распределение интенсивности на оптической оси для фраксикона с NA=0,9:

(а) γ =1,1; α 0 = 0, 4639; δ ap = 0,0427 , δ an = 0,5008 , δ pn = 0,4997 ;

(б) γ =1,5; α 0 = 0, 0831; δ ap = 0,0605 , δ an = 0,4442 , δ pn = 0,443 ;

(в) γ =1,9; α 0 = 0, 0319; δ ap = 0,127 , δ an = 0,3259 , δ pn = 0,3027 .

ного пика и его положения на оптической оси.

Для средних значений числовой апертуры имеется стабильное различие (12-20%) между результатами, полученными в параксиальном и непараксиальном случаях. При этом аналитические формулы показывают хорошее согласование с параксиальной моделью, в рамках которой формулы и были получены. Причем даже при γ → 2

погрешность хоть и растет, но имеет значительно меньший уровень, чем в предыдущем случае для низких значнений числовой апертуры.

Заметим также, что при γ → 2 сближаются оценки для положения главного максимума, рассчитанного в параксиальном и непараксиальном случаях.

Для высоких значений числовой апертуры различие между параксиальным и непараксиальном расчетом предсказуемо высокое, хотя с ростом γ оно несколько уменьшается.

Аналитические выражения показывают хорошее согласование с параксиальной моделью и могут быть использованы вместо численных расчетов, особенно в ближней зоне дифракции, где возможны большие погрешности численного расчета.

ЗАКЛЮЧЕНИЕ

В работе рассмотрено действие фраксикона, представляющего собой обобщенный дифракционный оптический элемент, частными случаями которого являются параболическая линза и ак-сикон. Получены аналитические выражения для распределения комплексной амплитуды и интенсивности вдоль оптической оси в рамках скалярной параксиальной волновой модели.

Также проведено численное моделирование с использованием операторов распространения в свободном пространстве в параксиальном и непараксиальном случае.

Показано, что аналитические выражения очень хорошо аппроксимируют параксиальное решение при γ ≤ 1, 5 , причем погрешность уменьшается при увеличении значения числовой апертуры оптического элемента. Таким образом, они могут быть использованы вместо численных расчетов, особенно в ближней зоне дифракции, где возможны большие погрешности численного расчета.

Работа выполнена при финансовой поддержке ФЦП “Научные и научно-педагогические кадры инновационной России” (соглашение №8231), гранта РФФИ 13-07-97004-р_поволжье_а и гранта Президента РФ поддержки ведущих научных школ НШ-4128.2012.9.