Анализ осевого распределения при острой фокусировке для различных поляризаций освещающего пучка

Возможность управления продольным распределением является одной из составляющих решения задачи трёхмерного формирования светового излучения. Такая возможность особенно востребована в приложениях, где важно объёмное фокальное распределение – оптический захват и манипулирование, конфокальная и многофотонная микроскопия, оптическая литография, оптическое хранение данных, голография, прямая лазерная запись.

Известно, что использование узкой кольцевой диафрагмы, позволяющей уменьшить размер фокального пятна в поперечном направлении для излучения с радиальной поляризацией [1, 2], приводит к удлинению фокального пятна в продольном направлении. Таким образом, формируется тонкая световая игла [3]. Аналогичный результат, но при меньших потерях энергии, можно получить для полной апертуры за счёт использования дополнительных фазовых бинарных оптических элементов [4–6]. В случае азимутальной поляризации будет формироваться тонкая световая трубка [7, 8].

Однако часто необходимо также уменьшение размера фокального пятна вдоль оптической оси. Для этого используются различные методы, в том числе интерференция встречных пучков – так называемая 4pi-система [9, 10]. В работах [11, 12] был рассмотрен расчёт фазовых оптических элементов для достижения сверхразрешения в 4pi-системе в поперечном или продольном направлении. В работе [12] рассмотрен только случай линейной поляризации. Причём получены лишь приближённые аналитические оценки.

Также для линейной поляризации была решена обратная задача формирования осевого распределения на основе разложения ядра интегрального оператора по полиномам Гегенбауэра [13, 14].

Для цилиндрических пучков с азимутальной и радиальной поляризацией также были разработаны методы формирования заданного объёмного распределения [15–22], в том числе оптические «бутылки», полые световые сферы, цепочки и массивы фокальных пятен. Причём, учитывая сложность юстировки в 4pi-системе, рассматривался и расчёт фильтров для одной линзы [15, 17, 18]. Как правило, эти методы являются численными и часто итерационными.

Для различных целей и задач являются оптимальными те или иные типы поляризации, поэтому для выполнения сравнительной оценки полезно иметь аналитические оценки для наиболее часто используемых типов поляризации. В работе [23] были получены такие оценки для поперечного распределения в фокальной плоскости. В данной работе рассматривается аналитическое решение для осевого распределения при фокусировке излучения, ограниченного кольцевой апертурой произвольной ширины. Эти результаты могут быть использованы для оценки продольного распределения при фокусировке полей от различных колец, имеющих определённые значения фазы [12, 15]. Рассмотрены основные типы поляризации лазерного излучения – азимутальная, радиальная, круговая и линейная – как в случае плоского фазового фронта, так и при наличии вихревой фазы.

1. Анализ осевого распределения при различных поляризациях

Векторное электрическое поле в однородной диэлектрической среде вблизи фокуса, расположенного от объектива на расстоянии значительно большем длины волны, можно описать в приближении Дебая [24]:

E ( ρ , ϕ , z ) =- ^{if Θ 2 π} B ( θ , φ ) T ( θ ) P ( θ , φ ) × λ 0 0                                   (1)

×exp[ik(ρsinθcos(φ-ϕ)+zcosθ)]sinθdθdφ, где (θ, φ) – сферические угловые координаты выходного зрачка, B(θ, φ) – функция пропускания, T(θ) – функция аподизации зрачка; P(θ, φ) – матрица поляризации, которая определяется по коэффициентам поляризации падающего пучка, nsinΘ = NA , n – показа- тель преломления среды, NA – числовая апертура линзы, f – фокусное расстояние. В апланатической системе пересчёт для радиальной координаты выполняется по синусному правилу r = f sin 6 и функция аподизации зрачка полагается равной T(6) = Vcos 6 .

Для функции пропускания, представимой в виде суперпозиции:

B ^{( 6 , ф )} = Е c m^Dm ^{( 6 )}e^XP ( im ^Ф) ,                  ⁽²⁾

m интеграл по ф в (1) будет выражаться через соответствующую сумму функций Бесселя первого рода различного порядка, а векторное электрическое поле в фокальной области вычисляется одномерным интегрированием [25]:

^E m ( Р , Ф , z ) = — ^ik f Е i m c m exP⁽ im Ф ) ^X m

0                     _____ xjDm (6)Qm (Р,Ф,6) VCosO sin6X              (3)

x exp ( ikz cos 6 ) d 6 ,

Q mx ’ ^d ( р , Ф , 6 ) =

J m ( t ) + 4 [ 2 J m ( t ) — e i ^{2 Ф} J m + 2 < t ) —

- e ^- i ^{2 ф} J m - 2 ( t ) ] (cos 6- 1)

= 4 [ e i ^{2 ф} J m + 2 ( t ) - e " i ^{2 ф} J m - 2 ( t ) ] (cos 6- 1)

- 2 [ e i ^Ф J m + 1 ( t ) - e " i ^ф J m - 1 ( t ) ] sin 6

где t = k р sin 6 .

Рассмотрим поле (3) на оптической оси для равномерной пропускающей функции в кольце с радиусами 6 ₁ и 6 ₂ :

^Dm (⁶) =

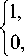
6 1 <6<6 2 , иначе.

^E m ( ⁰, Ф , z ) = ^{- ikf} Е i m c m exP⁽ im Ф ) ^X

m

где D m ( 6 ) может быть любой одномерной функцией, в том числе радиальной частью мод Гаусса–Ла-герра, Цернике, Бесселя и т.д., а вид Q _m ( р , ф , 6 ) зависит от поляризации входного поля. В частности, для декартовых компонент:

– при азимутальной поляризации:

«2                    ._______ (9)

x j Q _m ( 0, Ф , 6 ) Vcos 6 sin 6 exp ( ikz cos 6 ) d 6 .

Выражения (4)–(7) значительно упрощаются при р = 0 и имеют ненулевое значение только для нескольких значений вихревого порядка m [25]:

Q m • d ( р , ф , 6 ) = 2

■ - [ ё ^ф J m _{+ l}( t ) + e " i ^ф J m _ , ( t ) ] i [ ё ^ф J m + 1 ( t ) - e -^Ф J m - 1 ( t ) ] 0

Q OzLd1 (0, Ф , 6 ) = 2 e ^ф i ^Ф

– при радиальной поляризации:

q rad • d ( р , ф , 6 ) =

	■ i [ e i Ф J m + 1 ( t ) - e - i Ф J m - 1 ( t ) ] cos 6"
= 1 2	[ e i Ф J m + 1 ( t ) + e - i Ф J m - 1 ( t ) ] cos 6	(5) ;
	- 2 J m ( t )sin 6

– при круговой поляризации (правой «+» и левой

« - »):

Q

circ ± , d

m

( р , Ф , 6 ) = — X

J m ( t ) + 2 [ J m ( t ) — e ± i 2 ^Ф J m ± 2 ( t ) ] (cos 6 — 1)

± i { J m ( t ) + 2 ( J m ( t ) + e ± i 2 ^Ф J m ± 2 ( t ) ) (cOS 6 - 1) ^

+ ie ± i ^ф J_m ± 1 ( t )sin 6

– при линейной x -поляризации:

Q mad 0 d (0, Ф , 6 ) =     0

(6) ;

∓ i 0

- sin 6

Q ™-_'1d (0, Ф , 6 ) = 2 e ^ф i ^Ф

Q 2+d (0, Ф , 6 ) = ^22

Q circ + , d m =- 1

+ i cos 6 cos 6 0

1 + cos 6

i ( 1 + cos 6 )

(0, Ф , 6 ) =      e i ^Ф

- i sin 6

Qcirc+, d m=- 2

(0, Ф , 6 ) =       e

Q mm= 0 ^d (0, Ф , 6 ) = 2

i 2 ф

1 - cos 6

- i (1 - cos 6 )

1 + cos 6

(11а)

(11б)

(12а)

(12б)

(12в)

(13а)

Q m =± 1 (0, Ф , 6 ) = 2 e ⁴ i ^ф

q m: ± ¹ (о, ф , 6 ) = 4 e ^ф

± i sin 6

,

(13б)

1 - cos 6 ± i (1 - cos 6 ) 0

.

(13в)

Как видно из выражений (10)–(13), поле (9) сводится к сумме слагаемых вида:

G ( z ) = J ( cos 6 )¹² sin 6 exp ( ikz cos 6 ) d 6 ,     (14а)

_   ( cos 6j) 12 exp ( ikz cos 6j- ( cos6₂ ) 12

G ( z ) = V-----V ikz

G c ( z ) = J ( cos 6 )^{3 2} sin 6 exp ( ikz cos 6 ) d 6 ,     (146)

G s ( z ) = J ( cos 6 )^1/2 ( sin 6 )² exp ( ikz cos 6 ) d 6 . (14в) 6 1

Причём выражения G ( z ) и G_c ( z ) соответствуют поперечным компонентам, а G_s ( z ) – продольной компоненте. Выполним анализ выражений (14).

2. Аналитическая оценка продольных распределений

Интеграл (14а) вычисляется точно:

exp ( ikz cos 6 ₂ )

----^П' ^2 - { [ C ( k|z | cos 6 1 ) - C ( k|z | cos 6 2 ) ] + i sgn( z ) ^ S ( k|z | cos 6 1 ) - S ( k|z | cos 6 2 ) ] } , i ^{( k}\^z\ )

где C ( - ), S ( - ) - функции Френеля [26].

Интеграл (14б) выражается через (15):

G , x = ( cos 6 1 ) ³ 2 exp ( ikz cos 6 1 ) - ( cos 6 2 ) ³ 2 exp ( ikz cos 6 2 ) 3 g

c ^{( z} ) =                               ikz                                2 ikz ^{(z ).                                 (} )

Интеграл (14в) можно взять приближённо. Сделаем замену переменных:

Gs (z) = J (cos6)1'2 (sin6)2 exp (ikzcos6)d6 = cos 61          __________

J Vx 41 - x2 exp (ikzx) dx = cos 62

J cos 6 1

= J 2 y >] 1 - y ⁴ exp ( ikzy ² ) d y .

a] cos 0 2

В выражении (17) разложим квадратный корень в ряд Тейлора. При этом нулевое слагаемое ряда соответствует G ( z ) из (15). Заметим, что чем меньше 6 1 , тем медленнее сходится ряд. Поэтому если хотя бы один предел по углу попадает в параксиальную область, то стоит использовать какой-либо другой приближённый способ. Далее будем считать, что 6 1 достаточно велико, чтобы ограничиться двумя слагаемыми ряда. Тогда выражение (17) приближённо равно:

Г

G s ( z ) = G ( z ) 1 +

I

15       ( cos 6 1 ) ⁵ 2 exp ( ikz cos 6 1 ) - ( cos 6 2 ) ⁵ 2 exp ( ikz cos 6 2 )

8 ( kz ) ² _?                                 2 ikz

- 5

( cos 6 1 ) ³ 2 exp ( ikz cos 6 1 ) - ( cos 6 ₂ ) ³ 2 exp ( ikz cos 6 ₂ ) 4 ( kz ) 2

Полученные выражения являются довольно громоздкими и неудобными для анализа. Поэтому рассмотрим далее приближённые оценки.

Если z велико, то интенсивность для выражений (15), (16) и (18) примет следующий вид:

I     1₂ cos 6 + cos 6₂ - 2^1 cos 6 cos 6₂ cos [ kz (cos 6₂ - cos 9,) ^

G ( - ■)  ---------—177— -------•

⁽ kz )

.       .₂ cos³ 6j + cos³ 6₂ - 2a] cos³ 6j cos³ 6₂ cos ^ kz (cos 6₂ - cos 6J ]

G c ⁽ z )  -------------------'------TTv------- -------------- ,

^{( kz} )

I ^Gs ⁽ z )|²

cos 6 1 ( 2 - cos² 6 1 ) + cos 6 ₂ ( 2 - cos² 6 ₂ ) 4 ( kz ) 2

a^ cos 6 1 cos 6 ₂ ( 2 - cos² 6 1 )( 2 - cos² 6 ₂ ) cos ^ kz ( cos 6 ₂ - cos 6 1 ) ]

(19а)

(19б)

(19в)

Выражения (19) имеют примерно одинаковый осциллирующий характер, причём период осцилляций зависит от разности ( cos 6 1 - cos 6 2 ) . Если раз-

ность велика, то осцилляции чаще.

Оценка выражений (15), (16) и (18) при малых значениях z получается громоздкой, но также можно заметить аналогичную осциллирующую зависимость от ( cos 6 1 - cos 6 2 ) .

Более компактные оценки без зависимости от диапазона изменения z можно получить, когда в интегралах (14) отрезок интегрирования небольшой, т.е. кольцевая апертура не слишком широкая. В этом случае:

Gc (0) = J (cos 6)3/2 sin 6d6 = 61

= 5 [ ( ^{cos 6} i ) 52 ^-( ^{cos 6} 2 ) 52 ] ,

Gs (0) = J (cos 6)1'2 (sin 6)2 d6 =

= 5 [ ( cos 6 1 ) 32 sin 6 1 - ( cos 6 ₂ ) 32 sin 6 ₂ ] +

+ —

Ff 62 /?) f6 6 /?)

E --, n 2 - E —,N 2

( 2     )    (2    )

(23б)

(23в)

_____________62

G ( z ) = ^cos ( 6 a ) J sin 6 exp ( ikz cos 6 ) d 6 =

= Vcos (6a )G0 ( z ) ,

(20а)

Gc (z)- 7cos3 (6a)G0 (z),(206)

Gs ( z )” Vcos (6a ) sin (6a ) G0 ( z ) ,

G exp (ikz cos 61)-exp (ikz cos 62)

0                        ikz где 6a =(61 +62)/2.

Учитывая, что

, _и 4sin² l kz ( cos 6,- cos6, ) /2 I

I G d ( z )| =----- ^L *2 ------—,      (22)

(kz)

где E ( • ) - эллиптический интеграл второго рода [26].

В (23в) эллиптический интеграл находится в неканонической форме (модуль больше 1). Для удобства использования таблиц и стандартных подпрограмм выражение (23в) можно переписать в следующем виде:

G s ( 0 ) = 5 [ ( cos 6 1 ) 32 sin 6 1 - ( cos 6 ₂ ) 32 sin 6 ₂ ] +

- E

-

-

-

во всех случаях получается примерно одинаковая зависимость sin² ( o x ) / x ², период осцилляций которой определяется разностью ( cos 6 1 - cos 6 ₂ ) . Отличие состоит только в коэффициенте, который, в конечном счёте, будет определять вклад соответствующих компонент.

Из выражений (20) видно, что если кольцевая апертура пропускает центральные лучи, то коэффициент пропорциональности для G ( z ) и G_c ( z ) , соответствующих поперечным компонентам, будет значительно больше, чем коэффициент пропорциональности для G_s ( z ) , соответствующей продольной компоненте. Если же кольцевая апертура пропускает периферийные лучи, то G_s ( z ) будет близка по абсолютным значениям к G ( z ) .

Значения выражений (14) при z = 0 удобно получить, подставив z = 0 в соответствующие интегралы.

Таким образом, получим:

в ₂

G (0) = J (cos 6)^2 sin 6d6 =

= у [ ( cos ⁶ 1 ) ^{32 -}( cos ⁶ 2 ) ³² ] ,

(23а)

- F где F(•), E(•) - неполные эллиптические интегралы первого и второго рода [26].

• 3.    Численный анализ продольного распределения в зависимости от поляризации

• 3.1.    Азимутальная поляризация

Рассмотрим результаты моделирования при использовании выражения (9) для конкретных типов поляризации падающего излучения, содержащего суперпозицию вихревых фазовых функций.

Как следует из формул (9) и (10), при острой фокусировке азимутально-поляризованного излучения на оптической оси будут ненулевые значения только при наличии вихревой фазы первого порядка m = ± 1:

e az ( 0, _Ф , z ) = kL

С 1 ^- с - 1

- i (С1+ с-1)

G ( z ).

Из формулы (24) видно, что, меняя коэффициенты с1, с1, соответствующие вкладу вихревой фазы первого порядка с различными знаками, можно варьировать вклад x- и у-компонент. При с1 = с1 входное фа- зовое распределение будет соответствовать cos ф и на оси будет только у-компонента, а при c1 = -c-1 фазовое распределение на входе будет соответствовать sin ф и на оптической оси будет только x-компонента. Действие аналогичных бинарных фазовых структур на распределение в поперечной фокальной плоскости было рассмотрено в работе [6].

На рис. 1 показано осевое распределение общей нормированной интенсивности для азимутальной поляризации при с 1 = 1, c - 1 = 0 в (24) для кольцевой апертуры, ограниченной максимальным значением угла 0 2 = 82 ° и минимальным углом 0 1 = 0 ° (сплошная линия), 0 1 = 48 ° (штрихунктирная линия), 0 1 = 70 ° (пунктирная линия).

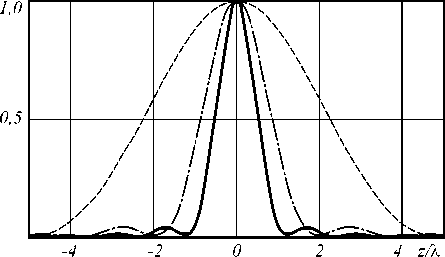
Рис. 1. Нормированное распределение общей интенсивности на оптической оси для азимутальной поляризации при m=1 при кольцевой апертуре, ограниченной углами 9 2 = 82 ° и 9 1 = 0 ° (сплошная линия), 9 1 = 48 ° (штрихпунктирная линия), 9 1 = 70 ° (пунктирная линия)

Как видно из рис. 1, интенсивность функции G ( z ) близка к sin² ( a x ) / x ², как предсказывалось в разделе 2. Причём от ширины кольцевой апертуры зависит период осцилляций, а следовательно, и глубина фокуса. Широкая кольцевая апертура позволяет сконцентрировать основную энергию около фокальной плоскости. Сужение кольцевой апертуры приводит к увеличению глубины фокуса, «растягиванию» энергии вдоль оптической оси.

• 3.2.    Радиальная поляризация

Из формул (9) и (11) следует, что при острой фокусировке радиально-поляризованного излучения на оптической оси будут ненулевые значения как в отсутствие вихревой фазы, так и при наличии вихревой фазы первого порядка:

e mad ( о, _Ф , z ) = f

^- i ( c l + С - 1 ) G c ⁽ z ) ( c l ^- c - 1 ) G c ⁽ z ) 2 ic 0 G s ( z )

Выражение (25) показывает, что распределение поперечных и продольной компонент имеет различный вид, причём вклад продольной компоненты даже при относительно небольшом значении c ₀ существенный.

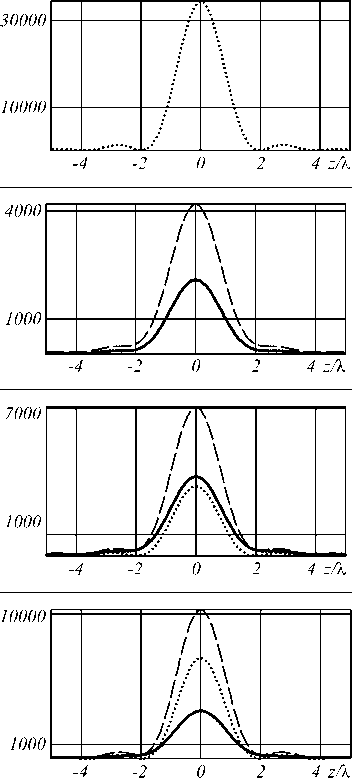
В табл. 1 приведены результаты моделирования острой фокусировки радиально-поляризованного излучения для кольцевой апертуры с 01 = 48° и 02 = 82° в случае различных значений коэффициентов c0, c1, c1, соответствующих суперпозиции вихревых фазовых функций в падающем пучке. При отсутствии вихревой фазы на оптической оси имеется только продольная компонента (первая строка табл. 1), а наличие вихревой фазы первого порядка любого знака приводит к появлению поперечных компонент (вторая строка табл. 1), причём нулевые значения Gs (z) практически совпадают с минимумами Gc (z) . Если используется суперпозиция (2) с различным соотношением весов | cm |2 , сумма которых нормирована, то при радиальной поляризации даже при относительно небольшом значении c0 вклад продольной компоненты на оси очень существенный (третья строка табл. 1). Заметим, что при равенстве c1 = c-1 суперпозиция (2) приводит к бинарной фазе входного распределения (четвёртая строка табл. 1).

• 3.3.    Круговая поляризация

Для излучения с круговой поляризацией (рассмотрим для определённости правую поляризацию) в выражении (9) используются формулы (12), из которых следует, что нужно учитывать суперпозицию вихревых фазовых функций вплоть до второго порядка:

E Т +(0, ф z ) = kf

^{iG (} z ) [ c 0 ^- c - 2 ] ^{+ iG}c ⁽ z ) [ ^c 0 ⁺ c - 2 ] ^- G ⁽ z ) [ c 0 + c - 2 ] ^- G c ⁽ z ) [ c 0 ^- c - 2 ]

2 ic - i G s ( z )

Из выражения (26) видно, что при c ₀ = ± c _{- 2} будут формироваться различные осевые распределения для x - и y -компонент. Наличие в падающем пучке вихревой фазовой функции первого порядка, направление вращения которой противоположно направлению круговой поляризации, приведёт к появлению на оптической оси продольной компоненты.

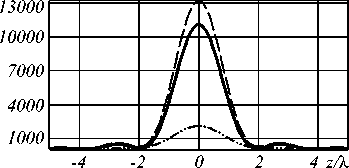
В табл. 2 приведены результаты моделирования острой фокусировки излучения с правой круговой поляризацией для кольцевой апертуры с 0 1 = 48 ° и 0 ₂ = 82 ° в случае различных значений коэффициентов c ₀, c 1 , c _{- 2}. При c ₀ = - c _{- 2} (первая строка табл. 2) распределение для x -компоненты соответствует G ( z ) , а для y -компоненты – G_c ( z ) , при этом хорошо видно, что интенсивность | G ( z ) |² значительно больше интенсивности | G_c ( z ) |² , как и следует из выражений (20). Заметим, что при круговой поляризации, хотя и можно добиться появления продольной компоненты на оптической оси за счёт вихревой фазы первого порядка (вторая строка табл. 2), вклад её сравним с вкладом поперечных компонент при соответствующем соотношении весов | c_m |² (третья строка табл. 2).

Таблица 1. Результаты моделирования фокусировки радиально-поляризованного излучения для кольцевой апертуры с 9 1 =48 ° и 9 2 =82 ° (интенсивность поперечных компонент - сплошная линия, z-компоненты – точечная линия, общей – пунктирная линия)

Входное распределение: амплитуда (негативное изображение) и фаза

Интенсивность на оптической оси cо = 1, c = c-j = 0

^c о = ⁰, c i = 1, c - 1 = ⁰

c ₀ = 0,31, c 1 = 0, c - 1 = 0,95

c ₀ = 0,45, c 1 = c - 1 = 0,63

• 3.4.    Линейная поляризация

Для излучения с линейной поляризацией (рассмотрим для определённости x -поляризацию) в выражении (9) используются формулы (13), из которых следует, что нужно учитывать суперпозицию вихревых фазовых функций вплоть до второго порядка:

e ^ ( 0, ф , z ) = f x

x

- 2 ic 0 [ G ( z ) + G c ( z ) ] + i ( c ₂ + c — 2 ) [ G ( z ) - G c ( z ) ]

^-( c 2 ^- c - 2 )[ G ^{( z} ) ^- G c ^{( z} ) ]

² i ( c i + c - i ) G s ^{( z} )

Как видно из выражения (27), используя различные суперпозиции вихревых функций, можно управлять вкладом различных компонент на оптической оси. При c1 = ±c-1 и c2 = ±c-2 будут иметь ме- сто бинарные фазовые структуры, действие которых на распределение в поперечной фокальной плоскости было рассмотрено в работе [6].

В табл. 3 приведены результаты моделирования острой фокусировки излучения с линейной x -поляризацией для кольцевой апертуры с 6 1 = 48 ° и 0 ₂ = 82 ° в случае различных значений коэффициентов c ₀, c ± 1 , c ± ₂. В отсутствие вихревой фазы на оптической оси имеется только x -компонента (первая строка табл. 3), наличие вихревой фазы первого порядка любого знака приводит к появлению продольной компоненты (вторая строка табл. 3), а наличие вихревой фазы второго порядка любого знака позволяет получить на оптической оси вклад y -компоненты (третья строка табл. 3). Заметим, что при x -поляризации вклад y -компоненты относительно мал (четвёртая строка табл. 3).

Таблица 2. Результаты моделирования фокусировки излучения с правой круговой поляризацией для кольцевой апертуры с 0 1 =48 ° и 9 2 =82 ° (интенсивность x-компоненты - сплошная линия, y-компоненты – штрихпунктирная линия, z-компоненты – точечная линия, общей – пунктирная линия)

Входное распределение: амплитуда (негативное изображение) и фаза

Интенсивность на оптической оси

c = 0,71, c = 0, c =- 0,71 U                 — 1           —2

c ₀ = 0, c _{— 1} = 1, c _— 2 = 0

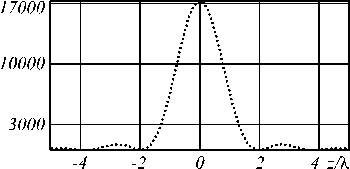
c ₀ = 0,71, c _{— 1} = 0,5, c _— 2 = 0,5

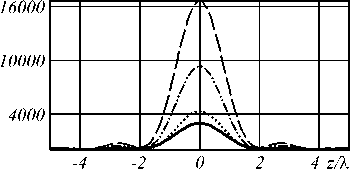
Заключение

В работе проведён анализ осевого распределения остросфокусированного лазерного пучка, представляющего собой суперпозицию вихревых фазовых функций, при различных поляризациях. Получено аналитическое решение для осевого распределения для каждой из компонент электрического поля при ограничении падающего пучка кольцевой апертурой произвольной ширины, в том числе при полной апертуре.

Также получены приближённые аналитические оценки для осевого распределения в элементарных функциях, позволяющие легко анализировать характер продольного фокального распределения. Эти оценки соответствуют узкой кольцевой апертуре и показывают, что для всех компонент электрического поля распределение интенсивности на оптической оси имеет примерно одинаковую зависимость sin² ( a x ) / x ², период осцилляций которой определяется шириной кольцевой апертуры. Полученные выражения могут быть использованы для оценки продольного распределения при фокусировке поля от различных колец, имеющих определённые значения фазы.

Численно исследовано влияние весовых соотношений суперпозиции вихревых фазовых функций в падающем пучке и типа поляризации (азимутальной, радиальной, круговой или линейной) на соотношение вклада различных компонент электрического поля в фокальную область на оптической оси.

Работа выполнена при финансовой поддержке гранта РФФИ 13-07-97004-р_поволжье_а, гранта Президента РФ поддержки ведущих научных школ НШ-4128.2012.9, а также Министерства образования и науки Российской Федерации, соглашение 8231.