Анализ параметров вибрационного поля города корреляционно-регрессионным методом

Автор: Вихоть А.Н., Лютоев В.А.

Журнал: Вестник Пермского университета. Геология @geology-vestnik-psu

Рубрика: Инженерная геология, мерзлотоведение и грунтоведение

Статья в выпуске: 1 т.20, 2021 года.

Бесплатный доступ

Проведен анализ параметров вибрационного поля города на примере территории Сыктывкара. Применяя методику корреляционно-регрессионного анализа и необходимые дополнительные расчеты, получили оценки математического ожидания, дисперсий и среднеквадратических отклонений, провели проверку нормального распределения случайных величин, получили значения коэффициентов корреляции и корреляционных отношений. Построены диаграммы распределения и выведены аппроксимирующие функции и эмпирические уравнения по компонентам x, y, z. Данный подход может быть использован для прогноза параметров вибрационного поля, позволяет дать рекомендации о его применении при выборе участков под строительные площадки и экологических изысканиях в области техногенной нагрузки.

Еще

Вибрационное поле, случайные величины, математическое ожидание, среднеквадратическое отклонение, коэффициент корреляции, коэффициент детерминации, экспоненциальная функция

Короткий адрес: https://sciup.org/147245083

IDR: 147245083 | DOI: 10.17072/psu.geol.20.1.49

Текст научной статьи Анализ параметров вибрационного поля города корреляционно-регрессионным методом

Территория любого города подвергается физическому загрязнению окружающей среды: воздушной, водной и геологической – вследствие воздействия техногенных нагрузок, к которым относится вибрационное поле. Вибрационное поле формируется из воздействия на геологическую среду различных динамических нагрузок, источниками которых выступают строительная техника, механизмы, ж/д и автотранспорт. В случае таких воздействий деформация грунта возрастает до 1%. Согласно (ГОСТ Р ИСО 52892–2007) передаваемая через грунт техногенная вибрация – это внешняя динамическая нагрузка техногенной природы в виде сейсмических волн, источниками которой являются взрывные и строительные работы, движение транспорта и др., оказывающая зданиям и сооружениям дополнительные механические напряжения. В этом случае геологическая среда является основанием фундамента сооружения, поэтому помимо изменений состояния самой конструкции вибрация косвенно вызывает изменения динамических и физико-механических свойств грунта, кото- рый служит основанием фундамента. Большинство авторов единогласно приходят к выводу, что к наиболее устойчивым к вибрации горным породам относятся увлажненные крупно- и среднезернистые пески, супеси и глины. Менее устойчивыми грунтами считаются водонасыщенные глинистые грунты, мелкозернистые и пылеватые пески, супеси и суглинки (Борисов, Алимов, 2007; Кушнарева, 2008).

Стоит отметить, на территории г. Сыктывкара уплотнение (первая фаза структурного изменения) наиболее ослабленных грунтов (тонко- и мелкозернистых песков) наступает при ускорениях вибрации 0,003g (Лютоев, Вихоть, 2019), что также является основанием изучения параметров вибрационного поля данного населенного пункта.В современной литературе больше всего освещено изучение вибрационного воздействия на геологическую среду и сооружения от движения ж/д и иного рельсового транспорта, менее – автотранспорта. Практические исследования проводятся точечно, исходя из производственных потребностей: они связаны в основном с устойчивостью склонов вдоль железных дорог, обеспечением надеж-

ности строительных конструкций, сохранностью памятников культуры (Алимов, 2006; Лютоев, Лютоева, 2016; Костарев, 2004 и др.). Меньше внимания уделяется изучению вибрационного поля городов, как экологическому аспекту вклада в физическое загрязнение окружающей среды.

Методы исследований

В отечественной и зарубежной нормативной литературе (ГОСТ Р ИСО 14837–1–2007; Чернов, 2006; DIN 4150–3–2016) из трех основных параметров вибрации за нормируемые приняты виброскорость и виброускорение.

Для определения параметров вибрационного поля была проведена вибросейсмиче-ская съемка методом виброметрии территории наиболее оживленного движения автотранспорта г. Сыктывкара. Сбор данных осуществлен в 212 точках в частотном диапазоне от 0,3 до 50 Гц. Период измерений составлял 3 минуты с двойным повтором в соответствии с (ГОСТ Р ИСО 52892–2007). Скорость записи данных 60000 знач/мин.

Расчет среднего квадратического значения – автоматический. Оси x и y имели горизонтальные направления N–S и E–W соответственно, ось z – вертикально вниз. Для регистрации входного сигнала виброускорения в работе использовалась сертифицированная аппаратура – широкополосная цифровая сейсмическая станция «ZET 048-C» в режиме «виброметр». Интегральные расчеты сигналов виброскорости и виброперемещения выполнены с применением сертифицированной расчетной программы «ZETLab Seismo».

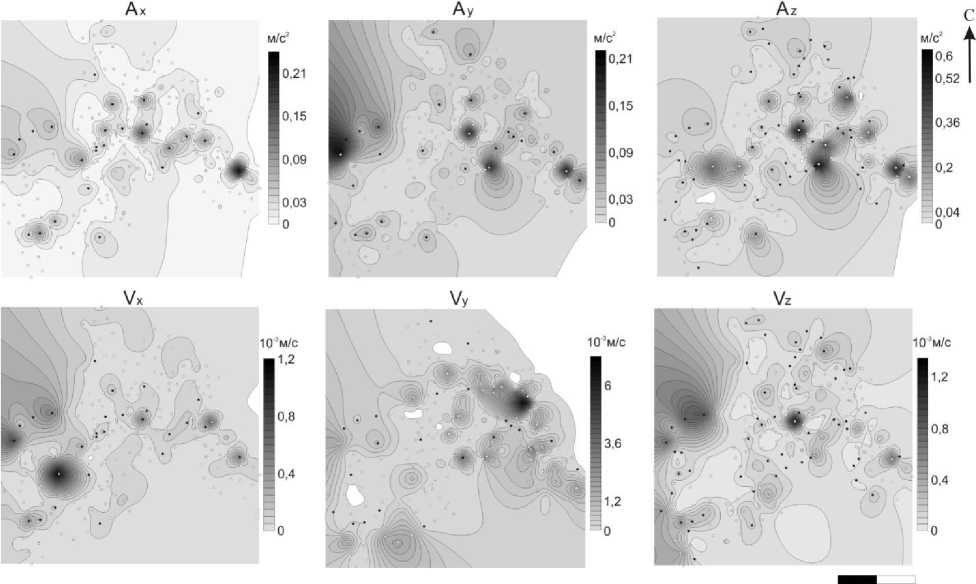
По результатам обработки данных было построено 9 схем с изолиниями по трем параметрам по трем компонентам, в расчетах будем использовать данные виброскорости и виброускорения (рис.1).

Обсуждение результатов

С целью проведения корреляционного и регрессионного анализа экспериментальных данных виброскорости и виброускорения в первую очередь была проверена гипотеза об однородности распределения данных.

О 500 1000 м

Рис. 1. Изолинии вибрационного поля г. Сыктывкара: A – виброускорения, V – виброскорости, черные точки измерения – реализации, вовлеченные в анализ

Таблица 1. Реализации виброускорения и виброскорости

№ТИ, единицы десятки		0	1	2	3	4	5	6	7	8	9
Компонента x
0	А, м/с²		0,035	0,038	0,084	0,151	0,034	0,035	0,091	0,043	0,069
0	V, 10^-3 м/с		0,096	0,102	0,154	0,443	0,118	0,099	0,071	0,133	0,011
1	А, м/с²	0,046	0,068	0,031	0,031	0,086	0,055	0,042	0,061	0,034	0,041
1	V, 10^-3 м/с	0,106	0,77	0,026	0,125	0,242	0,125	0,344	0,506	0,306	0,129
2	А, м/с²	0,073	0,086	0,041	0,036	0,041	0,07	0,084
2	V, 10^-3 м/с	0,167	0,204	0,081	0,065	0,076	0,157	0,216
Компонента y
0	А, м/с²		0,059	0,044	0,068	0,039	0,09	0,082	0,053	0,038	0,035
0	V, 10^-3 м/с		1,54	0,916	1,527	0,086	0,108	0,099	0,116	0,109	0,146
1	А, м/с²	0,033	0,04	0,03	0,033	0,103	0,031	0,154	0,033	0,048	0,03
1	V, 10^-3 м/с	0,892	0,073	0,092	0,305	0,54	0,337	0,677	0,219	0,218	0,511
2	А, м/с²	0,039	0,037	0,047	0,045
2	V, 10^-3 м/с	0,059	0,069	0,657	0,173
Компонента z
0	А, м/с²		0,071	0,059	0,034	0,108	0,06	0,102	0,03	0,053	0,141
0	V, 10^-3 м/с		0,085	0,063	0,078	0,098	0,088	0,178	0,035	0,163	0,185
1	А, м/с²	0,031	0,034	0,044	0,054	0,036	0,039	0,09	0,034	0,043	0,039
1	V, 10^-3 м/с	0,073	0,239	0,087	0,07	0,051	0,129	0,198	0,109	0,081	0,376
2	А, м/с²	0,093	0,031	0,055	0,045	0,066	0,038	0,034	0,056	0,074	0,056
2	V, 10^-3 м/с	0,096	0,068	0,037	0,157	0,178	0,08	0,063	0,181	0,164	0,099
3	А, м/с²	0,098	0,031	0,071	0,032	0,076	0,084	0,069	0,033	0,056	0,03
3	V, 10^-3 м/с	0,111	0,087	0,188	0,156	0,424	0,821	0,784	0,221	0,679	0,41
4	А, м/с²	0,037	0,031	0,056	0,04	0,035	0,03	0,061	0,09	0,123	0,172
4	V, 10^-3 м/с	0,091	0,041	0,256	0,256	0,049	0,05	0,15	0,117	0,14	0,181
5	А, м/с²	0,032	0,097	0,101	0,106	0,051	0,055	0,036
5	V, 10^-3 м/с	0,062	0,069	0,341	0,119	0,043	0,05	0,203

Из массива данных по компоненте x были отобраны случайные сверхнормативные среднеквадратичные значения – это > 0,03 м/с2 и исключено точечное значение 0,254 м/с2, резко выпадающее из выделенного диапазона реализаций 0,031–0,151 м/с2. Вероятно, опираясь на суждения по (Вихоть, Люто-ев, 2015) в данной точке измерений была зафиксирована работа высокочастотного источника колебаний или иного. Количество реализаций составило 26 (табл. 1). По компоненте y исключены значения 0,207; 0,201; 0,193; 0,191. Данные составили выборку 0,03–0,154 м/с2 (табл. 1). Диапазон по компоненте z – 0,03–0,141 м/с2 (табл. 1). Невостребованные данные: 0,365; 0,364; 0,32; 0,24; 0,269; 0,229; 0,183 м/с2. Оценки математического ожидания, дисперсий, среднеквадрати- ческих отклонений были найдены по формулам:

;

D(X) = M[(X – M(X))2];

σ(X) = √D(X).

Полученные по формуле V = σ/x̄ значения коэффициента вариации выборок во всех случаях составили более 33% (табл. 2). Это свидетельствует о том, что на данном этапе принять гипотезу об однородности распределения экспериментальных параметров нельзя. Выполним анализ данных по всем параметрам на однородность с помощью распределения Пирсона (хи-квадрат) с количеством степеней свободы k = n-1 на уровне значимости α = 0,05 (табл. 3) с помощью формулы: χ2 = Σ((ni – ni')2 / ni', где теоретическая частота ni' = (h · n/σe) · f(zi), стандартное отклонение σe = √De, где De = где zi = (xi – x̄e) / σe; h – длина частичного ин- (Σxi2 · ni) / n – (x̄e)2; выборочная средняя x̄e = тервала; f(z) – функция Гаусса; выборочное (Σxini) / n.

Таблица 2. Оценки статистических параметров

	Ax	Ay	Az	Vx	Vy	Vz
M	0,058	0,053	0,06	0,187	0,412	0,172
D	0,019	0,019	0,048	0,71	4,312	1,57
σ	0,139	0,14	0,219	0,843	2,077	1,253
V	2,399	2,651	3,664	4,496	5,044	7,302
ДИ	0,005;0,111	0,004;0,11	0,002;0,117	-0,136;0,511	-0,437;1,26	-0,157;0,5

Таблица 3. Оценка распределения Пирсона

Интервалы xi \		ni \	ni' \	σe \	De \	x̄ e	zi \	f(z) \	χ набл \	²χ кр
Ax
0,031–0,055	0,043	14	6	0,066	0,004	0,061	-0,279	0,383	16,69	9,5
0,055-0,079	0,067	6	6,22				0,084	0,397
0,079-0,103	0,091	5	5,65				0,447	0,36
0,103-0,127	0,115	0	4,49				0,81	0,287
0,127-0,151	0,139	1	3,13				1,173	0,2
Ay
0,03-0,054	0,042	16	4,017	0,063	0,004	0,053	-0,165	0,393	39,35	9,5
0,054-0,079	0,067	2	3,966				0,229	0,388
0,079-0,104	0,092	3	3,354				0,622	0,328
0,104-0,129	0,117	0	2,43				1,016	0,237
0,129-0,154	0,142	2	1,507				1,409	0,147
Az
0,03-0,048	0,039	25	5,748	0,068	0,005	0,062	-0,336	0,376	74,4	11,1
0,048-0,067	0,058	13	6,071				-0,063	0,397
0,067-0,085	0,076	6	5,951				0,21	0,389
0,085-0,104	0,095	7	5,414				0,482	0,354
0,104-0,122	0,113	2	4,572				0,755	0,299
0,122-0,141	0,132	3	3,584				1,028	0,234
Vx
0,011-0,163	0,087	17	6,266	0,235	0,055	0,171	-0,358	0,373	21,33	9,5
0,163-0,315	0,239	4	6,411				0,287	0,382
0,315-0,466	0,391	2	4,322				0,933	0,257
0,466-0,618	0,542	1	1,92				1,579	0,114
0,618-0,77	0,694	1	0,562				2,224	0,033
Vy
0,059-0,355	0,207	15	4,353	0,574	0,33	0,439	-0,404	0,367	30,60	9,5
0,355-0,651	0,503	2	4,693				0,112	0,396
0,651-0,948	0,8	4	3,877				0,628	0,327
0,948-1,244	1,096	0	2,454				1,144	0,207
1,244-1,54	1,392	2	1,19				1,66	0,1
Vz
0,035-0,166	0,101	37	10,924	0,234	0,055	0,18	-0,339	0,376	69,86	11,1
0,166-0,297	0,232	12	11,297				0,22	0,389
0,297-0,428	0,363	4	8,544				0,779	0,294
0,428-0,559	0,494	0	4,726				1,338	0,163
0,559-0,69	0,625	1	1,912				1,897	0,066
0,69-0,821	0,756	2	0,609				2,456	0,019

Для k = 4 и 5 и для α = 0,05 находим, что χ кр ² = 9,5 и 11,1 соответственно. Эти значения во всех случаях для Ax, Ay, Az, Vx, Vy и Vz < χ набл ², поэтому о гипотезу о законе нормального распределения параметров вибрационного поля с вероятностью 95% отвергаем. В связи с этим установим однородность реализаций по непараметрическим критериям, прибегнем к U-критерию Манна – Уитни. Соответственно получили 6 ранжированных рядов и 12 сумм рангов, пришедшихся на долю элементов первых и вторых выборок (табл. 4). По формуле по большей из ранговых сумм, имеющей вид:

U эмп = n 1 · n 2 + ((n x · (n x + 1)) / 2) – T x , установили, что все полученные значения U больше табличных и статистическая значимость различий между параметрами в рассматриваемых выборках не признается, поэтому анализируемые параметры вибрационного поля однородны. Далее можно перейти к корреляционному и регрессионному анализу.

Таблица 4. Оценка U-критерия Манна - Уитни

	Ax	Ay	Az	Vx	Vy	Vz
T 1	163	153	772,5	145,5	138	702
T 2	188	123	823,5	205,5	138	894
U эмп	72	39	366,5	54,5	72	296
U кр	51	38	291	51	38	291

Определим степень зависимости значения виброускорения от показателей виброскорости в точках измерения. Коэффициенты корреляции по компонентам x, y и z составили значения ниже среднего: 0,4; 0,25 и 0,15 соответственно – будучи вычислены по формуле Пирсона:

r = (Σ(x i – x̄) · (y i – ȳ))/(√(x i – x̄)² · √(y i – ȳ)²).

Оценка степени показала, что |ry/x| ≠ 0 и существенно <1, поэтому исключаем линейную связь между анализируемыми параметрами и найдем тесноту корреляции и степень функциональной зависимости между выборками Ax и Vx, Ay и Vy, Az и Vz: η = σмежгр/σобщ, где σмежгр2 и σобщ2 были рассчитаны по формулам: σмежгр2 = Σnx(ȳx – ȳ)2/n и σобщ2 = Σny(y –ȳ)2/n и составили 0,027; 0,029; 0,027 и 0,029; 0,029; 0,031 соответственно для компонент x, y, z. Частоты nxy наблюда- емых пар значений признаков составили не более 4. Полученные значения корреляционного отношения ηx = 0,93; ηy = 1; ηz = 0,87 удовлетворяют условиям: η ≥ |r| и η ≈ 1, что указывает на тесную корреляционную связь функционального типа между признаками A и V.

По данным табл. 1 построим диаграммы распределения (рис. 2). В качестве аппроксимирующих функций, исходя из подбора максимальных значений коэффициента детерминации, выберем экспоненциальную функцию. Получены эмпирические уравнения: 1) y = 0,043e1,002x; 2) y = 0,042e0,260x;

3) y = 0,049e^0,550x.

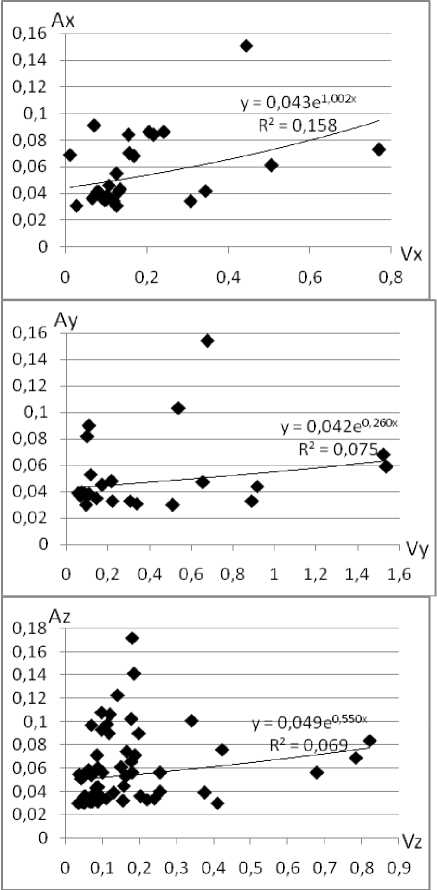
Рис. 2. Графическое выражение корреляционных связей вибрационного поля г. Сыктывкара по экспериментальным данным

Заключение

В результате проведенного корреляционно-регрессионного анализа вибрационного поля г. Сыктывкара получены коэффициенты корреляции, регрессии, уравнения функции распределения показателей, характеризующее данное поле и коэффициенты детерминации. Анализ данных показывает:

- полученные зависимости y = 0,043e^1,002x; y = 0,042e^0,260x; y = 0,049e^0,550x возможно использовать для прогноза параметров вибрационного поля на территории г. Сыктывкара;
- последствия вибрационного воздействия на грунтовую толщу и инженерные сооружения зависят не только от характеристик источников колебаний, только в некоторых случаях измерений прослеживается численное соотношение виброскорости и виброускорения, ведущее к определенным последствиям воздействия: просадкам грунтов, осадкам фундаментов и повреждениям строительных конструкций;
- остальные зависимости объясняются природными и климатическими факторами, повлиявшими и влияющими на физикомеханические свойства грунтов; это указывает на то, что следует весьма осторожно соотносить экспериментальные данные с нормативными или, например, с обобщенными данными по Восточно-Европейской платформе по (Жигалин, Локшин, 1987), учитывая поправки на геологические, гидрологические и геоморфологические условия;
- проводить исследования на предмет установления степени зависимости показателей вибрационного поля от геологических и гидрогеологических условий сразу на всей территории города затратно и трудоемко, поэтому такие работы в совокупности с описанным методом исследований рекомендуется осуществлять с целью обоснования выбора участков под строительные площадки и экологических изысканий в области техногенной нагрузки.

Статья научная