Анализ погрешностей аппроксимации корреляционно-спектральных функций ортогональными функциями Бесселя

1. ПОГРЕШНОСТЬ ОЦЕНКИ КОЭФФИЦИЕНТОВ РАЗЛОЖЕНИЯ ОРТОГОНАЛЬНЫХ МОДЕЛЕЙ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ

В БАЗИСЕ БЕССЕЛЯ

Представим ортогональную модель нормированной корреляционной функции (НКФ) P x ( т ) в виде [1]:

m

Pa1 Т ЕРк -Jv,к I-у),       (1)

к -0

где J v , к I- у ) – ортогональные функции Бесселя первого рода v - го порядка с параметром масштаба ортогональной функции у , к - порядок корня.

J„ (т, у) = J v [ A " ⁾ - (1 - e - 2 '" )]- e ^- Т (2)

Норма ортогональных функций Бесселя определяется из выражения:

w

J(Jv,к (т,у)-e^]-( Jn(ту)-e-у-т)-(1-e-2T )dT=

[ J M ⁾ ) k-n , = ⁿ;

4-у

=<

0, к * n.

где р(т , у ) = (1 - e ^{2 у-т} ) — весовая функция ортогональной функции Бесселя.

На практике вместо определения коэффициентов разложения ортогональной модели в соответствии с выражением [2]:

4 - у 7

Р к =     ₂ ,( v ). ^- J P x ^{(т )-} J . ^{( т} ,У ^)- ( ^{1 - e Т} ) ^{d T} (4)

J v + 1 ^(Лк ) 0

как правило, приходится ограничиваться конечным интервалом наблюдения корреляционной функции:

Л - ,      ^т к max

р1) = J Kx(т)-Jv,(т,У)-(1-e-r)d1, (5)

Jv+1 мкс ) о где Тк max - максимальный интервал корреляции;

При этом появляется дополнительная составляющая методической погрешности, вызванная конечным верхним пределом интегрирования:

aj; = Р - Рк =

= Т ⁴(^У^ h J K x ^{( т )- J} v , ^{( Т} , ^{У )- ( 1 -} e ^{- 2 Г ) d T} .⁽⁶⁾

J v + 1 ^(Лк ) Т к max

Необходимо отметить, что ^{lim А}д   0 .

^Т к max ^“

Специфика проведения аппроксимативного корреляционного анализа с помощью ЭВМ заключается в выборе численного метода для вычисления интеграла, «дискретизации» уравнений для оценки параметра масштаба у .

Обозначим оператор численного интегрирования Ф{}. Тогда оценка коэффициента раз-ло-жения, вызванная дискретизацией КФ и необходимостью численного интегрирования примет вид:

Р 2 =» { p , ( А Т - i ) - J v , к ( А т - i , у ) , J max } . (7)

где Дт - интервал дискретизации корреляционной функции, max

= ent

т, k max

Дт

’ а i   1,.., J max

В этом случае составляющая методической погрешности, вызванная дискретизацией КФ и необходимостью численного интегрирования, равна

Д 1 ⁾ = Р Г - Р к °. (8)

В связи с конечностью выборки значений КФ выражение для оценки коэффициента разложения представим в виде:

^Р = Ф{/ 9 x ( ^{Д т} i ) • J v k ( ^{Д т} • i . К ) ^{, Т} к max . N ^} - ⁽⁹⁾ где N – объем выборки.

Следовательно, составляющая методической погрешности, вызванная конечностью объема выборки, равна д /;=р(3) - /k2). (io)

Отметим, что для получения достоверных оценок (статистическая погрешность равна 0,020,05) количество отсчетов соответственно равно N=5000-2000.

Следующая составляющая методической погрешности вызвана необходимостью дискретизации уравнения и применения численных методов для оценки параметра масштаба К . Выражение для оценки коэффициента разложения в этом случае примет вид:

^ к ) ^ C x ( ^{Д т} i ) • V ( ^{Д т} ^ i . к ) ^{, T} k max , N ^} .(11)

Составляющая методической погрешности, вызванная заменой параметра масштаба К его оценкой К ,будет равна:

Д К ⁴⁾ = / ? _t ⁽⁴⁾ - / ?^ .            (12)

Перечисленные составляющие методической погрешности образуют полную группу погрешностей. Следовательно, методическая погрешность вычисления коэффициентов разложения определяется как:

^Д _{Р к} = ^Д / к ^+Д / ) ^+Д /к ^+Д К ⁴⁾ = р к ⁴⁾ - Р к . (13)

Конечность интервала интегрирования (интервала корреляции КФ) и применение численных методов интегрирования будут вносить в результирующую погрешность систематическую составляющую, а ограниченность выборки для определения значений КФ и оценки параметра масштаба К — случайную составляющую. Следовательно, составляющие погрешности Д / k *, Д^ можно определить, например, с помощью математического пакета MathCAD, а Д Р ¹. Д К' – методом имитационного моделирования, который реализован в системе.

Покажем это на примере.

На рис. 1 приведены результаты оценки коэффициентов разложения, полученные при по-

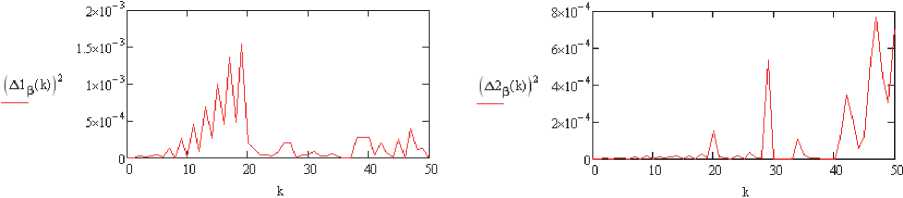
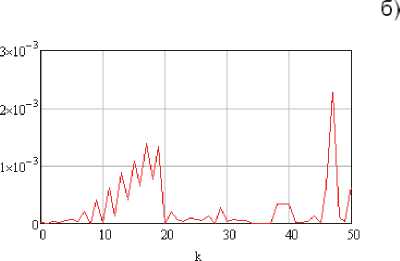
в)

Рис. 1. Результаты оценки коэффициентов разложения, полученные при помощи пакета MathCAD: а –дополнительная составляющая методической погрешности, вызванная конечным верхним пределом интегрирования, б – составляющая методической погрешности, вызванная дискретизацией КФ и необходимостью численного интегрирования (метод Симпсона), в - методическая погрешность вычисления коэффициентов разложения / _к

мощи пакета MathCAD, со следующими исходными данными:

• -    ^ ( т ) = exp ( -Л-Т ) • COS ( to ₀ -т ) с отношением to ₀ / Л = 5/1, А т = 0,0816 и числом ординат Nx = 37 , объемом выборки N = 5000 ;

• -    диапазон порядка коэффициента к = 0.. m , m = 50;

• -    параметр масштаба ортогональных функций Бесселя первого рода 0-го порядка у = 0,096 .

На рис. 1:

• а)    А 1 р ( к ) = р *” - Р ;

• б)    А 2 р ( к ) = р ^ ²⁾ - Р^¹ , метод интегрирования – Симпсона;

• в)    А сист р ( к ) = А 1 р ( к ) +А 2 р ( к ) = р (²⁾ - [ k .

• 2.    ПОГРЕШНОСТЬ АППРОКСИМАЦИИ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ОРТОГОНАЛЬНЫМИ ФУНКЦИЯМИ БЕССЕЛЯ

  Из рис. 1 видно, что при дальнейшем увеличении числа членов ряда значение погрешности, обусловленной конечностью интервала интегрирования, уменьшается, однако погрешность, обусловленная применением численных методов интегрирования, напротив, растет с увеличением порядка k, следовательно, как и систематичес-

  
  

  Запишем погрешность аппроксимации КФ в виде:

  
  

  W

  
  

  m

  
  

  А= J K , ( т ) -0 2 • £/ J k • J _{V 1}

  0 L                k = 0

  x ( 1 - e ^{- 2} ^ ) dT ^ min

  
  

  I X

  
  
  
  
  

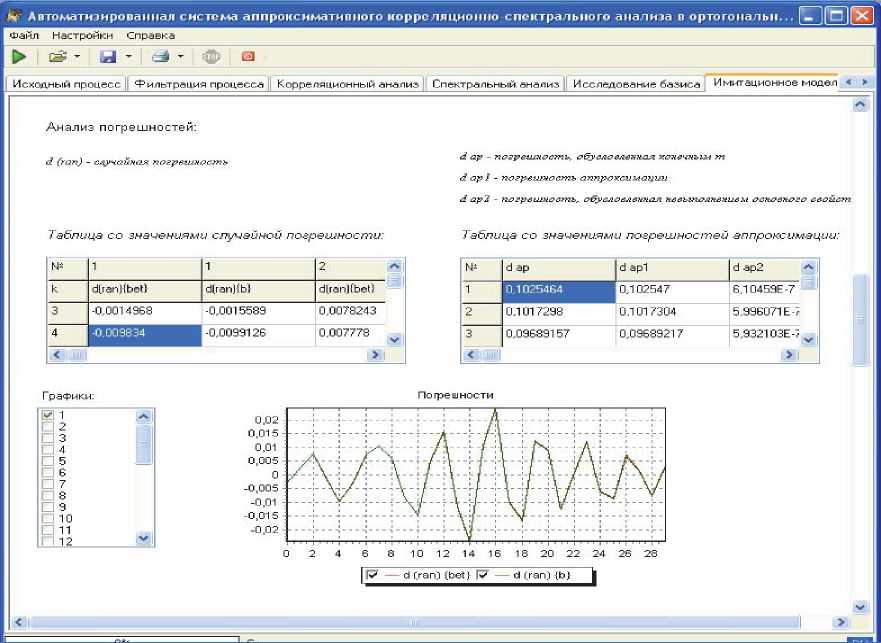
  Рис. 2. Результат оценки составляющей методической погрешности, вызванной конечностью объема выборки методом имитационного моделирования с помощью автоматизированной системы аппроксимативного корреляционно-спектрального анализа случайных процессов в ортогональном базисе Бесселя

  
  

кая составляющая методической погрешности оценки коэффициента разложения.

На рис. 2 приведен результат оценки составляющей методической погрешности, вызванной конечностью объема выборки, т.е. d ( ran ) = А Р 3) = р^ (^ - [ (2 , полученный методом имитационного моделирования с помощью автоматизированной системы аппроксиматив-но-го корреляционно-спектрального анализа случайных процессов в ортогональном базисе Бесселя (АИС «АКС Бессель»).

Необходимо отметить, что погрешность определения коэффициентов разложения А„ возрастает р с увеличением порядка k и является случайной величиной, распределенной по нормальному закону.

где Pk — оценка коэффициента , у - оценка параметра масштаба .

Используя формулу (3), перепишем выражение (14) в виде:

W

Д= I KX(T)\1-e -^) dT -

У4

2-Г

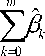
m

ˆ

• Р _к - J .М ) )+

У ⁴

•• 1

4 • у к о

Данное выражение является функцией случайных оценок коэффициентов разложения P k . Считая отклонение оценок от коэффициентов разложения малыми, разложим выражение в ряд Тейлора относительно p k в окрестности p _k , ограничившись квадратичными членами:

W

Д = I KpT) - (1 - e ^T ) d T -

4 m

- - - 1 P • J v + 1 ^ ^+

4 • у к = о

4 m ₂

+, • 1 ( P k - P k ) • J v . - ) )

^{4 -} У к = о

В общем случае оценка коэффициентов разложения P k смещена, поэтому

o

R = P . P +Д         (17)

kkk   cm , k

С учетом того, что

Д т. = | K , ’( T )- ( 1 - e ^{- 2} * ) dT -

4 m

-    - 1 P 2 • J v +1W ) ),

4 • у к "0

погрешность аппроксимации приведем к виду:

Д = Д . + Д , min m ^,

-4 тц Г       У где Дm = ~^- 1[ Рк + Д см,к I • Jv +1 ^к ) .

4 • у к = о к            )

Математическое ожидание погрешности аппроксимации равно:

M [ Д ] = Д min + M [ Д m ] =

4 m

= Д.+ ^п, -У - ² + Д ² • J ²^v ^v ) ) . (19) ^min д ? Z—i \ x       cm , к / ^{v + 1 V к} J

4• у к = 0

Видно, что математическое ожидание погрешности аппроксимации, кроме минимальной погрешности, содержит вторую составляющую, численное значение которой линейно зависит от погрешности оценки коэффициентов разложения и увеличивается с увеличением числа членов разложения ряда m. Следует отметить, что в общем случае с увеличением числа членов разложения ряда A _min уменьшается. Следовательно, существует минимум погрешности по m. Далее покажем это на примере (см. рис. 3).

Выполнив все необходимые преобразования, получим дисперсию погрешности аппроксимации:

^{8 mm}                00

- Д = ^Р"- • 11 Jv+ iW ) ) • Jv + i ² ( ^ n^v ) ) • M ^ к ^.

16 - к = о П = о                                L

8 m

= Т7к5 - 1 Jv . i ‘ ^ ' '' -2- к +

16 - у к = 0

8 m

+ r x 2 - 1 Jv - 1 ² ( ^Л к ") ) - J- - 1 ² ( ^ ( ' ) ) - K_t . к , . ,

^{8 -} г к ^ .

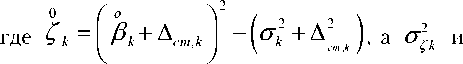
K ^ _к. - дисперсия и корреляционный момент случайной величины ^ .

При условии некоррелированности

^ к ^_п ( ^К ; к. = 0 ) получим:

^{8 m}

2 ^У х              4/')( v )\2 ^2

^— Д = 1 _А 2^- 1 J v + 1 ⁽ ^к ) "^У; к .    (20)

16 - Y к~0

2 ^o

Оценим У ^_к . Закон распределения P ^^ , так как выполняются условия теоремы Ляпунова, можно считать нормальным. Тогда

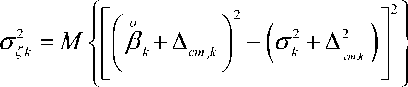
cm k

= 2- - 4 + 4- - 2 -Д

Окончательно получим:

8 _m

2 = 87 x 2 ^- к =0 ^J v •'('^ ^{) ) 2 -} - ² 'I - '^{+ 2} '^A L ) . (21)

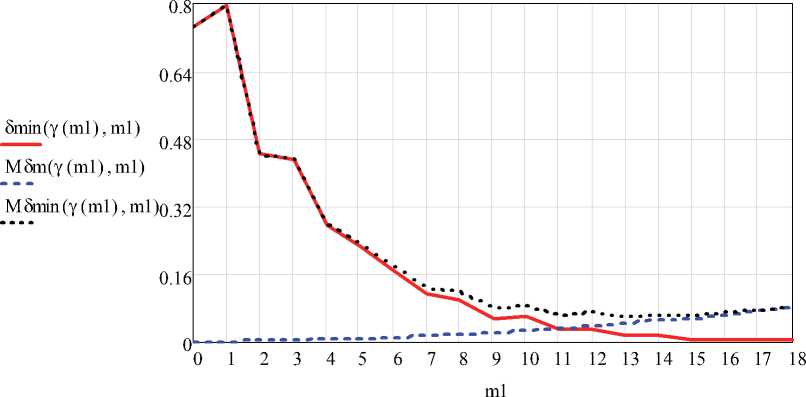
Рис. 3. Квадратические погрешности приближения при оценке коэффициентов разложения, полученные при помощи пакета MathCAD

Из данного выражения следует, что дисперсия погрешности аппроксимации растет с увеличением числа членов разложения ряда m, а её численное значение зависит от дисперсии и погрешности от смещенности оценки коэффициентов разложения ряда.

На практике, как правило, оценивают относительную погрешность аппроксимации:

~                     - ^ min ⁺ S _m , (22)

JKx (r)-(1 - e-Y)dr 0

mo ²

^p , + Д cm , k I • J. ^ ) )

где ^ m ^— ~--W----------------

⁴ • Y* J K X ( ^T ) ^- ( 1 ^- e ^{- 2 YT} ) d ^T

m

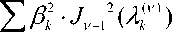
k — 0

w

а ^min — 1 -

4 • Y-J Kx (t)-(1 - e-2YT) dT

m

•U.MV-0 - ( С +2-Д_ ) .

k - 0

2 w

»1Y - JKt.') dr

На рис. 3 приведены квадратические по- грешности приближения при оценке коэффициентов разложения, полученные при помощи пакета MathCAD, со следующими исходными данными:

• -    p^T) — exp(-A-T )• cos (too-T) - с отноше

  нием ^ 0 / Я — 5/1, Д т — 0,0816 и числом ординат к — 0.. m , m — 18;

• -    диапазон порядка коэффициента к — 0.. m , m — 18;

• -    параметр масштаба ортогональных функций Бесселя первого рода 0-го порядка Y — 0,258 .

m

Ё - ^ k ¹ - J . .^-Я" ) )

^ min ( Y , m ) ^— 1-- k 5 °-----------------------

4-Y-JKx (t)-(1 -e-1T)dr ;

m

Ё-Yk- J. ;чяг ))

M^ m ( Y , m ) —----w⁰-----------------

• 4-    Y-JK.2 (t)-(1-e-2Y)dr;

^{M 5} mn ⁽ Y , m ) ^— ^ min ⁽ Y , m ) + M 5 m ⁽ Y , m ) ^.

Рис. 3 описывает процедуру поиска миниму-ма-миниморума суммарной погрешности, обеспечивающего оптимальный выбор m.

На рис. 4 представлена зависимость оптимального числа членов разложения ряда m от параметра масштаба у для описанных выше исходных данных.

Значение методической погрешности зависит, главным образом, от способа оценки пара-

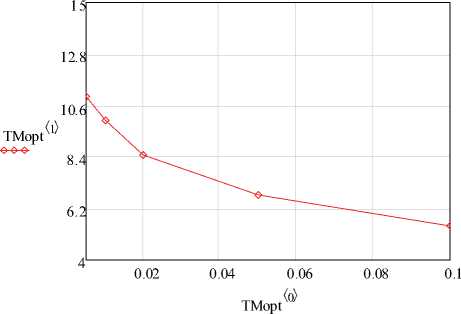
Рис. 4. Зависимость оптимального числа членов разложения ряда m от параметра масштаба у (по оси ординат - m, по оси абсцисс - у )

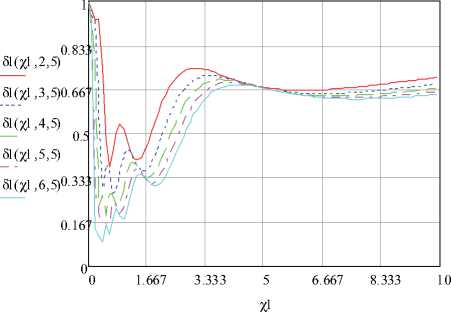
Рис. 5. График относительной погрешности аппроксимации при to = 5 и m = 2 ^ 6

метров модели, а, в частности, параметра масштаба, обеспечивающего минимальную допустимую погрешность аппроксимации.

Вид ортогональных функций Бесселя аналогичен виду функций Дирихле, а, следовательно, данные функции имеют близкое значение коэффициента формы, определяемое из выражения [3]:

На рис. 5 представлена зависимость относительной погрешности аппроксимации от параметра масштаба при различных значениях числа членов разложения ряда m = 2 ^ 6 и показателе колебательности to = 5 для ортогональных функций Бесселя.

В качестве аппроксимируемой функции вы-

^Кф а Ш =

ТО

J Р а ( ^Т ) ( 1 - g ^Л^ 0

ТО

J Р а ( ^Т ) g ( ^Т , 5 ) d T

берем НКФ p x ( t ) = e ^Хт cos to ₀ T .

3. ПОГРЕШНОСТЬ ОЦЕНКИ СПЕКТРА ПО ПАРАМЕТРАМ МОДЕЛИ КФ

где g ( t , ^ ) = e ^- ^ ^Т , так как ортогональные функции имеют экспоненциальный вид, а параметр ^ выбирается в соответствии с длительностью аппроксимируемой КФ.

Следует заметить, что вес ортогональных функций Бесселя, в свою очередь, аналогичен весу ортогональных функций Якоби с параметрами а = 0 , Р = 1 , что позволяет говорить об общности подхода к построению ортогональных моделей в указанных ортогональных базисах.

Кроме того, заметим, что алгоритм оценки параметра масштаба у ортогональных функций Дирихле и Якоби (0, 1), а, следовательно, и ортогональных функций Бесселя, идентичен.

Таким образом, для ортогонального базиса Бесселя параметр масштаба определяется из выражения:

Погрешность спектра КФ по параметрам аппроксимирующего выражения можно пред-ста-вить в виде [4, 5]:

ТО

0 _

а

^А = J S ^{( to )} —- • S ^P ■ Re WAj ^-to ) d to (26) n           ^ =0

k = 0

Wk ( j to ) + W_k ( - j to ) где Re W _k ( j to ) = ——— ' 2 ^kX —-—- ,

1        ( TO " I а Wk (jto) =       • I 1 + S П M,   (27)

у + j to (       ,,= t / ^{v 7}

a. = (-1)(Л )2-----1 1 + i Ix i V kV k) i + 112 )

^х л.

f 3 ^{У + j to} + 2 i lf 1 + 3 ^{У + j to} + 2 i |

( 2 у )(       2 у j

0,4

у =---------

(m + 1)-Аг0 .

Для колебательных моделей с погрешностью восстановления 2% справедливо

^{А Т} 0

0,4

V ^ + ^ 02 .

Раскрыв квадрат подынтегрального выражения, получим:

TO                   2 ^ o² m TO

^А = J ( ^ x ( ^to ) )^{2 d to} --- • T p kk • J S x ( ^to ) • Re W k ( j • ^to d ^{to +}

0                    ^{Л k} = 0 0

O’ ^{m m         TO}

⁺“T TS jkk • P l" J ^Re W k ( j • ^to ) • ^Re W ( j • ^to ) ^{d to}-

^ k = 0 l = 0        0

С учетом того, что [6]

P k —

2 • Y

J ,_{+ 1}²(^ k ^{v )} )

w

J S , (to) • Re W k ( j •to ) d to , (28)

w

J Re Wk (t, y ) • Re Wt (t, y) dT —

— <

J 1W)H _k=i _;

8 • y ’       ’

0, k * I .

приведем выражение для погрешности оценки спектра к виду:

• 7,                  ст²      -

• A=J(S,(to)) dto- —^■£# • J,.WV (30) 0         8^ Y t0

• 3.    ПОГРЕШНОСТЬ ОЦЕНКИ

Поскольку для корреляционно-спектральных характеристик справедливо следующее выражение:

w                   w

J( S , ( to ) )² d to = —J( K , ( t ) ) ² - ( 1 - e ^-* ) d T _yl) 0.                    ² •” 'o

Окончательно запишем погрешность оценки спектра как

-2 / ”                       m     T ²      A

^A = ^Y, • J( K x T ^J ' "') dT-ТЙ ■ J t (^ i" ) - (32) ^2-Л ^ ₀                     1 = 0    4'^Y     J

КОРРЕЛЯЦИОННО-СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК

В АИС «АКС Бессель» приводится расчет таких погрешностей корреляционно-спектральных характеристик, таких как:

• -    относительная погрешность интервала корреляции -r k ^{2 )} [2]:

₂ ( ² )     2 ( ² )ч /2( ² )

V ( 2 ) — (T 1      T k ) T k

^T k

m где т2) —     /?;(3)т((2И);

k k k , u k—0

• -    относительная погрешность оценки интервала корреляции ^ ^{4 )} [2]:

V ( 4 ) = ⁽T k ^{4)- T} k ^{4 )} ) / ^t1⁴⁾ , ^T k

m где тk4) — E P^t<^).

k — 0

• -    относительная погрешность оценки экстремальной частоты спектра – частоты, соответствующей последнему максимуму спектральной плотности мощности:

  ^V to ₃ ^{— ( to} э ^{- to} 3 )/ ^to 3 ,

  

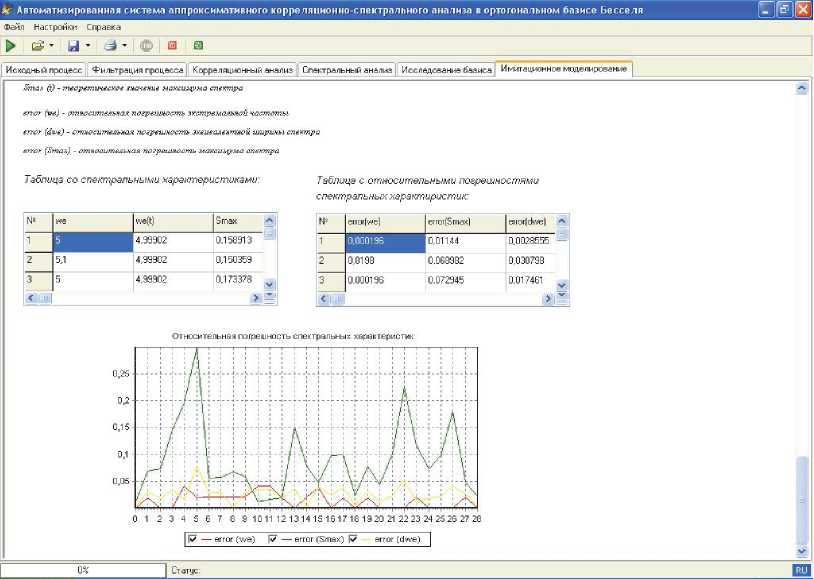
  Рис. 6. Результат вычисления погрешностей оценки корреляционно-спектральных характеристик методом имитационного моделирования с помощью автоматизированной системы аппроксимативного корреляционно-спектрального анализа случайных процессов в ортогональном базисе Бесселя

  
  

  - относительная погрешность оценки эквивалентной ширины спектра [2]:

  •Ч ^{— ( а&} э ^{X to} ^to ,

  
  

  А to э

  
  
  
  

  где 1

  
  

  2 S x ( to , )

  
  

  А to э

  
  

  — to э +

  
  

  А to э

  
  

  А to ' — ----- ¹--;---

  э ² S , ( to ) ^{x э} max

  А to₃ — to₃ + А to '12

  
  

  - относительная погрешность оценки максимума спектра:

  
  

  g        _— ^{S x (to э} ) max ^{S x (to} ) max

  ^{Sx ( to ) max}                s_x ( to )                .

  ^{x э} max

  На рис. 6 приведен результат вычисления погрешностей оценки корреляционно-спектральных характеристик методом имитационного моделирования с помощью АИС «АКС Бессель» со следующими исходными данными:

  • -    р ( т ) — exp ( -A-T ) • cos ( to ₀ -т ) с отношением to ₀ / X — 5/1, А т — 0,0816 , числом ординат Nx — 37 , объемом выборки N — 5000 ;

  • -    диапазон порядка коэффициента к — 0.. m , m — 18;

  • -    параметр масштаба ортогональных функций Бесселя у — 0,25 8.

  
  

  ЗАКЛЮЧЕНИЕ

  1. Определена погрешность оценки коэффициентов разложения ортогональных моделей

  
  

  КФ в базисе Бесселя.

  • 2.    Получена погрешность аппроксимации КФ ортогональными функциями Бесселя.

  • 3.    Приведен алгоритм оценки параметра масштаба, гарантирующего минимум квадратической погрешности приближения для ортогональных функций Бесселя.

  • 4.    Определена погрешность оценки спектра по параметрам аппроксимирующего выражения КФ.

  • 5.    Определены погрешности оценки корреляционно-спектральных характеристик.

  СПИСОК ЛИТЕРАТУРЫ

  • 1.    Прохоров С.А., Газетова Я.В. Автоматизированная система аппроксимативного корреляционно-спектрального анализа в ортогональном базисе Бесселя // Известия высших учебных заведений. Поволжский регион. Технические науки. 2010. №2 (14). С. 30-40.

  • 2.    Прохоров С.А., Куликовских И.М. Ортогональные модели корреляционно-спектральных характеристик случайных процессов. Лабораторный практикум Самара: СНЦ РАН, 2008. 301 с.

  • 3.    Прохоров С.А., Газетова Я.В., Куликовских И.М. Автоматизированная система аппроксимативного корреляционного анализа в ортогональном базисе Бесселя // Труды седьмой Всероссийской межвузовской научно-практической конференции «Компьютерные технологии в науке, практике и образовании», СГТУ, Самара, 2008. С. 13-16.

  • 4.    Прохоров, С.А., Куликовских И.М. Погрешность оценки спектра по параметрам аппроксимирующего выра-жения корреляционной функции // Математическое моделирование и краевые задачи: труды пятой Всероссийской научной конференции с международным участием. Ч.4. Самара, 2008. С. 116-120.

  • 5.    Прохоров, С.А., Газетова Я.В. Частотные характеристики ортогональных функций Бесселя // Радиотехника и связь: Сборник научных трудов. – Саратов, 2009. С. 28-35.

  • 6.    Прохоров, С.А., Куликовских И.М. О некоторых свойствах ортогональности // Информатика, моделирование, автоматизация проектирования (ИМАП-2009): сборник научных трудов Российской школы-семинара аспирантов, студентов и молодых ученых. Ульяновск, 2009. С. 195-197.