Анализ поведения сигнала ядерного спинового эха в намагничиваемом феррите

ВВЕДЕНИЕ                           МЕТОДИКА

Ядерный магнитный резонанс (ЯМР) уже достаточно давно используется как метод изучения соединений, обладающих магнитным порядком [1], и, будучи инструментом, дающим о магнитном состоянии многообразную информацию, постоянно развивается [2]. Прогресс стимулируется появлением новых веществ; в настоящее время к ним преимущественно относятся магнитоупорядоченные наноструктуры, которые часто исследуются с помощью ЯМР (см. [3, 4] и содержащиеся там ссылки). Существуют и другие направления радиоспектроскопии магнитных материалов, например, известно, что посредством ЯМР регистрируются некоторые особенности строения кристаллической решетки [5, 6]. Для последних из упомянутых работ особо важны вопросы, связанные с наблюдением отклика ядерной спиновой системы в доменах и доменных границах, что и в целом представляет собой одну из актуальных проблем ЯМР-спектроскопии магнетиков [7, 8].

Настоящая работа посвящена изучению нестационарного ЯМР, наблюдаемого в некотором модельном образце, намагничиваемом внешним полем. При этом предполагается, что сопоставление статических магнитных характеристик материала с радиоспектроскопическими данными дает адекватную картину возбуждения ядерных спинов в системе электронных магнитных моментов, относящихся как к доменам, так и к доменным границам, что важно для уточнения принципов применения ЯМР к исследованию магнитоупорядоченных веществ.

Наблюдение ЯМР

ЯМР в настоящей работе регистрировался по сигналу двухимпульсного спинового эха ядер ⁵⁷Fe, возбуждаемого в феррите. Опыты выполнялись по схеме, обычной для данной области радиоспектроскопии. Образец помещался в катушку настроенного на частоту ЯМР ω n резонансного контура, на который с генератора подавалась последовательность двух радиочастотных (РЧ) импульсов, далее вместе с откликом образца в виде сигнала эха поступающая на вход приемной системы, в качестве которой использовался супергетеродинный приемник, снабженный широкополосным предусилителем. Длительности импульсов τ 1,2 изменялись в пределах нескольких микросекунд, основные измерения происходили при τ 1 = τ 2 = 2 мкс. Интервал между импульсами составлял десятки микросекунд. Амплитуды РЧ-импульсов достигали на катушке максимального значения в десятки вольт и могли быть уменьшены аттенюатором, расположенным между импульсным генератором и контуром.

Поскольку, как известно [1, 2], внешнего постоянного магнитного поля для наблюдения ЯМР в магнитном материале не требуется, сигнал эха был виден и при его отсутствии. В нашем случае, однако, поле к образцу прикладывалось, но его назначение в отличие от обычного ЯМР заключалось, как было сказано выше, в управлении магнитным состоянием вещества. При каждом новом значении внешнего поля резонансная частота контура подстраивалась до наибольшего сигнала эха.

Образцы, магнитные измерения и геометрия эксперимента

В качестве объекта исследований нами был выбран хорошо изученный с радиоспектроскопической точки зрения феррит — литиевая шпинель с добавкой цинка, Li 0.425 Fe 2.425 Zn 0.15 O 4 . Линия ЯМР в нем сглажена и имеет максимумы на частотах вблизи 68 и 71 МГц соответственно для комнатной температуры и температуры жидкого азота, при которых выполнялся эксперимент. С целью увеличения интенсивности эхо-сигнала материал был обогащен изотопом ⁵⁷Fe до 85%.

Использовался образец в виде двух одинаковых колец с внешним диаметром 1.1 см, внутренним 0.4 см и толщиной 0.35 см. Кольца были составлены таким образом, чтобы между ними образовался узкий (0.5 мм) зазор, в который помещался датчик Холла. На рис. 1 показаны расположение этих элементов и ориентация образца относительно внешнего постоянного магнитного поля H 0 , которое создавалось либо электромагнитом, либо, для небольших полей (до 370 Э), катушками Гельмгольца. При малом размере зазора можно положить его размагничивающий фактор равным нулю и считать, что датчик измеряет магнитную индукцию B внутри вещества. Тогда B = H 0 – 4 πξ M , где М — искомая намагниченность материала; ξ ≅ (1 – – N /4 π ) — коэффициент, учитывающий влияние размагничивания; а N — размагничивающий фактор колец в направлении, перпендикулярном их

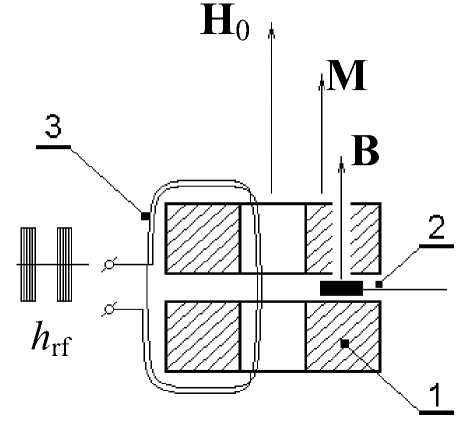
Рис. 1. Геометрия эксперимента.

1 — образец (в виде двух колец, показанных в продольном сечении); 2 — датчик Холла; 3 — катушка возбуждения (на ее зажимах изображены РЧ-импульсы, создающие внутри образца переменное поле h rf )

плоскости. Конечно, здесь это выражение применено не вполне корректно, т. к. при указанной геометрии пространственное распределение намагниченности нельзя считать однородным, однако опытным путем нами было установлено, что оно является хорошим приближением. Экспериментами с несколькими другими образцами того же состава, но имеющими форму тонких длинных цилиндров, было продемонстрировано, что вид кривых намагничивания для этих случаев различается мало. Далее будут приведены данные для величины 4 πξ M .

На кольца (рис. 1) была намотана катушка из нескольких витков, которая входила в резонансный контур и являлась одновременно возбуждающей и регистрирующей. Очевидно, что создаваемое ею импульсное радиочастотное магнитное поле h rf замыкалось внутри феррита, т. е. всегда оставалось перпендикулярным H 0 .

Магнитометрический и радиоспектроскопический тракты системы не оказывали влияния друг на друга, и наблюдение спинового эха можно было вести как раздельно, так и одновременно с записью магнитных параметров.

РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ

Данные магнитометрии

На рис. 2 показана зависимость 4 πξM от внешнего поля (пример начальной кривой намагничивания, снятой из полностью размагниченного состояния), которая была получена совместно с измерением амплитуды сигнала ЯМР. Из нее была определена намагниченность насыщения 4 πξM s ≅ ≅ 1700 Гс, позволившая оценить, с учетом данных [9], величину N /4 π , оказавшуюся равной приблизительно 0.7. Гистерезис (вставка на рис. 2), как и следовало ожидать для магнитомягкого материала, проявлялся слабо и уверенно регистрировался датчиком Холла только при H 0 < 300 Э. Хотя при разных внешних полях наклон кривой M ( H 0 ), разумеется, изменялся, каких-либо существенных особенностей, соответствующих характерным изменениям в поведении сигнала эха выявить на ней не удалось. (Более того, даже ее условное разграничение на области вращения, а также обратимого и необратимого смещения границ, принятые при классическом описании процесса намагничивания [10], в нашем случае сталкивалось с известными трудностями).

Удовлетворительную (по крайней мере до H 0 = = 1500–2000 Э) аппроксимацию начальной кривой давала функция M ( H 0 ) = M as arctg( α H 0 ), где M as и α — подгоночные параметры. Для ветви М ( Н 0 ), отвечающей снижению H 0 , применялась функция, учитывающая остаточную намагниченность M R :

M ( H 0 ) = M as arctg( α H 0 ) + M R . Определенные подгонкой величины M as , α и M R использовались далее в расчетах.

За начало области вращения (т. е. такой, где доменные границы считаются отсутствующими)

было принято поле, при котором M составляет примерно 80 % от M s [10]. Из рис. 2 видно, что это происходит при H R ≅ 1800 Э ( М = 1400 Э); наклон экспериментальной кривой намагничивания d M / d H 0 здесь заметно уменьшается.

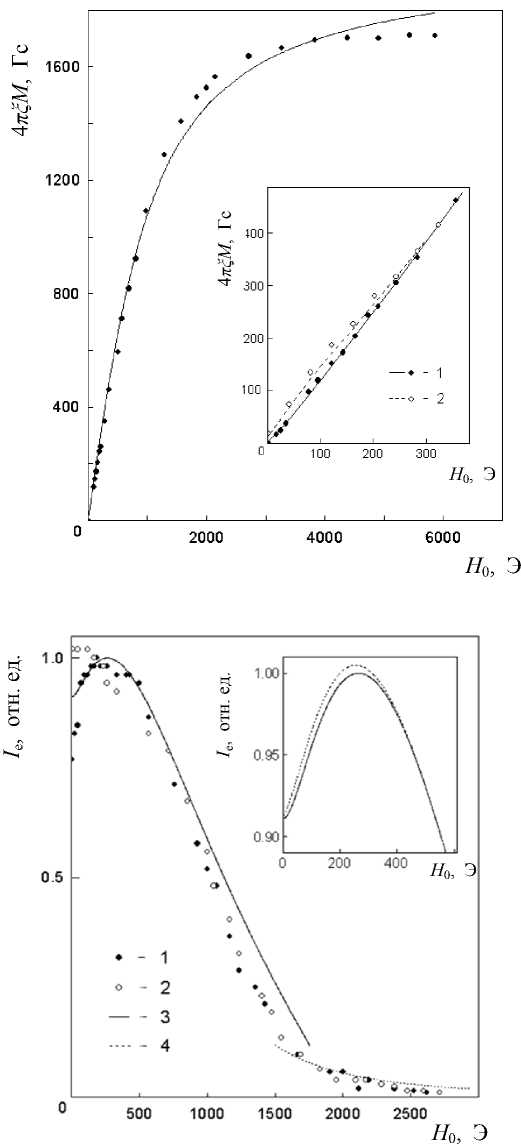
Рис. 2. Начальная кривая намагничивания феррита при комнатной температуре.

Сплошной линией показана аппроксимация экспериментальных точек функцией M ( H 0 ) = M as × × arctg( α H 0 ). На вставке: начальный участок кривой, демонстрирующий наличие гистерезиса, 1 — прямой ход, 2 — обратный ход (аппроксимирован функцией M ( H 0 ) = M as arctg( α H 0 ) + M R )

Рис. 3. Зависимость амплитуды сигнала спинового эха от постоянного магнитного поля.

1 — прямой ход; 2 — обратный ход; 3 — расчет с использованием модели поликристаллической среды и данных аппроксимации; 4 — расчет полевого поведения сигнала от доменных границ, выполненный с учетом выражения (1). На вставке: результаты модельного расчета на прямом (сплошная линия) и обратном (пунктир) ходе в области максимального отклика

Данные ЯМР

Поведение амплитуды спинового эха I e от постоянного магнитного поля показано на рис. 3 и 4. Характерный признак этой зависимости, состоящий в наличии участка возрастания сигнала при увеличении H 0 (присутствие которого, казалось бы, противоречит обычным представлениям о свойствах ЯМР в магнитоупорядоченных веществах [1]), отмечался и ранее, например в [11]. Законченного объяснения он не получил, хотя несомненной представлялась его связь со сложной природой отклика ядерной спиновой системы в многодоменном поликристалле. Последнее положение подтверждается еще одной особенностью I e ( H 0 ), отмеченной в наших экспериментах, а именно существованием сильного гистерезиса, существенно превышающего гистерезис кривой намагничивания. Особо следует отметить то, что он не только количественно, но и качественно определялся тем максимальным значением, до которого увеличивалось H 0 . В частности, сравнение рис. 3 и рис. 4, а, демонстрирует существенное различие кривых, полученных при разных максимальных значениях, до которых поднималось поле: в первом случае ( H 0max = 2700 Э) расхождение прямой и обратной ветвей I _e( H ₀) происходило приблизительно при 700 Э, а сами эти кривые шли с пересечением около H 0 = 170 Э, во втором ( H 0max = 370 Э) расхождение возникало при H 0 = = 270 Э, а пересечение отсутствовало. Отметим, что снижение температуры до азотной значительно преобразовывало вид I e ( H 0 ) (рис. 4, б).

При возвращении к нулевому полю амплитуда эхо-сигнала отличалась от той, с которой начинался процесс, однако после проведения циклического перемагничивания образца она восстанавливалась до исходного значения.

Выше H _R, принятого нами за границу области вращения, ход зависимости I e ( H 0 ), как это видно из рис. 3, изменялся, переходя к более плавному снижению.

ОБСУЖДЕНИЕ

Исходные теоретические сведения

Для дальнейшего нам потребуются основные представления о характеристиках ЯМР в магнитном материале. Следуя [1, 2], будем считать, что спиновая система в доменах и доменных границах возбуждается с разными коэффициентами усиления η d и η w соответственно. Для первой из этих величин получено выражение

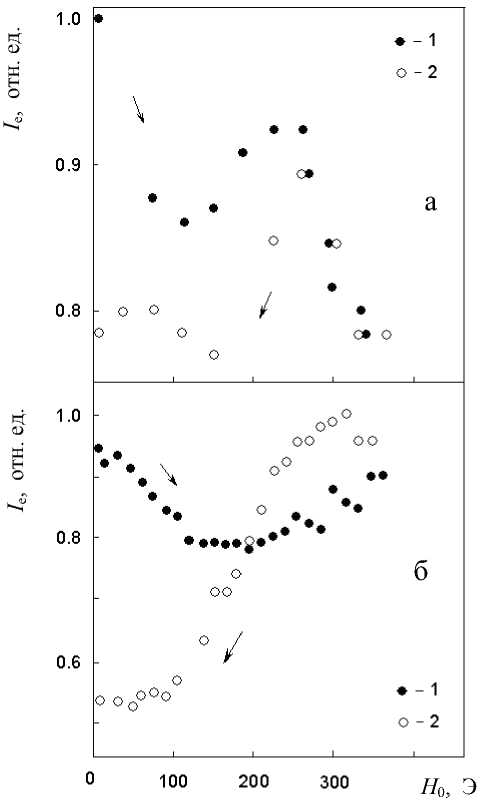
Рис. 4. Поведение амплитуды сигнала спинового эха при перемагничивании образца в малых полях при (а) комнатной температуре и (б) температуре жидкого азота.

1 — прямой ход, 2 — обратный ход где Hn — локальное поле на атомном ядре (преимущественно сверхтонкого происхождения), созданное электронной намагниченностью, а Ha — эффективное поле магнитной анизотропии. Вид выражения для ηw, вообще говоря, зависит от многих факторов, в частности от того, какой тип границы рассматривается, но поскольку далее приняты очень существенные упрощения, для качественной оценки роли границ достаточно считать, что мы имеем дело со 180-градусной плоской бло-ховской границей одноосного ферромагнетика, и пользоваться выведенной для этого случая формулой [12]:

n d =

H n

H 0 + H a

2H M sinθ n =-------------n—s--------------, mw^[(^W - «2)2 + (вmw)2 ®n]1'2

где θ — угол между намагниченностью и осью анизотропии; m w — эффективная масса доменной границы; δ — толщина границы; Ω w — собственная частота ее колебаний; β — параметр затухания этих колебаний. Из (2) видно, что зависимость η ( Н 0 ) может быть сложной из-за влияния поля на Ω w , что в намагничиваемом образце практически невозможно учесть.

Степень возбуждения спиновой системы (характеризуемая, например, величиной поперечной ядерной намагниченности, которая появляется под воздействием РЧ-импульсов) не может быть просто выражена через η . Однако по условиям выполненного нами эксперимента возбуждение можно рассматривать как малое, поскольку даже в том случае, если при H 0 = 0 регистрируется наибольший возможный отклик, приложение поля его уменьшает. Показано, что в этом случае сигнал пропорционален η ² [13].

Вклад доменов и доменных границ неравноценен также вследствие разницы объемов материала, относящихся к этим состояниям. Для итоговой амплитуды, таким образом, будем полагать I e ∝ ∝ kη _d² + η _W², где k — относительный "вес" интенсивности сигнала от доменов.

Модель формирования сигнала ЯМР в магнитоупорядоченном поликристалле

В большинстве работ, посвященных ЯМР в магнетиках, считалось, что спиновая система возбуждается в доменах и доменных границах, а полный сигнал регистрируется в виде соответствующей суммы (см., например, [7]). При этом ранее в явном виде нигде не учитывалось то обстоятель- ство, что в полностью размагниченном многодоменном поликристалле некоторому выделенному объему доменов с заданной намагниченностью всегда соответствует практически равный объем с намагниченностью противоположного знака, и в них должны возникать противофазные отклики. Таким образом, сигналы от разных частей образца, не относящихся к границам, должны компенсироваться, и суммарный отклик в нулевом поле будет наблюдаться только от границ. Данное утверждение поясняется рис. 5 и подписью к нему. (Отметим, что спины в доменах возбуждаются той составляющей РЧ-магнитного поля, которая перпендикулярна намагниченности, в то время как сдвиг границ и соответственно возбуждение принадлежащих к ним ядер происходит под действием параллельной составляющей [12]). Приложение внешнего постоянного поля H0, естественно, нарушает баланс между противофазно возбужденными сигналами вследствие увеличения доли доменов с энергетически выгодным направлением намагниченности за счет тех, которые ориентированы противоположным образом.

Рассмотрение поведения ядерной спиновой системы, принявшее во внимание все указанные выше обстоятельства и примененное к образцу, содержащему множество зерен разного размера и формы, оказалось бы чрезвычайно сложным. Далее для описания среды представим ее следующим образом: пусть все кристаллиты являются одинаковыми шариками, обладающими одноосной анизотропией и разделенными на два домена противоположной ориентации. Эта структура показана

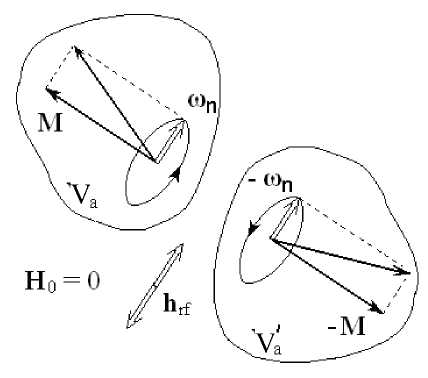
Рис. 5. Иллюстрация модели возбуждения отклика ядерной спиновой системы в областях поликристалла, ориентированных противоположным образом.

В размагниченном состоянии ( H 0 = 0 ) каждому объему материала V_a с намагниченностью М соответствует приблизительно равный объем V_a' с намагниченностью –М . РЧ-поле h rf (внутри этих объемов его действие показано в тот момент времени, когда оно максимально), отклоняя М и –М в одну и ту же сторону, вызывает в V a и V a ' противофазную прецессию ядер-ных спинов (изображено в виде разнонаправленных угловых скоростей ω n и –ω n ), т. к. сверхтонкие поля, прямо пропорциональные намагниченностям, в этих объемах антипараллельны

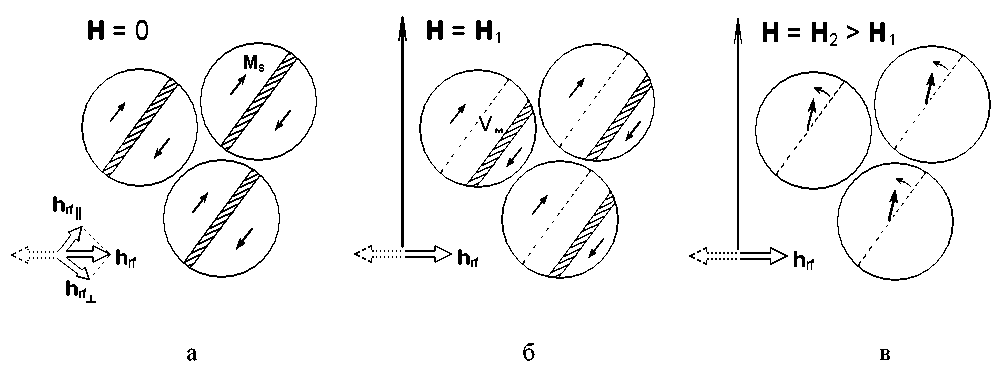
Рис. 6. Модель намагничивания поликристаллического феррита, состоящего из одинаковых сферических гра- нул, разделенных в исходном состоянии на два домена.

а — размагниченный образец, показано ориентированное в произвольном направлении РЧ-магнитное поле hrf (изображено в тот момент времени, когда оно максимально, противофазное направление — пунктир), которое раскладывается на две компоненты: параллельную, возбуждающую отклик в доменных границах (hrf║), и перпендикулярную, возбуждающую отклик в доменах hrf┴. б — образец на начальной кривой намагничивания:

к домену с выгодной ориентацией намагниченности в поле H 1 добавляется дополнительный объем V M . в — образец в состоянии насыщения, показан процесс вращения (поворот вектора M s , связан с поворотом вектора антиферромагнетизма)

на рис. 6. Будучи значительным упрощением реальной картины, такая схема все же удерживает ее основные черты и ранее успешно применялась при описании магнитных свойств ферритов [14].

На рис. 6, а, показан поликристалл в полностью размагниченном состоянии (H0 = 0), дающий сигнал только от заштрихованной области (границ). При некотором конечном H0 = H1 полный сигнал от доменов становится отличным от нуля за счет добавления к доменам выгодной ориентации дополнительного объема VМ (рис. 6, б) и начинает расти с ростом H0. Это увеличение отклика, однако, постепенно будет замедляться, т. к. коэффициент усиления, согласно (1), в доменах падает. Пока H0 < Ha, т. е. на начальных участках кривой намагничивания, изменение ηd незначительно, и сигнал от доменов должен увеличиваться. Далее фактор, связанный с коэффициентом усиления, начнет преобладать, и, пройдя через максимум, отклик от доменов станет убывающим. Объем доменных границ, как следует из рис. 6, б, с ростом H0 уменьшается все время. Как уже говорилось выше, ηw(H0) простым образом учесть нельзя, и мы вынуждены принять еще одно упрощающее предположение, в соответствии с которым полагается, что сигнал, связанный c границей, зависит только от ее объема, т. е. фактически пропорционален ее площади, т. к. толщина границы также будет считаться неизменной. В области насыщения (H0 = = H2 > HR, рис. 6, в) границы полностью исчезают, и остается только сигнал от единого домена, занимающего весь образец. Результирующая зависимость амплитуды сигнала ЯМР, представляющего собой сумму указанных откликов, от постоянного поля должна иметь немонотонный характер.

Описанная модель вступает в определенное противоречие с теми работами по нанокристалли-ческим веществам, где отклик спиновой системы наблюдался в нулевом поле. Поскольку при размере частиц меньше некоторого критического доменная структура не образуется, а ориентация намагниченностей хаотична, ЯМР в таком образце, казалось бы, не должен быть виден (отклики зерен компенсированы, границ же, которые могли бы дать в него вклад, нет). Тем не менее во многих случаях регистрировать его удается. Мы предполагаем: полная компенсация отсутствует из-за наличия дефектов. Помимо этого может существовать неоднородное распределение намагниченности внутри наночастиц, в какой-то мере играющее роль границ, т. е., таким образом, сигнал от нано– кристаллических веществ вполне может наблюдаться

Расчеты, оценки и качественное объяснение результатов

На основе предложенного подхода было выполнено вычисление коэффициентов усиления от внешнего поля. При этом было принято, что ось анизотропии кристаллитов параллельна H0, а до- бавленный за счет приложения H0 объем VM, т. е. доменнный вклад в сигнал ЯМР, пропорционален намагниченности, определяемой из эксперимента (рис. 2). Таким образом, считалось, что амплитуда той части отклика, которая связана с доменами, ниже HR описывается кривой намагничивания. Параметры последней определялись из аппроксимации, и для получения полного (выраженного в относительных единицах) сигнала было достаточно подбором определить величины На и k.

Наилучший результат был достигнут при Н а = = 200 Э и k = 700. Он показан в виде непрерывной кривой на рис. 2, имеющей максимум при том же H 0 , что и экспериментальная зависимость I e ( H 0 ) для возрастающего поля (по которому проводилась подгонка). Видно, что соответствие эксперимента и теории вполне удовлетворительно при всех H 0 .

Для обратного хода результат, к сожалению, можно назвать лишь очень приблизительным (для расчета, использующего величины, полученные из полевой зависимости эхо-сигнала и обратного хода кривой намагничивания, он изображен пунктирной линией на вставке к рис. 2). Очевидно, что здесь вступает в силу тот фактор, о котором уже говорилось выше: согласно выражению (2) коэффициент усиления в границе зависит от характеристик границы, а они при перемагничивании могут сильно измениться, т. к. граница при том же внешнем поле будет находиться в другой потенциальной яме. Данное обстоятельство подтверждается связью обратного хода I e ( H 0 ) с магнитной предысторией образца, которое иллюстрируется сравнением рис. 2 и 3.

Полученные численные оценки можно считать находящимися во вполне разумном соответствии с теми данными, которые известны для литиевого феррита. Согласно [15], в монокристалле этого соединения H a = 640 Э, что по порядку величины сходится с установленным нами значением. Величина k задает соотношение между коэффициентами усиления; из наших вычислений следует, что в доменах он меньше того, что относится к границам в k ≅ 25 раз. Если принять объем границ в десять раз меньшим объема доменов, получается, что η w ≅ 2.5 η d . Это соотношение не противоречит указанному в [1] (где в качестве возможного приводится различие на порядок). Очевидно, что ход теоретических кривых качественно также вполне соответствует экспериментальным результатам. Следовательно, при всей грубости использованной схемы, следует полагать, что в целом она верно отражает действительность.

ЗАКЛЮЧЕНИЕ

Главным результатом работы является предложение модели формирования полного сигнала ЯМР, наблюдаемого в литий-цинковом феррите и образованного из вкладов от доменов и доменных границ. На ее основе дано непротиворечивое описание поведения сигнала спинового эха в намагничиваемом материале. Подход, развитый в работе, может быть распространен на другие вещества с магнитным порядком.