Анализ поверхности оболочковой детали обшивки самолета и определение продольного формообразующего контура обтяжного пуансона с использованием Siemens NX12

В представлении поверхности оболочковой детали обшивки самолета изначально принята их привязка к обводообразующим контурам его отдельных агрегатов и самолета в целом. Это существующая технология связана с созданием аэродинамических поверхностей самолета последовательным путем построения семейств продольных и поперечных линий, принадлежащих данному объекту. Каждая линия задается множеством точек и вычисляется одним из методов одномерной интерполяции, например, с помощью сплайнов в вычислительной геометрии [1].

Набор таких линий представляет собой дискретный каркас, разбивая поверхность сложной пространственной формы на простые четырехугольные участки гомеоморфные квадрату. Квадрат автоматически покрывается сетью, а затем сеть отображается на участок поверхности. В процессе

отображения необходимо вычислять координаты, касательные и другие геометрические параметры в узловых и любых точках внутри участков. В результате реализуется заполнение участков дискретного каркаса с помощью метода двухмерной интерполяции, пока закон воспроизведения поверхности между линиями не станет доступным для воплощения при промышленном изготовлении [2].

В существующих системах геометрического моделирования необходима информация о принадлежности линий той или иной ячейке поверхности, которая задается непосредственно конструктором. Ориентация линии от начала к концу определяется последовательностью точек, которыми задана эта линия. Для характеристики таких линий поверхностей ввели понятие «характерных» контуров дискретного каркаса, которые дают представление всей поверхности, например, теоретические контура шпангоутов и стрингеров в системе координатных плоскостей самолета. В результате формируется зримый образ создаваемого аэродинамического объекта, состоящий из геометрической модели поверхности отдельного агрегата и самолета в целом [3].

Данное представление поверхностей получило развитие в методе генерации сеток как в области конечно-элементного анализа, так и в области геометрического моделирования с помощью существующих САЕ/CAD-систем широкого применения. В свою очередь, воспроизведение форм и размеров отдельных агрегатов самолета характеризуется специфичностью используемых методов и средств увязки размеров всех его сборочных элементов. Для этого существуют электронные макеты обводообразующих поверхностей агрегата самолета и оболочковых деталей обшивок в формате STEP или IGES.

Рабочая поверхность обтяжного пуансона соответствует внутренней поверхности оболочковой детали обшивки, привязанной к теоретическим контурам элементов дискретного каркаса самолета, составленных из шпангоутов и стрингеров. Для них создается базовый эталон внешних форм и размеров в виде геометрической модели агрегата, с помощью которой пытаются до сих пор заменить теоретический плаз, представляющий собой чертеж агрегата в натуральном масштабе со всеми проекциями и сечениями, позволяющими воспроизвести объемные формы и внешний контур оболочковых деталей обшивок. Поэтому поверхность оболочковой детали обшивки относится как к геометрическим объектам, так и к объектам технологической оснастки, например, к объемному шаблону контрольно-доводочной оснастки («болванка»). Эту же «болванку» используют в качестве обтяжного пуансона для процесса формообразования обтяжкой листовой оболочковой детали на специализированном растяжно-обтяжном прессе [4].

При установке «болванки» в качестве обтяжного пуансона на стол растяжно-обтяжного пресса направления стрингеров дискретного каркаса на поверхности обтяжного пуансона вдоль его длинной стороны совмещаются с боковыми кромками стола пресса, а растяжение в листе создаётся за счет усилия, приложенного к узким сторонам листовой заготовки в сегментных зажимах растяжнообтяжного пресса. При таких условиях верхний гребень обтяжного пуансона как наибольшая линия нормального сечения двухмерной поверхности, проведенное через главное касательное направление ее «вершины», соответствующее главной нормальной кривизне (продольный формообразующий контур обтяжного пуансона), имеет отклонение от стрингеровой линии дискретного каркаса и не вкладывается в вертикальную продольную плоскость симметрии растяжно-обтяжного пресса [5].

Это указывает на то, что направление растяжения при обтяжке может не совпадать с направлением прокатки листового материала. Такое положение приводит к нарушению симметрии внешней нагрузки при обтяжке с растяжением листовой заготовки, к неравномерной деформации, поперечному сдвигу тонколистового материала при формообразовании оболочковой детали обшивки по поверхности такого рода обтяжного пуансона и к гофрообразованию свободных участков листовой заготовки перед зажимами пресса.

Обозначенную производственную ситуацию можно изменить, несмотря на связанный способ агрегатной сборки самолета, выполняемый через плоские и объемные средства обеспечения геометрической увязки с линиями дискретного каркаса. Именно «болванка» является 3D объемным средством обеспечения геометрической увязки с линиями дискретного каркаса в качестве контрольно-доводочной оснастки и одновременно исполняющая роль обтяжного пуансона при формообразовании обтяжкой листовой заготовки. Для определения продольного формообразующего контура обтяжного пуансона воспользуемся специальной параметризацией поверхности, если пересечь двумя ортогональными плоскостями окрестность точки О в направлениях u и v , то в малой окрестности этой точки пересечения будут гладкими линиями i и j , которые можно считать нормальными сечениями гладкой поверхности (рисунок 1).

Такой прием получил развитие в дифференциальной геометрии, где большей частью изучаются локальные свойства поверхностей, для изучения которых достаточно рассматривать малые окрестности данной точки окрестность точки О, которая задается уравнением ƶ = f (x, y), где декартовы координаты x, y, ƶ выбираются так, что начало координат совпадает с точкой О, оси x и y лежат в ка- сательной плоскости к поверхности в точке О, а ось ƶ направлена по нормали к поверхности в точке О. Такие декартовые координаты поверхности, которые проходит через точку О, считаются репером векторов в окрестности выбранной точки [6].

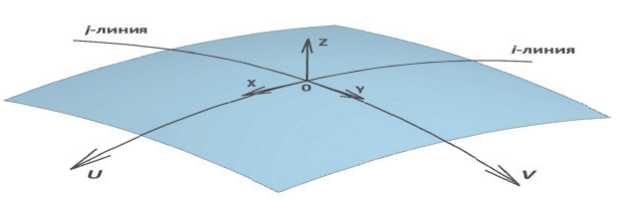
Рисунок 1 – Специальная параметризация окрестности точки О в направлениях u и v

Напомним, что для функции ƶ = f (x, y) в точке О будут выполнены равенства:

f ( О , О ) = f_х( О , О ) = f_у( О , О ) = О. Разложим функцию f (x, y) в ряд Тейлора в точке О , воспользовавшись этими равенствами, обозначим главную часть разложения через функцию Z_o(x, y):

Zo(x,y) = |(fxx( О, О )х2 +2fxy( О, О) ху+ fyy( О, О )у2). (1)

Функция Z_o (x, y) представляет собой соприкасающийся параболоид в точке О , причем первые и вторые производные функций ƶ = f (x, y) и Z_o (x, y) совпадают. Поскольку коэффициенты первой и второй квадратичных форм выражаются только через первые и вторые производные функций, задающих поверхность, то в точке О самой поверхности и соприкасающегося параболоида совпадают первая и вторая квадратичные формы, а значить и все геометрические характеристики, которые через них выражаются, в частности, у самой поверхности и соприкасающегося параболоида в точке О одни и те же нормальные кривизны по одинаковым направлениям [7].

В аналитической геометрии известно, что соответствующим поворотом осей координат x и y в касательной плоскости вокруг точки О можно уравнение параболоида привести к каноническому виду. Считаем, что согласно рисунку 1 соответствующий поворот осей координат x и y в касательной плоскости вокруг точки О уже осуществили и направления векторов репера точки О показали направления касательных к гладким линиям i и j , которые считаем нормальными сечениями поверхности. Канонический вид параболоида принимает вид:

Z o (x, y) = 2 ( k 1 X ² + k 2 y ² ) , (2)

Направления в точке О координатных осей ОX и ОY системы координат ОXY в которой уравнение соприкасающегося параболоида имеет канонический вид (2), считаются главными направлениями поверхности в точке О . Нормальные кривизны k ₁ и k₂ поверхности, вычисленные в главных направлениях, называются главными нормальными кривизнами. Таким образом, в точке О первая и вторая квадратичные формы соприкасающегося параболоида имеют соответствующий вид:

I = dx² + dy²; II = k ₁* x² + k₂* y² . (3)

Из всего сказанного следует, что в точке О на поверхности первая и вторая квадратичные формы те же самые. При этом величина К = k ₁* k₂ является инвариантом тензора кривизн линий, пересекающиеся в точке О и называется гауссовой кривизной поверхности. В зависимости от знака гауссовой кривизной точки поверхности делятся на несколько типов: эллиптическая ( К > 0), гиперболическая ( К > 0) и параболическая ( К > 0) точка поверхности. В случае на рисунке 1 К > 0, тогда в этой точке главные нормальные кривизны k ₁ и k₂ или обе положительны или обе отрицательны.

В обоих случаях соприкасающийся параболоид эллиптический. Разница лишь в том, что параболоид, касаясь плоскости x, y в своей вершине (точка О ) лежит над плоскостью, а во втором случае, касаясь той же плоскости в точке О , лежит под ней, как в случае на рисунке 1. Достаточно малая окрестность точки О на поверхности устроена как соприкасающийся параболоид. Данная точка на поверхности, в которой гауссова кривизна К > 0, является эллиптической [8]

Вводя в окрестности точки О специальную параметризацию поверхности, направим оси координат x и y по главным направлениям поверхности в точке О . Главные направления гладкой поверхности в данной точке О – это те направления, в которых нормальные кривизны достигают экстремума. Если для определенности рассматривать случай k ₁> k₂ , тогда направление оси ОX будем считать первым главным направлением. При этом на поверхности в окрестности этой точки поверхности существует ровно две главные кривизны и ровно два главных направления, которые ортогональны и являются нормальными сечениями поверхности.

Переход на новую систему координат оказался более удобным, когда имеем дело с поверхностными объектами, что согласно классической теории оболочек обеспечивает понимание симметрии формы поверхности и геометрический аспект деформации оболочковой детали. При этом геометрическую модель обтяжного пуансона необходимо строить с учётом направления прокатки листовой заготовки. Если сориентировать поверхность обтяжного пуансона относительно основной линии кривизны по продольному формообразующему контуру, направление растяжения при обтяжке листовой заготовки совпадает с направлением прокатки листа, а сам процесс проектирования твердотельного макета обтяжного пуансона выполняется в соответствующей системе вертикальных плоскостей симметрии растяжно-обтяжного пресса.

Для устранения проблемы, необходимо разработать обтяжной пуансон, который обеспечит точное соответствие его объемной формы и внешней поверхности данным калибровочной наладки при установке спроектированного обтяжного пуансона на рабочий стол растяжно-обтяжного пресса. Ключевым этапом решения этой проблемы становится определение формообразующего контура поверхности обтяжного пуансона. Требуется использование программного обеспечения CAD NX12 для проведения анализа поверхности оболочковой детали обшивки и точного вычисления положения формообразующего контура обтяжного пуансона.

• 1.    ОБОСНОВАНИЕ НЕОБХОДИМОСТИ АНАЛИЗА ПОВЕРХНОСТИ ОБОЛОЧКОВОЙ ДЕТАЛИ ОБШИВКИ В СВЯЗИ С ФОРМООБРАЗОВАНИЕМ ЛИСТОВОЙ ЗАГОТОВКИ В УСЛОВИЯХ СИММЕТРИИ

Наиболее характерным свойством данного типа деталей является то, что деталь обшивки самолета является незамкнутой оболочкой. Таким образом, срединная поверхность, толщина стенки, граничный контур и даже «вершина» оболочки как особая точка О соприкасающегося параболоида, в совокупности определяют геометрию оболочковой детали в целом.

Положение вершины (верхней точки поверхности обтяжного пуансона, точка О ) определяется, прежде всего, симметричным характером растяжения листовой заготовки влево и вправо относительно вершины и возможностью получить необходимую деформацию, соответствующую геометрии центральной части оболочки. Свойства малой области в окрестности «вершины» оболочки (точка О ) распространим только на поверхность центрального лоскута, так как не всякую поверхность можно задать целиком одним параметрическим уравнением (2). Для обсуждения локальных свойств оболочки ограничимся поверхностью центрального лоскута с касательной плоскостью к поверхности в точке О . Остальные лоскуты будут левым и правым «кусками» поверхности оболочковой детали со своей геометрией, имеющими поперечные границы с центральным лоскутом (рисунок 2).

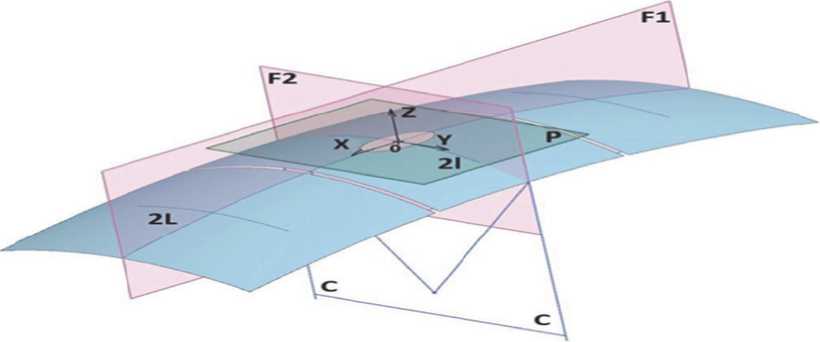
Рисунок 2 - Центральная часть поверхности оболочки двойной кривизны с касательной плоскостью в точке О на примере лоскутной модели поверхности

В рамках специальной параметризации малой области в окрестности точки О задается уравнением ƶ = f (x, y), вектора координатных осей x и y на касательной плоскости Р совмещены с направлениями главных кривизн нормальных сечений, проходящих через точку О, отображаемой как вершина поверхности оболочковой детали, имеющая касание с плоскостью. Пересечение поверхности вертикальными плоскостями F1 и F2, проходящей через нормаль z, представляет собой две плоские гладкие линии, которые можно считать нормальными сечениями поверхности. В нашем случае имеем две плоские нормальные линии, совмещенные с главными направлениями поверхности в точке О согласно рисунку 1: гладкая линия i (продольный формообразующий контур, длиной 2L) и гладкая линия j (поперечный центральный контур, длиной 2l) пересекаются в точке О .

Для практики наиболее важными элементами симметрии являются, прежде всего, касательная плоскость Р к поверхности в точке О и вертикальные плоскости симметрии F ₁ и F ₂ растяжно-обтяжного пресса, при которых два любых направления, симметричных относительно плоскостей, будут иметь одинаковые свойства. Третьим элементом симметрии являются оси симметрии, например, пара главных осей анизотропии в плоскости листового материала. Четвертым элементом являются два главных направления в касательной плоскости к поверхности оболочки в точке О . В нашем случае рассматривается эллиптическая точка О в качестве вершины поверхности обтяжного пуансона, которая является пятым элементом симметрии. Отметим, что касательная горизонтальная плоскость Р к анализируемой оболочке соответствует первоначальному положению горизонтальной листовой заготовки.

Факт совмещения направления растяжения при обтяжке с направлением прокатки листового материала подтвержден положением «правильного» эллипса, фигура которого получается при опускании вниз горизонтальной касательной плоскости к поверхности в точке О в положение секущей плоскости. Главным направлениям соответствуют главные нормальные кривизны k ₁ и k₂ , одна из которых является максимальной, а другая – минимальной по отношению к всем кривизнам плоских линий нормальных сечений, проходящих через точку О.

Для правильной ориентации рабочей поверхности пуансона, относительно горизонтально расположенной в зажимах пресса листовой заготовки, необходимо обеспечить фигуру сечения рабочей поверхности горизонтальной плоскостью в виде «правильного» эллипса. Как известно, эллипс может быть «правильным», если его продольные и поперечные полуоси попарно равны между собой. Этого можно достичь за счёт изменения положения секущей плоскости, относительно центра симметрии фигуры сечения.

Поскольку первая квадратичная форма поверхности связана с квадратом длины элемента линии на поверхности, коэффициенты этой формы остаются неизменными при изгибаниях поверхности и относятся к внутренней геометрии поверхности. Вторая квадратичная форма поверхности, в частности кривизны, показывает, в какую сторону и насколько искривлена поверхность, т.е. определяет локальное положение поверхности относительно касательной плоскости к ней, например, к точке О . Таким образом, при изучении локального строения центрального лоскута оболочки использовали тот же прием, который привел к изучению касательной плоскости.

Итак, каждая поверхность лоскута наделяется своей геометрией. Она определяется тем, как устроена в разных точках поверхности первая квадратичная форма, обеспечивающая различное изометрическое положение (изгибаемые поверхности одна на другую) открытой поверхности оболочки в целом. При этом получение изометрической формы поверхности оболочки по отношению к поверхности обтяжного пуансона приводится в условиях осевой симметрии для центрального лоскута (ось вращения с – с на рисунке 2), поперечное сечение которого является образующей поверхности вращения. Имея две изометрические поверхности, можно так изогнуть одну из них в окружающем пространстве, что она точно ляжет на вторую поверхность.

Некоторые свойства поверхности оболочки могут быть исследованы независимо от внешнего пространства. Важнейшим из этих свойств является кривизна. При этом переменная кривизна является топологическим свойством. Кривизну можно квантифицировать: для каждой точки геометрической поверхности существует число, говорящее о том, насколько изогнута поверхность вблизи этой точки. При этом, перемещая подвижный репер векторов xy z вдоль продольной кривой (формообразующий контур) влево, а потом вправо от точки О , можно изучать саму поверхность оболочки и выхватывать закономерности изменения кривизны от точки к точке, переходя с одного лоскута на другой .

Выбор системы координат в вершине поверхности обтяжного пуансона (точка О ) определяется, прежде всего, симметричным характером деформирования листовой заготовки и возможностью получить наибольшую деформацию в центральной части листовой заготовки. При формообразовании обтяжкой лучше сохранить местоположение наибольшей деформации в центральной части листовой заготовки желательно до завершения формообразования геометрической «головы», именно в окрестности вершины обтяжного пуансона.

Для этого нужно только правильно позиционировать обтяжной пуансон на столе пресса, знать траекторию движения зажимов относительно его продольного формообразующего контура и его местоположение в вертикальной плоскости симметрии обтяжного пресса, т.е. обеспечить условия для симметричной обтяжки. Настроить цикловое движение рабочих цилиндров растяжно-обтяжного пресса для конкретного процесса формообразования обтяжкой можно с учетом внутренней геометрии поверхности оболочки двойной кривизны. Выбор системы координат в вершине по- верхности обтяжного пуансона (точка О) определяется, прежде всего, симметричным характером деформирования листовой заготовки и возможностью получить наибольшую деформацию в центральной части листовой заготовки.

После вложения обтяжного пуансона на стол виртуального пресса примем плоскости F ₁ и F ₂ за вертикальные плоскости симметрии растяжно-обтяжного пресса РО-3М (рисунок 3). Примем горизонтальное положение листовой заготовки в качестве касательной плоскости к поверхности обтяжного пуансона. Обтяжной пуансон размещен на столе виртуальной модели растяжно-обтяжного пресса РО-3М, а листовая заготовка находится в зажимах пресса, установленных в горизонтальном положении, обеспечивая ее касание поверхности обтяжного пуансона в точке О .

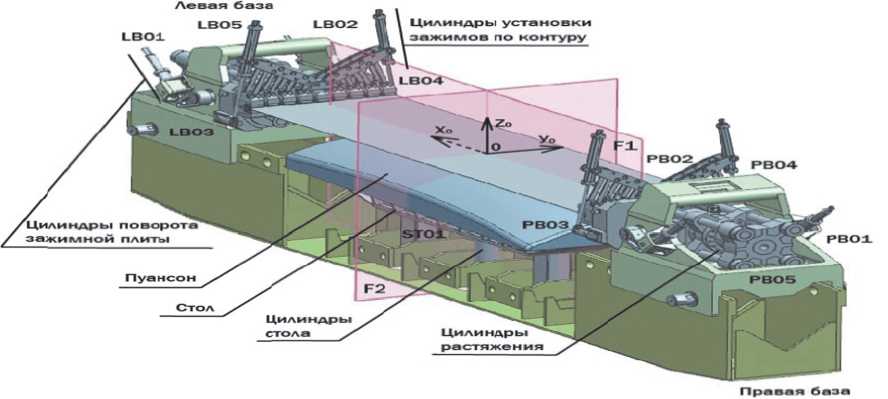
Рисунок 3 – Первоначальное положение листовой заготовки в качестве касательной плоскости к поверхности обтяжного пуансона, размещенного на столе виртуальной модели растяжно-обтяжного пресса РО-3М в системе продольной F₁ и поперечной F₂ вертикальных плоскостей симметрии пресса

Симметрия является достаточно очевидным фактом. Естественно, принципы симметрии прослеживаются в процессе формообразования обтяжкой, так и эффекты, лежащие в основе предполагаемого способа, подчиняются вполне определенным симметричным взаимосвязям с обязательным использованием программного управления, содержащего кинематические действия растяжно-обтяжного пресса. Группа симметрии формируется относительно заданного набора преобразований поверхности и сможет сыграть важную роль в совершенствовании, как теории, так и практики процесса формообразования обтяжкой тонколистовых оболочек двойной кривизны. В способе была поставлена задача, разработать такую кинематическую схему формообразования обтяжкой на растяжно-обтяжном прессе РО-3М, которая значительно уменьшила неравномерность деформации растяжения листовой заготовки. Кроме того, предполагаемый способ позволяет получить длинномерную деталь оболочки незначительной двойной кривизны за один переход [9].

Научно-обоснованный прием выполнил анализ внутренней геометрии поверхности оболочковой детали в целом, определил кривизны продольной и поперечной произвольно параметризованных кривых, ортогонально пересекающиеся в вершине обтяжного пуансона, не прибегая к натуральной параметризации, определил локальную форму поверхности в окрестности вершины обтяжного пуансона в величинах главных кривизн. При этом строили геометрическую модель обтяжного пуансона в новой системе координат с учётом направления прокатки листовой заготовки. Была сориентирована поверхность обтяжного пуансона относительно основной линии кривизны по продольному формообразующему контуру, направление которого совпало с направлением растяжения листовой заготовки, а сам процесс проектирования твердотельного макета обтяжного пуансона выполнили в соответствующей системе вертикальных плоскостей симметрии F ₁ и F ₂ растяжно-обтяжного пресса [10].

При этом сама поверхность остается инвариантной при переходе из системы координат самолета в новую систему координат, воспользовались специальной параметризацией поверхности. Геометрическая увязка сопрягаемых поверхностей деталей обшивок по обводообразующим контурам в системе основных плоскостей и координатных осей самолета не изменяется и не нарушается.

Результаты имитационного моделирования формообразующей операции обтяжки под установку на столе виртуального пресса конкретного обтяжного пуансона показывают то, что можно обе- спечить изготовление оболочковой детали в соответствии требованиям по качеству (допустимое равномерное утонение, точную геометрическую форму и отсутствие ручных доводочных работ). Этот вывод подтвержден при верификационной отработке обтяжкой оболочковой детали при установке обтяжного пуансона в симметричное положение на столе растяжно-обтяжного прессе РО-3М, вложив продольный формообразующий контур обтяжного пуансона в вертикальную плоскость симметрии F1 растяжно-обтяжного пресса. На настоящий момент проанализировали большую группу оболочковых деталей обшивок и пришли к выводу, что проще изготовить новые обтяжные пуансоны, чем дорабатывать существующие «болванки».

Для анализа геометрии поверхности оболочковой детали обшивки и для построения обтяжного пуансона использовалась программа Siemens NX12, которая предоставляет мощные инструменты и позволяет с высокой точностью определять продольный формообразующий контур поверхности обтяжного пуансона. Этот процесс играет важную роль в производстве оболочковых деталей, где критически важны точность, качество поверхностей и соответствие геометрическим требованиям.

2.    АНАЛИЗ ГЕОМЕТРИИ ПОВЕРХНОСТИ ОБОЛОЧКОВОЙ ДЕТАЛИ ОБШИВКИ И ОБТЯЖНОГО ПУАНСОНА

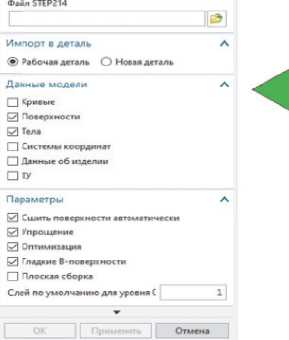
Программа Siemens NX12 предоставляет мощные инструменты для анализа поверхности оболочковых деталей обшивки. Для начала работы необходимо либо импортировать модель оболочковой детали, либо создать ее геометрию непосредственно в программе NX12. Импорт осуществляется через стандартные форматы CAD-файлов, такие как STEP, IGES или Parasolid. В случае создания модели с нуля проектировщик может воспользоваться инструментами программы для построения исходной геометрии: скелетных линий, профилей, сплайнов и поверхностей. На этом этапе важно добиться максимального соответствия созданной геометрии исходным техническим требованиям, так как от этого зависит точность последующего анализа. Процесс импортирования 3D модели в программную среду NX12 показан на рисунке 4.

Одной из ключевых задач анализа является выделение и построение формообразующего контура оболочковой детали. Такие контуры формируются на основе пересечений поверхностей с нормальной вертикальной плоскостью. NX12 предоставляет целый спектр инструментов для работы с геометрией поверхности, включая функции Surface Analysis (Анализ поверхностей), Curve Creation (Создание кривых) и Section Extraction (Извлечение сечений). Эти инструменты помогают проектировщику точно определить границы и характеристики обвода, что крайне важно для последующего производства или симуляции. Но для начало необходимо создать и проанализировать поверхность обтяжного пуансона, для этого необходимо применить инструмент «Расширить». На рисунке 5 показан результат предварительного продления рабочей поверхности обтяжного пуансона, «припа-совыванием» ее к внутренней поверхности оболочковой детали. Это необходимо для более точного анализа геометрии оболочковой детали.

Рисунок 4 - Процесс импортирования 3D модели оболочковой детали обшивки в программу NX12

Импорт из

О Импортировать

В результате выполнения операции продления поверхности в программном обеспечении NX12, была получена поверхность, выделенная серым цветом, как показано на рисунке 6. Данная поверхность характеризуется отсутствием вырезов, что существенно упрощает процесс ее анализа и дальнейшего моделирования обтяжного пуансона.

Поверхность без вырезов предоставляет более целостное и единообразное поле для проведения анализа поверхности. Это способствует улучшению точности моделирования и повышает эффективность процесса создания обтяжного пуансона. Такие поверхности значительно упрощают последующие этапы проектирования и оптимизации, позволяя сосредоточиться на более детальном и глубоком анализе основных геометрических характеристик.

Кроме того, отсутствие вырезов на расширенной поверхности способствует минимизации потенциальных ошибок и недочетов, связанных с нестыковками и несовпадениями на границах вырезов. Для того, чтобы решить эту проблему, нужно произвести отрисовку сплошной поверхности детали обшивки без краевых вырезов элементов, получаемая формообразованием обтяжкой из листовой заготовки.

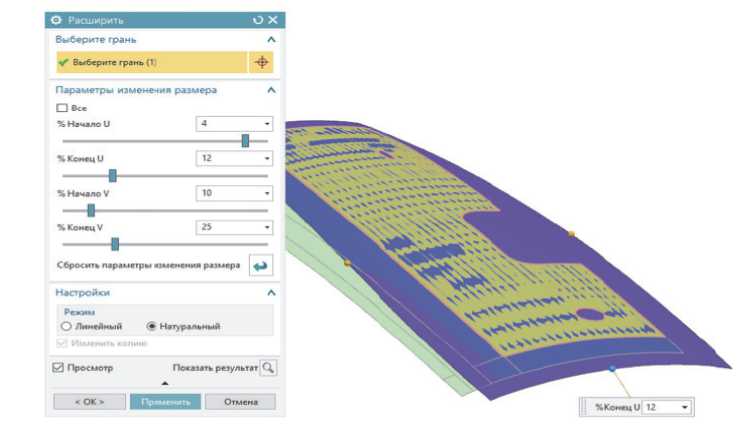
Рисунок 5 - Предварительное продление поверхности обтяжного пуансона при помощи инструмента «Расширить»

Рисунок 6 - Отрисовка сплошной поверхности детали обшивки без краевых вырезов и внутренних элементов поверхности оболочковой детали обшивки

После выполнения поверхности обтяжного пуансона в рамках процесса детализации и обеспечения её функциональной точности проводится построение продольной и поперечной линий, исходящих от краев поверхности. Эти линии являются основой для дальнейшего построения касательной плоскости, которая, в свою очередь, используется как плоскость основания обтяжного пуансона.

Процесс определения этой плоскости критически важен для точного построения геометрической модели обтяжного пуансона с учётом направления прокатки листовой заготовки. Для проверки корректности выбранной плоскости она поднимается до вершины поверхности пуансона в положение касательной плоскости. На следующем этапе выполняется операция погружения касательной плоскости в положение секущей плоскости, обеспечивая вырез фигуры в форме эллипса вблизи вершины поверхности обтяжного пуансона, как показано на рисунке 7.

После получения эллипсной фигуры на поверхности обтяжного пуансона важным шагом является анализ и корректировка его положения относительно вершины поверхности. Эллипс должен иметь одинаковые полуоси от всех своих сторон до вершины поверхности, что критически важно

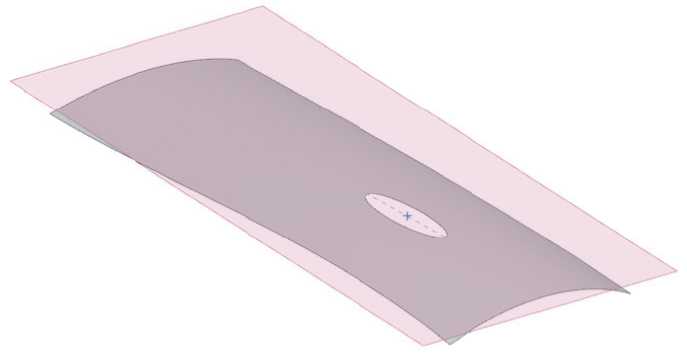
Рисунок 7 - Касательная плоскость к вершине поверхности в положении секущей плоскости

для обеспечения симметрии положения поверхности обтяжного пуансона. Определив направление большой оси эллипса, проходящей через центр его симметрии, получили направление главной кривизны рабочей поверхности пуансона, как показано на рисунке 8.

Если при первичном построении обнаруживается, что полуоси эллипса имеют различные расстояния относительно вершины, это свидетельствует о некорректности выбора плоскости. В таком случае рекомендуется адаптивное изменение положения плоскости, чтобы эллипс приобрел ровное и симметричное расположение относительно вершины поверхности обтяжного пуансона. Достижение этих условий способствует построению ортогональных линий главных кривизн на поверхности обтяжного пуансона, как показано на рисунке 9.

После достижения необходимого результата, секущую плоскость совместно с рабочей поверхностью обтяжного пуансона необходимо развернуть вокруг точки О так, чтобы направление оси эллипса совпало с направлением прокатки заготовки. Кроме этого, необходимо обеспечить равными большие и малые полуоси счет качания секущей плоскости в двух направлениях.

Выбор системы координат в вершине поверхности обтяжного пуансона (точка О ) определяется, прежде всего, симметричным характером деформирования листовой заготовки и возможностью получить наибольшую деформацию в центральной части листовой заготовки.

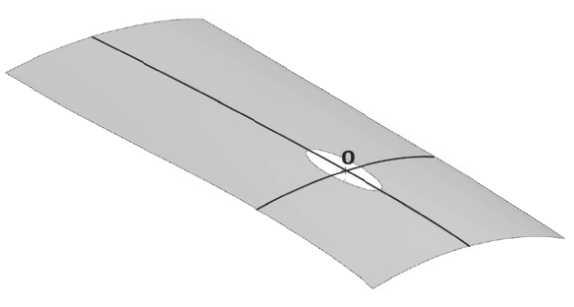
Рисунок 9 - Построение ортогональной пары линий главных кривизн поверхности

Рисунок 8 - Определение большой оси эллипса относительно точки О

Продлим одну сторону поверхности обтяжного пуансона, обеспечивая центральное положение точки О , как показано на рисунке 10. В результате оба контура пересекаются в «вершине» (точка О ) поверхности оболочки двойной кривизны и переходят в вертикальные плоскости симметрии растяжно-обтяжного пресса F₁ и F₂ согласно рисунку 3. Внешне процесс симметричной обтяжки напоминает формообразование и заключается в том, что плоская листовая заготовка превращается в пространственную оболочковую деталь под воздействием растягивающих усилий, расположенных с двух узких противоположных концов в направлении прокатки листовой заготовки (симметрия анизотропии).

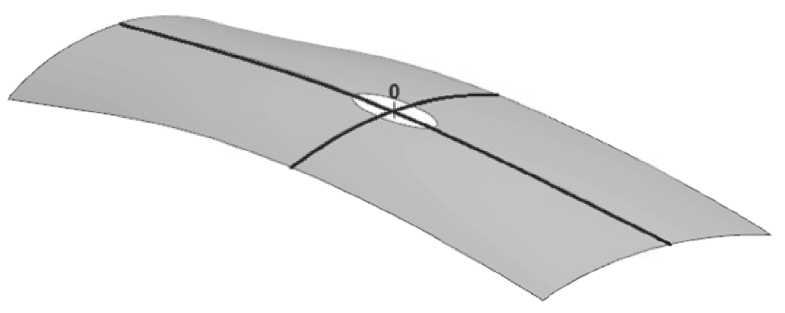
Рисунок 10 - Формирование полной поверхности обтяжного пуансона за счет перемещения точки О в центральную часть поверхности обтяжного пуансона

На рисунке 11 представлены поверхность обтяжного пуансона и размещённая на ней оболочковая деталь обшивки.

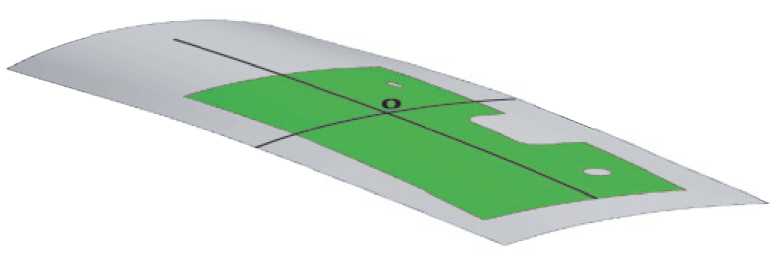
Рисунок 11 - Положение контура оболочковой детали обшивки на поверхности обтяжного пуансона

Следующим шагом необходимо создать стенки и основание модели обтяжного пуансона, уделяя особое внимание геометрическим параметрам, как показано на рисунке 12. Важнейшим аспектом данного этапа является формирование радиусных переходов на краях поверхности обтяжного пуансона. Результатом всех вышеописанных этапов проектирования является готовый пуансон. Он представлен в визуализированном виде на рисунке 10. Установка данного обтяжного пуансона в симметричное положение на столе растяжно-обтяжного прессе РО-3М, вложив формообразующий продольный контур обтяжного пуансона в вертикальную продольную плоскость симметрии растяжно-обтяжного пресса, сможет решить обозначенную производственную ситуацию по решению проблемы, несмотря на связанный способ агрегатной сборки самолета через средства обеспечения геометрической увязки с линиями дискретного каркаса.

Таким образом, по готовой 3D геометрической модели фрагмента обшивки (поверхностного обвода) самолёта технолог сможет «напрямую» построить геометрическую модель поверхности обтяжного пуансона пресса с учётом направления прокатки листовой заготовки и ориентируемости поверхности обтяжного пуансона относительно основной линии кривизны по продольному формообразующему контуру, направление которого совпадает с направлением растяжения при обтяжке.

Рисунок 12 - Твердотельная модель обтяжного пуансона

Такое совпадение обеспечивает контроль симметричного развития очага деформации, и преимущественного образования зоны пластической деформации в центральной части листовой заго- товки. В результате решаются проблемы формообразования обтяжкой оболочковых деталей обшивок, что приводит к равномерному изменению толщины в различных областях листовой заготовки и к возможности изготавливать оболочковые детали обшивки самолётов без гофрообразования.

3.    КРИТЕРИАЛЬНАЯ РАСЧЕТНАЯ ВЕРИФИКАЦИЯ ГОФРООБРАЗОВАНИЯ ПОВЕРХНОСТИ ОБОЛОЧКОВОЙ ДЕТАЛИ В ОБЛАСТИ СЕКЦИОННЫХ ЗАЖИМОВ ПРЕССА

Для прогнозирования гофрообразования листовой заготовки в процессе формообразования обтяжкой по «болванке» была построена FLD диаграмма. Данные для диаграммы предельного формообразования были получены путем испытаний образцов по методике Накадзимы. Поведение листовой заготовки в процессе формообразования зависит от нескольких факторов ; важность каждого из этих факторов зависит от используемого процесса. Эти факторы включают кривую напряжения деформации, анизотропию, неоднородность листа и чувствительность к деформации [11]. FLD - это диапазон комбинаций деформаций, которые определяют начало образования гофр [12]. Для использования FLD на практике вместо кривой рассматривается доверительная область. Таким образом, если распределение деформаций во всех точках листа ниже FLD, лист вытягивается без разрыва, если комбинация деформаций в критической области детали выше FLD, действительно будут гофры, и операция формообразования останется незавершенной. На рисунках 13 и 14 представлена палитра распределения участков FLD диаграммы на листовой заготовке в процессе формообразования обтяжкой по «болванке».

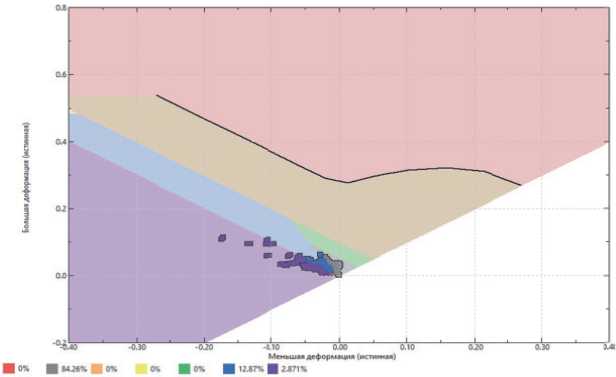
Рисунок 13 - FLD диаграммы на листовой заготовке в процессе формообразования обтяжкой по «болванке»

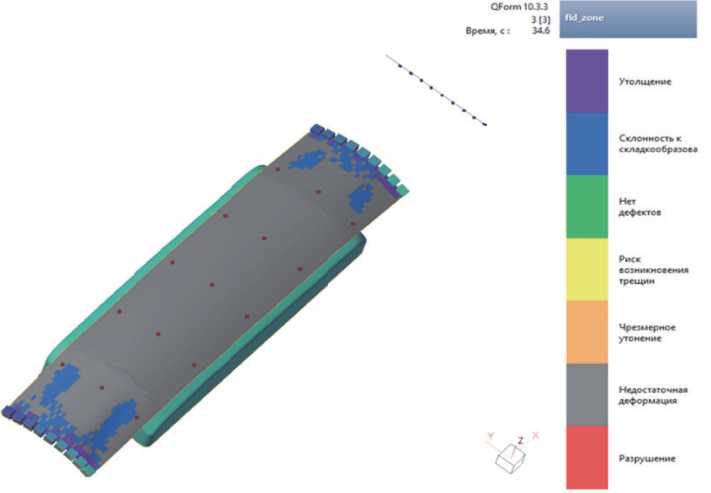
Рисунок 14 - FLD диаграммы на листовой заготовке в процессе формообразования обтяжкой по «болванке»

Согласно результатам моделирования и построенной FLD диаграмме на свободных участках листовой заготовки присутствуют зоны, составляющие 12,8% от всей площади, подверженные склонности к складкообразованию.

На рисунках 15 и 16 представлена палитра распределения участков FLD диаграммы на листовой заготовке в процессе формообразования обтяжкой, построенной на принципах симметрии.

Согласно результатам моделирования и построенной FLD диаграмме на свободных участках листовой заготовки присутствуют зоны, составляющие 6,53% от всей площади, подверженные склонности к складкообразованию.

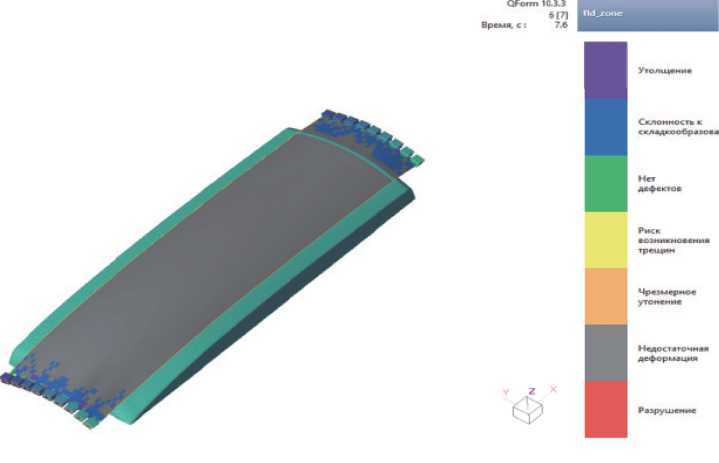
Рисунок 16 - FLD диаграммы на листовой заготовке в процессе формообразования обтяжкой, построенной на принципах симметрии

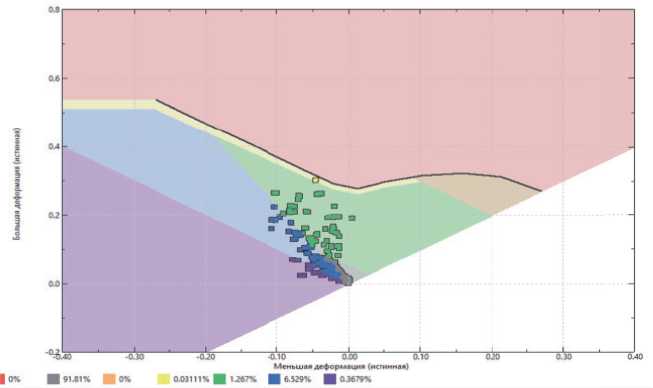
Рисунок 15 - FLD диаграммы на листовой заготовке в процессе формообразования обтяжкой, построенной на прин ципах симметр ии

Область листовой заготовки в зажимных устройствах, не подверженная дефектам составляет 1,27%. Из диаграммы видно, что область заготовки, которая подвержена образованию складок, находится на свободных концах и не стремится распространиться в область пуансона, что показывает отсутствие риска распространения складки в области зоны детали. Такая работа была направлена на повышения технологических возможностей процесса формообразования обтяжкой, что приводит к равномерному изменению толщины в различных областях листовой заготовки и к возможности изготавливать оболочковые детали обшивки самолётов без гофрообразования.

ЗАКЛЮЧЕНИЕ

Чтобы изготавливать оболочковые детали обшивки самолётов без гофрообразования в пределах допусков по равномерности пластической деформации (утонению) нужно располагать геометри- ей рабочей поверхности обтяжного пуансона. Кроме того, необходимо правильно сориентировать рабочую поверхность пуансона по отношению к продольному формообразующему контуру. Такой прием позволяет произвести формирование поверхности оболочковой детали обшивки и геометрии рабочей поверхности обтяжного пуансона в системе двойной кривизны оболочки, характеризуемой двумя ортогональными линиями кривизны и имеющие начало координат в точке касания горизонтальной плоскости листовой заготовки с вершиной поверхности обтяжного пуансона.

Были учтены кинематика растяжно-обтяжного пресса РО-3М и начальное положение листовой заготовки; описан порядок определения места очага пластической деформации заготовки («вершины») и направления главных кривизн. Листовая заготовка располагается горизонтально (в зажимах пресса), направление прокатки листа перпендикулярно зажимам пресса и совпадает с продольным направлением растяжения. Направление главной кривизны поверхности обтяжного пуансона лежит в плоскости направления прокатки листовой заготовки.

В ходе выполнения работы был проведен детальный анализ и реализован метод геометрического моделирования рабочей поверхности обтяжного пуансона с использованием программного пакета Siemens NX 12, пригодный для практического использования технологами предприятия, что позволил определить базовые принципы и получить геометрические параметры, необходимые для дальнейшего формирования 3D-моделей обтяжного пуансона. На основании полученной геометрии была успешно построена опорная плоскость, которая является основой для формирования подошвы обтяжного пуансона. В результате разработана и визуализирована твердотельная модель обтяжного пуансона с рабочей поверхностью, продольный формообразующий контур которого совмещен с направлением прокатки листовой заготовки.

Проведенные в рамках работы исследования включали не только геометрический анализ и моделирование, но и расчет процесса обтяжки в программе QForm с применением разработанного пуансона. Полученные результаты расчетов подтвердили эффективность способа формообразования обтяжкой и показали положительные итоги использования нового обтяжного пуансона. Это доказывает, что спроектированный обтяжной пуансон соответствует проектным требованиям и готов для внедрения на производственных этапах.

Достигнутые результаты подтверждают корректность выбранной подхода проектирования и её пригодность для разработки обтяжных пуансонов взамен «болванок». В результате, выполненный анализ способствует повышению качества изготовления оболочковых элементов самолётов. Предстоящие изменения в технологии формообразования обтяжкой позволяют решить проблемы за счет изменения схем формообразования обтяжкой и устранения ограничивающих факторов, влияющих на деформуемость листовых заготовок, особенно из алюминиевых сплавов из-за повышенной склонности гофрообразованию.