Анализ прибыли предприятия на основе математического моделирования

В обстоятельствах рыночных отношений повышаются значение и роль анализа финансового состояния предприятия, которое несет полную экономическую ответственность за последствия производственнохозяйственной деятельности перед акционерами, работниками, банками и кредиторами.

Прибыль является конечным финансовым результатом, который характеризует производственно-хозяйственную деятельность предприятия, что является основой для экономического развития предприятия. Рост прибыли формирует финансовую основу для самофинансирования деятельности предприятия, за счет которой реализовывается часть обязательств перед бюджетом, банками и другими предприятиями [1, С. 118]. Таким образом, прибыль занимает центральную позицию для оценки производственной и финансовой деятельности предприятия, она характеризует сметы его деловой активности и финансовое благополучие [7, С. 70].

Цель анализа заключается не только в том, чтобы установить и оценить финансовое состояние предприятия, но и в том, чтобы непрерывно его улучшать. Анализ выявляет направлении и позиции в финансовом состоянии предприятия. Анализ отвечает на вопрос, каковы способы улучшения финансового состояния предприятия в конкретный период [3, С. 3]. Своевременность устранения недостатков и нахождение резервов улучшения. Для проведения оценки устойчивости финансового состояния предприятия применяется система показателей, характеризующих изменения:  структуры капитала предприятия по его размещению к источникам образования; эффективности и интенсивности его использования; платёжеспособности и кредитоспособности предприятия; запаса его финансовой устойчивости.

Главной целью финансового анализа является получение ключевых параметров, которые дают полную картину финансового состояния предприятия, его прибылей и убытков; изменений в структуре активов и пассивов, в расчётах с дебиторами и кредиторами [4, С. 30].

На сегодняшний день, математико-статистические исследования являются необходимым инструментом для получения глубоких и полноценных знаний. Объективно существующие зависимости и взаимосвязи между экономическими явлениями большей частью описаны только вербально. Значительно важнее количественно измерить тесноту причинно-следственных связей и выявить форму влияний [6, С. 38]. Для исследования интенсивности, вида и формы причинных влияний широко применяе нужных результатов.

Множественный корреляционно-регрессионный анализ финансовой устойчивости проведён по данным предприятия ООО «Гелий». В качестве результативного показателя (Y) была принята чистая прибыль. Прибыль – это важнейший показатель эффективности и результативности предприятия. Она является главной целью деятельности предприятия и необходима для дальнейшего его развития.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Применительно к множественной регрессии, необходимо до определения вида модели, произвести отбор факторов [8, С. 83]. Факторы, включаемые в модель должны быть:

• 1.    количественно измеримы (если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность);

• 2.    факторы не должны быть интеркоррелированы (корреляция независимых переменных в регрессионных моделях) и тем более находиться в точной функциональной связи (каждому возможному значению показателя-фактора х соответствует одно или несколько строго определенных значений результативного показателя [2, 115]. Это может привести к тому, что система уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии (если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения оказываются не интерпретируемыми) [9, С. 52].

В качестве показателей-факторов, потенциально влияющих на значение прибыли, использованы ключевые финансовые величины. Среди них выделены: х1 – выручка от реализации, х2 – всего затраты на реализованную продукцию, х3 – текущий налог на прибыль, х4 – прибыль от продаж, х5 – основные средства, х6 – готовая продукция и товары, х7 – денежные средства, х8 – прочие оборотные активы, х9 – кредиторская задолженность.

Проведение многомерных статистических исследований, в частности регрессионного анализа, невозможно без массовых наблюдений. В связи с этим в результате обработки годовых отчётов ООО «Гелий» за 8 лет был сформирован исходный массив для анализа информации (табл. 1).

Таблица 1

Исходная информация для проведения корреляционно-регрессионного анализа ООО «Гелий»

Перио д	Y	х1	х2	х3	х4	х5	х6	х7	х8	х9
2001	755 231	4 815	3 670	290 451	1 145	2 238	205	16 922	222	323
		415	104		311	021	343		698	097
2002	-148 299	4 431	4 205	42 279	226 157	2 295	318	28 968	286	529
		726	569			258	485		709	718
2003	62 805	5 011	4 656	27 097	354 887	2 157	129	2 122	350	891
		211	324			195	960		589	381
2004	236 880	5 694	4 990	138 590	704 335	2 155	132	9 685	238	790
		583	248			582	843		464	995
2005	576 453	6 768	5 767	252 492	1 000	2 070	113	21 482	228	490
		274	941		333	236	017		077	029
2006	692 385	7 437	6 446	246 706	990 767	2 157	92 722	134 761	215	720
		270	503			388			566	204
2007	2 876	9 764	7 091	624 763	2 673	2 272	116	1 965	165	337
	791	217	113		104	718	377	773	094	017
2008	1 639	10 562	8 086	634 560	2 476	2 445	279	583 971	447	428
	463	959	628		331	180	499		657	276

Наиболее простой формой зависимости и достаточно строго обоснованной для случая совместного нормального распределения является линейная, то есть зависимость вида:

y = a0 +a1*x1 +a2*x2 +…+aР*xР                           (1)

Следует определить, все ли переменные нужно включать в уравнение, или есть переменные, которые существенно не влияют на величину Y и их нецелесообразно включать в уравнение (1).

Для решения этого была рассчитана таблица, составленная из коэффициентов парной корреляции для всех 9 факторов (табл. 2).

Таблица 2.

Таблица коэффициентов парной корреляции.

	Y	х1	х2	х3	х4	х5	х6	х7	х8	х9
Y	1
х1	0,84716 4	1
х2	0,71552 6	0,97167 2	1
х3	0,93109 4	0,91743 2	0,80128 4	1
х4	0,95806 1	0,91922 6	0,80013 4	0,99353 1	1
х5	0,43475	0,50117	0,42240	0,58495	0,56827	1

	5	6	7	8
х6	0,15593	0,07575	0,10887	0,03491 3	-0,01087	0,75457 5	1
х7	0,93463 1	0,72080 2	0,60404	0,76911 1	0,47564 9	0,38692 4	0,14406	1
х8	0,17375	0,18413 8	0,25364 9	0,06320 3	0,04476 8	0,56691 1	0,56736 4	-0,25271	1
х9	0,61869	0,39462	0,21711	-0,68103	-0,63985	-0,48272	0,36153	-0,49809	0,18043 7	1

На основании данных, полученных в таблице, можно сделать вывод, что связь факторов х1, х2, х3, х4, х7, х8, х9 с фактором Y существенная (коэффициенты корреляции равны соответственно (0,85; 0,72; 0,93; 0,96; 0,93; 0,62).

Величина коэффициента корреляции колеблется в пределах: ^{-1 ≤ r yx ≤ 1} и показывает силу связи, которую можно определить по шкале Чеддока (табл. 3):

Таблица 3.

Шкала Чеддока.

Величина r yx	Характер связи
До 0,1	Слабая
0,3-0,5	Умеренная
0,5-0,7	Заметная
0,7-0,9	Высокая
0,9-0,99	Весьма высокая

Применим метод последовательного исключения объясняющих переменных (стоит упомянуть, что из двух объясняющих переменных, имеющих высокий коэффициент корреляции одну переменную исключают из рассмотрения, при этом какую переменную оставить, а какую удалить из анализа, решают в первую очередь на основании экономических соображений; если же в этом направлении ни одной из переменных нельзя отдать предпочтение, то оставляют ту из двух, которая имеет больший коэффициент корреляции с зависимой (объясняемой) переменной) [5, 308]:

• -    факторы х2, х5, х6, х8, х9 исключаются в первую очередь, так как имеют низкий коэффициент корреляции (<0,75);

• -    находим максимальный элемент (0,99) и сравниваем коэффициенты r ,r              r ≥ r

корреляции ^{yx 4 yx 3} , так как ^{yx 4    yx 3} , исключаем х3;

• -    находим максимальный элемент (0,919) и сравниваем r ,r              r ≥ r

коэффициенты корреляции ^{yx 1 yx 3} , так как ^{yx 3    yx 1} , исключаем х1;

• -    остались показатели, уровень значимости, которых больше 0,75.

Из данной модели исключаются факторы х1, х2, х3, х5, х6, х8, х9. Таким образом, уравнение регрессии приобрело вид:

y = a0 +a1*x4 +a2*x7                                         (2)

После предварительного отбора факторов на основе парных и частных коэффициентов корреляции была произведена оценка параметров а0, а1, а2 по методу наименьших квадратов. Уравнение регрессии приобрело вид:

Y = -149972,4+0,6355187*X4 +0,6544871*X7 (3)

Для определения тесноты связи между фактором Y и совокупностью факторов X4, X7 был применён коэффициент множественной корреляции R. Коэффициент изменяется в интервале от 0 до 1. Если R = 0, то нет линейной корреляционной связи между Y и X4, X7. Если R = 1, то существует функциональная связь. В представленном случае R = 0,99, что говорит о наличии функциональной связи. Обычно интерпретируется не сам коэффициент корреляции R, а его квадрат R , который называется коэффициентом множественной (общей) детерминации. Он показывает, какая часть общей дисперсии объясняется за счёт вариации линейной комбинации аргументов х4, х7 при данных значениях коэффициентов регрессии. В представленном случае R = 0,984029, то есть 98% вариации результативного признака объясняется факторами, включёнными в уравнение регрессии.

Для более подробного анализа требуется рассчитать средний коэффициент эластичности, который показывает, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины, для этого используем формулу 4.

Эх ) = 1

Где у(х) - значение функции у при среднем значении факторной переменной х; ai - коэффициент регрессии; x - среднее значение факторной переменной х.

Найденные коэффициенты эластичности E4(Y) = 0,908989 и E7(Y) = 0,270304, показывают, что увеличение прибыли от продаж на 1% приведёт к увеличению чистой прибыли в среднем на 0,91%. Увеличение денежных средств на 1% приведёт в среднем к увеличению чистой прибыли на 0,27%.

На рисунке 1 показана динамика изменения чистой прибыли по уравнению регрессии (4).

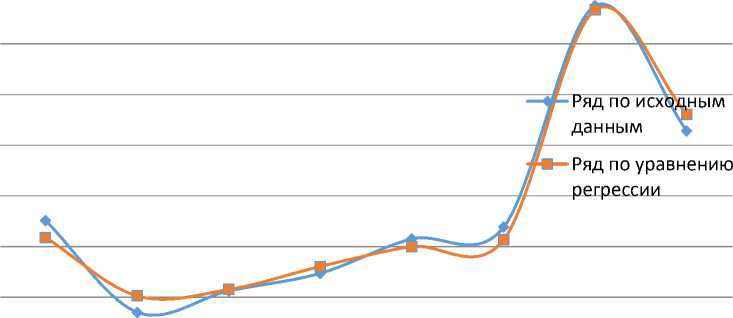
Рис. 1. динамика изменения чистой прибыли по уравнению регрессии.

Интерпретация уравнения регрессии будет следующей. За рассматриваемый период (8 лет) в ООО «Гелий» при увеличении прибыли от продаж на единицу от своего 0,6544871 . «R = 0,98» среднего уровня чистая прибыль увеличится в среднем на 0,6355187 единиц; при увеличении денежных средств на единицу от своего среднего уровня результативный показатель увеличится в среднем на 0,6544871 единиц. Коэффициент «R2 = 0,98» показывает, что 98% вариации результативного признака объясняется включёнными в модель факторами (прибылью от продаж и денежными средствами). Таким образом, руководству ООО «Гелий» необходимо обратить внимание на данные факторные признаки, поскольку управление ими способно оказать значительное влияние на величину чистой прибыли.