Анализ применения треугольника линейных токов и напряжений для селекции повреждений в электрических системах

За последнее десятилетие в релейной защите произошли качественные изменения, вызванные широким использованием микропроцессорной (цифровой) техники. Использование микропроцессорной техники дает существенные возможности в реализации традиционных способов селекции повреждений в электрических системах, однако новые возможности цифровой обработки сигналов и обмена информацией позволяют реализовать и новые способы селекции, которые невозможно было осуществить ранее. Вследствие этого появляется возможность повышения эффективности и надежности функционирования релейной защиты, а значит, и электрических систем в целом.

В данной работе рассмотрены векторные диаграммы и возможность применения изменения треугольника междуфазных токов и напряжений для фиксации возникновения коротких замыканий.

В нормальном устойчивом режиме работы трехфазной электрической сети векторные диаграммы токов и напряжений симметричные и уравновешенные. То есть фазные векторы токов и напряжений в любой момент времени образуют равносторонний треугольник междуфазных напряжений и токов (рис.1).

Рис. 1. Векторная диаграмма и треугольник линейных напряжений

В данном случае U A = U B = U C = U Ф , углы между фазными векторами равны, исходя из этого площадь треугольника линейных напряжений можно определить, используя известную формулу площади для равностороннего треугольника:

S u = -4- • ( U ab ) 2 ,                                    (1)

где S_U - площадь треугольника линейных напряжений, U_AB – линейное напряжение.

Известно, что в симметричном режиме:

U л = V- • U ф , где UЛ – линейное напряжение, UФ – фазное напряжение сети.

Тогда площадь можно определить по формуле:

3 ⋅

SU = 3 4 3 ⋅ UФ2 .(2)

Аналогично находится и площадь треугольника линейных токов.

3⋅V3 , 2_

SI = 3 4 3 ⋅IФ2 .(3)

При возникновении несимметрии в сети искажаются треугольники линейных токов и напряжений. Это явление можно использовать для селекции несимметрии в сети. На рисунке 2 показано, как искажается треугольник токов при появлении несимметрии I ₂ = 0,5 ⋅ I ₁ , a = 30 ^o , где a – угол сдвига между токами прямой и обратной последовательности. При появлении тока обратной последовательности площадь треугольника линейных токов уменьшается по отношению к площади нормального режима, причем изменение площади пропорционально квадрату величины тока обратной последовательности [1].

∆ S = ^{3 73} ⋅ I ² .                                            (4)

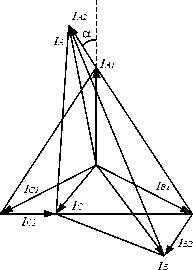
Рис.2. Изменение треугольника линейных токов при появлении несимметрии

Справедливо данное доказательство и для напряжений; изменение площади треугольника линейных напряжений:

∆ S = ³ ₄ ³ ⋅ U 2² .                                           (5)

Рассмотрим данное явление применительно к конкретным видам повреждений, для этого построим векторные диаграммы, характеризующие начальный момент короткого замыкания на линии с односторонним питанием при отсутствии нагрузки [2].

Трехфазное короткое замыкание . Симметричное трехфазное КЗ – наиболее простой для расчета и анализа вид повреждения. Он характерен тем, что токи и напряжения всех фаз равны по значению как в месте КЗ, так и в любой другой точке сети:

I = I = I ; U = U = U .

AB C A B C

Напряжения всех фаз при данном виде повреждения в месте КЗ равны нулю, площадь искаженного треугольника равняется нулю, следовательно, изменение площади максимально и определяется по выражению:

3 ⋅ 3        2 3 ⋅ 3        3 ⋅

∆ S U = S UN - S UK 3 = ³ ₄ ³ ⋅ U Ф ² - ³ ₄ ³ ⋅ 0 = ³ ₄ ³ ⋅ U Ф ² ,                    (6)

где S_UN - площадь треугольника линейных напряжений нормального режима, S_{UK 3} - площадь треугольника линейных напряжений при трехфазном коротком замыкании.

Кроме того, токи во всех фазах при КЗ значительно возрастают, а площадь треугольника линейных токов возрастает.

Двухфазное короткое замыкание. Векторная диаграмма при двухфазном КЗ показана на рисунке 3.

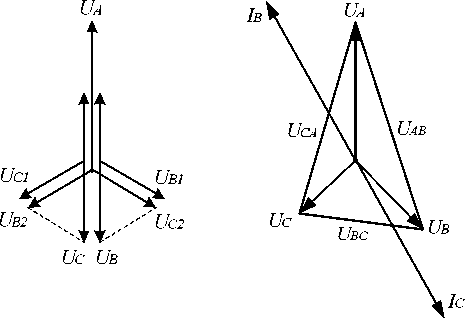
а                              б

Рис. 3. Векторная диаграмма: а - напряжений при двухфазном КЗ в месте повреждения; б - напряжений и токов по мере удаления от точки КЗ

Допустим, замыкание произошло между фазами B и C. Токи в поврежденных фазах равны по значению, но противоположны по фазе, а ток неповрежденной фазы равен нулю.

Ia = 0; Ib = Ic

Таким образом, при двухфазном КЗ площадь треугольника линейных токов равна нулю, т.к. треугольник междуфазных токов превращается в линию, это демонстрирует векторная диаграмма (рис. 3 б). Изменение площади A S I максимально, равняется площади треугольника линейных токов нормального режима.

Напряжение неповрежденной фазы А одинаково в любой точки сети. Поскольку междуфазное напряжение в точке КЗ U_BC = U _B - U_C равно нулю, то U_B = U_C , т.е. фазные напряжения равны по модулю и совпадают по фазе. В месте КЗ напряжение каждой поврежденной фазы равно половине напряжения неповрежденной фазы и противоположно ему по знаку:

Ub = Uc =— UA ■

Как видно из векторной диаграммы, площадь треугольника линейных напряжений в месте КЗ тоже равняется нулю, изменение площади максимально и равно площади треугольника нормального режима.

По мере удаления от точки КЗ напряжение U_BC несколько возрастает, это обусловлено уменьшением напряжения обратной последовательности, изменение площади A S U уменьшается.

Однофазное короткое замыкание. Замыкание одной фазы на землю вызывает появление тока только в электрических сетях 110 кВ и выше, работающих с глухозаземленной нейтралью. Векторная диаграмма при однофазном КЗ показана на рисунке 4.

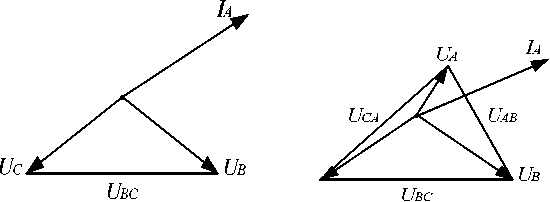
Рис.4 Векторная диаграмма токов и напряжений при однофазном КЗ: а - в месте повреждения; б - напряжений и токов по мере удаления от точки КЗ

При замыкании фазы А токи в неповрежденных фазах равняются нулю I_B = I_C = 0 . Треугольник линейных токов, также как и при двухфазном КЗ, превращается в линию. Площадь треугольника токов равна нулю, и изменение площади ∆ S_I максимально.

Напряжение поврежденной фазы А в точке КЗ равно нулю U _A = 0 . Наряжения неповрежденных фаз В и С равны э.д.с. этих фаз. Площадь треугольника напряжений при данном виде КЗ в точке повреждения не равна нулю, но уменьшается относительно площади нормального режима. По мере удаления от точки КЗ площадь треугольника несколько возрастает. Несмотря на то, что площадь не равна нулю, её изменение имеет место.

Из вышесказанного следует, что при коротких замыканиях происходит искажение треугольника токов и напряжений и, соответственно, его площади.

На рисунке 4 показана зависимость изменения площади треугольника линейных напряжений от напряжения фазы А. Данная зависимость построена с помощью Microsoft Excel по реальным данным осциллограмм регистратора аварийных событий «Черный ящик», при трехфазном коротком замыкании на воздушной линии напряжением 220 кВ.

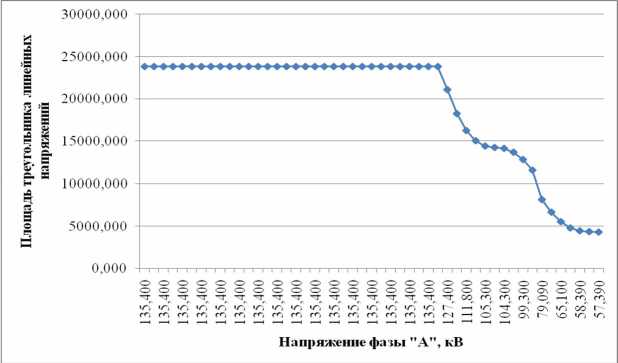
Рис. 5 Зависимость площади треугольника линейных напряжений от напряжения фазы А при трехфазном КЗ на линии

График, изображенный на рисунке 5, наглядно подтверждает приведенные выше теоретические выводы. Как видно, нормальный режим работы характеризует прямолинейный участок графика, а режим трехфазного КЗ нисходящий участок. Подобную картину можно наблюдать и на рисунке 6, где показана зависимость изменения площади треугольника линейных токов от тока фазы А. В отличие от изменения площади напряжений площадь треугольника токов при трехфазном КЗ увеличивается.

Таким образом, выявить КЗ возможно по изменению площадей треугольников напряжений и токов.

Данный метод основан на определении площадей треугольников напряжений и токов по формуле Герона:

S=VP⋅(P-AB)⋅(P-BC)⋅(P-AC),(7)

где P – полупериметр треугольника;

AB , BC , AC – стороны треугольника, определяемые по теореме косинусов (обобщенной теореме Пифагора):

AB2 =BC2 +AC2 -2⋅BC⋅AC⋅cosa.(8)

На основании формул (7) и (8) получили: например, для напряжений:

SU = VPU⋅(PU-UAB)⋅(PU-UBC)⋅(PU-UAB);(9)

стороны тр еугольника напряжен ий:

UAB= U2A+UB2-2⋅UA⋅UB⋅cos(=a),UBC UB2+UC2-2⋅UB⋅UC⋅cos(=β), UAC U2A+UC2-2⋅UA⋅UC⋅cos(γ) ;(10)

полупериметр:

р _ UAB + UBC ^{+ U}AC

PU =        2

uA + UB"2 ' UAUB'cos( a ) |+[ TB + UC~2 ' UB^UC'^ в ) |+| ^A + UC~2^VAUC " c^ ^Y )

площадь треугольника напряжений:

PJ 1 PU 4UA + UB - 2'UA UB ■^cos< “ ) J'l PU 4UB + Uc "2 ' UB ^UC '^cos ( в ) I'l PU — ^ A ⁺ Uc — 2UA UC 'cos( Y )

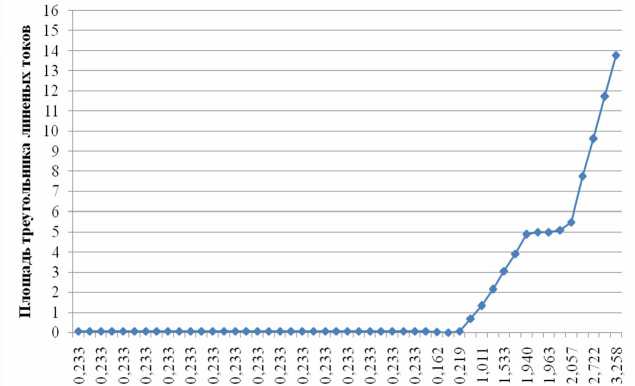
Ток фазы "A", kA

Рис. 6. Зависимость площади треугольника линейных токов от напряжения фазы А при трехфазном КЗ на линии

В условиях современного развития цифровой техники релейной защиты появилась возможность векторного отображения дискретизированных синусоидальных сигналов. При этом синусоидально изменяющемуся сигналу x ( t ) = A • sin( ^ ₀ 1 + ф ) соответствует вектор x ( t ) = A • e^j ' ^{( m 0} t ^+ф ) , равномерно вращающийся с угловой частотой го 0 против часовой стрелки. Проекция этого вектора в любой момент времени на ось ординат соответствует мгновенному значению сигнала x ( t ) . На сегодняшний день разработаны различные алгоритмы вычисления векторов на основе мгновенных значений [3].

Полученные векторы можно использовать и для вычисления площади треугольника линейных напряжений или токов в любой момент времени по формуле (7). По изменению найденных площадей появляется возможность фиксации возникновения коротких замыканий, следовательно, и создания измерительного органа релейной защиты.