Анализ процедур моделирования и описания процессов проектирования организации производства

Неупорядоченность производства и его подсистем в виде технико-экономического проектирования (САПРТЭП) приводит его математическую модель вида [1]:

P ( t ) = [ P op ( t ) + P t ( t ) ] • С (1)

к вероятностному виду

P ( t ) = [ MP ( t ) + MP t ( t ) + P op ( t ) + P t ( t ) ] ■ С ,(2)

P op ( t ) и P t ( t ) —

где

компоненты характерис-

тик, значения которых определяются организа- ционными и технологическими процессами в САПРТЭП; t – некоторая независимая переменная; MP op (t) и MPt (t) – компоненты математического ожидания данного параметра, определяемые этими же процессами; С – стоимостные показатели (или стоимость функции управления процессами).

В зависимости от выбранной модели, САП-РТЭП подразделяются на три класса:

• 1.    Производственно-технологические:

• 2.    Организационные:

• 3.    Технико-экономические:

Pt (t ) = MPt (t) + Pop (t);

Pop (t ) = MPop (t)+ Pt (t);

P (t) = MPop (t) + MPt (t) + Pop (t) + Pt (t)■

Засканов Виктор Гаврилович, доктор технических наук, профессор, заведующий кафедрой организации производства.

При совершенствовании системы любого класса априори необходимо найти лишь одну из функций MP_t ( t ) или MP op ( t ) . Для этого можно использовать два способа:

априорный , когда вид зависимости MP_t ( t ) и MP op ( t ) выбирают, исходя из некоторых теоретических исследований и анализа предполагаемого к созданию объекта, где еще имеется возможность устранения возмущений (ошибок);

апостериорный, когда MP T (t) и MPop (t) определяют экспериментально по результатам математической или электронной модели на натурном образце, когда уже исправить или устранить ошибки (возмущения) – невозможно. В любом случае предполагается, что для исследуемого объекта выполняется соотношение

MP(t) = [MPop(t)+ Pt(t)]■ Ci. (3)

Для технико-экономических процессов в САПРТЭП, не имеющих точного детерминированного математического описания, задача построения математической модели процесса (технико-экономического процесса) сводится в основном к нахождению функции MP _t ( t ) и реже Pt ( t ) ■

Таким образом, для исследования и математического описания САПРТЭП как промышленной системы, используем методологию функционально стоимостной инженерии и рассмотрим ряд вопросов, связанных с построением математических моделей этой системы.

АНАЛИЗ ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ ОПИСАНИЯ СИСТЕМ

ПРОЕКТИРОВАНИЯ

Метод планирования эксперимента. Для многофакторных процессов, математическая модель которых соответствует зависимости MP T ( t ) = MP T ( t 1 , 1 2 ,..., t n ) , статистическую взаимосвязанность факторов можно определить методами математического планирования эксперимента. Различают три типа эксперимента:

• активный – искусственно изменяется ход технико-экономического процесса с целью получить его математическую модель;

• пассивный – устанавливается связь между технико-экономическими факторами по результатам наблюдений за самопроизвольными изменениями технико-экономического процесса;

• 2 .

смешанный (активно-пассивный) – часть управляемых факторов изменяют по своему желанию, а остальные изменяются самопроизвольно.

При построении математических моделей технико-экономического процесса в САПРТЭП, если из теоретических соображений о процессе нельзя сделать заключение о характере взаимосвязи между переменными, математическую модель их взаимосвязанности выбирают априори. Аналогичной задачей корреляционного и регрессионного анализа в качестве таких моделей используются полиномы первой и второй степеней. В частности для двух переменных факторов эти полиномы могут иметь вид y = a 0 + a 1 x1 + a 2 x 2;

y = a ₀ + a 1 x 1 + a ₂ x ₂ + a ₁₂ x 1 x ₂ + a 11 x 1 + a ₂₂ x

2 f (4)

Нелинейность взаимосвязи технико-экономических и факторов производства приводит к тому, что нелинейная модель (4) имеет малую адекватность для области изменения техникоэкономических и факторов производства, применяется для описания малых областей факторов пространства, в которых нелинейными зависимостями можно пренебречь.

Чтобы упростить запись и обработку результатов, полученных при проведении активного эксперимента , масштабы переменных выбирают так, чтобы верхний уровень фактора соответствовал (+1), нижний (– 1), основной – (0). Для натуральных непрерывных переменных это требование нормировки выполняется путем преобразования абсолютных значений технико-экономических факторов x_i в относительные x_j :

• ^xj = ^{( x}i ^{— x}i 0 ⁾ / I i ,

где x_i0 – основной уровень переменной, относительно которого ведется ее варьирование; I_i – интервал варьирования.

На практике опытного производства различают два вида активного эксперимента: полный факторный и дробный факторный .

При полном факторном эксперименте реализуются все возможные сочетания уровней. Число опытов N для получения оценки состояния технико-экономического и производственного процессов в промышленных АСУ при этом равно N = 2 ^k , где k – число варьируемых переменных.

В частности, для трех переменных необходимо провести восемь опытов по матрице планирования (табл. 1).

Таблица 1. Матрица планирования для трех переменных (8 опытов)

Нмер опыта	x1	х2	x3	y
1	+1	-1	-1	1
2	-1	+1	-1	2
3	-1	-1	+1	3
4	+1	+1	-1	4
5	+1	-1	+1	5
6	-1	+1	+1	6
7	+1	+1	+1	7
8	-1	-1	-1	8

Значения y₁ – y₈ оптимизируемого техникоэкономического фактора y при активном трехфакторном эксперименте соответствуют его значениям в вершинах куба факторного пространства (области существования технико-экономического процесса). По результатам полного факторного эксперимента находят коэффициенты аппроксимирующего полинома (4)

N

• ai = E yjxij / N,          (5)

i = 1

где i – номер фактора ( i = 0, 1, 2, …).

Фактор x_i при i = 0 называется фиктивным фактором и вводится для удобства вычисления коэффициента a₀ , входящего в математическую модель технико-экономического процесса (4). При введении фиктивного фактора в математическую модель технико-экономического процесса модель будет иметь следующий вид:

y = f (xo, xi, x2,..., xn ).        (6)

При полном факторном эксперименте появ- ляется возможность учесть без увеличения числа опытов взаимодействие технико-экономических факторов. В этом случае математическая модель технико-экономического процесса (6) примет вид:

У = a 0 x 0

+ a 1 x1

+ a 2 x 2 + a

12 ^x 1 ^x 2 .

Коэффициент a_i в выражении (7) вычисляется по формуле (4), а коэффициент a_mi :

N

a = E У ixm, I N,       (8)

i = 1

где m и i – номера факторов ( m, i = 1, 2,…, k при m ^ i ).

Методы вариационного исчисления. Этот метод применяется в тех случаях, когда ставятся задачи оптимизации управления по априорным математическим и электронным моделям, и он сводится к определению неизвестных функций y(x) , обеспечивающих экстремум определенных интегралов вида

^x 2

I = J Fyi (x), y2 (x), -y. (x); y 'i (x), y '2 (x), - - -,y' n (x);x ] dx, (9) xi где n = 1, 2,…, N.

Известно, что вариация дy функции y(x), переменного x, есть функция от x , определяемая при каждом значении x как разность новой функции V(x) и функции y(x) : дy = V(x) – y(x) .

Вариация дy , вызывая изменение функциональных связей между x и y , приводит к изменению функции F [ y 1 ( x ) , y 2 ( x ) ,..., y n ( x ) x ] . Приращение 8F , соответствующее вариациям 8 1 , 8 ₂,-.., 8 n , определяется следующим выражением:

AF = F(y 1 + 8yx; y 2 + 8 2;

; У п ^{+ 8 y} n ; ^{x )-}

- F(y 1, y 2,---, Уп ; x)

Если функции y(x) и д(x) дифференцируемые, то вариация производной y(x) есть

8y ’ = 8 dy-dx

d dx

(8y)= V'(x)-y'(x). (11)

Необходимым, но недостаточным условием экстремума функционала:

V = 2 N N - j

N     E0 N (N + 1) ,       (12)

где j = n_N – 1 , является

^x 2

8=j8Fdx= x1

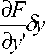
x2 - xfd fdF) [ J dx ^ dy' J x1 x1L \ y /

dF

dy

8ydx = 0(13)

для произвольно малой величины дy .

Основная задача оптимальных систем, решаемая методами вариационного исчисления [2],

состоит в нахождении такой функции управления, которая минимизировала бы функционал (9) при следующих условиях:

• 1.    Закрепленными граничными точками.

• 2.    Подвижными в граничных точках.

• 3.    Минимуме отклонения выходной переменной от заданного значения.

Вариационные задачи при перечисленных условиях в большинстве случаев решаются численными методами дифференциальных уравнений. Тем не менее, ряд практически важных результатов можно получить и аналитически.

Задача нахождения минимума функционала при закрепленных конечных точках tk

I = J F (y,y',t) dt (14)

t0

интерпретируется как нахождение оптимальной траектории движения объекта, обеспечивающей минимум отклонения скорости y’ от заданной.

Экстремум функционала I находится из решения дифференциального уравнения, соответствующего обращению в нуль вариации функционала

dE I dy -(d I dt)(dFI dy ') = 0. (15)

Уравнение (15), определяющее оптимальную траекторию y(t) , является дифференциальным уравнением Эйлера-Лагранжа и может в ряде случаев решаться аналитически.

Задача нахождения минимума функционала при подвижных конечных точках (одна или обе точки перемещаются) обязательно имеет решение в случаях, если функционал (15) минимизируется при неподвижных конечных точках. Класс функций, удовлетворяющих минимуму функционала, расширяется, так как положение конечных точек не фиксировано. Задача нахождения минимума функционала при условии минимума отклонения выходной переменной от заданного значения сводится к решению следующего уравнения:

( F' yq x ' - Fxq 'y )/ q' x - ( d/dx )( Fx /q' x ) = 0 ,(16) где F ' _y , q ' _x , q ' _y — частные производные d F I d y , d q I d x и d q I d y .

Задачу решают для объектов и систем уравнений, которые описываются функцией У ' ( t ⁾= q ( y , x ) при начальных условиях y ( t ₀ ) = y ₀ . Оптимальную функцию управления y(t) находят из уравнения (16) численными методами. Использовать методы вариационного исчисления для анализа и оптимизации технико-экономических процессов управления не всегда эффективно из-за относительной сложности учета ограничений, налагаемых на изменение переменных, а также из-за необходи-

мости решать автоматизированным способом (либо на ПЭВМ) двухточечные краевые задачи, требующие значительных затрат памяти и машинного времени.

Следует отметить, что для анализа техникоэкономических решений при описании САПР-ТЭП могут использоваться и другие методы анализа классической высшей математики как: принцип максимума, метод динамического программирования, градиентные методы и др.

На основании вышеизложенного, анализ технико-экономических методов описания систем проектирования процессов организации производства заключается в нахождении минимума функционала при подвижных конечных точках, когда обязательно находится решение в ситуациях, где функционал dE/dY-(d/dt)(dF/dy')=0 минимизируется при неподвижных конечных точках и класс функций расширяется при минимуме функционала, а положение качественных точек не фиксировано.