Анализ процесса движения нити при ее сматывании с паковок швейных и трикотажных машин

В современных моделях высокоскоростных швейных и трикотажных машин актуальной задачей является выравнивание скорости и натяжение колебаний нитей, возникающих в результате цикличного движения рабочих органов. Особое внимание требуется уделять при работе с нитями, имеющими латексный сердечник, в которых могут накапливаться значительные упругие и остаточные деформации. Чем выше производительность оборудования, тем больше неравномерность структуры текстильного изделия из-за колебания натяжения нитей при сматывании её с паковки, и, соответственно, образования брака. Нерешенным является вопрос определения влияния конструктивных параметров швейных и трикотажных машин на характер колебания скорости нитей [1-3].

Сматывание нити рассмотрено в работе [4] применительно к трикотажным машинам. В работе [5] изложены элементы процесса затягивания стежка в швейных машинах, относящиеся, в основном, к проведению петли нити внутрь сшиваемых материалов. Меньше всего изучены явления, связанные с движением нити при сматывании её с паковки (катушки). Вместе с тем, изучение характера движения нити на этом участке позволяет не только лучше представить весь процесс работы механизмов и узлов швейной машины, но и также определить влияние физико-механических свойств применяемых нитей на стабильность технологического процесса в целом [6-7].

Определение параметров движения нити при сматывании ее с паковки приобретает особенно большое значение при проектировании устройств, контролирующих длину нити. От характера и качественных характеристик движения нити в этот период зависит точность работы формирующих устройств и степень влияния их на работу оборудования в целом.

Целью настоящей работы было исследование движения отрезка нитки, расположенного между бобиной и регулятором натяжения машины.

Задачей исследования являлось определение математических зависимостей колебаний натяжения и скорости нити при циклическом движении механизмов швейной машины, что является актуальным. Использовались методы математического моделирования и положения теории механизмов и машин.

ОСНОВНАЯ ЧАСТЬ

Методика проведения исследований изучения колебаний натяжения и соответственно скорости основывается на аналитических методах теории механизмов и машин. Изучение конструкции оборудования позволило получить исходные данные для моделирования процесса сложного движения нити. При исследовании принималось во внимание не только растяжение нити и наличие переходных процессов трения в регуляторе натяжения, как это было сделано в работе [8], но и трение нитки об ушко нитепри-тягивателя.

Переходя от реальной механической системы к её физической модели, упрощаем систему и пренебрегаем изгибом нити в регуляторе натяжения, деформацией контура нити, и другими факторами, которые в данной частной задаче представляются несущественными. При дальнейших расчётах принимаем также, что нить является весомой, абсолютно гибкой и при растяжении подчиняется закону Гука [9].

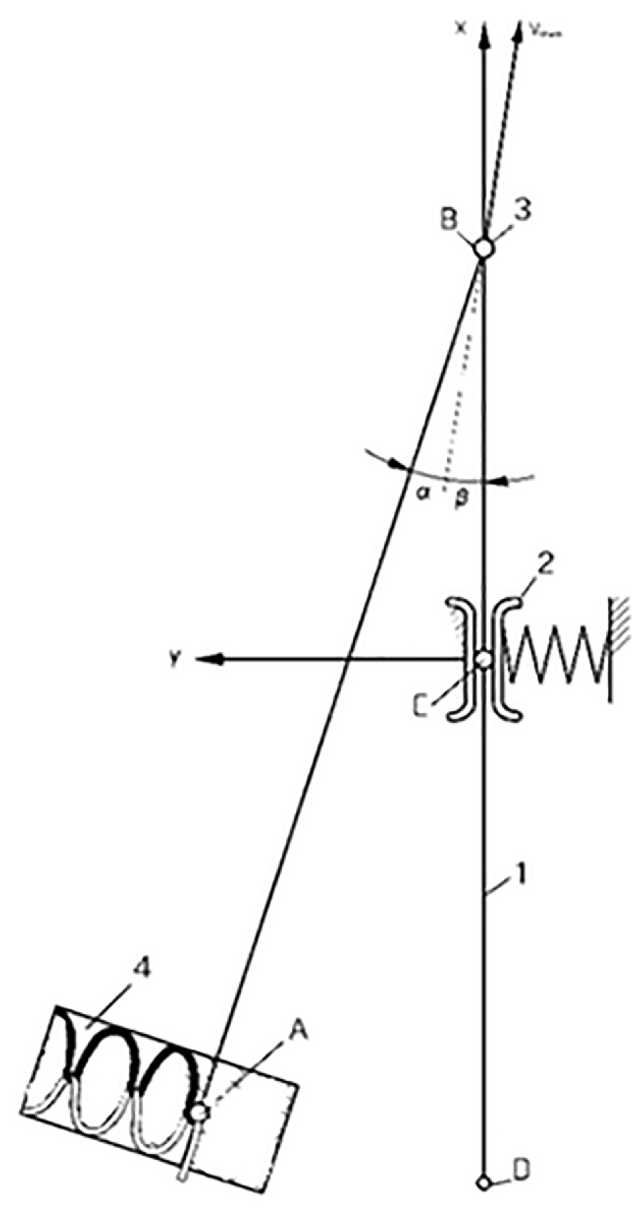
На расчетной схеме (рис. 1) изображена нить от места ее переплетения в стежке (точка А) до места сматывания с бобины (точка D). Всю длину нитки условно делим на отрезки АВ, ВС и CD. Во время движения отрезка СD на него действует сила T_BC (t) , равная натяжению отрезка ВС, и сила трения в регуляторе натяжения. Усилием сопротивления разматыванию нитки на бобине пренебрегаем. Для характеристики переходного процесса трения нитки о детали регулятора натяжения принимаем закон Кулона [10], учитывающий разницу между силой трения покоя R₁ и постоянной по величине силой трения движения R₂ . Принимаем, что сила R₁ уменьшается до силы R₂ мгновенно. Такая упрощённая характеристика трения, вероятно, отличается от реального закона, но хорошо согласуется с общепринятыми взглядами на процесс образования челночных стежков и достаточна для анализа главных особенностей исследуемого движения. Теоретические исследования проводим с использованием положений теории механизмов и машин [11].

В момент окончания затягивания стежка точка А нитки останавливается. В этот момент, который принимаем за начало отсчета времени (t = 0) , перемещение х отрезка СD и его начальная скорость ẋ равны нулю, то есть:

X (0) = 0, x (0) = 0 (1)

В начальный момент натяжение отрезка BC равно T_BC(0) = R₁ , а его деформация

δlBC (0) = R1l0BC / EF (2)

где l⁰_BC - длина отрезка BC до деформирования; E - модуль упругости нити; F - площадь поперечного сечения нити.

Натяжение T_AB(0) отрезка AB в начальный момент определим, полагая, что нить охватывает ушко ните-притягивателя по дуге окружности.

Тогда T_AB(0) определяется натяжением растянутой нити [5]:

При этом деформация отрезка AB

δl_AB (0) = R₁ e^-μΘ l⁰_AB / EF              (5)

где l⁰_AB - длина отрезка AB до деформации.

К текущему моменту времени t деформация отрезков AB и BC изменится и составит соответственно δl_AB (t) и δl_BC (t) . Выразим полную деформацию контура ABC нитки в текущий момент времени в виде суммы приращений деформаций, образующихся на каждой условной ступени общего процесса нагружения нити:

δl AB (t) + δl BC (t) =

= δlAB (0) + δlBC (0) + δlABC (h) - x,

где δl_ABC (h) - деформация контура нити, вызванная движением ушка нитепритягивателя.

Представим выражение для деформаций через усилия в явном виде:

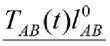
EF

TbcWbc EF

= ^^ + ^ + ^^-Х

Воспользовавшись формулой Эйлера T_AB (t) = T_BC (t)e ^-μΘ и проделав преобразования, получим выражение для натяжения отрезка BC в текущий момент времени:

T_BC (t) = R₁ + cδl_ABC (h) - cx, (8)

1 – нить, 2 – регулятор натяжения,

3 – ушко нитепритягивателя, 4 – зона стежка

1 – thread, 2 – tension regulator,

3 – eyelet of the thread stretcher, 4 – stich zone

Рисунок 1 – Расчетная схемаFigure 1 – Calculation scheme

где

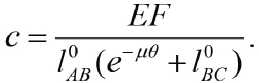
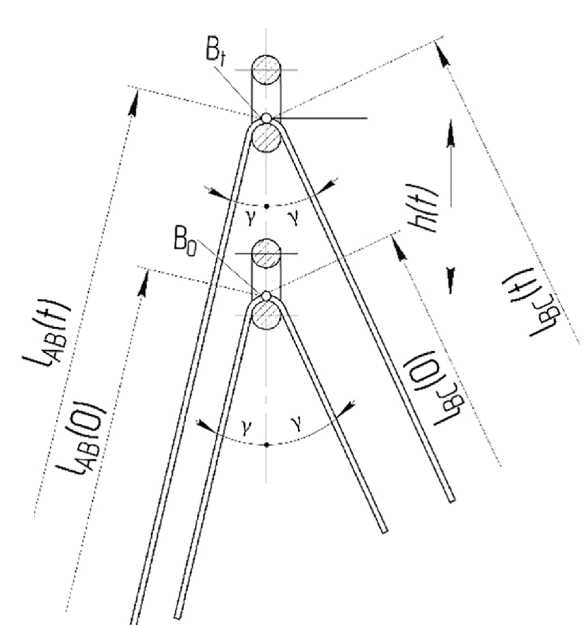
Для определения функции δl_ABC (h) сделаем некоторые допущения. Учитывая, что длины отрезков AB и BC значительно больше величины перемещения ушка нитепритягивателя в период сматывания, будем считать, что эти отрезки располагаются под постоянным углом γ = (α + β) /2 (рис. 2) к траектории ушка, движение которого в этот период принимаем равномерно замедленным, то есть:

T_AB (0) = T_BC (0)e^-μΘ            (3)

Ю=^-?Е

где μ - коэффициент трения нитки об ушко нитепри-тягивателя; Θ - угол охвата ушка нитепритягивателя растянутой нитью, или

T_AB (0) = R₁e^-μΘ               (4)

где ϑ₀ – скорость ушка нитепритягивателя в начальный момент сматывания; а – ускорение ушка в период сматывания.

Тогда, пренебрегая деформацией незначительных

по величине криволинейных участков нити, огибающих ушко, имеем: 2 (10) Подставив полученное выражение в уравнение (2), получим: 2 (11) Q      V /                      \ Рисунок 2 – Схема для определения деформации контура нити, вызываемой перемещением ушка нитепритягивателя Figure 2 – Diagram for determining the deformation of the thread contour caused by the movement of the eyelet of the thread stretcher С учётом полученных выражений дифференциальное уравнение движения отрезка CD имеет вид 2 (12) или (13) 2          m k2 = c / m, где m – масса отрезка CD. Решение этого уравнения, отвечающее начальным условиям (1), равно х = 2ϑ0 cos γ - (2a cos γ) t - (14) - 2ϑ0 cos γ cos kt + Ak sin kt,

где m Уравнение решаем при следующих условиях E = 2 × 105 (H/см2); F = 4,16 × 10-4 см2; μ = 0,15; θ = 1,87; l0AB = 0,22 м; l0ВС = 0,1 м; R1 = 2,4 H; R2 = 2,3 H; а = 7º; β = 8º Графики перемещения и скорости отрезка CD для хлопчатобумажной нитки № 50/3, длиной 100 см, при различных скоростях швейной машины и расходе, показаны соответственно на рисунке 3. 8__________________________ 3 6---- ? ^7^--- 1  2~/>^ 2 —V/ ---- 0                          ------ 43    50 S3 60    63 cp« а (a) /dr------------------------------ 12----- °4S SO 5S 60    63 tp« б (b) 1 – 1000 об/мин; 2 – 2000 об/мин; 3 – 3000 об/мин. φ – угол поворота главного вала машины 1 – 1000 rpm; 2 – 2000 rpm; 3 – 3000 rpm φ – rotation angle of the machine main shaft Рисунок 3 – Графики перемещения (а) и скорости (б) отрезка CD нити при различных скоростях главного вала машины, об/мин Figure 3 – Graphs of movement (a) and speed (b) of the CD thread segment at different speeds of the main shaft of the machine, rpm

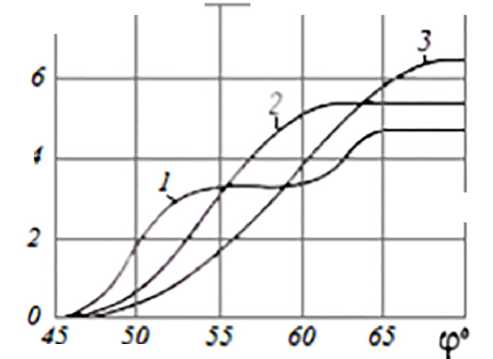
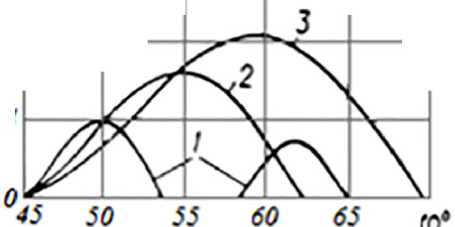
Как видно, процесс перемещения отрезка носит разрывной автоколебательный характер. Чем меньше скорость машины и жёсткость нитки, тем более выражен процесс автоколебаний: отрезок движется периодически, с остановками. Расчёты показывают, что длина нитки, сматывающейся с бобины в течение одного цикла работы нитепритягивателя, может быть больше необходимой для образования стежка. Поэтому во время работы машины следует ожидать, что величина сматывающейся с бобины нитки для каждого цикла образования стежка будет различной.

Для практической проверки полученных результатов на ООО «Сиба» г. Санкт-Петербург прибором для измерения скорости вращения и линейной скорости нитей TESTO-471 на модернизированной швейной машине Textima были замерены скорости сматывания нитки с бобины при частоте главного вала машины, об/мин; 1 – 1000 об/мин; 2 – 2000 об/мин; 3 – 3000 об/мин.

Отмечено:

• 1.    Мгновенная скорость движения нитки согласуется с теоретическими исследованиями.

• 2.    Средняя скорость движения нитки соответствует паспортным данным швейной машины.

• 3.    Присутствуют значительные колебания мгновенной скорости движения нитки при сматывании ее с паковки.

ЗАКЛЮЧЕНИЕ

Проведены аналитические и практические исследования движения участка нитки при сматывании ее с бобины. Установлено, что скорость движения нити является переменной величиной, что влияет на процесс образования петли. Предложенные теоретические исследования позволяют определить скорость и натяжение нитки в процессе сматывания с бобины, рассчитать критические режимы работы оборудования. Практическая проверка в производственных условиях показала соответствие полученных результатов предложенной методике расчета.