Анализ процесса идентификации параметров морфометрии рек и водохранилищ в компьютерных моделях гидравлических расчетов (результативность и однозначность калибровки)
Автор: Левит-Гуревич Леонид Константинович, Никифоров Дмитрий Андреевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Водные ресурсы
Статья в выпуске: 6-1 т.17, 2015 года.
Бесплатный доступ
Компьютерные модели гидравлических расчетов водохранилищ и участков рек предназначены для постоянной по запросам эксплуатации в инженерных и управленческих целях, оценки гидрологических явлений и пр. При подготовке компьютерных гидравлических моделей возникает необходимость их калибровки - корректировки первоначально заданных параметров морфометрии водного объекта с целью приближения результатов расчетов, полученных в определенных гидрологических условиях, к наблюденным фактически данным при этих условиях - уровням на створах наблюдений, а также к установленным характеристикам водохранилищ. Рассмотрен процесс калибровки по шагам. Доказано, что процесс калибровки однозначно приводит к искомой цифровой модели изучаемого участка реки.
Река, гидравлический расчет, компьютерная программа, цифровая гидравлическая модель, калибровка
Короткий адрес: https://sciup.org/148204205
IDR: 148204205 | УДК: 556.536:681.3
Process identification analysis of morphometry parameters of rivers and reservoirs in computer models of hydraulic calculations (effectiveness and uniqueness of calibration)
Computer models of hydraulic calculations of water reservoirs and river sections are designed for continuous operation at the request in engineering and management purposes, evaluation of hydrological phenomena and so forth. In the preparation of hydraulic computer models there is a need of calibration, adjustment to the original set parameters morphometry of the water body in order to bring the results of calculations obtained in certain hydrological conditions, according to the observations of fact, under these conditions, levels of cross-sections for observation and to established characteristics of reservoirs. The process of calibration steps. It is proved that the calibration process clearly leads to the desired digital model of the studied area of the river.
Текст научной статьи Анализ процесса идентификации параметров морфометрии рек и водохранилищ в компьютерных моделях гидравлических расчетов (результативность и однозначность калибровки)
Компьютерной моделью гидравлических расчетов участка реки с водохранилищем называется структурированный набор цифровых данных в соответствии с используемой программой расчетов (HEC-RAS, MIKE и др.). Модель водного объекта является как бы эталонной формой заполнения гидрологических данных, что позволяет осуществлять многократные гидравлические расчеты с решением задач определенного вида, проводя замену данных в разных вариантах. Гидравлический расчет ведется по створам, нумерация створов i при подготовке данных идет от устья основного участка реки (водохранилища) против течения и отдельно от устья каждого притока, фиксируются расстояния между створами. Поперечные сечения каждого створа задаются в ориентации течения воды от условной топографической точки с высотной отметкой Z 0 - самой левой на сечении створа, каждая последующая топографическая точка сечения определяется отметкой и ее расстоянием от самой левой точки сечения. Отмечаются бровки русла, т.е. границы русла и пойм, задаются коэффициенты шероховатости nleft, n chanl, nright русла и пойм. Перечисленные данные являются базовой геометрической информацией цифровой гидравлической модели и используются во всех расчетах. Информация по гидрологии для изучаемого участка реки – это оперативные данные , предназначенные для конкретных расчетов. Таков состав данных цифровой гидравлической модели.
При расчете установившегося движения воды гидрологическая информация содержит
расходы Q i в створах и уровень воды в начале участка Z i ; гидрологическая информация при расчете неустановившегося движения содержит гидрографы притоков Q i ( t ) , граничные условия в виде хода уровней Zt ( t ) , - как правило, Z i = 1( t ) , - и начальные условия Q i (0) (неустановившийся расчет требует также задания общего периода и интервала расчета ). В результате гидравлического расчета определяются уровни во всех створах, постоянные значения Z i при установившемся движении и ход уровней Z i ( t ) на каждом створе при неустановившемся движении. Но цифровая модель участка реки является лишь идеализацией гидравлических условий, не отражая всех гидравлических тонкостей реального морфологического строения реки в принципе.
Рис. 1. Схема расчетного гидравлического у частка с нумерацией створов
Программами гидравлических расчетов не учитываются многорукавность, косоструйность, изменения шероховатости в руслах и пойме между соседними створами и многое другое. И эта идеализация принципиальна. Исправление топографии поперечных сечений и коэффициентов шероховатости проводится корректировкой параметров сечений с поверкой гидравлическими расчетами, т.е. путем калибровки базовой цифровой гидравлической модели. Принцип калибровки гидравлической модели следующий: это процесс, включающий этапы гидравлического расчета, сравнения полученных после расчета уровней с фактическими данными на постах наблюдений и оценка различий между ними, устранения этих различий путем изменения параметров сечений. Критерием калибровки является максимальное приближение полученных по расчетам уровней и объемов водохранилищ к фактическим уровням реки на створах - постах наблюдений в соответствующих гидрологических условиях и к выверенным объемам водохранилища [1,2]. Необходимость калибровки подчеркивали многие исследователи [3, 4], но ее формализация по сути началась с работ [5, 6], где даны общие принципы калибровки.
Калибровка является задачей, обратной гидравлическому расчету. Обратная задача по отношению к прямой задаче решения дифференциальных уравнений (для гидравлики это уравнения Сен-Венана и Шези [7, 8]), в принципе, некорректна по
Тихонову [9], и необходимо проводить регуляризацию задачи. Регуляризация задачи калибровки заключается во включении в ее формулировку (помимо требований максимального приближения расчетных уровней и объемов водохранилища к фактическим уровням и проектным объемам) условий обеспечения наименьшего отклонения исправленных, полученных в результате калибровки параметров описания поперечных сечений от первоначально заданных. Допустимо, однако, не включать эти условия непосредственно в формулировку задачи калибровки, а ограничиться требованием лишь малых изменений параметров модели при шагах калибровки, что равнозначно требованию небольших отклонений от начальных данных.
На профиле поперечного сечения по данным высотным отметкам земли можно проследить общее строение пойм и русла. Параметры схематизированных сечений: H – глубина русла и пойм, b –ширина потока, z – отметки дна, B -ширина реки (рис. 2).
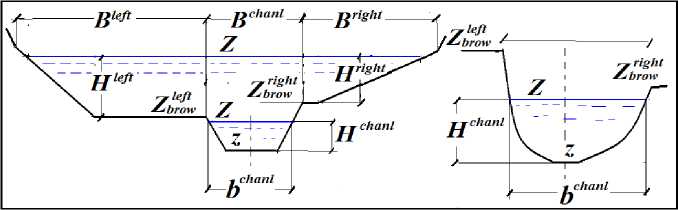
Рис. 2. Схема поперечного сечений русла и пойм, левой и правой
Итак, калибровка цифровой модели участка реки с водохранилищем для гидравлических расчетов представляет собой процесс корректировок параметров модели (ширины русла и пойм, глубины, шероховатости, расстояний). При этом на каждом шаге калибровки выбираются перспективные створы i и параметры xi их поперечных сечений, изменение которых целесообразно по сравнению с другими параметрами в смысле быстрого достижения минимума оценки близости рассчитанных и фактических уровней на створах наблюдений, как и близости к оценке объемов водохранилища, -функция F . Выбор осуществляется путем вычисления определенных оценок dF[dxi > 0 целесообразности корректировок. В этой статье процесс калибровки не рассматривается подробно, но обозначены шаги калибровки и доказывается результативность и конечность этого процесса. Кратко постановку задачи калибровки можно сформулировать следующим образом. Функция F , оценивающая близость уровней
F = У ” ( Z - Zfa c ) 2 / ^ Z, z i=H = 1 11 I
F ( Z ) = S ”„ f ( Z) ; f. ( Z) = ( z , - z^ "h A Z ,
…(1)
где AZ- определенные величины, присущие каждому створу, позволяющие привести члены указанных сумм с разницами уровней на рассматриваемых постах наблюдений к сравнимым друг с другом величинам. Здесь i – створы постов наблюдений. При этом уровни на створах связаны друг с другом функцией гидравлического расчета Н(Zx, Z^, Zn), и каждый уровень зависит от используемых параметров X (xv, x2,... xm ), в принципе от всех параметров. Под параметрами Xj, j = 1, m понимаем указанные выше ширину и глубину русла, ширину пойм, коэффициенты шероховатости, соответствующие общему строению поперечных сечений. В зависимости от размеров при большом, может быть, влиянии на уровень Z i изменения некоторого параметра на i –м створе влияние его на следующих створах уменьшается, зачастую уровень Z.+1 соседнего створа уже не испытывает сильного влияния параметра i -го створа.
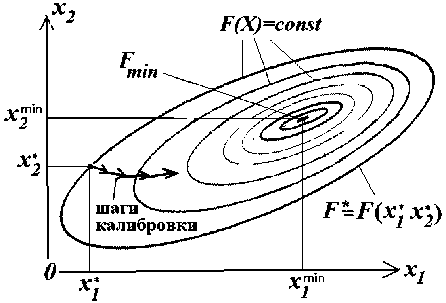
Для водохранилища, входящего в состав рассматриваемого участка реки, задаются отметка нормативных уровней: нормальный подпорный Zncorrm (нпу), уровень мертвого объема z Fv = /турасчет тгфткт \2 рагртсчет тгфткт \2 рагртсчет тгфткт у Уумо— vymo )+ У нпу — Vнпу )+ (VФПУ — VФПУ ) факт VУМО — фа кт VНПУ факт VФПУ где VypM04'T - рассчитанный объем водохранилища при уровне мертвого объема; VmO" - объем водохранилища при уровне мертвого объема фактический или принятый по проектным данным, аналогично для уровней НПУ и ФПУ. Таким образом, калибровка модели гидравлических расчетов для участка реки формализуется в виде задачи минимизации функции, которая вычисляется в результате гидравлического расчета. Осуществляются вычислительные эксперименты, состоящие из гидравлических расчетов и вычислений F - суммы квадратов относительных отклонений вычисленных уровней от фактических на створах наблюдений Fz плюс сумма относительных отклонений вычисленных объемов водохранилищ от заданных F. Выбираются параметры для корректировки модели, вносятся исправления, проводится новый гидравлический расчет. Если в задачу непосредственно включаются оценки изменения первоначально заданных исходных данных xj в связи с регуляризацией, о чем говорилось выше, и ставится требование минимума отклонений откалиброванных топографических данных от заданных первоначально по расчетным створам параметров, то оценки близости этих параметров базовой гидравлической модели от исходных можно выписать как f = ^m_Д(x5 — xj)/xj]2. Полная оценка качества калибровки базовой цифровой модели реки и водохранилища для гидравлических расчетов в этом случае запишется: F = Pz х Fz + Pv х Fv + Pf х f , где p - весовые коэффициенты, pZ + pV + pf= 1. Будем рассматривать общий случай формализации калибровки базовой гидравлической модели для неустановившегося движения воды. Формализация калибровки модели при установившемся движении та же, но без временного фактора t . В частности, можно для определенности ориентироваться на гидравлические расчеты при оперативном управлении водохранилищами, тогда t - сутки. При установившимся движении воды калибровка ведется по уровням Z в створах наблюдений, полученных в результате гидравлического расчета минимизируются разница (разбежка) рассчитанных и фактических уровней на створах наблюдений. Калибровка при неустановившимся движении минимизирует среднеквадратические разбежки Z(t) в расчетные интервалы времени или разницу максимума и минимума отклонений. Итак, X(x,x2,x3,..,xm) - калибруемые параметры: коэффициент шероховатости, ширина и глубина русла на каждом створе и др. Оперируем полным списком параметров, не разделенных по створам, поскольку изменение каждого в отдельности или группы параметров влияют на уровни пропускаемых в реке расходов в принципе на всех выше и нижележащих створах. Назовем однонаправленным такое изменение параметров поперечного сечения, что изменение каждого из них ведет к одинаковому, одному и тому же изменению уровня на створе, повышению или уменьшению уровня. По «физическим» соображениям всякое однонаправленное пропорциональное изменение параметров по некоторому векторному направлению в пространстве параметров X(xT,x2,x3,..,xm) влечет за собой монотонное направленное только верх или вниз изменение уровней Zi в принципе на всех створах i , - не только на створах, где изменялись параметры. Возможно, пропорциональность изменения параметров и изменений при этом уровней как-то связаны, но лишь «физические» соображения не дают точных соотношений между ними. Следует заметить, что качественная картина изменения уровней и других гидравлических характеристик потока при оговоренных изменениях параметров одинакова при установившимся и неустановившимся движении. Заметим также, что локальный качественный анализ изменений уровня на одном створе можно оценочно проводить по формуле Шези. Таким образом, оперируем параметрами калибровки X (будем далее обозначать просто X), уровнями Z, которые меняются монотонно при однонаправленном изменении X и оценками качества калибровки F -это строго выпуклая функция как сумма квадратов. При калибровке можно проводить разнонаправленные изменения параметров на створах, но будем рассматривать процесс как последовательные шаги однонаправленных изменений. Исследование функции F оценки калибровки гидравлической модели следует начать с обоснования квазивыпуклости функции F как функции от параметров X . Понятие квазивыпуклости функции представлено в Википедии. Возьмем определение: минимизируемая функция ква-зивыпуклая тогда и только тогда, когда для любого допустимого её значения область аргумента с меньшими значениям функции выпуклая, т.е.: F(X) квазивыпуклая, если уf* множество {X} : F(X) < F* выпукло. Выпуклая функция -квазивыпуклая; квазивыпуклая функция не обязательно выпуклая. Рассмотрим сначала функции одного переменного. Утверждение: если функция F(Z) выпуклая, а Z = Z(X) монотонная, то F(X) = F(Z(X)) -квазивыпуклая функция. Доказательство. Пусть Xp и Xg такие, что F(Xp) = F и F(Xg) = F . Возьмем точку XPQ между двумя точками ХР и Xg : Xp< Xpq< XQ. Поскольку Z = Z(X) монотонная функция от X , то Zp (Xp) < Zpg (Xpg ) < Zg (Xg), - не важно < или >. Найдутся p > 0 и q > 0, p + q = 1, такие, что Zpq (XPв) = p x ZP (Xp) + q x ZQ (XQ) Из выпуклости F(Z) имеем: F (Zpq) = F [ p x Zp (Xp) + q x Zg (Xg)] < p x F (Zp (Xp)) + q x F (Zg (Xg)) = = p x F (Xp) + q x F (Xg) = p x F * + q x F * = F * т.е. F(Xpq) = F(Z(Xpq))<F* при F(Xp) = F*, F(Xg) = F , Xp< Xpg< Xg, что и есть квазивыпуклость. ♦ Рассмотрим теперь многомерную функцию F = F (Z, Z2, Z3 ,.., Zn) от набора уровней Z = {Z,Z2,Z3,..,Zn} по створам i = 1, m, так что уровни зависят от множества параметров X = {xY, x2, x3,..,xm}, и уровень на каждом створе есть функция Z = Z (x, x2, x3,.., xm). В этом случае F= F(Z1>">Zn) = F[Z 1(X 1>X2>"xm),Z2(X1>X2,..xmV,Zn(X1>X2,"xm)]= = F (X1,X 2’A ) Анализ поведения функции F(X), исходя из свойств F = F(Z) как квадратичной функции и монотонности Zi = Zi(X) по каждому параметру Xj в отдельности показывает, что при бесконечном увеличении каждого параметра F стремится к определенному конечному значению, большему Fmin , поэтому ближе к Fin, начиная от некоторых значений параметров Xj F(X) приобретает форму замкнутой фигуры (рис. 3). Для справедливости утверждения о квазивыпуклости функции F(x1,x2,..Xm) аналогично одномерному случаю недостаточно условие простой монотонности функций Zi = Zi(X1,X2’..’Xm), i = 1, m независимо друг от друга. Введем понятие согласованной монотонности. При согласованной монотонности при линейном однонаправленном изменении параметров Х{x1,X2,X3,..,Xm} от X к X1', в общем случае однонаправленного на нескольких створах, функции Zi(X), i = 1,n меняются подобным образом: Z(X) = Z(X') + r x R(X), i = 1, n; r. = const ; R(X) - монотонная, R(X) = 0. Рис. 3. Форма функции F(X) вблизи минимума Утверждение: При согласованной монотонности для любых вариантов параметров X7и X7' с соответствующими им наборами функций Z; и Z", набору параметров X7":X7< X7" < Xs (т.е. х' < х"'< х", j = 1, m) соответствует Z": Z < Z" < Z, и найдутся p>0, q>0, p+q=1, такие, что Z (Xт) = p x Z (X') + q x Z (X") единствен ные для всех i = 1, n. Доказательство. Если найдутся две функ ции Zp (X'), Zn (Xw), их можно представить как Z,(X") = p, xZn(X') + q^ xZn(X-'), Z^{X") = p, xZ,(X)+q, xZ,(X), p^,q, > 0, pn + q, =1; p,,q, > 0, p, + q, =1, то при со- гласованной монотонности Z^ (X") = Z, (X) + r, x R(X^, также как Z ,Х'') = Z ,X ) + r, X R(X), Zn (Г) = Z, (X) + r, X R (X), Z,(X”) = Z,(X") + r, x R(X"'). Тогда для первой функ- ции r,R (X”') = p, X r,R (X')+q, X r,R (X') R (X”^ = p, x R (X)+q, x R (X ’), или также R(X'") = p x R(X)+q x R(X") для второй функции, -одно и то же уравнение с разными р и q. Но по условиям к этим коэффициентам (в начале доказательства), необходимо p, = p, = p, q, = q, = q .♦ Заметим, если наоборот, определить согласованную монотонность, как одно для i = 1, n, условие Z (Т) = p х Z (X) + q x Z (X) , i i i , доказывается подобие изменения Zi(X) на всех створах. Согласованная монотонность интуитивно представляется из «физических» соображений: при однонаправленном изменении некоторых параметров меняются уровни потока, но выдерживается определенный порядок этих изменений. Невозможно, чтобы в условиях спокойного потока в одном створе уровень повышался, потом понижался. Превалирующее большинство рек имеют спокойное течение и в половодье. При бурном и только бурном потоке горной реки картина аналогична. Более сложно, если спокойный и бурный потоки перемежаются как на предгорных реках с порогами. Переходим к основному Утверждению: Если F(Z 1,Z2..,Zn) = ^n f.(Zi), все f - выпуклые, а Z = Zi(xp x2,..,Xm), i = 1, n , - согласованно моно- тонные функции, то при однонаправленном изме- нении параметров F(xl,-, xm ) = F [Z( X1,•., xm )v> Zn (X1,•., xm )] - ква- зивыпуклая функция. Доказательство. Пусть Xp (xp, xp, xp,.., xm ) XQ(xQ,xQ,xQ,..,xQ) такие, что F(Xp) = F* и и F ( Xq ) = F *. При F (Xp) = £/ (Xp) =Е/ * =F *, F(Xq) = E ifq(Xq) = 1 if* =F*. Возьмем между двумя точками X p и Xp < Xpq < Xq .(по одним параметрам x этом также XPQ XQ: может быть xp < xPQ < xQ по другим параметрам xp > xPQ > xQ, указанный знак < условен, важно, что изменение параметров однонаправленное, т.е. изменение каждого параметра влияют на уровни одинаково). Поскольку каждая Z = Z (X) = Zi (x, x- ,•• xm) монотонная функция по каждому из xi, то по однонаправленной совокупности {xi,x2.;xm} Zp(Xp) < ZpQ(XpQ) < Zq(Xq), -или Zp(Xp) > Zpq(Xpe) > Zq(Xq) , не имеет значения, что рассматривать. Поскольку кроме того все функции Zi = Zi (X) согласованно монотонные, найдутся p, q, p + q = 1, такие, что для всех Vi = 1, n функций можно записать Z!4 (Xpq ) = p XZip(Xp ) +q XZq(Xq ) . Из выпуклости ft (Z) имеем тогда для всех i: /i (Zipq) = /i [ p x Zp (Xp) + q x Zq (XQ)] < p x / (Zp) + q x f (Zq) = =p Xf( xp )+q Xf( xq )=p Xfp *+q X fq * Тогда f ( x„ )=Е/i (Z”) < p x^f (Z)+q x Zf^ (Zq)= =p xEf''+q xEf' *=p x F *+q x F *=F * Т.е. F (Xpq) = F (Z (Xpq)) < F при F (Xp) = F, F (XQ ) = F , Xp < XpQ< Xq , - это квазивыпуклость. Таким образом, когда «текущие» перед следующим шагом процесса калибровки параметры X*{x*, x*, x*,..x*} делят все пространство параметров на октанты и в октанте, который соответ- ствует нужному однонаправленному изменению параметров, оценочная функция F(X) квазивы-пуклая, при этом F = F(X ). Нужное изменение параметров определяется необходимостью под- нять или опустить уровни Z = Z (x, x2,.., xm), i = 1, n , приближая их к фактическим уровням, заданным на постах наблюдений, а также увеличить или уменьшить расчетные значения характерных объемов водохранилища с целью приблизить их к фактическим (проектным) объемам. Может рассматриваться один створ или некоторая совокупность створов, на которых необходимо поднять или опустить уровни, поэтому многомерная геометрическая картина проявления квазивыпуклости функции F(X) в пространстве параметров может быть различной на разных шагах калибровки. Квазивыпуклость может проявляться в октанте в пространстве всех m параметров, и на многомерной плоскости (затрагиваются m-1 параметр), и на многомерном ребре с m-2 параметрами. Элемент многомерной геометрии, в пределах которого проявляется квазивыпуклость F(X), зависит от числа параметров однонаправленного изменения, выбранных для уменьшения оценки F(X). Квазивыпуклая функция унимодальная, имеет единственный минимум. Рис. 4, на котором схематично даны изолинии равных значений F(X) на множестве координат X(xt, x2), иллюстрирует шаги процесса калибровки гидравлической модели. Выпуклое множество X:F(X) < F* (рис. 4) ограничено, характеризуется диаметром d и точка X*{x.",x1‘,x1Vx**} «текущих» параметров процесса калибровки по самой процедуре построения находится на границе множества. Шаг калибровки заключается в корректировке параметров на определенные величины Az, AB, AH, An изменения высотных отметок, ширины и глубины русла и пойм, которые могут выражаться абсолютными значениями, при этом точность достижения решения при калибровке полагается на практике ДБ=3-10 м, Дz, ДН=7-15 см. Изменение шероховатости Дn принимается не менее 0,0025. Рис. 4. Изолинии равного значения F(X) и схема действий по калибровке модели Шаг калибровки перемещает текущую точку параметров X*{xx*, xx*, xxV.x.*} внутрь выпуклого множества X: F(X) < F*, на следующем шаге диаметр множества меньше предыдущего и так происходит до тех пор, пока с заданной точностью корректировок параметров мы не достигнем точки минимума. Процесс калибровки конечен, поскольку заданы конечные размеры изменений параметров. Задача калибровки, таким образом, представляет собой поиск точки минимума в координатах калибровочных переменных Fin(Xm”); при этом совсем не обязательно этот минимум окажется равен нулю F^ (X™ ) = 0, - общий случай Fiп(X™ ) > 0. Если F^n (X) =0, достигается полная калибровка гидравлической модели, F^n(X) >0 указывает на необходимость добавления новых расчетных створов на участке или/и добавления гидрологической информации. Рассмотрим такой вопрос: в какой степени меняется свойство квазивыпуклости при отсутствии равномерной монотонности Z = Z(X) = Z(x,x2,..xm), поскольку свойство равномерной монотонности основано на «физических» соображениях, что в природе может выполняться не абсолютно, а с определенной ограниченной неточностью. Повторяем, пусть Xpx xp, xp, xp,.., xp ) и XQ(xQ,xQ,x3Q,..,xQ) такие, что F(Xp) = F* и F (Xq ) = F *. При этом F(Хр) = 2 f (Xp) = 2 J’* =F *, также F(x,) = 2 Ji(XQ) = 2 Ji * =F *. Возьмем Xpq между двумя точками Xp и Xq : Xp < Xpq < Xq .(по одним параметрам x может быть xp < xPQ < xQ по другим параметрам p PQ Q x > x > x ). Поскольку каждая Z. = Z_(X) = Z (x, x2,..xm) монотонная функция по каждому из однонаправленно корректируемому xj, то по совокупности однонаправленно изменяемых {x15x2.., xm } имеем Zp (Xp) < Zq (XpQ) < Zq ( Xq ), или Zp(Xp) > Zpй{XpQ) >Zq(Xq), не имеет значения. Поскольку каждая функция Z, = Z, (X) монотонная, найдутся Pt, qi, pi + q,= 1, так, что для каждой из них можно записать Zp (Xpq) = p, х Zp (Xp) + qt X Z, (Xq) и из выпуклости Ji(Z) имеем для каждого i: f (ZP) = f [P, x Z? (Xp) + q, х Zq (Xq )] < p, x f (Zp ) + q, х f (Z,) = = P,x f( Xp) + q,x fiXq ) = p, x fi * + q, х fq * Тогда F(Xpq) = 2f(zF) < X[p, X f.(z') + q, X f,(zq)]= 2[p, X f'* + q, X fq*]= z zz = 2[(p+a) x/7 *+ (q+n)X f 7 * ]= = p xX fp *+ qх 2 fq * +2 [pxp *+n,f? * ]=(p + q)х F * + 2 [pxp *+n,f? *] z z zz = F * +X[p,fp * + nJ? * ] Здесь: n nnn p=~2p,, q=~2q,, p,= p,-p, n=q,-q, Xp, = 0, Xn =0 n ,=i n ,=i ,=i из p + q = 1, p, + q,= 1 V,, p,+ n, = 0 V,, p,\< j^, J<^^. Тогда: nn F(Xp,) < F" + 2p,x(f" - f?■); A = Xp, X U'• -f'•); =1 i=1 Итак, F (Xp)< F * + A < F *, если A < 0. Т.е. F (Xpq) = F (Z (Xpq)) < F при F (Xp) = F, F(XQ) = F , A < 0, - квазивыпуклость соблюдается. При A > 0 необходим дополнительный анализ. Заметим сначала, что Д - небольшое число в сравнении с F , так как содержит одни разности близких величин, а множители р, ограничены: |р, \ < у2 , и кроме того nn 2р,= 0; 2(fip* - fq*) = 0; i=1 i=1 При A > 0 имеем F(Xpq) < F + A, возможны два случая: F(Xp) < F* < F* + А и F * < F(Xp) < F* + A. Пер- вый случай означает, что выпуклое множество {X}: F(X) < F* существует, и это соответствует квазивыпуклости F(X). Во втором случае множе ства {X}: F(X) < F* нет, что может означать невозможность достичь результата калибровки, соответствующего заданной точности поиска, приведенной ранее: ΔВ=3-10 м, Δz, ΔH=7-15 см, Δn =0,0025. При такой ситуации необходимо рассмотреть большее число створов с дополнительными данными по гидрологии. Выводы: практические расчеты по калибровке гидравлических моделей показывают, что приведенные выше ситуации имеют место, поскольку зачастую пользователь для облегчения калибровки экономит на числе створов и объеме гидрологических данных.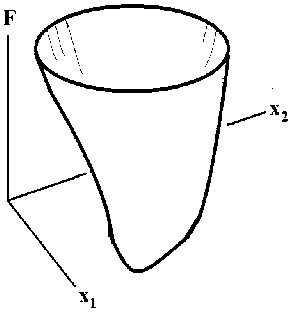
Список литературы Анализ процесса идентификации параметров морфометрии рек и водохранилищ в компьютерных моделях гидравлических расчетов (результативность и однозначность калибровки)
- Никифоров, Д.А. Калибровка гидравлических моделей рек и водохранилищ. Влияние корректировки параметров программной модели на точность гидравлических расчетов//Современные проблемы водохранилищ и их водосборов. Труды междунар. научно-практ. конф. Управление водными ресурсами. Гидро-и геодинамические процессы. Том I. -Пермь, 2013. С. 253-260.
- Никифоров, Д.А. Влияние корректировки параметров программного комплекса HEC-RAS на точность гидравлических расчетов и формализация процесса калибровки гидравлических моделей рек и водохранилищ//Чистая вода России. Сб. материалов XII междун. научно-практ. симпозиума. -Екатеринбург, 2013. С.226-234.
- Грушевский, М.С. Неустановившееся движение воды в реках и каналах. -Л.: Гидрометеоиздат,1982. 288 с.
- Кюнж, Ж.А. Численные методы в задачах речной гидравлики: практ. применение/Ж.А. Кюнж, Ф.М. Холли, А. Вервей. -М.: Энергоиздат, 1984. 255 с.
- Корень, В.И. Определение геометрических и гидравлических характеристик речного русла путем решения обратных задач для уравнений Сен-Венана/В.И. Корень, Л.С. Кучмент//Водные ресурсы. 1973. №4.С. 83-100.
- Левит-Гуревич, Л.К. Математические основы калибровки компьютерных гидравлических моделей рек и водохранилищ/Л.К. Левит-Гуревич, Д.А. Никифоров//Чистая вода России. Сб. материалов XII междунар. научно-практ. симпозиума. -Екатеринбург, 2013. С. 190-198.
- Агроскин, И.И. Гидравлика. 4-ое изд./И.И. Агроскин, Г.Т. Дмитриев, Ф.И. Пикалов. -М.: Энергия, 964. 352 с.
- Штеренлихт, Д.В. Гидравлика. Учебник для ВУЗов. 3-е изд. -М.: КолосС, 2004. 656 с.
- Тихонов, А.Н. Методы решения некорректных задач. 2-ое изд./А.Н. Тихонов, В.Я. Арсенин. -М.: Наука, Главная редакция физико-математической литературы, 1979. 564 с.


