Анализ процесса обучения как сложной системы

В последнее время большое внимание, ктическом исследованиях уделяется вопросам изучения функционирования сложных систем, то есть таких систем, которые характеризуются большим числом элементов и богатством внутренних связей. Рассмотрим один из этапов моделирования сложной системы на примере процесса обучения студентов технических специальностей.

Как известно, обучение представляет собой процесс взаимосвязанной деятельности «преподавателей» (преподавание) и обучающихся (учени е) в педагогической системе. При анализе эффективности работы этой системы необходимо уметь грамотно выделять подсистемы и базовые элементы. Уровень детализации зависит от цели, которая является основой исследования. Процесс постройки иерархического разбиения исследуемой системы не может быть формализован и "золотая середина" числа уровней иерархий полностью определяется опытом, интуицией и способностью неформального мышления исследователей. Проиллюстрируем это на примере.

Пусть необходимо построить математическую модель процесса обучения молодежи . В этом случае в качестве элементарных систем можно взять школу, высшее или среднее учебные заведения. Если такого же типа задача будет решаться, например, только для Университета, то в качестве элементарных систем здесь удобно выбирать факультеты, далее - учебные группы. Этот выбор зависит от того, какие цели преследует исследователь при построении модели обучения. Определяя эффективность работы Университета по подготовке специалистов, рассматриваем в качестве элементарных систем группы, обучающиеся по интересующей как при теоретическом так и при пра специальности.

Свойства всей сложной системы зависят не только от свойств составляющих, но и от взаимодействия последних между собой (две системы, состоящие из одинаковых элементов, но с различной структурой взаимодействия, считаются различными).

Характеристики состояния описывают наиболее важные факторы, определяющие процесс функционирования системы, процесс изменения ее внутренней сущности.

Система представляет собой:

• 1)    сов окупность элементов (счетное множество),

• 2)    качества системы в целом присущи только ей и не присущи никакому ее элементу,

• 3)    элементы системы характеризуются состояниями, совокупность которых образует состояние системы в целом (характеристики состояния описывают наиболее существенные факторы, характеризующие процесс),

• 4)    с течением времени каждый элемент может переходить из одного состояния в другое, тем самым процесс функционирования системы в целом моделируется изменением состояний ее элементов.

Пусть ω ( t ) – характеристика состояния некоторой системы и Ω – множество всех возможных ее состояний, то есть ω ( t ) ∈ Ω для всех t ∈ (0, T ) , где (0, T ) – интервал времени функционирования системы.

Пусть элементы системы пронумерованы числами 1,2,...,m (если их число бесконечно, то m = ∞ ). Обозначим через si(t) характеристику состояния i-го элемента, которая прини- мает значения из конечного множества Si, где si(t) е Si. Без умаления общности можно считать, что si (t) - скалярная величина.

Тогда вектор

® ( t ) = ( s 1 ⁽ t Ь s 2 ⁽ t ),..., s m ⁽ t )) ^е П -1 3 = ^S ,..., определяет характеристику состояния системы.

Общее число возможных состояний системы (обозначим это число k . ), равное числу значений, которые может принимать характе-

m ристика состояния го(t), равно kш = П ki , где i=1

k i - число возможных состояний каждого элемента. Далее считаем, что число элементов в системе бесконечно ( m = да ). Это означает, что характеристика состояния o ( t ) представляет собой вектор бесконечной размерности, и тогда число состояний системы равно бесконечности. При построении модели каждому состоянию соответствует некоторое уравнение, определяющее его изменение. Системы с бесконечным числом уравнений не слишком удобны для использования.

Пусть множество элементов системы будет разбито на попарно не пересекающиеся подмножества 1: m = E 1 + E ₂ + ... + E _v , такие, что E i n E j = 0 при i * j ; i , j е 1: v и что множество состояний S ( E i ) для всех элементов данного подмножества одно и то же. Эти подмножества назовем группами. Таким образом, элементы системы разбиваются на ряд групп. Из конкретной интерпретации элементов следует, что элементы относятся к разным группам в том случае, если множества S i их возможных состояний существенно различны, что следует из конкретной интерпретации элементов.

Число групп конечно. Это связано с множеством состояний, ибо если число групп бесконечно, то в этом случае вектор характеристик, описывающих состояние системы в целом, будет иметь бесконечное число компонент, а это в некоторых случаях может вызвать значительные трудности при моделировании.

Пусть m j ( t ) - число элементов i -ой группы, находящихся в состоянии s i j е S i , то-

состояние группы E i однозначно можно определить так называемым «урезанным» вектором ( m i 1 , m i ₂,..., m_ik , ) для описания состояния группы, в котором число элементов, находящихся в одном состоянии, выражается через остальные m_ij .

После того как описан вектор состояний групп, состояние системы в целом можно описать не вектором щ ( t ) , а вектором

M ( t ) =< M , ( t ), M 2 ( t ),..., M m ( t ) >  или матрицей

	m 11	m 12	•   m 1 k 1
M =	. .	. .	. ..

.    ^m v 1

Таким

{ m ij | i е 1: m ;

^m v 2

m v k v массив

чисел

ki гда mi (t) = ^ mj (t) - число элементов группы

j = 1

E i , где k i = | S i | - число возможных состояний, в которых может пребывать каждый элемент i -ой группы. Тогда состояние i -ой группы опре-

деляется вектором

M i ⁽ t ) =< ^m i 1 ⁽ t X ^m i 2 ⁽ t Х-, m^ ⁽ t ) > .

Рассмотрим вектор состояний группы E i . Предположим сначала, что I — я группа

содержит конечное число элементов m i , при

чем m i известно изначально и не меняется в процессе функционирования системы. Тогда

образом, j е 1: k i } полностью описывает

состояние системы в целом. Здесь существен

но, что сами элементы, их состояния и соответственно разбиение на группы выбираются таким образом, чтобы состояние всей системы в целом, с одной стороны, полностью определялось состоянием элементов, а с другой - определяло бы эффективность функционирования системы (соответствовало целям построения модели).

Оценим число возможных состояний системы. Для каждой группы число элементов

m j может принимать значения от 0 до m i , а

вектор состояния группы имеет k i место, тогда общее число возможных состояний группы равно

mi mi + ki -1 .

В связи с этим общее число состояний системы можно вычислить по формуле

что

V

П C

i = 1

mi mi+ki -i

значительно

меньше,

чем

k .    (

V km > FTCm', , ). Такое описание состояний го            mi + ki -1

i = 1

позволяет в свою очередь сократить число математических выражений, описывающих систему.

Произведем подсчет числа состояний при v = 2, k 1 = 2, k ₂ = 3, m 1 = 5 и m ₂ = 3

(рассмотрим «урезанный» вектор для описания состояния группы). В этом случае число состояний равно C ₅ ⁵ _+2-1 • C ₃ ³ _+3-1 = 6 - 10 = 60 . Даже в таком простом случае число состояний достаточно велико.

Для иллюстрации расчета числа состояний рассмотрим следующий пример.

Пример. Для разработки стратегии обучения студентов на спецкурсах нас интересуют побудительные к изучению мотивы. Пусть в

каждый момент времени студент изучает какой-то курс по специальности, то есть состояние студента в данном исследовании зависит от времени. В качестве объекта исследования выбирается студенческая учебная группа, состоящая из m человек. Будем считать, что такими мотивами являются:

• 1)    изучаю, потому что необходимо,

• 2)    изучаю, потому что интересно,

• 3)    изучаю, потому что нахожусь вместе с друзьями.

На самом деле побудительных мотивов может быть столько, сколько человек в группе, а может даже еще больше, но для описания состояний и подсчета их числа ограничимся только этими тремя мотивами. Элементами системы считаем студентов рассматриваемой группы. В каждый момент времени t (что соответствует изучению какого-то определенного спецкурса) состояние i- го элемента принимает одно из трех значений (в зависимости от спецкурса). Тогда студент, опрашиваемый i -м, имеет следующее множество состояний:

S i (t ) = ( ” необходимо”,”интереснО',”с д р узьями” ) .

В этом случае общее число возможных состояний системы, равное числу значений, которые может принимать характеристика состояния < я ( t ), равно к _т = 3 ^m .

Так как к = 3m может быть в зависи-ω мости от m очень большим числом, то состояние системы можно описывать не вектором ®( t) = ( 51 (t), 5 2( t),..., sm(t) >еЦ   „Si = S,

,..., а вектором

M(t) = (mнеоб. (tX mинт.(tX mдр.(t^ , где m необ. ( tX m инт.( tX m др.( t) - число студентов, находящихся в состояниях «необходимо», «интересно», «с друзьями» соответственно, причем mнеоб. (t) + mинт.(t) + mдр. (t) = m и

• ⁰ ^ m необ. ⁽ t X m инт. ⁽ t X m др. ⁽ t ) ^ m .

Отсюда следует, что в этом случае количество значений, которое может принимать характеристика M(t) , то есть число состояний, равно C m + _3-1 , а это при достаточно больших m значительно меньше, чем к _т .

В рассмотренном примере для всех элементов множество возможных состояний одно и то же: S i ( t ) = S j ( t ) для всех i , j e 1: m .

Процесс функционирования системы проявляется в последовательной смене состояний из множества M с течением времени, то есть моделируется переходом системы из одного состояния в другое. Такая смена состояний математически описывается изменением их характеристик, для описания которых используются дифференциальные или разностные уравнения в той или иной форме.

Давая различные интерпретации характеристикам состояний, можно получать соответствующие целям исследования модели. Таким образом, характеристики состояний систе мы, а в свою очередь характеристики состояний элементов - это множества, элементы которых зависят от вложенного в них смысла. В качестве характеристики состояния mi(t) могут быть, в зависимости от конкретного исследования, выбраны различные величины. Например, это может быть Pm (t) - вероятность того, что в данный момент времени t ровно mi элементов находятся в состоянии Si, или математическое ожидание mi (t) числа элементов, находящихся в состоянии Si в момент времени t, или дисперсия Dm (t), и т.п.

Процесс перехода элементов из одного состояния в другое можно изобразить в виде графа, у которого вершинам сопоставлены состояния элементов, обозначенные соответ-ствующимихарактеристиками x i , а дуга ( i , j ), направленная от вершины x i к вершине x j , характеризует интенсивность X i. перехода элементов из состояния s i в состояние s j (эта дуга в графе существует только тогда, когда существует возможность перехода из состояния s i в состояние s j ). Физический смысл интенсивности X ij зависит от конкретного содержания характеристик состояния m i ( t ) и времени, за которое рассматривается переход.

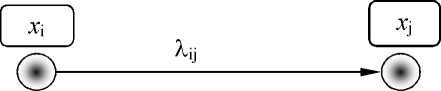
Рисунок 1. Граф перехода элементов

Таким образом, при описании модели функционирования системы приходим к графу G(VE) :

• 1)    V - множество вершин графа (элементы - характеристики вершин графа);

• 2)    E - множество дуг, которое соответствует множеству событий (каждое событие характеризует переход из одного состояния в другое);

• 3)    каждый маршрут на графе от начального состояния до конечного состояния - одна из возможных реализаций функционирования системы (начальное и конечное состояния выбираются исходя из целей исследования).

Пример. Пусть имеется m порций учебной информации. Нас интересует оптимальная стратегия обучения, то есть выработка рекомендаций по организации последовательности поступления порций информации, которая даст наибольший эффект обучения. Изобразим при помощи графа структуру учебной информации. Вершинам сопоставим учебные элементы, а ребрам - связи между этими элементами, которые являются существенными с точки зрения преподавателя. Но так как каждый преподаватель при изложении учебного материала по своему структурирует учебную информацию, а кроме того в различные перио- ды времени или с разными группами студентов опять же меняет структуру изложения, то один и тот же учебный материал может структурироваться по-разному. А это означает, что граф, соответствующей данной учебной информации может принимать различные формы.

Рассмотрим три подсистемы (структуры) подачи учебной информации, являющиеся частью общей системы организации последовательности поступления порций информации, а именно

• •    индуктивный метод, который означает переход от знаний меньшей общности (X i ) к знаниям большей общности (Z), изложение ведется от частного к общему, от элементов к це-

• Рисунок 2. Индуктивный метод

• •    дедуктивный метод – это переход от изучения более общих положений и теорий (Z) к частным знаниям (X i ) (применяется, как правило, в теоретических науках, базирующихся на математических методах) (рис.3);

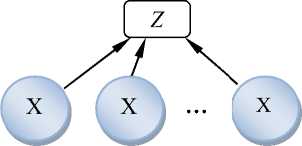
Рисунок 3. Дедуктивный метод

• •    линейная структура, которая представляет собой взаимно-однозначное отображение элементов знания одинаковой общности, каждый предыдущий учебный элемент связан только с одним последующим (рис.4.).

Рисунок 4. Линейная структура

Индуктивные и дедуктивные методы обучения раскрывают логику организации и осуществления учебно-познавательной деятельности. При использовании этих методов обучения источником получения знаний являются:

• а)    словесные методы (источником знания является устное или печатное слово);

• б)    наглядные методы (источником знаний являются наблюдаемые предметы, явления, наглядные пособия);

• в)    практические методы (учащиеся получают знания и вырабатывают умения, выполняя практические действия.

Но при применении всех методов содержание учебного материала раскрывается определенным логическим образом - индуктивно или дедуктивно.

Изображение графа является достаточно компактным и информативным способом представления структуры системы и значительно облегчает ее анализ, позволяет «показать» состав и подчинённость функциональных элементов системы, направленных на достижение поставленной цели.

Перечислим ряд типичных задач, решаемых теорией графов:

• 1.    Формализация и построение общей структурной модели объекта на разных уровнях его сложности.

• 2.    Анализ полученной модели, выделение в ней структурных единиц (подсистем).

• 3.    Изучение уровней структуры иерархических систем: количество уровней, количество межуровневых и внутри уровневых связей.

• 4.    Анализ эффективности функционирования данной системы, поиск оптимальной структуры, определение ее устойчивости.

Описанные выше приемы позволяют использовать элементы теории графов для одновременного решения нескольких важных задач образования. В педагогике с помощью графов можно оценивать полноту и логичность учебного курса, изучать межпредметные связи, анализировать содержание учебных единиц, оптимизировать структуру изложения учебного материала, оптимизировать, исходя из цели, процесс обучения и так далее.