Анализ процесса развертывания окололунной тросовой системы с учетом притяжения Земли

Актуальность исследований динамики и разработка законов управления движением тросовых спутниковых группировок объясняется возможностью создания космических систем, состоящих из нескольких малых космических аппаратов, соединенных тросами. При этом входящие в группировку аппараты совершают согласованный полет. Такая система обладает легкостью и большим разнообразием конфигураций, и может применяться в задачах исследования космического пространства, планет и т. п. Обзор применения космических тросовых систем приведен в работах [1; 2].

Многие проекты освоения Луны и Марса предполагают использование космической стан-

Исследование выполнено при финансовой поддержке РФФИ и Государственного фонда естественных наук Китая в рамках научного проекта № 21-51-53002.

ции на окололунной орбите [3–6]. Она может служить космическим портом на орбите Луны, который сможет обеспечить жизнеобеспечение длительных экспедиций на поверхности Луны, а также станет отправной точкой для исследования глубокого космоса.

В работе рассматривается развертывание радиальной космической тросовой системы, состоящей из космической станции и малого космического аппарата, на окололунной орбите с учетом притяжения Земли (рис. 1).

Развертывание производится по закону управления, который обеспечивает развертывание троса на заданную длину при небольших отклонениях от вертикального положения. Приводится сравнение процесса развертывания при наличии притяжения Земли и без его учета.

1.    Математическая модель

Рассматриваемая в работе механическая система представлена на рис. 2. Она состоит из кос-

1оСМ1ЛЧЕск|ЛЕ АППАРАТЫ И технологии двиган

Том 5

мической станции D и малого космического аппарата B , который прикреплен к станции невесомым нерастяжимым тросом длины l_b . Станцию будем считать цилиндром, масса которого m_d , длина d , радиус ρ _d . Спутник рассмотрим как шар, масса которого m_b , радиус ρ _b . На рис. 2 v – угол истинной аномалии станции; θ – угол истинной аномалии Луны; β – угол отклонения центральной оси спутника В от локальной вертикали; φ – угол отклонения троса, соединяющего станцию и спутник, от оси симметрии спутника; δ – угол отклонения оси симметрии станции от троса в месте его кре-

пления к станции; r_b – радиус орбиты спутника B . Станция движется по окололунной возмущенной орбите радиуса r_d .

С помощью второго закона Ньютона и теоремы об изменении кинетического момента запишем уравнения движения [7]:

т ь Г, = - T + G m + G b , m d Y d = - T + G m + G d ,

Jb to, = to, x J, to, - r, x T - M mm - M ^,        (1)

Jd to d = to d x Jd to d - rd x T - M m - M d, где    Gm =-mbцmrb |rb |-3,      Ge = -mbцerb |rb |"3,

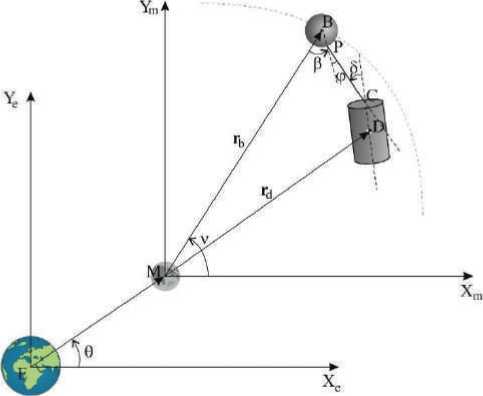
Рис. 1. Радиальная окололунная тросовая система

^G m = — m d M Mdd ¹ r d ¹ - ³ , ^G d = — m d H E r d ¹ r d ^{1 - 3 —} векторы сил притяжения Луны (с индексом m ) и Земли (c индексом e ), действующие на спутник B и станцию D , соответственно; T = { T sin(P + ф), -T cos(p + ф), 0 } , T = - T - векторы силы натяжения троса, €0 _b = { 0,0, v + p } T , CD d = { 0,0, v + Р + Ф + 8 } - угловые скорости спутника B и станции D относительно центра масс механической системы; матрицы моментов инерции спутника B и станции D :

b

( J bx

I 0

J_by 0

0  ,  Jd =  0

Jbz J        I 0

0    0 ^

J_dy 0

dz J

Радиус-векторы, задающие положение станции и спутника в орбитальной системе координат:

r _d

cos vI pb sin P + lb (P + Ф) + - sin(p + Ф + 5) I- sin v I Гь - pb cos P - lb cos(p + Ф) - - cos(p + Ф + 5

V                            ²                   /         X                                     ²                 .

sin v | p^ sin P + lb (P + ф) + — sin(P + ф + 5) | + cos v I rb - p6 cos P - lb cos(P + ф) - — cos(P + ф + 5

r6 ={rb cos v, rb sin v,0}r.

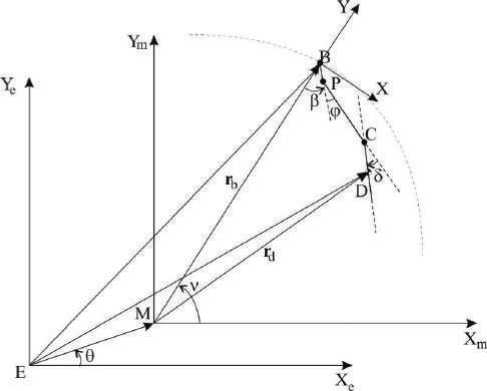
Рис. 2. Механическая система

Гравитационные моменты, действующие на спутник B и станцию D , обусловленные притяжением Луны, в общем виде записываются как [8]:

'3цM (Jbz - Jby)MByMBz 3ЦM (Jbx - Jbz)MBzMBx 3ЦM (Jby m m =I

I               k b Г              ’               k b Г              ’

- J bx ) MB z MB y '

I r b Г                  ,

_Mm _ J 3 Ц M ( ^Jdz - ^Jdy ) ^MD y ^MD z 3 ц M ( J .

^M d = I               I 13                ’

Jdz) MDzMDx 3цM ( Jdy - Jdx) MDzMDy ' II3                ,                   13 1 rdl                                        kdl                    J где векторы MB = r , MD = r (рис. 2).

Положение Луны относительно Земли задается вектором:

^P M cos ⁶  , ^P M sin ⁶  ,0 I ,

1 + e_M cos 6 1 + e_M cos 6

где e , ρ – эксцентриситет и фокальный параметр орбиты Луны. Движение Луны вокруг Земли описывается уравнением [9]:

°=_A ^E" ( 1 + e M cos ⁶ ) 2^, V ^p m

где µ – гравитационный параметр Земли.

Запишем в общем виде выражения гравитационного момента, действующего на спутник B и станцию D и обусловленного притяжением Земли:

m b =<

'3 ц E ( Jbz - J by ) EB y EB z 3 ц E ( J bx - Jte) EB z EB x 3 ц e ( Jby - J b X ) EB z EB y' 1                 k b l3                ’                k b l3                ’                 k b Г                1

3 ц E ( J* — J dy ) ED y ED _z 3 ц E ( J_dx - J dz ) ED z ED _x 3 ц e ( J dy - Jd x ) ED z ED y

I rd Г             ’            kd Г             ’            kd Г где векторы EB = EM + rb, ED = EM + rd.

Из первого уравнения системы (1) выразим силу натяжения троса:

^T = 8 m -  - 7 I ^{( 1 +} e M cos ⁶ ) | ^{V r}b ^{+ 1 V r}b l (( - 4 e M r P M sin ^(v - ^{26 ) - 8} r b P M sin ^(v - ^{26 ) +}

+ 2 e ² r ² cos 26 + 8 e..r² cos 6 - 4 er p  sin v + ( 2 e² + 4) r ² + 4p² )/(1 + e_M cos 6 ) ² )² +

Mb          Mb         Mb M         M     b    MM

+ ц _E p _M ( cos v cos 6 + sin v sin 6 )]/

( -4 er pM sin (v - 26 )-8 r p^ sin (v - 6 ) + 2 e 2, r2 cos26 + 8 erK2 cos 6 - 4 er ры sinv + (2 e2 + 4) r2 + 4p2 ^2 Mb M              b M             Mb          Mb         Mb M         M     bM

<                                                (1 + eM cos 6 )2

u_b = ( l ^b max l ^b ) Г 1 v - ( р + _ф + 5 ) J b _) .                                (3)

b max     V                     bb max /

Выражая из (3) l_b и дифференцируя по t , получим:

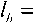
V

7 Л •

v

L 2

¹ b max V

Р + Ф l b l b max

). ( lb max - lb ) f v    ( P + ф ) lb   ( Р + Ф ) ^^

. lb ² lb lb b max                b max          b max

⁽ l b max - l b ) l b f ^{v   (в + ф)} l b

2-Ч lb max       2      lb max

Таким образом, в систему уравнений движения космической тросовой системы входят уравне- ния (1) без первого уравнения, уравнение (2) и уравнение (4).

1оСМ1ЛЧЕск|ЛЕ АППАРАТЫ И ТЕХНОЛОГИИ ЕКЙЙЙМЕЯ

Том 5

2.    Численные результаты

При численном моделировании использовались следующие массово-геометрические параметры тросовой системы: масса станции md = 2000 кг, ее длина d = 2 м, радиус ρd = 1 м, масса спутника mb = 20 кг, его радиус рb = 1 м, конечное значение длины троса lbmax=500 м, максимальная скорость развер- тывания Vmax = 1 м/с. Начальные условия: 0О=п/2 рад, vо = -п/2 рад, в = 0,01 рад, 5о = Фо = 0 рад, lbо = 0,01 м, v = 0,00066 рад/с, rb0 = 500 км, в0 = 50 = р>0 = 0 рад/с, lb0= 0,00033 м/с.

На рис. 3–6 показаны графики изменения параметров системы при ее движении по возмущенной (сплошная линия) и невозмущенной (штриховая линия) окололунной орбите.

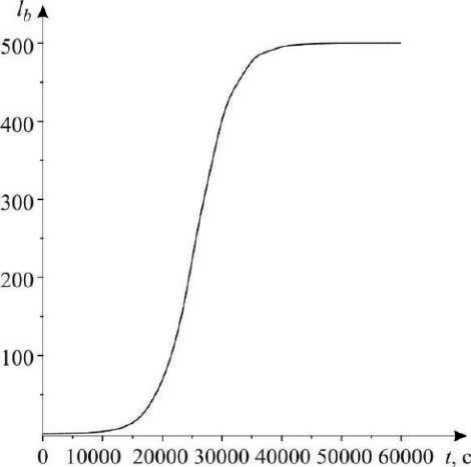
Рис. 3. Изменение длины троса b_b ( t ) и скорости изменения длины троса l_b ( t ) при развертывании космической тросовой системы

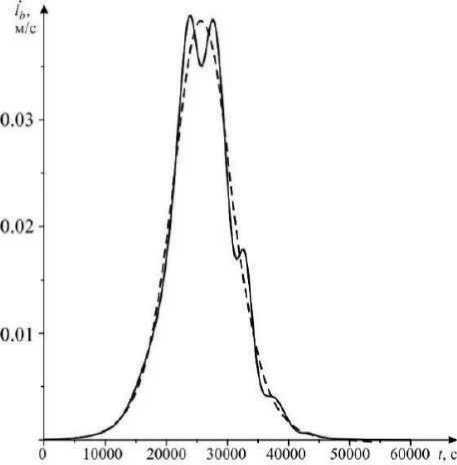
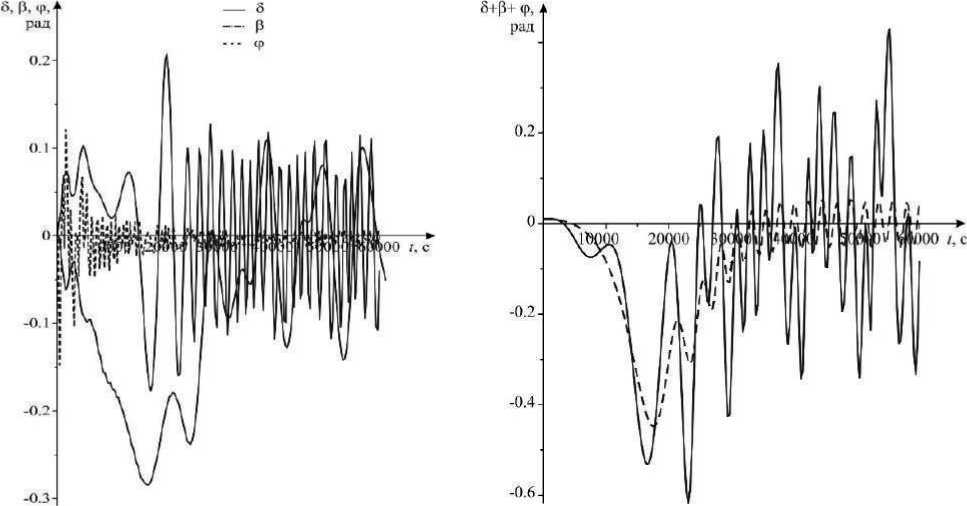
Рис. 4. Изменения углов β, φ, δ и отклонение спутника от местной вертикали (β + φ + δ) при развертывании космической тросовой системы

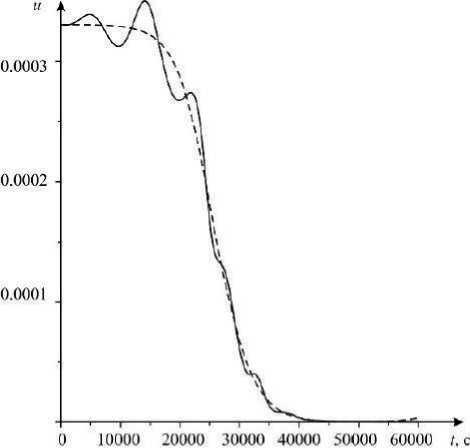
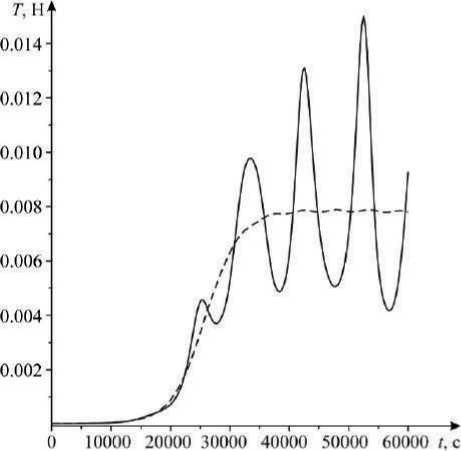
Рис. 5. График управляющей функции u_b и изменения силы натяжения троса T при развертывании космической тросовой системы

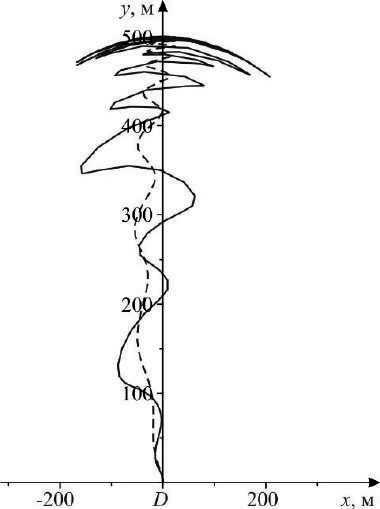
Рис. 6. Развертывание тросовой системы и орбита станции D

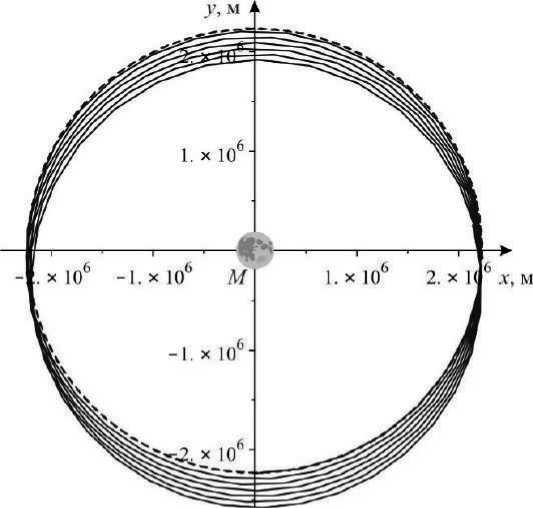
Исследуя полученные графики, можно сделать вывод, что возмущения, вызванные притяжением Земли, вызывают увеличение амплитуды колебаний спутника относительно местной вертикали.

Заключение

Рассматривалось движение космической тросовой системы, состоящей из космической станции и малого космического аппарата. Станция и спутник рассматривались как твердые тела, трос – как невесомый нерастяжимый стержень.

В работе предполагалось, что космическая тросовая система совершает радиальное развертывание по заданной программе. На движение тросовой системы оказывали влияние возмущения, связанные с притяжением Земли.

В работе получены следующие результаты:

• 1.    С помощью второго закона Ньютона и теоремы об изменении кинетического момента были составлены уравнения движения и разработана математическая модель движения космической системы.

• 2.    Был рассмотрен предложенный ранее закон управления развертыванием тросовой систе-

  
• мы и найдена сила натяжения троса, обеспечивающая требуемое управление с учетом притяжения Земли.

• 3.    Показано, что предлагаемый закон управления выпуском троса обеспечивает развертывание троса на заданную длину.

• 4.    Проведено сравнение графиков при движении тросовой системы по возмущенной и невозмущенной окололунной орбите. Из приведен-