Анализ прочности силовых элементов и металло-композитных соединений конструкции летательного аппарата

В настоящее время в аэрокосмической технике наблюдается процесс интенсивного применения высокопрочных композиционных материалов в силовых элементах и агрегатах конструкции [1; 2]. В первую очередь, этот факт обусловлен повышенными требованиями к весовому совершенству проектируемых летательных аппаратов. Как правило, в качестве основы для конструктивных силовых схем ракетно-космических аппаратов рассматривают следующие решения: подкрепленная, трехслойная и сетчатая конструкция. Характерной особенностью первых

двух подходов является то, что их основные силовые элементы (обшивка и стрингеры) не являются однонаправленными структурами, что в некоторой мере снижает их весовую эффективность [3]. В сетчатых конструкциях, основными силовыми элементами в которых являются выполненные из однонаправленного композита ребра, реализуются достаточно высокие жесткостные и прочностные характеристики при обеспечении минимальной массы. Несмотря на то, что область применения сетчатых структур ограничена регулярными зонами, их эффективность подтверждена реальными примерами реализации в конструкциях отечественных ракетоносителей [4; 5].

Применение композита в силовых конструкциях вызвало много проблем в области проектирования, производства и отработки их прочности.

Кроме того, по сравнению с изотропными материалами, слоистые композиты имеют ряд особенностей как в области деформирования, так и в области механики разрушения, которые необходимо учитывать при проектировании силовых структур [6; 7].

Одним из основных этапов в процессе проектирования летательного аппарата является этап экспериментальных исследований прочности и устойчивости на конструктивно подобных образцах (КПО), в частности, фрагментах силовых панелей. По результатам испытаний КПО опреде- ¹⁹² ляется реальная несущая способность основных силовых элементов и формируются соответствующие критерии разрушения, необходимые для оценки прочности конструкции. При предельных нагрузках в стрингерных панелях могут проявляться нелинейные эффекты, такие как местная потеря устойчивости обшивки и стрингеров. Это говорит о том, что необходимо использовать нелинейные методы расчета несущей способности панелей [8-10]. Кроме того, при проведении испытаний КПО часто возникают вопросы, насколько условия эксперимента отражают реальную работу исследуемого образца в составе конструкции и как это влияет на оценку его несущей способности. Эти вопросы рассмотрены в первой части работы на примере моделирования эксперимента по испытаниям композиционной панели на сдвиг.

Вторая часть работы посвящена исследованию прочности и устойчивости металло-композитного узла навески подвижного агрегата, который является типовым элементом и содержит многорядные болтовые соединения. Как правило, соединения представляют собой наиболее критичные места конструкции; по этой причине эффективность конструкции в значительной степени зависит от результатов их проектирования. Эта

№ 4 (34) 2020 Том 4

проблема стала еще более актуальной в металло-композитных соединениях, так как максимальная их эффективность, по данным работы [11], в лучшем случае составляет 40-50 %, а в худшем случае - значительно меньше. Для металлов эта цифра достигает величины в 70-80 %, т. е. эффективность композитов по сравнению с металлами значительно ниже. Для решения проблемы соединений в Европе была разработана программа BOJCAS (Bolted Joints in Composite Aircraft Structures) [11; 12], в которой участвуют специалисты Великобритании (Airbus UK), Германии (EADS), Швеции (SAAB), и ряда других стран. Основная задача программы – разработка и валидация новых методов расчета соединений, а также выработка критериев прочности, которые помогли бы расчетчику надежно прогнозировать прочность многоболтовых металло-композитных соединений.

1.    Анализ закритического деформирования подкрепленных композиционных панелей

В качестве объектов для расчетных исследований прочности и закритического деформирования рассматривается стрингерная панель из слоистых полимерных композиционных материалов, предназначенная для проведения испытаний на сдвиг.

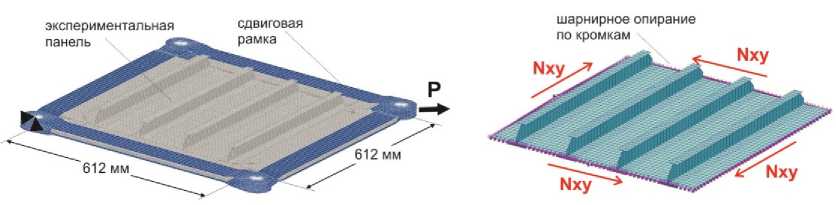
Обшивка панели толщиной 2,25 мм подкреплена четырьмя стрингерами таврового сечения толщиной 2,75 мм. Рабочая часть панели имеет размеры 612x612 мм, высота стрингера - 45 мм, шаг стрингеров - 153 мм. Материал панели - углепластик. Типовой пакет обшивки содержал 18 монослоев, а стрингера - 22 монослоя различной ориентации. На рис. 1 приведены основные геометрические параметры панели.

Рис. 1. Геометрические параметры панели

Как правило, характеристики прочности и устойчивости панели на сдвиг определяются испытаниями в сдвиговой рамке (жесткий шарнирный четырехзвенник). При испытаниях рамка растягивается вдоль одной из ее диагоналей, при этом в испытуемом образце возникает напряженно-деформированное состояние, соответствующее чистому сдвигу [6; 9; 10; 13]. Сдвиговая рамка выполнена из стальных пластин толщиной 10 мм. Пластины были соединены втулками диаметром

40 мм, обеспечивающими шарниры в углах рамки. Образец панели фиксировался в рамке двухрядным болтовым соединением с шагом 42 мм. Болты имели диаметр 6 мм. На каждое ребро рамки приходилось 28 болтов крепления образца.

Расчетные исследования по влиянию условий эксперимента на характеристики прочности и устойчивости панели при сдвиге выполнялись в программном комплексе NASTRAN. Анализ устойчивости проводился в линейной и нелиней- ной постановке задачи. Была разработана конечноэлементная модель (КЭ модель) панели и сдвиговой рамки (рис. 2а). Характерный размер расчетной узловой сетки данной КЭ модели равен 5 мм. Общая размерность модели составила 80935 узлов расчетной сетки, 77660 плоских элементов, 240 балочных и 16 элементов связи, реализующих дополнительные кинематические зависимости в угловых шарнирах сдвиговой рамки. Моделирование обшивки и стрингеров панели осуществлялось из-гибно-мембранными конечными элементами с послойным описанием структуры композиционного пакета. Такое моделирование дает возможность выполнять полноценный анализ прочности панели на основе известных характеристик монослоев и заданных критериев разрушения.

В целях сравнительного анализа были рассмотрены два варианта граничных условий. В первом случае рассматривалась панель в сдвиговой рамке, при этом реализовывались граничные условия, определяемые закреплением ее контура в эксперименте. Нагружение панели производилось сосредоточенным усилием Р, приложенным к одному из угловых шарниров, диагонально противоположный узел закреплялся от линейных перемещений (рис. 2 а ). Во втором случае рассматривалась панель шарнирно опертая по кромкам целевой зоны размером 612×612 мм. Такие граничные условия более характерны реальной работе панели в составе конструкции. Дополнительные кинематические зависимости на контуре панели обеспечивали прямолинейность ее кромок. Панель нагружалась погонными сдвигающими усилиями N_xy, приложенными по контуру панели (рис. 2 б ).

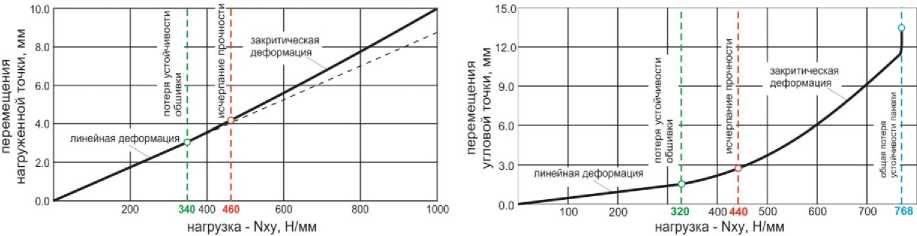
На рис. 3 показаны местные формы потери устойчивости обшивки, полученные в линейном расчете, для панели в сдвиговой рамке ( а ) и при шарнирном ее закреплении ( б ). Происходит местная потеря устойчивости обшивки панели по двум косым полуволнам между стрингерами. Получены следующие критические усилия местной потери устойчивости обшивки: N ^к_x^р_y = 340 Н/мм – для панели в рамке, N ^кр = 320 Н/мм – для шарнирно опертой панели. В данном случае, влияние условий эксперимента привело к увеличению критического усилия на ~6 %. Анализ величины действующих напряжений в панели показал, что прочность композита при этой нагрузке далеко не исчерпывается. В связи с этим были проведены нелинейные расчеты панелей с целью рассмотрения их закритического деформирования и определения величин разрушающих нагрузок.

В нелинейной постановке задача решалась итерационным методом Ньютона-Рафсона. Проведен анализ нелинейных откликов конструкции на прикладываемую нагрузку. Для панели в сдвиговой рамке под нелинейным откликом конструкции рассматривалась зависимость перемещения точки нагружения вдоль диагонали (рис. 4 а ) от уровня приложенной нагрузки:

P

Nxy = V2b , где P – приложенное усилие; b – размер рамки, а для панели без рамки – перемещения одной из угловых точек панели (рис. 4б). Эти графики дают наглядное представление об изменении сдвиговой жесткости панели в процессе ее нагружения.

а

б

Рис. 2. Расчетные модели панелей: а – панель в сдвиговой рамке; б – шарнирно опертая панель

аб

Рис. 3. Формы потери устойчивости обшивки: а – панель в сдвиговой рамке; б – шарнирно опертая панель

(оСМИЧЕскиЕ АППАРАТЫ И

Том 4

аб

Рис. 4. Нелинейные отклики конструкции на прикладываемую нагрузку:

₁₉₄                            а – панель в сдвиговой рамке; б – шарнирно опертая панель

Для шарнирно опертой панели при нагрузке N мxyпу = 320 Н/мм имеет место излом графика (рис. 4б), что соответствует усилию местной потери устойчивости обшивки. При N оxyпу = 768 Н/мм происходит резкий рост перемещений, что свидетельствует об исчерпании несущей способности панели в результате общей потери устойчивости. Для панели в сдвиговой рамке (рис. 4а) местная потеря устойчивости соответствует нагрузке 340 Н/мм, где также происходит излом графика. Далее, вплоть до нагрузки Nxy = 1000 Н/мм, других переломов и резкого роста перемещений на графике не наблюдается, что свидетельствует об отсутствии общей потери устойчивости. В дальнейшем расчет при более высоком уровне действующей нагрузки показал, что общая потеря устойчивости панели в сдвиговой рамке реализуется при нагрузке 1220 Н/мм, что более чем в 1,5 раза больше, чем для панели без сдвиговой рамки. Полученные результаты показывают, что влияние условий эксперимента на оценку общей устойчивости панели может быть значительным. При моделировании панели без рамки граничные условия соответствуют ее шарнирному опиранию, а жесткая сдвиговая рамка реализует условия, близкие к защемлению. Для панелей, спроектированных по условиям общей потери устойчивости, а не по условиям прочности, учет этого факта весьма важен.

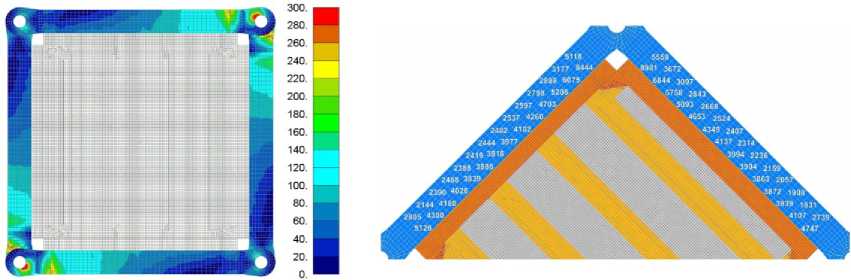
Моделирование экспериментальной рамки позволило оценить уровень напряжений в ее конструкции и болтах крепления панели. На рис. 5 а показано, что при нагрузке N_xy = 320 Н/мм максимальный уровень напряжений наблюдается в проушинах, и их величина достигает значения 330 MПa. Максимальные перерезывающие силы R б^mо^axлт = 8981 Н возникают в болтах вблизи узлов нагружения, что соответствует уровню эквивалентных напряжений в болте 275 МПа. Такие величины напряжений не являются критичными для элементов, выполненных из стали. Очевидно, что прочность в болтовом соединении рамки с панелью будет ограничиваться характеристиками на смятие композиционной обшивки, усиленной накладками.

аб

Рис. 5. Напряженное состояние сдвигой рамки ( а ) и усилия в болтах крепления панели ( б )

На основе результатов нелинейного расчета проведен анализ прочности панели. Для оценки прочности панели в качестве критерия разрушения использовался критерий Цая-Хилла [14]. Этот критерий является наиболее распространенным при расчетах прочности слоистых композитов и дает консервативную оценку [6]. Для панели в сдвиговой рамке процесс разрушения, т. е. выполнение критерия Цая-Хилла, начинается при нагрузке N Хилл = 420 Н/мм в небольшой области сопряжения обшивки и стрингера. При уровне нагрузки N Хилл = 460 Н/мм выполнение критерия происходило также в пиках образовавшихся волн потери устойчивости обшивки и в значительной области панели. Это свидетельствовало о многочисленных повреждениях монослоев обшивки, ее разрушению и исчерпанию несущей способности панели. Для панели без рамки разрушающая нагрузка соответствовала N Хилл = 440 Н/мм . На рис. 6 показано распределение зон повреждения композита (красный цвет) при нагрузках 420 Н/мм (рис. 6а) и 460 Н/мм (рис. 6б) соответственно.

а

б

Рис. 6. Распределение зон повреждения композита при закритическом деформировании панели в сдвиговой рамке

Следует также отметить, что разрушение панели происходило в закритической области ее деформирования. В линейной постановке задачи, когда потеря устойчивости обшивки не учитывалась, величина нагрузки разрушения панели по условиям прочности составляла 640 Н/мм. Очевидно, что расчетная оценка прочности данной панели на основе линейного анализа может приводить к неверному результату и завышению ее несущей способности. По результатам испытаний панели на сдвиг спрогнозированная нагрузка потери устойчивости обшивки отличалась от экспериментально полученной менее чем на 1 %, а нагрузка разрушения – менее чем на 5 %.

Результаты проведенных исследований дают возможность сделать некоторые выводы. Испытания фрагментов панелей в сдвиговой рамке дают корректные оценки критических напряжений ее местной потери устойчивости и прочности при закритическом деформировании, однако оценка критических напряжений общей потери устойчивости не всегда может оказаться корректной. Последнее связано не только с отличием граничных условий, реализуемых в сдвиговой рамке и в реальных условиях нагружения панели, но и с ограниченными размерами испытуемого фрагмента, при которых длина волны общей потери устойчивости не может реализоваться в полной мере.

2.    Анализ прочности металлокомпозитного соединения

Соединение (рис. 7) состоит из двух скошенных титановых втулок 2 и 3, которые с помощью двух хвостовых пластин через алюминиевые накладки 4 и 5 крепятся болтами к композитному ламинату 1.

Расчеты соединения проведены в программном комплексе ABAQUS, КЭ модель соединения (рис. 7) включает 499445 узлов с 1019379 неизвестными перемещениями. Для моделирования деталей соединения применялись объемные шестиузловые и восьмиузловые элементы с линейной аппроксимацией перемещений с учетом контактного взаимодействия деталей. Для лучшей сходимости решения использована опция контроля контакта с автоматической стабилизацией (коэффициент трения между деталями f = 10-4).

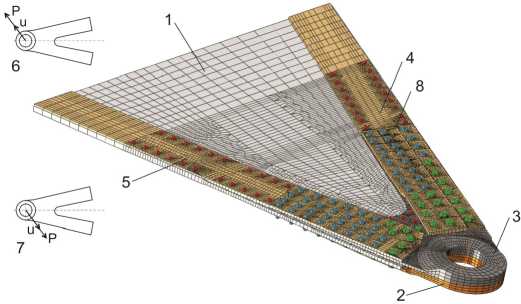
Рис. 7. КЭ модель соединения (6, 7 – случаи нагружения; 8 – зона окончания хвостовика проушин)

Модель закреплялась по торцам деталей 1, 4 и 5. Рассматривались два случая нагружения, которые условно назовем растяжением (6 на рис. 7) и сжатием (7 на рис. 7). В обоих случаях нагружения нагрузка на проушины деталей 2 и 3 передается через точку в центре проушин и специальные кинематические контактные пары, позволяющие свободно перемещаться только в направлении нагружения.

Интегральные механические характеристики многослойного композиционного пакета дета-

КИЕ АППАРАТЫ И

ТЕХНОЛОГМИ^В^И®

Том 4

ли 1 были получены по методике, приведенной в работе [15]. Расчет напряженно-деформированного состояния (НДС) проводился с учетом как геометрической, так и физической нелинейности металлических деталей соединения. Для материалов из титанового и дюралевого сплавов учет их работы в упругопластической области выполнялся на основе задания реальных диаграмм напряжений от деформаций «σ–ε».

Расчетный анализ представляет собой итерационную пошаговую процедуру, при которой перемещения центра узла на каждом шаге по-196 лучают малые приращения. При этом постепенно возрастает нагрузка, приложенная к узлу. Предполагалось, что композит в процессе нагру- жения узла не разрушается и сохраняет свои жест-костные свойства вплоть до падения нагрузки после достижения ею своего предельного значения.

На рис. 8 приводится зависимость нагрузки Р от перемещения центра проушины u. Как следует из рисунка, в случае сжатия нагрузка Р до величины перемещения u ≈ 2 мм увеличивается практически линейно, и при достижении значения 590 кН происходит общая потеря устойчивости деталей соединения. Инициатором потери устойчивости композитной пластины являются хвостовики титановых проушин (8 на рис. 7), сильно меняющие в зонах своего окончания жесткостные свойства соединения. При растяжении соединения, с увеличением нагрузки из-за нелинейности свойств металла, возникают большие деформации в зоне сопряжения проушин с их более тонкими хвостовиками, и при нагрузке 3670 кН начинается

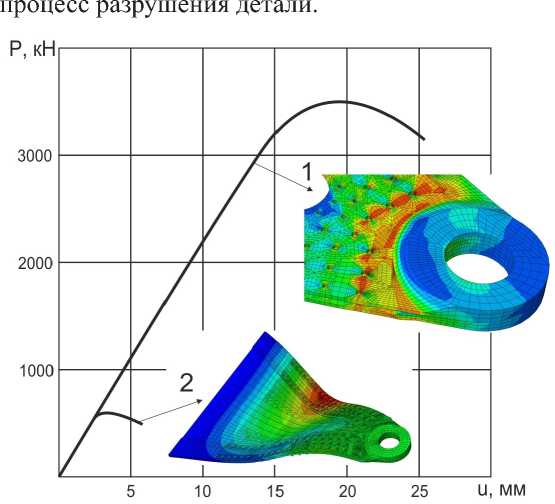
Рис. 8. Зависимость нагрузки Р от перемещения центра проушины u (1 – растяжение соединения, 2 – сжатие соединения)

Для оценки прочности композитного ламината воспользуемся критерием Нуизмера [16; 17]. Согласно этому критерию, разрушение детали с отверстием происходит тогда, когда напряжение на некотором характеристическом расстоянии r0 от контура отверстия достигнет разрушающего значения σр, определяемого выражением:

° р

σb

K d ^,

где σb – предел прочности материала, Kd – коэффициент концентрации напряжений на расстоянии r0

от контура отверстия.

Для определения характеристического расстояния воспользуемся экспериментальными данными по разрушению пластинок без отверстия и с заполненным отверстием, полученными по методикам ASTM D 6742 [18]. Разрушение пластинки без отверстия произошло при напряжении 1010 МПа, а разрушение подобной пластины с заполненным болтом отверстием (рис. 9 а ) произошло при напряжении 522 МПа. Таким образом, отверстие в пластине снизило ее прочность в K_d = 1010 / 522 = 1,93 раза. Методом конечных элементов проведен расчет квадратной пластинки с отверстием, заполненным титановой шайбой (рис. 9 б ).

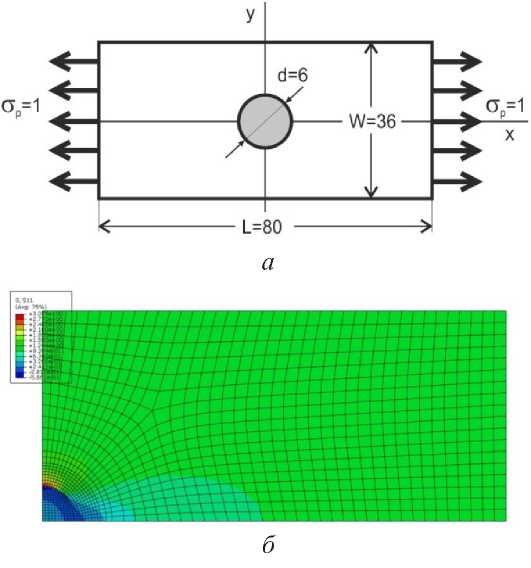
Рис. 9. Схема плоского образца с заполненным отверстием ( а ) и распределение максимальных главных напряжений ( б )

Для вычисления r0 была построена эпюра напряжений в нетто-сечении пластины x = 0 (рис. 10), и по значению коэффициента 1,93, полученному по экспериментальным данным, определено характеристическое расстояние r0 = 0,74 мм.

Анализ напряженно-деформированного состояния соединения показал, что максимальные нормальные напряжения сосредоточены по контуру болта в зоне окончания хвостовика проушин (8 на рис. 7). Используя данные расчета в этой зоне, по критерию Нуизмера прочность композита оценена в 1247 кН.

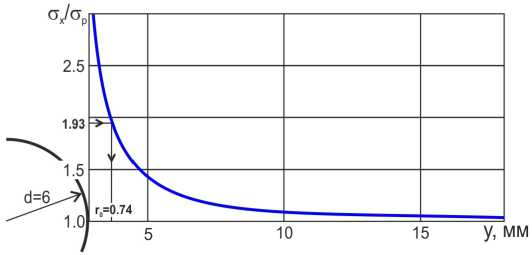
Рис. 10. Эпюра для определения характеристического размера r0

Из анализа результатов расчета соединения следует, что несущая способность соединения при его растяжении (Р = 1247 кН) значительно отличается от несущей способности соединения при его сжатии (Р = 590 кН). Также можно отметить, что металлические части соединения разрушаются при нагрузке, которая примерно в три раза превышает нагрузку разрушения композиционной детали. Наиболее простым способом повышения прочности соединения при его растяжении является замена алюминиевого сплава материала накладок (3 и 4 на рис. 6) титановым сплавом, что приведет к снижению напряжений в композите.

Если же сделать на этих деталях внешние отбортовки на четвертую часть их ширины, то можно будет повысить и разрушающую нагрузку при сжатии соединения. В дальнейшем, при экспериментальной отработке, проведенные численные исследования позволили избежать преждевременных разрушений при испытаниях соединений на прочность.

Заключение

Представленные в работе исследования еще раз показывают эффективность применения со- ¹⁹⁷ временных расчетных методов в задачах оценки прочности элементов конструкций из композиционных материалов. Они дают возможность осуществлять моделирование сложных объектов, как в геометрическом плане, так и по их физическому содержанию. Виртуальная модель эксперимента позволяет рассматривать испытуемый объект, а также элементы нагружающих устройств и оснастки, используемых при испытаниях. Расчетное сопровождение экспериментальных работ с использованием методов виртуального моделирования является основой не только для валидации расчетных моделей, но и для прогнозирования условий работы объекта испытаний в системе конструкции.