Анализ пространственных характеристик четырёхволнового преобразователя излучения на тепловой нелинейности в схеме с попутными волнами накачки

Важнейшей характеристикой любого четырехволнового преобразователя излучения является точность, с которой он осуществляет преобразование комплексной амплитуды падающей на него волны. В линейном приближении по амплитудам сигнальной и преобразованной волн полной характеристикой точности преобразования амплитуды сигнальной волны может выступать функция размытия точки (ФРТ) [1,2]. Использование тепловой нелинейности позволяет расширить класс веществ, применяемых для обращения волнового фронта, за счёт сред с линейным коэффициентом поглощения, которые не обладают выраженными нелинейными свойствами нетеплового характера [3]. Для среды с тепловым механизмом нелинейности в [4] найдена и проанализирована ФРТ четырехволнового преобразователя излучения в схеме со встречными волнами накачки. Переход к схеме с попутными волнами накачки позволяет создать волну с обращённым волновым фронтом распространяющуюся в направлении сигнальной волны [5], поэтому не меньший интерес представляет анализ пространственных характеристик четырехволнового преобразователя излучения на тепловой нелинейности в схеме с попутными волнами накачки.

1. Вывод основных уравнений, описывающих четырехволновое взаимодействие

Пусть в плоском слое с тепловой нелинейностью толщиной t распространяются две волны накачки с комплексными амплитудами A 1 и A и сигнальная волна с амплитудой A ₃ . В результате вырожденного четырехволнового взаимодействия ю + ю-ю = ю генерируется преобразованная волна с амплитудой A ₄ (рис. 1).

Стационарное волновое уравнение, описывающее такое взаимодействие, имеет вид

{V2 + [ к2 fl + — — 5 T1- ndT fV 4    °     )                                 (1)

- 2 ik a ]} I У Aj- + к .с . I = °.

I j =1 J

Здесь n ° - среднее значение показателя преломления, к - волновое число, a - коэффициент поглощения, 5 T - изменение температуры, обусловленное выделением тепла при поглощении излучения.

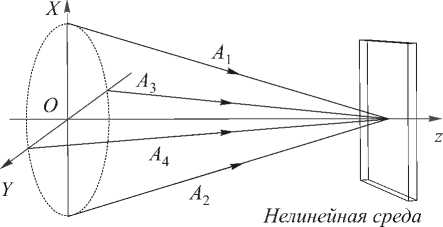
Рис. 1. Схема четырехволнового взаимодействия с попутными волнами накачки

Уравнение (1) необходимо дополнить уравнением Пуассона

V25 T +

a

^Л c p ^v

У A J + к-с .

j =1

= °,

где Л - коэффициент теплопроводности, c p - удельная теплоемкость, v - объемная плотность вещества.

Будем рассматривать четырехволновое взаимодействие в приближении заданного поля по волнам накачки (| A 1 ₂12 >>  A ₃₄| 2 ). При условии, что коэффициент преобразования мал (| A ₃|² >>  A ₄|²), в выражении для интенсивности взаимодействующих волн необходимо учитывать только решетки, образованные при интерференции волн накачки с сигнальной волной

У A j + к с .

j =1

= У A j A * + A 1 A * + A ₂ A * + A * A ₃ + A ₂ A ₃.

j =1

Изменение температуры представим в виде суммы трёх слагаемых:

5 T = 5 T° + 5 T31 + 5 T32, одно из которых 3T° связано с распространением в среде волн накачки, а два других ЗТ31 и ЗТ32 с интерференцией волн накачки с сигнальной волной.

Разложим составляющие изменения температуры S T 3j по гармоническим решеткам

⁵ T 3j (r) = J 5 T 3j ( K Tj , z )exp( — i К Tj -P) d К Tj , j = 1,2.

Здесь 5 T₃ j - амплитуды спектров тепловых решеток, записанных сигнальной волной и j - ой волной накачки, р ( x , y ) - поперечная составляющая радиус-вектора r , к _Tj - пространственный вектор гармонической решетки.

Пусть волны накачки являются плоскими волнами

A j (r) = A j o ( z )exp { — i ^—j P — ik jz z } ,            j = 1,2.

Падающую волну разложим по плоским волнам

A 3 ( r) = J A 3 ( K 3 , z ) exp { — i к 3 P — ik 3 _zz } d K 3 .

Учитывая наличие в нелинейной среде двух тепловых решеток, представим преобразованную волну в виде суммы двух волн A 4 = A ₄₁ + A ₄₂, каждую из которых также разложим по плоским волнам

A4m (Г) = J A4m (K4m , z)eXP {— iK4mP — ik4mzz} dK4m , m = 1,2.

Здесь K j и K _{4 m} , k_jz и k _{4 mz} - поперечная и продоль-

—*

——

ная составляющие волновых векторов k _j и k _{4 m} , j = 1 ^ 3, m = 1,2, k j | = | k 44 _m | = k . Направления осей OX и OY выберем таким образом, чтобы ось OX лежала в плоскости, образованной волновыми векторами волн накачки (плоскость волн накачки), а ось OY в плоскости, перпендикулярной плоскости волн накачки.

Учитывая сделанные выше предположения и в приближении медленно меняющихся амплитуд, волновое уравнение (1) распадается на пять уравнений вида dAj 0 . k f k dn .     ,           _ 1 ->

+ i — 15 T — i a A4m — 0, j —1,2, dz     kjz [ n 0 dT 0 j j 0

dA ₃ (K₃, z ) . k I k dn . I -

---Л----⁺ i y-1—-T^^{5 T} 0^{( z} ) ^— i 4 ^A 3^{( k} 3 , ^z ) = ⁰

dz         k3, I n0 dTI

"W dA41 (K41 , z)

dz k2 dn k41z n0 dT

k I k dn , . I ~.

+ i",---1—    5 T0(z ) - i аГ A41 (K41, z) = k41 z L n0 dTj

^{5 T} 31 ^{( K} T 1 = ^K 41 ^-K 2 , ^z ) ^X

x A ₂₀ ( z )exp { — i ( k 2 ^

dA ₄₂( K ₄₂, z )   . k I k dn

dz k2 dn

5 T ₃₂( K _{T 2} = K ₄₂ -K ₁, z ) x

^k 42 z L n 0 ^dT

5 T o ( z ) - i аЛ A 42 ( K 42 , z ) =

A j0 ( z = 0) = A ⁰0 0 ,

A 3 ( K 3 , z = 0) = A 0 ( K 3 ),

"A 4 m ^{( K} 4 m , z = ⁰⁾ = ⁰.

Уравнение Пуассона распадается на три уравнения d-^T0- + -^ (A10 (z)A;0 (z) + A20 (z)A20 (z)) = 0, (8) dz    Л cp vv’

Г d2     2

I "TT ^+K Tj I^{5 T} 3 j ^{( K} Tj , ^z ) =

(dz)

= —7^- Aj0 ^A3 (K3, z)exP {— i(kjz — k3z )z} ,        (9)

Л cp v                    v j j j = 1,2.

При выводе уравнений (3)-(6), (9) считали, что k_{t 1} = t^- ₁ — 1< ₃ = /К₄₁ — 1< ₂, K— T ₂ = i< ₂ — K— 3 = k₄₂ — k_v

При условии отвода тепла от передней и задней граней нелинейной среды ( 5 T ₃ j ( K _Tj , z = 0) = = 5 T ₃ j ( K _Tj , z = / ) = 0) с учетом граничных условий (7) решения уравнений (3)-(4), (8) можно записать следующим образом:

A 0 ( z ) = A"_oexp { —a z — iC ( z ) } , j = 1,2,        (10)

A ₃( K ₃, z ) = z 4 ₃⁰( K ₃)exp { —a z — iC ( z ) } ,            (11)

5 T 0 ( z ) =

TT— E ( A 0 0 )² 4 аЛ C p v j :1

X

X 1 — exp(—2az)— z [1 — exp(—2a^)] , где C(z) = —dnj5T0(z1)dz1 .

n ₀ dT ₀

С учетом изменения вдоль оси Z амплитуд волн накачки и сигнальной волны уравнение (9) имеет решение вида

5 T 3 j ( K Tj , z ) =

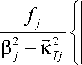
-------X

2 sh к Tj i x {exp(—K Tjz) |^exp(K Tj i) — exp(—p ji)]}

1                                               (13)

+ —--- "{ exp^{( K} j ) [ exp^{( —}P j ^{i ) —} exp^{( —K} Tj ⁱ ) 1 }

2 sh к _Tj i^{1           L}

- ^exp⁽ —P j^z )

Здесь f = ^a A j^ ^4° ( K 3 ) ]/л C p v , P j = 2 a + i ( k_jz — k _{3 z} ).

^K Tj I ^K Tj I ,

Подставив (13) в (5-6), получим с точностью до постоянного множителя выражения для пространственных спектров амплитуд преобразованной волны на задней грани нелинейного слоя

AV

A4j (K4j = Kj - K3 , Z = t) = fj    I 1    [exp(-Pjt) - exp(K Tt)]

P 2 -k Tj 1 2 sh к _Tj t        [ к _Tj + ip_j ]

x [exp( -K _Tj t - ip j t ) - 1] +

X

1    [exp( -P j t ) - exp( -K t )]

+--------------------------X

² sh ^K j       ^{[ K} Tj

- iP j ]

x [exp( K _Tj t - ip j t ) - 1] +

exp(-P jt - ipjt) -1 Pj + ipj где p, = (k2z - k41 z), p2 = (k1z - k42z). В параксиаль- ном приближении при условии, что волны накачки падают на нелинейную среду под одинаковыми уг- лами (K1 =

^-к2 ) : p j = 2 k ^(K4 j

^^^^^^в

^к 2 ).

На рис. 2 при условии A 100 = A 20 приведён характерный график зависимости модуля коэффициента преобразования

L A 4j ^{( K}4 j =^K j -^K I " Z = ^f )

^{K ( K} з ) =  ----- A^------ ^<15)

от поперечной составляющей волнового вектора сигнальной волны.

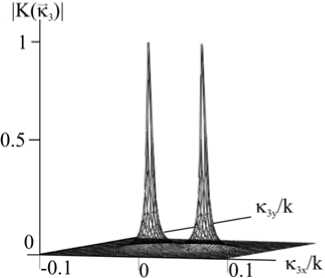
Рис. 2. Вид модуля коэффициента преобразования при угле между волнами накачки 6 ° и a t = 1,44

На графике зависимости модуля коэффициента преобразования от K 3 наблюдаются два максимума, расстояние между которыми прямо пропорционально углу между волнами накачки. Наличие двух максимумов связано с записью в нелинейной среде двух тепловых решеток. В сечении максимумов плоскостью, параллельной плоскости к ₃ x к ₃ y по уровню 0,5 от максимального значения, наблюдаются кривые, напоминающие эллипсы. Большая ось эллипса расположена в плоскости волн накачки и направлена по прямой, соединяющей максимумы. Величины малой и большой осей эллипса зависят от величины коэффициента поглощения и волнового числа.

При возрастании волнового числа большая и малая оси эллипса возрастают. При k = const и росте коэффициента поглощения малая полуось эллипса уменьшается, а большая - возрастает.

Фаза коэффициента преобразования в зависимости от K 3 меняется по закону, близкому к параболическому. С ростом коэффициента поглощения скорость изменения фазы увеличивается, а при возрастании волнового числа – уменьшается.

• 2 . Функция размытия точки

Пусть сигнальная волна распространяется от точечного источника, расположенного на расстоянии z ₃ от передней грани нелинейного слоя (плоскость фокусировки сигнальной волны). Тогда с точностью до постоянного множителя комплексная амплитуда сигнальной волны на передней грани нелинейного слоя есть

.                         . . к

A 3 ^{( k} 3 , ^z = 0) = ^exp^{( -} i ^к з Р ₀ ⁺ i — ^z 3 ) , 2 k

где р ₀ - вектор, определяющий положение точечного источника в плоскости z ₃ .

Будем рассматривать поле преобразованной волны на расстоянии z ₄ от задней грани нелинейного слоя (плоскость фокусировки преобразованной волны)

к

A 4j ^{( к} 4 j , ^Z 4 ) = A 4j ^{( K}4j , ^Z = ^{t )} exp⁽ i "TTz 4 ) .       ⁽¹⁷⁾

2 k

Под четырехволновым преобразователем излучения будем понимать оптическую систему, состоящую из участка свободного пространства толщиной z ₃ , среды с тепловой нелинейностью, в которой распространяются две волны накачки, и участка свободного пространства толщиной z ₄ .

Функция размытия точки является Фурье-образом от амплитуды пространственного спектра преобразованной волны на выходе оптической системы при условии, что на ее входе оптический сигнал является точечным

Г ( р , z 3 , z 4 ) = [ A 41 ( K 41 , z 3 , z 4 )exp( - i к 41 P ) d K 41 +

+ J A 42 ( K 42 , z 3 , z 4 ) exp( - ¹ K 42 P ) d K 42 .

Подставив (14) в (18), с учетом (16), (17) получим выражение для функции размытия точки четырехволнового преобразователя излучения на тепловой нелинейности с попутными волнами накачки в центре поля зрения ( p ₀ = 0) в виде

Г ( р , z , z ₄) = f У ₂^fj° ₂ 1--- ¹--- x

• ^{3    4    J} j =1 P 2 -K ^[ 2 sh к T t

^[exp^{( -}P j ^{t ) - e}xp^{( K} Tj ^{t )]} x

[exp( -K _Tj t - ip_а t) - 1] +

^{[ K} Tj ⁺ ip j ]

^{[ k} Tj ^-

ip_j ]

exp( -P ₇ t - ip /) -11

-----------1--------^J- --------lx

x [exp( K _Tj t - ip_} t) - 1] +

-

P j + ip j

i K ₄ j р d K _4j

Здесь f j 0 = a A ” 0 /Л c p v . На рис. 3 приведен характерный график зависимости от поперечных координат нормированного на максимальное значение ( Г _max ) модуля функции размытия точки Г ( р ) = Г ( р )| / Г max , полученный методом численного анализа выражения (19). С ростом поперечной координаты наблюдается уменьшение модуля ФРТ.

Г(р)

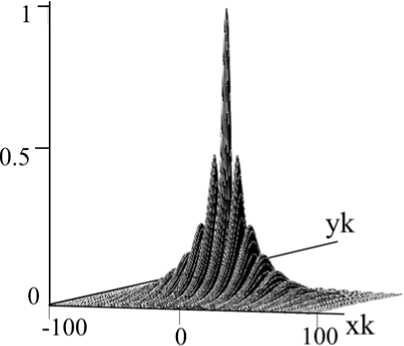
Рис. 3. Вид модуля ФРТ при угле между волнами накачки 6 ° и a t = 1,44

Введем понятие ширины модуля ФРТ в плоскости волн накачки ( А х = x - х 2 1) и в плоскости, перпендикулярной плоскости волн накачки ( А у = У - у 2| ), где х 1 2 и у , 2 , определяются из условий

|Г ^{( х} 1,2 , У = 0, z 3 , z 4 )| = 2 1 Г ⁽ Р = 0, z 3 , z 4 )| ,      (20)

| Г ⁽ У 1,2 , x = 0, z 3 , z 4 )| = 21 Г ⁽ Р = 0, z 3 , z 4 )| .      ⁽²¹⁾

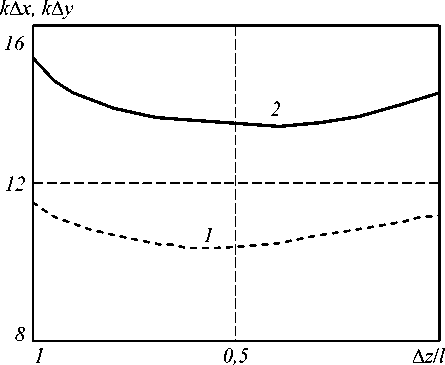
Рис. 4. Изменение ширины модуля ФРТ в плоскости волн накачки (1), в плоскости, перпендикулярной плоскости волн накачки (2) при угле между волнами накачки 3 ° и a t = 1,44

Ширина модуля ФРТ характеризует разрешающую способность четырехволнового преобразователя излучения. На рис.4 приведены зависимости ширины модуля ФРТ от разности положений плоскостей фокусировки сигнальной и преобразованных волн: A z = z ₃ - z ₄ .

При фиксированном положении плоскости фокусировки сигнальной волны существует оптимальное положение плоскости фокусировки преобразованной волны (плоскость оптимальной фокусировки), в пределах которой ширина модуля ФРТ минимальна. Положения плоскостей оптимальной фокусировки преобразованной волны при рассмотрении ширины модуля ФРТ в направлениях, задаваемых осями ОX (z4opt//) и OY (z4opt±), различно. При малых углах к j падения волн накачки на нелинейную среду — << 1 k и at < 1 положение плоскостей z4opt± и z4opt// совпадает и определяется выражением вида

t z4opt 1 z4opt// z3 + n ■                                 (22)

С увеличением угла между волнами накачки наблюдается резкое уменьшение ширины модуля ФРТ в плоскости волн накачки и незначительное изменение ширины модуля ФРТ в плоскости, перпендикулярной плоскости волн накачки (рис.5, кривые 1,2). При этом увеличивается и расстояние между плоскостями оптимальной фокусировки z _{4 opt //} и z 4 opt ± (рис. 5, кривая 3). С физической точки зрения сужение модуля ФРТ в плоскости волн накачки аналогично уменьшению ширины пятна при дифракции Фраунгофера на двух отверстиях с ростом расстояния между отверстиями.

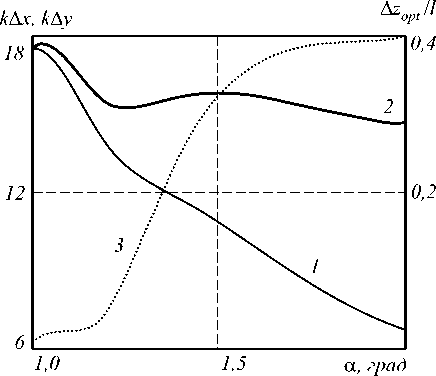
Рис. 5. Зависимость ширины модуля ФРТ в плоскости волн накачки (1), в плоскости, перпендикулярной плоскости волн накачки, (2) и расстояния между плоскостями оптимальной фокусировки A Z_opt = A z op _± - A z _opt|| (3) от угла между волнами накачки при a t = 1,44

На рис. 6 приведены зависимости ширины модуля ФРТ в плоскостях оптимальной фокусировки z 4 opt // и z 4 opt i (кривые 1, 2) и относительного положения этих плоскостей A z // = ( z 4 opt // - z 3 ) Jt и A z _± = ( z 4 opt _± - z 3 ) Jt (кривые 3,4) от толщины нелинейного слоя. При at >  1 увеличение толщины нелинейного слоя приводит к относительному сдвигу положения плоскостей оптимальной фокусировки к нелинейному слою. При этом ширина модуля ФРТ в плоскостях оптимальной фокусировки z ₄ opt // и z ₄ opt _± изменяется по закону

Ax = Р, Vt, Aу = Р2 Vt .

Здесь Р j - коэффициенты, P j > Р ₂. Величина коэффициента р , возрастает с увеличением угла между волнами накачки.

В заключение приведем оценки ширины ФРТ четырехволнового преобразователя излучения на тепловой нелинейности в схеме с попутными волнами накачки. В качестве нелинейной среды рассмотрим CCl ₄ , в которой распространяется излучение CO ₂ -лазера ( a = 18 см "1, n = 1,46) [6]. При толщине нелинейной среды t = 500 мкм , и угле между волнами накачки 2,3 ° ширина ФРТ в плоскости волн накачки A x = 12 мкм , в плоскости, перпендикулярной волнам накачки A у = 15,5 мкм . Приведённые значения получены в плоскости оптимальной фокусировки.

Для сравнения отметим, что в случае четырёхволнового преобразователя излучения на тепловой нелинейности в схеме со встречными волнами накачки, при условии A z = 0 [4] ширина модуля ФРТ равна 10 мкм.

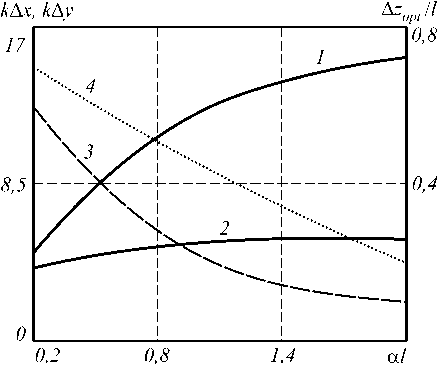
Рис. 6. Зависимость ширины модуля ФРТ в плоскостях оптимальной фокусировки z4opt// (1)

и z4opt± (2) и относительного положения этих плоскостей(3,4) от толщины нелинейного слоя при угле между волнами накачки 6°