Анализ псевдоголографического метода с точки зрения р-адических метрик

Впервые опубликованная в работах [1, 2] идея псевдоголографического кодирования, заключается в том, что отсчеты цифрового двумерного массива (цифрового изображения) переупорядочиваются специальным образом, так что по любой части переупорядоченного массива можно реконструировать уменьшенную копию исходного изображения. Закодированное изображение (псевдоголограмма) имеет «шумоподобный» вид.

Среди преимуществ метода, отметим основные.

Псевдоголографическое представление изображения позволяет, даже при потере некоторого блока информации, восстановить полное изображение. Погрешность восстановления при этом будет зависеть от объема потерянной информации, тогда как при обычном методе хранения и передачи изображения потеря блока будет безвозвратной, то есть приведет к утере фрагмента [8].

Псевдоголографическое представление изображения оказывается эффективным в ситуациях, когда положение информационного блока, пришедшего на вход, оказывается неизвестным, то есть, возможно, восстановление изображения по произвольной части кодирующей подпоследовательности даже при отсутствии информации о положении данной подпоследовательности [8].

Данный метод кодирования изображения предоставляет возможность последовательного уточнения восстановленного изображения в распределенных сетях. Можно сказать, что пользователь может сам выбирать то соотношение времени и качества, которое его устраивает.

Представление изображения с использованием данного метода таково, что разложение изображения обладает неким декоррелирующим свойством, что позволяет использовать его в задачах фильтрации коррелированного импульсного шума при передаче данных по зашумленному каналу.

Суть регулярного метода псевдоголографического кодирования

Идея метода псевдоголографического представления данных заключается в том, что двумерный массив точек изображения разворачивается в одномерную последовательность по определенному правилу. При этом каждой точке на изображении ставится в соответствие не только пара координат (m,n)

- адрес точки в двумерном массиве, но и некоторое число - к , которое и определяет номер данной точки в кодируемой последовательности.

Переупорядочивание отсчетов осуществляется специальным образом по заранее выбранному пользователем правилу. Псевдоголографическое преобразование характеризуется следующими параметрами: р , N .

Пусть исходное изображение имеет размер p ^N х p N , где p - простое число. Рассмотрим основные положения на примере р =2, а N =8. Правило нумерации задается произвольно, пример приведен на рис. 1.

0	2
3	1

Рис. 1. Правило нумерации

Обозначим матрицу, изображенную на рис. 1, буквой A . Количество строк и столбцов этой матрицы должно быть одинаковым и равно р . Это соответствует элементарному изображению р х р , (изображению наименьшего размера).

Дополнительные функции, по которым и будет в дальнейшем определяться нумерация точек, задаются формулой:

A X ( к ) = n , существует m : A ( m , n ) = к ,

A Y ( к ) = m , существует n : A ( m , n ) = к .

Для заданного значения параметра р =2 и правила нумерации дополнительные функции определяются как показано на рис. 2. Здесь в первой строке перечислены значения к - аргумент функции, а во второй - значения n и m, соответственно, - значение

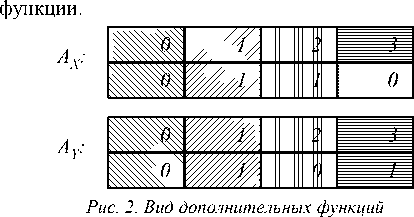
Пусть (m,n) - пространственные координаты отсчета на изображении, к - номер данного отсчета в получаемой последовательности { h_t } , где к = 1, PN (PN=p^N хp ^N ) .

Начальный уровень нумерации (N=1) определяется правилом нумерации, следующие уровни (N=2 и N=3) имеют вид, представленный на рис. 3 a , б .

0	8	2	10
12	4	14	6
3	11	1	9
15	7	13	5

0	32	8	40	2	34	10	42
48	16	56	24	50	18	58	26
12	44	4	36	14	46	6	38
60	28	52	20	62	30	54	22
3	35	11	43	1	33	9	41
51	19	59	27	49	17	57	25
15	47	7	39	13	45	5	37
63	31	55	23	61	29	53	21

а)                             б)

Рис. 3. Уровни нумерации

Правило нахождения пространственных координат отсчета (m,n) по его номеру k в кодируемой подпоследовательности определяется по формуле :

N - 1

n = Z p ^{N - 1 - 2} A x

2 = 0

Г k

'

m =

J- p ^{2 2}

(mod

N - 1

Z p i=0

- N ^{- 1 -} i A Y

k

I- p ^{2 2}

(mod

^

P 2 ) , J

^

P 2 )

J

где [d] означает целую часть числа d.

Нахождение номера отсчета k в кодируемой по-

которые могут принимать значения от 0 до p^{N 1} - 1. Далее, сопоставляя таблицы функций A_X и A_Y , получаем q ( i ) , как число, находящееся в матрице А , имеющее координаты (m₂ , п₂) . Значение k_N - 1 определяется из последнего локализованного квадрата размером р x р .

Анализ метода псевдоголографического кодирования с точки зрения р-адических метрик

К вопросу о нумерации точек исходного изображения для получения выше описанной последовательности можно подойти с точки зрения р -адического расстояния.

Пусть р – простое число, тогда любое число n ( п е Z ) можно представить следующим образом:

п = p ^a m ,                                    (4)

где а = v_p(n) - p -адический показатель числа п , а НОД( р,m )=1.

Тогда р -адическая норма числа n определяется по формуле:

II n p = p ^^Vp(n) ,                                         (5)

следовательности по его пространственным координатам (m,n) осуществляется по формулам:

k i = k i + i ■ p ^{2 +} q ( ² ),

q ^{( 2} ) = Q ⁽ m, ni,² , p , N ),                            (3)

k N - 1 = A ⁽ m ^- n ^)-

I = 0, N - 2;

причем

101 p = 0- а

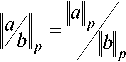
Для одномерного случая p -адическое расстояние между n ₁ и n ₂ определяется по формуле:

d p ( ⁿ 1 ^,n 2 ) = || n 1 ^{- n} 2|| _p

mi = mi-1 (mod pN i) n, = п,-1 (mod pN-i), < mо = m, n 0 = n i = LN-", где q(i) – это номер квадрата, имеющий размер N-1-i N-1-2

p x p , в который попал отсчет с пространственными координатами (m,n) на i -ом уровне кодирования; k ₀ – значение номера отсчета k в кодируемой последовательности; k_i – промежуточное значение k . Функция Q ( m_i , n_i , i , p , N ) определяет номер квадрата q ( i ) по координатам (m_i , n_i) , функциям A_X и A_Y и вычисленным по значениям р, i и N границам квадратов следующего (более высокого) уровня кодирования: в выбранном квадрате с номером q ( i - 1) определяется положение искомого отсчета. Для этого рассчитывается пара новых «приведенных» координат (m_i , n_i) в заданном квадрате,

Для двумерного случая существует два типа норм:

1) (x,y) ^е Z ² ,

II⁽ xy ) p,d = x ² - ^{dy 2} 1 l _p ’                                (7

полагая d=-1 , получаем:

II⁽ x - y )l I p = J x ^{2 +} y ² 1 I p^;

²⁾ l⁽ x,y ⁾l p,_z =1 x ± Y-\p -

(7’)

В работе А.М. Брукштейна [1] рассматривается, фактически, покрытие областями, заданными на изображении шарами уменьшающихся 2–адических диаметров, понимаемых в смысле 2–адической метрики (7’).

В данной работе рассматривается метод кодирования, соответствующий второму типу норм (8). Порядок нумерации приведен для р =3 и γ =1.

Итак, пусть р =3 и γ =1, тогда формула (8) примет вид:

||⁽ x,y ) 3 = || x + j | ^- ⁽⁹⁾

Нумерация точек исходного изображения для получения выше описанной последовательности будет иметь следующую структуру. Определим две независимые нумерации: нумерацию шаров и нумерацию точек в шаре.

Пусть правило нумерации имеет вид, представленный на рис. 4.

8	2	4
5	7	1
0	3	6

Рис. 4. Пример правила нумерации для р=3

При этом дополнительные функции примут, вид изображенный на рис. 5.

0	1	2	3	4	5	6	7	8
0	2	1	1	2	0	2	1	0

0	1	2	3	4	5	6	7	8
0	1	0	2	0	1	2	1	0

Рис. 5. Вид дополнительных функций для заданных параметров

Определим шары целого радиуса (не больше 1/2). Таких шаров будет три, они определяются из формулы (9) и представлены на рис. 6. В каждой таблице маркером отмечены отсчеты, принадлежащие соответствующему шару (первая таблица – ша-

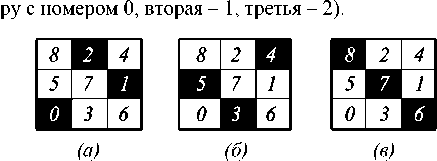
Рис.6. Распределение отсчетов изображения по соответствующим шарам:

• (а)    – отсчеты, принадлежащие шару с номером 0,

• (б)    – отсчеты, принадлежащие шару с номером 1, (в) – отсчеты, принадлежащие шару с номером 2

Определим нумерацию точек в шаре. Пусть, в данном случае, точки будут нумероваться в следующим порядка: нулевая точка каждого шара находится на второй строке таблицы на рис. 4, первая на первой, вторая – на нулевой. Такое представление изображено на рис. 7. Запись S _i ^{( j)} означает, что отсчет, находящаяся на этом месте принадлежит шару с номером i и имеет в нем внутренний номер j .

S™		s™
S™	S^	c(l)
S^	S^

Рис. 7. Нумерация самих шаров и точек в них

Аналогично, дополнительным функциям определяется нумерация в таблице 1.

Таблица 1. Дополнительная функция В(Ni,j)

Ni номер точки	Nc номер шара, j =1	Ncс номер точки в шаре, j =2
0	0	0
1	0	1
2	0	2
3	1	0
4	1	1
5	1	2
6	2	0
7	2	1
8	2	2

Итак, теперь каждая точка с номером n будет иметь двойную нумерацию: а 1 ,в 1 ,а₂,в₂,а₃ , , где а 1 - номер самого большого шара (самый высокий уровень), в 1 — положение точки в нем и так далее, от большего шара к меньшему.

Анализ формирования рассматриваемой нумерации приводит к формуле зависимости номера точки последовательности и ее адреса (см. формулу 10):

N i =

k

(p ² )

(mod p ² ),

- Nci = B(Ni1),

Ncci = B(Ni, 2 ),

i = 0 ,N - 1 .

Пример 1. Определение адреса отсчета изображения по номеру в кодируемой последовательности.

Определим адрес отсчета с номером 52 для изображения с нумерацией, представленной на рис. 8, р =3, N =2.

80	26	44	74	20	38	76	22	40
53	71	17	47	65	11	49	67	13
8	35	62	2	29	56	4	31	58
77	23	41	79 1	\ 25	43	73	19	37
50	68	14	G®9	70	16	46	64	10
5	32	59	7 I	\ 34	61	1	28	55
72	18	36	75	21	39	78	24	42
45	63	9	48	66	12	51	69	15
0	27	54	3	30	57	6	33	60

Рис. 8. Нумерация отсчетов изображения размера 9×9

Из (10) следует, что:

1) N 0 =	52 _ 1	(mod 9 ) = 7
f B( 7 , 1 ) = 2 , [ B( 7 , 2 ) = 1 ,		J a 1 = 2 , ^t в 1 = 1 ;
2) N 1 =	" 52 " _ 9 _	(mod 9 ) = 5 ;
f B( 5 , 1 ) = 1 , [ B( 5 , 2 ) = 2		f a 2 = 1 , ^l e 2 = 2 .

Следует отметить, что первоначальную нумерацию шаров изображения р х р и положения в них можно выбирать произвольным образом, нумерация k к шаров на изображении р х р однозначно определяется этой первоначальной нумерацией.

Из всего описанного выше можно сделать вывод о том, что точки с соседними номерами в кодируемой последовательности лежат максимально далеко друг от друга на исходном изображении ( р -адическое расстояние минимально). Это обусловливает декоррелирующее свойство последовательности, следствием которого являются преимущества псевдоголографического представления данных, изложенные во введении.

Декоррелирующее свойство псевдоголографического преобразования

Как уже говорилось ранее, данное преобразование изображения обладает некоторым декоррелирующим свойством [5].

Если кодируемое изображение имеет размеры 2 к х 2 к и р - коэффициент корреляции этого изображения ( р е ( 0 , 1 ) ). В результате кодирования данного изображения получаем одномерную последовательность его отсчетов. При чем минимальное расстояние на изображении между двумя соседними отсчетами последовательности равно 2 к ^{- 1} . Для би-экспоненциальной корреляционной функции оно определяется соотношением:

Р = Р к - 1 .                                     (11)

Пусть исходное изображение имеет размер 256 x 256 ( к =8), р =0,9 (среднее значение р для реальных изображений), тогда p_max = 1 , 4 - 10 ⁶ .

Отметим, что говорить о полном декоррелирующем свойстве некорректно, однако данный результат говорит о возможности применения данного свойства в задачах передачи и обработки изображения.

Итак, пусть изображение передавалось по информационному каналу при воздействии импульсного шума. Если импульсный шум был случайным, то он останется случайным и после восстановления.

Однако если он был коррелированным (группированным), то после восстановления он равномерно распределится по изображению (так как при кодировании используется кодируемая последовательность, то любая ее подпоследовательность равномерно распределена по всей области изображения; соседние отсчеты находятся на расстоянии не меньше 2 к ^{- 1} ). В этом случае, шум после восстановления становиться локально-некоррелированным, что упрощает задачу фильтрации.

Работа выполнена при поддержке Министерства образования и науки РФ, правительства Самарской области и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), а также при поддержке гранта Президента РФ № НШ-1007.2003.01 и гранта РФФИ №05-01-96501.