ВВЕДЕНИЕ.                       1) частица полагается жесткой;

ПОСТАНОВКА ПРОБЛЕМЫ

• 2)    тепловые эффекты не рассматриваются;

В статье [1] выделены и проанализированы основные работы, посвященные качественному обзору публикаций, относящихся к расчету радиационного давления в идеальных жидкостях и в случае малых волновых размеров пограничного слоя вокруг включения. В настоящей публикации рассматриваются работы, в которых так или иначе учитывается вязкость и теплопроводность окружающей жидкости.

Указанные вопросы в основном систематически рассматривались в сериях статей, принадлежащих трем различным группам авторов. Это А.Н. Гузь и А.П. Жук, С.Д. Данилов и М.А. Миронов, а также А.А. Дойников, что нашло отражение соответственно в работах [2–6], [7–10] и [11–15 ], а также в ряде других работ этих авторов. Соответственно в работах [6], [10] и [11] авторы делают обзоры по заявленной тематике, причем в работах [10] и [11] авторы критикуют подходы друг друга, не приходя к единому мнению относительно полученных результатов.

Целью настоящей статьи является анализ упомянутых трех серий публикаций, выявление допущений и пренебрежений, принимаемых в этих работах.

РЕШЕНИЕ ЗАДАЧИ

• 1.    Анализ начнем с работ [2–6], авторы которых в работе [2] делают следующие допущения, остающиеся далее неизменными во всех оставшихся цитируемых здесь работах этих авторов:

• 2.    Остановимся на анализе работ [7–10]. В работе [7] и далее в остальных работах [8–10] этой группы авторов в качестве базового принимается выражение для силы радиационного давления (СРД) в виде среднего потока импульса через произвольную замкнутую поверхность, охватывающую частицу

  а

  
  

  u A l T = 0

  
  
  
  
  
  
  

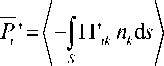
  Здесь и = — — коэффициент кинематической ρ ₀

  вязкости.

  Акустическое давление с точностью до величин второго порядка малости представляется выражением [2]

  
  

  Г

  = Н Р ^ д ⁺ P V i v k ^— —

  
  

  S

  
  

  k

  
  

  - C^ k i v¹ a x ;

  
  

  n_k d s .

  
  

  Г 4 a ⁵ V 1 р ₀<аФ^ p = р₀ u AФ +

  ⁰ (З      St)    2с₀2 (аг)

  
  

  —

  
  

  1           4 Po дФ

  — p ( VФ) — и 0- АФ .

  2 ^0V ’    3 c ₀ ² a t

  
  
  
  

  Тогда гидродинамическая сила F на твердом теле с поверхностью S вычисляется по формуле [2]

  
  

  F = j T - n d s .. S

  
  
  
  

  Здесь T — тензор напряжений жидкости [7]

  
  

  T = ( — p + A V- v ) E + 2 — e ,            (9)

  
  

  Г dv, Sv_k 2    d v _z)

  +       ^к

  (а Х_к d X i з ^ik d x i ¹

  
  

  Здесь с = A + — и — объемная вязкость.

  
  
  
  

  Отметим, что прежде всего вызывает сомнение справедливость утверждения: " Значение средней силы не зависит от того, где проведена поверхность интегрирования '' ([8, с. 48], первый абзац), повторяющегося во всех работах [7–10], со ссылкой на работы [21–23] (в работе [10] дано уточнение о том, что эта инвариантность справедлива при оценке интеграла (10) с точностью до величин второго порядка малости). О подобном утверждении в работах [21, 22] упоминалось в работе [1], однако в работе [23] такого утверждения для вязкой жидкости нам найти не удалось. Напротив, там есть следующее утверждение (с. 65): " Вязкость (внутреннее трение) жидкости проявляется в наличии еще дополнительного, необратимого

  
  

  переноса импульса из мест с большей в места с меньшей скоростью " . А это говорит о потерях импульса в вязкой среде. Более того, в работе [1] дано косвенное доказательство того факта, что значение интеграла (10) для вязкой жидкости зависит от выбора поверхности S , охватывающей частицу, т. к. в вязкой жидкости происходит потеря импульса вне зависимости от наличия или отсутствия неоднородных включений.

  В целом надо отдать должное циклу работ [7– 10], т. к. в них впервые была осуществлена попытка учета влияния акустического течения на силу радиационного давления в вязкой теплопроводящей жидкости. В указанном цикле работ принимается допущение об аксиальной симметричности первичного поля; включения предполагаются сферическими.

  3. Анализ работ [11–15]. Наиболее полно и одновременно корректно, по мнению автора, выражения для силы радиационного давления в вязкой жидкости рассмотрены в этом цикле работ. Базовые выражения для баротропной жидкости приведены в работе [11], частично — в [12]; для вязкой теплопроводящей жидкости — в работе [14]. Остановимся на базовых соотношениях, приведенных в этих работах. Ограничение накладывается на характер первичного поля — принимается его аксиальная симметрия, а также на форму включения — она принимается сферической.

  За основу берется система, состоящая из закона сохранения импульса в дифференциальной форме и уравнения неразрывности жидкости

  
  

  где S ₀ — равновесная поверхность включения; S ( t ) — временнáя зависимость площади поверхности включения; T _k ⁽¹⁾ , T _k ⁽²⁾ — тензоры напряжений первого и второго порядков малости, определяемые из (*) при подстановке туда значений давления и скорости соответственно первого и второго порядков малости. После стандартных процедур, использующих кинематическую теорему переноса (см. аналогичный вывод в [1]), автор получает с точностью до величин второго порядка малости следующее выражение для СРД:

  
  

  F

  
  

  = J ( r-i”

  S 0

  
  

  ^- P o v ^(V v k'^ n k d s .

  
  
  
  

  Для T _k ⁽¹⁾ и T _k ⁽²⁾ автор получает следующие системы уравнений (для примера приведем только случай баротропной жидкости):

  
  

  d v, °)     d T , ;¹)

  P o^T" =     ,

  d t      d x _k

  др ⁽¹⁾           dv i⁽¹⁾

  d t       P 0 d x, ’

  p ⁽¹⁾ = c ² p ⁽¹⁾;

  
  

  a( p⁽¹⁾v i ⁽¹⁾)

  
  

  d t

  
  

  + ^po

  
  
  
  
  

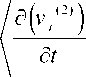
  |:⁽ Р V ) = -   ^(п ' к ) = ^⁽ T - Р v vk ) ,

  о t           о x_k          о x_k

  
  

  др д t

  
  

  _-

  
  

  ^⁽ P V ) . д x i

  
  
  
  

  ρ ₀ v_i (1) v_k (1) ,

  
  

  Здесь T _k — тензор напряжений в вязкой жидкости, определенный в (9), который перепишем в форме, фигурирующей в цитируемых работах:

  
  

  = ^d   IT (2)

  ~ V ik

  5 xk '

  
  
  
  
  

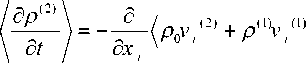
  „ к     Г д vi d vk 2 д V,)

  Tik = -р^л + р д +д т д ^1 +

  ^ dx k   дxi   3 дx,

  д V]

  + £8

  a x ,

  Далее автор ищет СРД по Рэлею

  
  

  (*)

  
  

  Все дальнейшие выкладки в работах [11–15] автор проводит стандартными методами применительно к выбранной модели включения и первичного поля.

  Отметим, что условием инвариантности СРД в (13) с точностью до величин второго порядка малости по отношению к произвольной поверхности интегрирования S , содержащей внутри себя S ₀

  
  
  
  
  

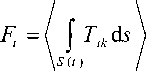
  J T _ь °) n k d s

  S ( t )

  
  
  
  
  
  
  
  

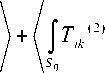
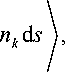
  F, = I" T *²⁾ - p v, ⁽¹v ?’)) n_k d s =

  i            ik          0 i k         k

  S 0

  (2)            (1)    (1)

  J T ik P o ^v i v k   n^l k d ³ ,

  S

  
  
  
  

  является равенство нулю с точностью до величин третьего порядка малости дивергенции подынте-

  
  

• 3)    жидкость является баротропной, т. е. давление p зависит только от плотности ρ

Р = f ( Р ) ;                   ⁽¹⁾

• 4)    падающее поле полагается безвихревым;

• 5)    предполагается, что жидкость удовлетворяет условию Стокса

Л +— ц — 0, что означает равенство нулю объемной (второй) вязкости ς

^ — Л + 3 ц — 0;              (2)

здесь λ , µ — параметры Ламе (коэффициенты динамической вязкости) жидкости, µ носит еще название коэффициента сдвиговой вязкости.

Отметим сразу, что вклад тепловых эффектов может быть соизмерим с вкладом вязкости (см., например, [7]). Соотношение же (2) с достаточной степенью точности выполняется для одноатомных газов, а ([16, с. 209]) " для многоатомных газов и жидкостей коэффициент Л >  0 может иногда во много раз превосходить по величине коэффициент ц " , который также положителен [17, с. 79].

Остановимся на способе решения заявленной в работах [2–6] задачи, которая сводится к рассмот- рению линеаризованной системы уравнений Навье—Стокса [18]:

—— ^— A v + — V p — ^{1 —} V ( V- v ) = 0, a t P o       P o      3 P o

—— + V- v = 0,

P o 5 1

d p = c 2 dp ⁰

Здесь ρ ₀ , c ₀ — плотность и скорость звука в жидкости в состоянии покоя; v — колебательная скорость частиц жидкости. Решение задачи (3) ищется с помощью введения скалярного и векторного потенциалов [18]

v = —( VФ + Vx T ) , V- T = 0, a t^{v            h}                       (4)

• ^v = ( v 1 , v 2 , v 3 ) ,

где скалярный Ф и векторный T потенциалы определяются уравнениями

L 4 1 ^д) 1 + и

(     3 c ₀ ² a t )

1 а ² c ₀ ² a t²

^Ф = 0,        (5)

A

где E — единичная матрица, а e — тензор скоростей деформаций, который равен e = ij

1 Гд v, d v, )

*- + ^J- .

2 l a x, d x, ji

В случае идеальной жидкости A , — ^ 0 выражение (8) переходит в соответствующее выражение для идеальной жидкости [19].

Как уже отмечалось выше, авторами рассматривался только случай жесткой частицы. Что касается жидких или упругих частиц, то для этого случая при осреднении выражения (8) необходимо усреднять и граничную поверхность частицы, которая будет функцией времени S = S ( t ), что приведет к другому выражению для радиационного давления (см., например, [1, 20]).

Кроме того, в описанном подходе не учитывается вклад акустического течения в силу радиационного давления на частицу.

грального выражения в (13), (17) во всем объеме жидкости, ограниченном поверхностями S и S ₀ (что следует из теоремы Гаусса), а именно

T ik / xk

= P o — Vv.1S ⁽¹⁾) + O ( P ⁽³⁾, v ⁽³⁾, P ⁽³⁾).       (18)

xk

Как видно из сравнения (15) и (18), выражение (17) справедливо при условии

I d( P V )\   М/²⁾ )\

+ P0

\    dt\ d

= O(p^\v(3),p(3)).

Здесь под O ( p ⁽³⁾, v ⁽³⁾, ρ ⁽³⁾) понимаются величины третьего порядка малости.

В работах [11, 12] автор приводит некоторые правдоподобные рассуждения об условиях, при которых уравнение (15) сводится к уравнению (19), позволяя тем самым получить инвариантность СРД от поверхности интегрирования. В работе [14] для случая вязкой теплопроводящей жидкости автор вообще уходит от обсуждения этого вопроса ввиду его большей сложности. Поэтому, как нам представляется, этот вопрос требует самостоятельной проработки.

ВЫВОДЫ

Таким образом, проведен качественный обзор публикаций, относящихся к расчету радиационного давления в вязких, теплопроводящих жидкостях. Из всей массы работ по этой тематике выбраны три наиболее полных цикла публикаций. Приведены принятые в этих работах соответствующие базовые выражения, позволяющие рассчитать силы радиационного давления, а также принятые при этом допущения и ограничения. Показано, что в случае вязкой жидкости необходимо дополнительно обосновывать инвариантность выбора границы интегрирования в методе расчета радиационных сил.