Анализ работы напорного пневмоклапана пневмогидравлического амортизатора пониженной ударовибропроводимости

Амортизирующие устройства, применяемые для гашения ударов при посадке и транспортировке в условиях стеснённых компоновок различных агрегатов ракетно-космической техники, должны обеспечивать непревышение допускаемых перегрузок при заданных ограничениях на ходах, быстрое затухание колебаний и возврат амортизируемого объекта в исходное положение, а также обладать высоким значением энергоёмкости. Максимальная работа амортизатора на заданном ходе обеспечивается при движении защищаемого объекта с максимально до-

пустимой перегрузкой [1], т.е. при характеристике, близкой к релейной. При этом необходимо избегать быстрого возрастания усилия амортизатора, так как это может вызвать интенсивные собственные колебания амортизируемого объекта. Рассматривается амортизируемая система, в которой при кинематическом воздействии на ускорение основания как твердого тела может накладываться интенсивная вибрация, что существенно ограничивает применение традиционных типов амортизаторов, в частности гидродемпферов [2–4].

Для достижения характеристики, близкой к релейной, разработаны различные типы амортизирующих устройств: эластомерные (арочные, сотовые) амортизаторы с потерей устойчивости [5, 6], а также различные типы амортизаторов, элементы которых

If I— 0СМ1ЛМЕ АППАРАТЫ VI

ТЕХНОЛОГА иен

работают в условиях предварительного поджатия к упору и включаются в работу при превышении определённого усилия [7].

В БГТУ «ВОЕНМЕХ» им. Д. Ф. Устинова была предложена оригинальная схема пневмогидравлических амортизаторов (ПГА) пониженной ударо-вибропроводимости, которая достигается за счет использования нормально открытых клапанов или закрытых клапанов с малой жесткостью поджатия [8]. Давление жидкости в рабочей камере (далее РК) создаётся за счет сжатия газа в пневматических полостях – аккумуляторах давления. В ПГА может быть несколько аккумуляторов давления – один основной (ОАД) и один-два дополнительных (ДАД) [8, 9]. ОАД работает на всём диапазоне давлений жидкости и перемещений поршня, как при сжатии амортизатора, так и при отбое. ДАД включаются в работу в определённом диапазоне давлений и служат для скачкообразного уменьшения жёсткости силовых характеристик амортизатора, т.е. для приближения статической характеристики к релейной.

Целью работы является исследование работоспособности схемы ПГА с напорным пневмокла- паном и влияния параметров напорного пневмоклапана ОАД на движение амортизируемого груза. Результаты расчётов, полученные в данной статье, также позволят проверить применимость более простых математических моделей ПГА, в которых не учитывается инерция клапанов и сжимаемость жидкости.

Работе ПГА с ДАД посвящено исследование [9]. Так как в настоящей статье исследуется работа напорного клапана ОАД, основной функцией которого является окончательное гашение колебаний, происходящих без включения в работу ДАД, то для

Том 8

упрощения математической модели рассматривается ПГА без ДАД.

1.    Общие положения

Схема ПГА с обозначением основных его частей показана на рисунке 1. Газовая полость напорного клапана 7 соединена с газовой полостью основного аккумулятора давления 3 через дроссель малого сечения 9 и обратный клапан 8.

Напорный клапан 7 и обратный клапан 5 за счёт пружины сжатия с малым поджатием нормально закрыты. Гибкая разделительная мембрана 4 поддерживает равенство давлений газа и жидкости в ОАД 3. Таким образом, в равновесном состоянии давления во всех объемах системы равны.

Рассмотрим случай, когда воздействие начинается со сжатия ПГА. Движение поршня (его перемещение на рисунке 1 обозначено как s ) вызывает повышение давления жидкости в РК 1. Клапан 11, который на этом этапе прижат к седлу только усилием поджатия пружины, открывается, и жидкость из РК 1, проходя через клапанный зазор, попадает в ОАД 3, сжимая газ в газовой полости. Повышенное давление газа действует на обратный клапан 8, открывая его, и через клапанный зазор газ поступает в полость 12, повышая давление в ней.

После того как поршень 2 начинает двигать в сторону отбоя, давление жидкости в РК 1 начинает падать и становится ниже давления в ОАД 3. Это приводит к закрытию напорного клапана 11 и открытию обратного клапана 5. Через открывшийся обратный клапан 5 и дроссель 6 жидкость из ОАД начинает перетекать в РК. Давление газа в ОАД 3

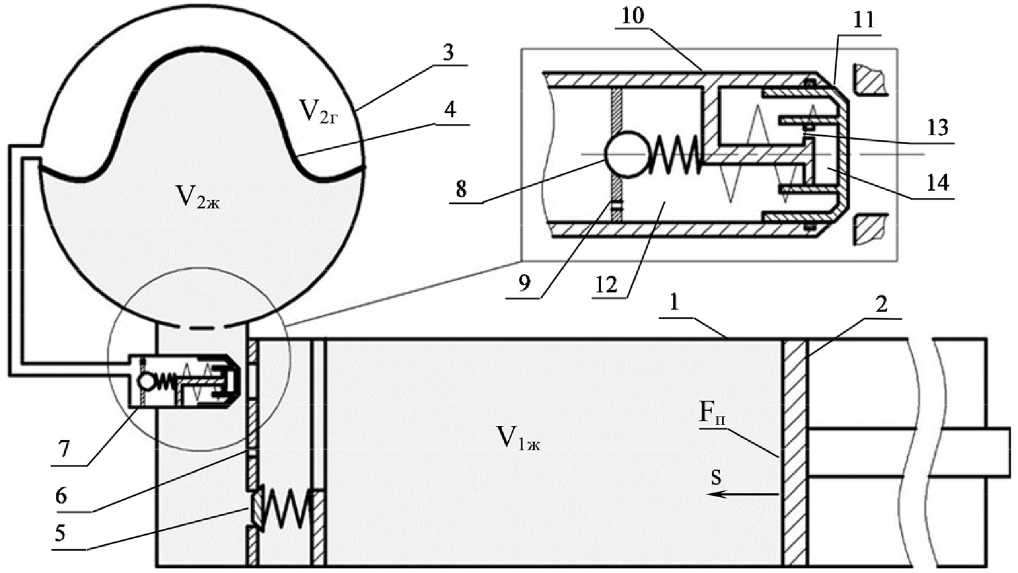
Рисунок 1. Схема ПГА: 1 – РК; 2 – шток с поршнем; 3 – ОАД; 4 – разделительная мембрана ОАД;

5 – обратный клапан ОАД; 6 – дроссель ОАД; 7 – напорный клапан; 8 – обратный клапан напорного клапана; 9 – дроссель малого сечения; 10 – неподвижный корпус напорного клапана;

11 – подвижная тарель напорного клапана; 12 – газовая полость; 13 – дроссель демпферной полости;

14 – демпферная полость

начинает падать и сравнивается с давлением газа в камере 12, после чего обратный клапан 8 закрывается. Так как площадь сечения дросселя 9 мала, то давление в полости 12 остаётся высоким и существенно превышает давление жидкости в РК 1.

После остановки поршня (в растянутом состоянии амортизатора) начинается новый цикл колебаний – амортизатор сжимается. Обратный клапан 5 закрывается. Для быстрого гашения колебаний за счёт перепада давления на дросселе 6 напорный клапан 7 должен оставаться закрытым до тех пор, пока давление существенно не превысит начальное. Также к концу колебаний давление газа в полости 12 напорного клапана должно понизиться до начального для готовности к последующему воздействию. Для достижения такого режима работы амортизатора дроссель 9 и газовая полость 12 напорного клапана должны иметь соответствующие размеры.

2.    Математическая модель

В настоящей работе рассматривается одномассовая модель груза (амортизированного объекта), установленного на амортизаторе, имеющего одну степень свободы и рассматривающегося как точечная масса. Расчётная схема показана на рисунке 2а. Амортизатор жёстко закреплён на подвижном основании в вертикальном положении. Суммарную массу груза вместе со штоком и поршнем обозначим через m. Направление движения основания sy0, груза sy и направление действия ускорения свободного падения показаны на рисунке 2.

Для описания параметров жидкости и газа используется нульмерный подход: области, занимаемые жидкостью и газом, разбиваются на объемы, в пределах каждого из которых параметры жидкости (газа) в каждый момент времени считаются постоянными по объему. Выделяем два гидравлических объема (РК 1 и гидравлическая

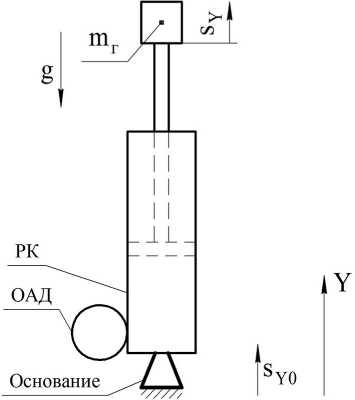
Рисунок 2. Расчётная схема: схема воздействия полость ОАД 3) и три газовых (газовая полость ОАД 3, газовая полость напорного клапана 12 и демпферная полость 14). Для расчета перетекания жидкости и газа из объема в объем будем использовать соотношения для установившегося истечения через малое отверстие. Считаем, что и масса разделительной мембраны 4 мала в сравнении с массой жидкости, и, таким образом, давления газа и жидкости в ОАД 3 в каждый момент одинаковы. Принимаем, что трение между поршнем и корпусом ПГА отсутствует. Пренебрегаем трением и теплообменом жидкости и газа со стенками. Пренебрегаем инерцией обратных клапа-   73

нов 5 и 8, считая, что в зависимости от перепада давления каждый из них либо закрыт, либо открыт на максимальное проходное сечение. При расчете гидродинамической силы, действующей на напорный клапан, считаем, что в каждый момент времени имеет место квазистационарное истечение жидкости через зазор и угол истечения постоянен. Для упрощения математической модели принимается, что плотность жидкости ρ постоянна, сжимаемость жидкости учитывается через дифференциальную зависимость давления от объема. Погрешность, вносимая данным упрощением, является приемлемой для инженерных расчётов.

Также не учитываются поршневой эффект [10] в гидравлических полостях, связанный с изменением объемов камер при перемещениях тарелей клапанов, податливость стенок (за исключением разделительной мембраны) и наличие нераство-рённого воздуха .

В начальный момент времени груз находится в положении статического равновесия – вес груза уравновешен статической реакцией амортизатора. Амортизатор имеет равные хода вверх и вниз из положения статического равновесия. Моделирование движения груза с учётом работы ПГА производится в программном модуле Matlab Simulink 2017b.

Сжатие амортизатора (смещение поршня относительно корпуса) будем обозначать через s (в положении равновесия s=0; при расширении s<0). Имеем s = sy0 - Sy .                       (1)

Ускорение груза a определяется выражением a = s = Fn • (P1 - Ратм )/m - g,          (2)

где FП – площадь поршня; m – масса груза; р1 – давление жидкости в РК; ратм – атмосферное давление.

Уравнение изменения давления р1 в РК 1 определяется по формуле [11]

• _¹ F n • s - q i ^p i =-- 77-----,

1ж

где q 1 - объёмный расход из РК; в — коэффициент объёмного сжатия жидкости; V_1ж - объём жидкости в РК.

Объёмный расход из РК в ОАД в общем случае определяется выражением qi = q др+q нк+q ок,                 (4)

где q_др – объёмный расход через дроссель; q_нк – объёмный расход че р ез напорный клапан; q_ок – объёмный расход через обратный клапан.

Обозначим через Др12 перепад давления жидкости между РК и ОАД,

А Р 12 = P i — Р 2 ,                    ⁽⁵⁾

где р2 – давление жидкости в ОАД. Знак перепада давления Др12 определяет направление течения жидкости в каждом сопротивлении, а также положение обратного клапана. Площадь проходного сечения Аок обратного клапана определяется выражением

Аок =10, ЛР12 > 0       , ок   ((Аок)тах, АР12 < 0

где (А о _к)_тах — максимальная площадь проходного сечения полностью открытого обратного клапана ОАД.

Объёмный расход в ОАД из РК определяется конфигурацией и размером проходного сечения каждого сопротивления, а также перепадом давления на сопротивлении. Величина объёмного расхода qc через отдельное сопротивление выражается формулой [12]

q с = ^c_c(Re) • A c •

² •^{А Р12} ρ

где C_c(Re) - коэффициент расхода через сопротивление, зависящий от числа Р ейнольдса;

A_c - площадь проходного сечения сопротивления; ρ – плотность рабочей ж и дкости.

Полный объём ОАД – постоянный и равен сумме объёма жидкости и газа. Величины приращения объёма жидкости и газа в ОАД равны по модулю, но противоположны по знаку, так как увеличение объёма жидкости вызывает уменьшение объёма газа dV. =-dVir.                  (8)

Сжимаемость газа существенно выше, чем у жидкости. Инерцией разделительной мембраны пренебрегаем. В связи с этим в аккумуляторе давления жидкость считаем несжимаемой, а её давление принимаем равным давлению газа

Р 2 = Р 2 г -                           (⁹)

Схема напорного клапана показана на рисун-3

. Реакцию, действующую со стороны жидкости на тарель клапана, условно разделим на статическую и гидродинамическую составляющие.

Площадь проходного сечени я А_нк напорног о клапана определяется выражением

^А„= ^п^ .,h.. .             (Ю)

где d_нк – диаметр отверстия в седле напорного клапана; h_нк – высота подъёма тарели напорного клапана. Максимальная выс от а п одъёма та рели напорного клапана ограничена значением, р а вным 0,25∙d нк , согласно [13].

Статическая составляющая реакции Rст от давлений жидкости и газа, действующих на тарель напорного клапана, определяется выражением

R ст = Р 1 • F .K - Р 4г • F ._K1 - Р 5г • F .K2 ,        00

где Fнк, Fнк1 и Fнк2 – площади участков тарели напорного клапана, на которые действуют давле-

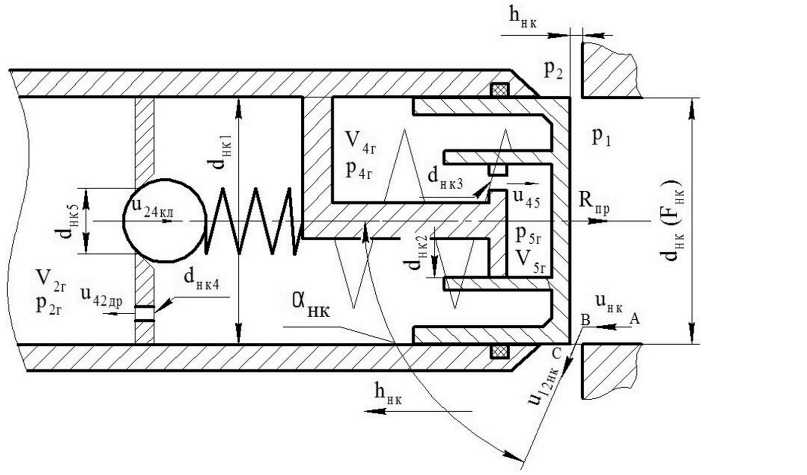
Рисунок 3. Схема напорного пневмоклапана

ние жидкости р 1 , давления в газовой р_4г и демпферной р_5г полостях со о тветстве нно.

Гидродинамическая сила Rrg, действующая на тарель напорного клапана, определяется из уравнения количества движения для контура АВС (см. рисунок 3)

G„ - и„ - pi, г-А. - С,, J J J J J

^R гд = q нк ^-р^-

q нк

—

q нк

I FHK   AHк- sinaHK нк       нк        нк

- cos а_нк нк

,

где α_нк – угол истечения жидкости из кольцевого зазора, отсчитанный от оси клапана. В литературе [14] для клапан о в с плоско й поверхностью тарели и острыми кромками принимают значение угла α_нк равным 69°.

Усилие пружины напорного клапана определяется по формуле

где A ij - площадь проходного сечения сопротивления между полостью с индексом «i» и полостью с индексом «j», C_ij – коэффициент расхода.

В соответствии с допущением обратный клапан 8 (см. рисунок 1) либо полностью открыт, либо закрыт. Положение обратного клапана 8 определяется знаком пер еп ада д авления ∆ р 24г . Площадь проходного сечения А_24кл обратного клапана 8 определяется выражением

А        __

А 24кл ^—

0, V 0    ,

,^(А 24кл ) тах , ^ ^р 24г >  ⁰

R пр = ^kпр • (Х 0 + ^h_Hк ),               (13)

где х₀ – началь н ое поджа ти е п р уж и ны; k_пр – жёсткость пружины.

Далее рассмотрим зависимости для определения параметров г аза в амор тизато ре. Плотность газа p_ir в газовых полостях определяется по формуле

P ir = m ,г /V,

где V_iг – объём газа в газовых полостя х с учётом его изменения при перемещении клапанов и мембраны; m iг – масса газа в газовых полостях.

Далее рассмотрим истечение газа между полостями через зазор или дроссел ирующ ее отверстие. Для определённости примем, что в полости с индексом «i» деление выше, чем в полости с индексом «j».

Критическое давление газа при перетекании через отверстие малого сечения определяется по формуле р-р-р..(2/(к+1))'““—■», (15)

где (А 24кл ) тах — максимальная площадь проходного сечения обратного клапана 8, Δp₂₄=p₂-p₄, p₄ – давление в полости 12 напорного пневмоклапана.

Далее рассмотрим дифференциальные уравнения для газовых полостей (объемов). Для определенности примем, что i – н о м е р полости, для которой записываются уравнения, k - номер полости, в которой давление газа вы ше , ч ем в по л ости с индексом i и из которой га з по с тупа е т в полость i, а j – номер полости, в к от орой д авл ение газа ниже, чем в полости с индексом i, и в которую газ поступает из полости i. Измен е ние энергии в i-й газовой полости в общем случае определяется выражением

ET = ^Gki - c p - Тг — ^Gij - C p - ^Т.г + Р ,г - V, (21)

где ср - теплоемкость газа при постоянном давлении; Vir - скорость изменения объёма газа в рассматриваемой i-й полости.

Давление р^ температура Т_iг и изменение массы газа m _i в i-й газовой полости определяются выражениям и

pi

_ E_ir - (к — 1)

где k – показатель адиабаты газа.

Давление в отверстии р^_г зависит от режима истечения газа и равн яется максимальному из двух [15, 16]: давлению в полости за отверстием р_jг (докритический режим) или к р итическому давлению р_кр (крит ически й режи м)

где ёме.

Т iг

;

iг

E iг     _;

^т .г ^{- C} V

^т.г - ^Gki ^{— G}ij ,

су - теплоемкость газа при постоянном объ-

P ij _г = max( р^рД            (16)

Плотность ρijг, скорость uij и расход Gij газа при перетекании через отверстие малого сечения определяются по формулам

P ij г = p. - (Р .К /р .г )^(I/k);                (17)

Уравнение движения напорного клапана имеет

вид

h нк ^{- (R} гд ^{+ R} ст ^{+ R} пр

h

— ГО ^R - )/m нк ■ h нк

u j =

2 - к Р ir --- к — I P ir

1 —

V

p ijг

к - 1 Л ^k

P ir J

;

где mнк – масса напорного клапана; Rтр – сила трения в уплотнении клапана.

Сила трения уплотнительного кольца круглого сечения зависит от величины сжатия кольца и давления жидкости, а величина каждой составляющей силы трения определяется по графикам, при-

ведённым в [17]. Анализируя указанные графики для упрощения математической модели, силу трения R_тр в уплотнении клапана можн о вы разить формулой

R тр = k • п • d нк ,                  (26)

где k - коэффициент, учитывающий деформацию поджатия уплотнительных колец, твердость резины и начальное давление в амортизаторе. Можно принять k1=500 Н/м.

При численном моделировании динамики напорного клапана учитывались его отскоки от седла ⁷⁶ и верхнего упора при полном закрытии и полном открытии. Считалось, что в результате соударения скорость клапана изменялась на противоположную, а ее модуль составлял к_в (коэффициент восстановления) от модуля скорости до соударения. Коэффициент восстановления принимался равным k_в=0,56.

3.    Результаты расчётов

В настоящем разделе представлены результаты расчётов параметров движения груза на амортизаторе перемещения напорного клапана. Параметры ПГА, рабочей жидкости и газа, принимаемые в расчётах, приведены в таблице 1.

График зависимости кинематического воздействия (перемещения) основания от времени показан на рисунке 4. Рассматриваются два воздействия: полное с перемещением основания smax и половинчатое с амплитудой 0,5∙smax.

Временные зависимости перемещения груза относительно основания (штока относительно корпуса ПГА) при различных диаметрах дросселя 9 dнк4 и объёмах газовой полости 12 V40 показаны

№ 2 (48) 2024 Том 8

на рисунке 5, зависимости перемещения тарели напорного клапана – на рисунке 6.

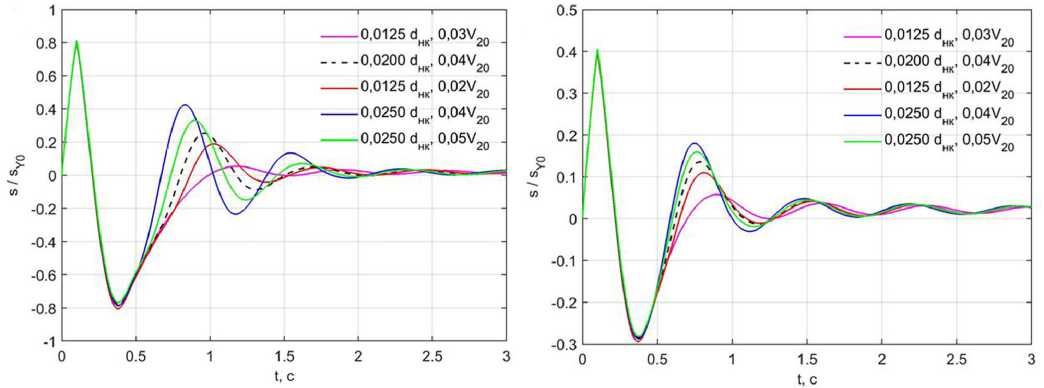
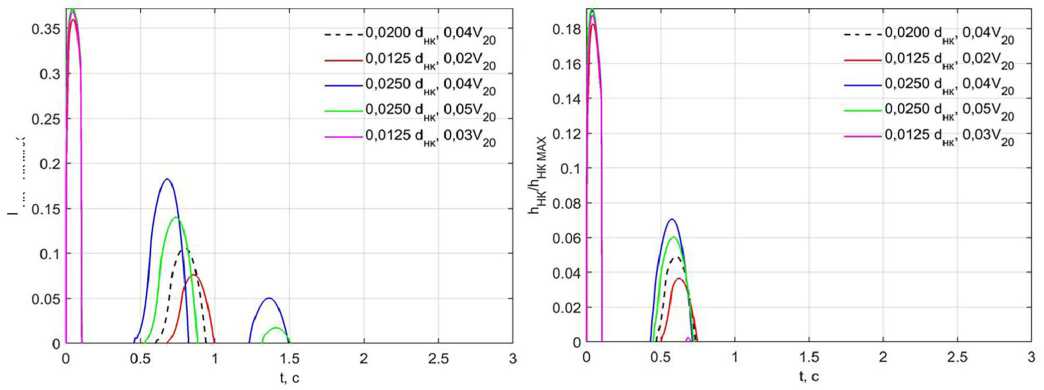
Чем меньше дроссель 9 при фиксированном объёме газовой полости 12 напорного клапана 7, тем дольше последний остаётся закрытым после воздействия. При фиксированном диаметре дросселя 9 напорный клапан 7 тем дольше остаётся закрытым, чем больше объём газовой полости 12.

Как показывают расчёты, при рассматриваемых сочетаниях параметров для эффективного гашения колебаний дроссель 9 должен иметь диаметр dнк4=0,0125–0,02dнк при объёме газовой полости 12 напорного клапана V40=0.02–0,03V20. При большем диаметре дросселя 9 напорный клапан 7 открывается при каждом повышении давления в РК 1. Колебания амортизируемого объекта при этом затухают дольше. При меньшем диаметре дросселя 9 часть газа, притёкшая из АД 3 в напорный клапан 7, запирается в газовой полости 12. В результате этого после затухания колебаний происходит медленный возврат амортизатором груза в исходное положение (из-за медленного истечения газа обратно из напорного клапана в ОАД). Большой объём газовой полости 12 также может привести к длительному запиранию там части газа из АД 3, а также влечёт за собой увеличенные габариты конструкции.

Таким образом, работа напорного клапана способствует значительному усилению гашения колебаний амортизируемого объекта при малых габаритных размерах в конструкции ПГА. Расчёты показывают, что напорный клапан способствует гашению колебаний как при воздействии с максимально допустимым перемещением основания, так и при воздействии меньшей интенсивности.

Таблица 1

Параметр	Значение
Диаметр обратного клапана, dок	0,2d п
Диаметр напорного клапана, dнк	0,2d п
Диаметр дросселя 6, dдр	0,05d п
Объём газа в ОАД в равновесном положении, V20г	3∙Fп∙smax
Диаметр тарели напорного клапана 11, dнк1	dнк
Диаметр демпферной камеры 14, dнк2	0,5d нк
Диаметр дросселя 13, dнк3	0,025d нк
Начальный объём демпферной полости 14, V50	0,002V 20г
Коэффициент расхода через дроссель Cдр	0,62
Коэффициент расхода через клапан Снк	0,75
Плотность рабочей жидкости ρ, кг/м3	830
Коэффициент объёмного сжатия β, Па-1	7∙10–10
Коэффициент кинематической вязкости ν, м2/с	2,1∙10–5
Показатель адиабаты газа, k	1,4

Параметры ПГА и рабочих тел

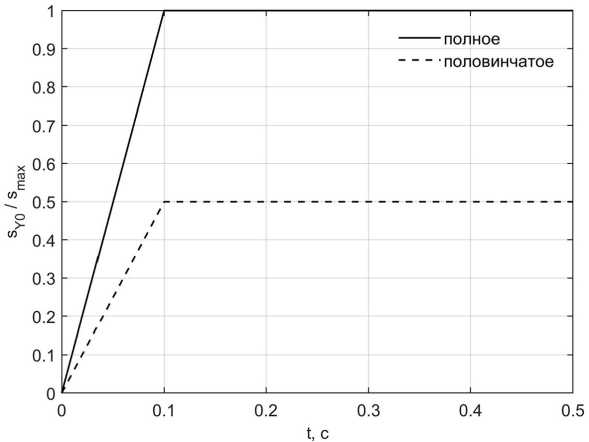
Рисунок 4. График перемещения основания

а)                                                                б)

Рисунок 5. Относительное перемещение груза при различных dнк4 и V40 при воздействии: а – полном; б – половинчатом

^К^НКМАХ

а)                                                                б)

Рисунок 6. Перемещение тарели напорного клапана при различных dнк4 и V40 при воздействии: а – полном; б – половинчатом

I— ОСМИЧЕСКИЕ АППАРАТЫ VI ТЕХНОЛОГИИ ws

Заключение

Предложена математическая модель динамики пневмогидравлического амортизатора. По результатам серии тестовых расчётов отдельного пневмогидравлического амортизатора установлены относительные характерные размеры напорного клапана, обеспечивающие, с одной стороны, демпфирование колебаний, с другой – быстрый возврат амортизируемого объекта в исходное положение статического равновесия. Результаты расчётов

Том 8

показывают, что для этого диаметр дросселя напорного клапана должен быть в диапазоне от 1,25 до 2 % от диаметра тарели напорного клапана при значениях ёмкости газовой полости напорного клапана от 2 до 3 % от объёма газа в аккумуляторе давления в равновесном положении.

Расчёты показали работоспособность схемы пневмогидравлического амортизатора, предложенной в БГТУ «ВОЕНМЕХ». При этом напорный клапан практически не увеличивает габариты амортизатора.