Анализ расчетных моделей при расчете прочности наклонных сечений железобетонных балок на действие поперечных сил
Автор: Филатов Валерий Борисович, Арцыбасов Антон Сергеевич, Багаутдинов Марсель Азатович, Гордеев Дмитрий Игорьевич, Кортунов Александригоревич, Никитин Роман Анатольевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Современные наукоемкие инновационные технологии
Статья в выпуске: 4-3 т.16, 2014 года.
Бесплатный доступ
Рассмотрены расчетные модели для определения прочности наклонных сечений изгибаемых железобетонных элементов без поперечной арматуры на действие поперечной силы, принятые в нормативных документах и предложенные в их развитие. Приведен пример оценки прочности наклонных сечений железобетонной балки в зависимости от процента продольного армирования по некоторым расчетным моделям. Показано, что учет продольного армирования при расчете прочности железобетонных балок на действие поперечных сил позволяет повысить конструктивную надежность и безопасность проектных решений, в том числе для элементов из высокопрочного бетона.
Изгибаемый железобетонный элемент, наклонное сечение, расчетная модель, поперечная сила, высокопрочный бетон
Короткий адрес: https://sciup.org/148203269
IDR: 148203269 | УДК: 624.012.45.046
Текст научной статьи Анализ расчетных моделей при расчете прочности наклонных сечений железобетонных балок на действие поперечных сил
Разработка и внедрение прогрессивных строительных технологий и конструкций, в том числе на основе высокопрочных материалов, требуют опережающего развития нормативнотехнической базы строительства, совершенствования существующих и разработки новых методов в области расчета и проектирования конструкций. Такое развитие возможно на основе обширных экспериментально-теоретических исследований, направленных на обеспечение конструктивной надежности и эксплуатационной безопасности возводимых зданий и сооружений. Одним из важнейших факторов, определяющих эксплуатационную безопасность конструкции, является соответствие принятой расчетной модели действительному характеру работы рассматриваемого сечения и всей конструкции в целом.
Расчетная модель для определения прочности наклонных сечений железобетонной балки при действии поперечных сил имеет эмпирический характер, обусловленный сложностью напряженно-деформированного состояния композитного материала (каковым, по сути, является железобетон) в зоне поперечного изгиба.
Арцыбасов Антон Сергеевич, студент Багаутдинов Марсель Азатович, студент Гордеев Дмитрий Игорьевич, студент Кортунов АлександрИгоревич, студент Никитин Роман Анатольевич, студент
Прочность наклонных сечений изгибаемых элементов в действующих нормах по расчету железобетонных конструкций [1] рассчитывают из условия, что усилия от внешних нагрузок, действующие в наклонном сечении, не должны превышать внутренних предельных усилий в этом сечении. Для балки без поперечного армирования внутренним расчетным усилием, определяющим несущую способность элемента при действии поперечных сил в соответствии с принятой в [1] расчетной моделью, является касательное усилие в сжатой зоне бетона Qb. Эмпирическая зависимость для определения Qb, как функция от прочности бетона на сжатие и длины проекции наклонной трещины, изначально была предложена М.С. Боришан-ским по результатам экспериментальных исследований на балках без поперечного армирования из бетона средней прочности [2]. Впоследствии было установлено, что несущая способность наклонных сечений при действии поперечных сил не возрастает прямо пропорционально прочности бетона на сжатие, а изменяется по параболической кривой, вследствие чего прочность бетона на сжатие была заменена на прочность бетона при растяжении. В дальнейшем экспериментальные исследования [3] показали, что в наклонном сечении действуют усилия, в явном виде неучтенные в расчетной модели: касательное усилие в продольной растянутой арматуре (нагельный эффект) и силы зацепления по берегам наклонной трещины. Метод расчета прочности железобетонных элементов по наклонным сечениям с учетом усилия нагельного эффекта и сил зацепления по берегам наклонной трещины был предложен А.С. Залесовым [4]. Однако, из-за недостаточности опытных данных, в нормативной методике расчета эти усилия продолжали учитывать косвенно – через величину Qb [5].
Методика расчета прочности наклонных сечений, учитывающая усилие нагельного эффекта и силы зацепления в наклонной трещине была предложена авторами [6-8]. Расчетные зависимости включают в себя следующие усилия: суммарное усилие в хомутах, пересекающих наклонную трещину, касательное усилие, возникающее в продольной растянутой арматуре; касательные усилия сопротивления сдвигу берегов наклонной трещины. Касательное усилие в сжатой зоне бетона определяется по уточненной зависимости [6], позволяющей избежать дополнительных ограничений эмпирического характера, но в условии прочности касательное усилие Q b выражается через остальные компоненты напряженного состояния. Касательные усилия сопротивления сдвигу берегов наклонной трещины по предложению [7, 8] зависят от прочности бетона на растяжение и угла наклона трещины.
Анализ результатов экспериментальных исследований прочности наклонных сечений изгибаемых железобетонных элементов [9, 10] показывает, что прочность изгибаемых элементов действию перерезывающих сил также зависит от процента армирования сечения продольной арматурой и высоты сечения элемента (так называемый «масштабный эффект»). Влияние процента продольного армирования балок на их сопротивление поперечному изгибу отмечалось и ранее [5], однако эмпирический характер расчетных зависимостей не позволял выделить и проанализировать влияние этого фактора.
Нормативные методики расчета прочности изгибаемых элементов на действие поперечных сил, принятые за рубежом [11, 12] также являются эмпирическими. По структуре расчетных зависимостей наиболее близкими являются отечественные [1] и американские [11] нормы, в которых касательное усилие в сжатой зоне бетона определяется только его прочностью. В европейских нормах [12] касательное усилие в сжатой зоне бетона также зависит от величины процента продольного армирования и высоты сечения изгибаемого элемента, влияние которых учитывается введением в расчетные зависимости эмпирических коэффициентов. Осознавая ограниченность эмпирического подхода для дальнейшего развития теории прочности железобетонных элементов при действии поперечных сил, предпринимаются попытки определения прочности на основе полуэмпирического подхода, одним из примеров которого является модифицированная теория полей сжатия (MCFT), предложенная авторами [13] и успешно конкурирующая с нормативным методом расчета прочности железобетонных элементов при действии поперечных сил [11]. Предложенная в [13] методика расчета позволяет, в частности, учитывать процент продольного армирования балки при определении величины касательного усилия в сжатой зоне бетона.
Авторами [14] предложена расчетная модель наклонного сечения изгибаемого железобетонного элемента без поперечной арматуры (рис. 1). Особенностью расчетной модели является выделение в расчетных зависимостях сил зацепления в наклонной трещине как отдельной компоненты в совокупности усилий, обеспечивающих прочность наклонного сечения при расчете на действие поперечной силы. Схема усилий, действующих в наклонном сечении железобетонного элемента, принята в соответствии с [3].
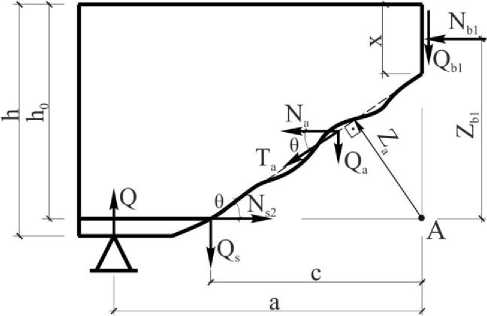
Рис. 1. Расчетная модель наклонного сечения
Предложенная модель позволяет из рассмотрения условий равновесия блока над наклонной трещиной получить компоненты, входящие в условие прочности наклонного сечения изгибаемого элемента на действие поперечной силы:
Q ≤ Q b1 + Q s + Q a , (1)
где Q b1 – касательное усилие в бетоне сжатой зоны в конце наклонной трещины, Q s – касательное усилие в продольной растянутой арматуре в начале наклонной трещины (нагельный эффект), Q a – вертикальная составляющая усилия зацепления по длине наклонной трещины.
Сопоставление результатов расчета прочности наклонных сечений железобетонных балок без поперечной арматуры по нормативным методикам [1, 11, 12] и расчетной модели, предлагаемой в [14] при величине пролета среза a/h0=3, приведено на рис. 2. Анализ графиков показывает, что результаты расчета по зависимостям [14] корреспондируются с результатами расчета по европейским нормам [12]. Наибольшее соответствие результатов наблюдается при величине h0=300 мм, однако с увеличением процента продольного армирования сечения становится заметным превышение расчетных значений по методике [12]. Расхождение между результатами расчета по зависимостям [14] и методике [12] также возрастает с увеличением высоты сечения элемента. Результаты расчета по методикам [1] и [12] корреспондируются при h0=150 мм и проценте продольного армирования не менее 1,5, а также при h0=300 мм и проценте продольного армирования не менее 2. Во всех остальных случаях результаты расчета по методике [1] существенно выше. Та же тенденция характерна и для норм США [11], однако в целом минимальный уровень расчетных значений прочности составляет порядка 75% от значений норм [1].
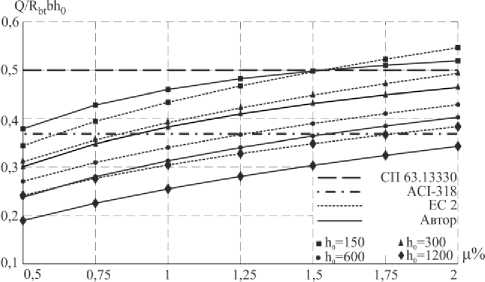
Рис. 2. Сопоставление результатов расчета прочности наклонных сечений
Анализ позволяет сделать вывод о недостаточном соответствии теоретических предпосылок, заложенных в расчетных моделях и фактическом характере работы наклонных сечений изгибаемых железобетонных элементов. Недостаточное соответствие обусловлено эмпирической природой расчетных зависимостей норм [1, 11, 12] при определении прочности наклонных сечений. В свою очередь, эмпирический характер расчетных зависимостей является закономерным следствием значительных трудностей, возникающих при теоретическом исследовании анизотропного материала с нарушенной сплошностью (железобетона) при плоском напряженном состоянии.
Список литературы Анализ расчетных моделей при расчете прочности наклонных сечений железобетонных балок на действие поперечных сил
- Бетонные и железобетонные конструкции. Основные положения: СП 63.13330.2012: утв. Министерством рег. развития Рос. Федерации 29.12.11: ввод в действие с 01.01.13. -М.: ФАУ «ФЦС», 2012. 165 с.
- Боришанский, М.С. Расчет железобетонных элементов при действии поперечных сил//Расчет и конструирование элементов железобетонных конструкций. Сб. тр. НИИЖБ. -М., 1964. С. 122-143.
- Гвоздев, А.А. Силы зацепления в наклонных трещинах/А.А. Гвоздев, А.С. Залесов, И.А. Титов//Бетон и железобетон. 1975. № 7. С. 44-45.
- Залесов, А.С. Новый метод расчета прочности железобетонных элементов по наклонным сечениям//Расчет и конструирование железобетонных конструкций. Сб. тр. НИИЖБ. Вып. 39. -М., 1977. С. 16-28.
- Гвоздев, А.А. Новое в проектировании бетонных и железобетонных конструкций./А.А. Гвоздев, С.А. Дмитриев, Ю.П. Гуща и др. -М.: Стройиздат, 1978. 204 с.
- Карпенко, С.Н. Построение критериев прочности железобетонных конструкций по наклонным трещинам разрушения//ACADEMIA. Архитектура и строительство. 2006. № 2. С. 54-59.
- Карпенко, Н.И. О новом построении критериев прочности железобетонных элементов при действии поперечных сил/Н.И. Карпенко, С.Н. Карпенко//ACADEMIA. Архитектура и строительство. 2006. № 3. С. 26-31.
- Карпенко, С.Н. Об общем подходе к построению теории прочности железобетонных элементов при действии поперечных сил//Бетон и железобетон. 2007. № 2. С. 21-27.
- Collins, M.P. How Safe Are Our Large, Lightly Reinforced Concrete Beams, Slabs and Footings?/M.P. Collins, D. Kuchma//ACI Structural Journal. 1999. Vol. 96, № 4. P. 482-490.
- Филатов, В.Б. Особенности работы и эффективное использование жесткой поперечной арматуры железобетонных балок/В.Б. Филатов, Ю.В. Жильцов//Известия Самарского научного центра РАН. 2012. Т. 14, № 4(5). С. 1325-1328.
- Building Code Requirements for Structural Concrete and Commentary: ACI 318 -05, ACI 318R -05. Farmington Hills. USA. 2005. 430 p.
- Eurocode 2. Design of Concrete Structures. Part 1. General Rules and Rules for Buildings: EN 1992 -1:2001. Brussels. 2002. 230 p.
- Vecchio, F.J. The Modified Compression Field Theory for Reinforced Concrete Elements Subjected to Shear/F.J. Vecchio, M.P. Collins//ACI Journal, Proceedings. 1986. Vol. 83, № 2. P. 219-231.
- Филатов, В.Б. Расчетная модель наклонного сечения железобетонной балки с учетом сил зацепления в наклонной трещине/В.Б. Филатов, Е.В. Блинкова//Промышленное и гражданское строительство. 2014. № 3. С. 39-42.


