Анализ распределений и взаимосвязи индексов племенной ценности симментальских быков-производителей австрийского происхождения при использовании геномной селекции

Автор: Мурленков Н.В., Шендаков А.И.

Журнал: Биология в сельском хозяйстве @biology-in-agriculture

Рубрика: Актуальные вопросы зоотехнии и ветеринарии

Статья в выпуске: 4 (41), 2023 года.

Бесплатный доступ

Популярность программы геномной оценки быков в странах ближнего зарубежья за последние несколько лет привела к развитию методов молекулярно-генетического маркирования, а возникшая возможность геномного сканирования, позволила одновременно анализировать тысячи локусов в одном геноме. Такие методы геномного сканирования позволяют проводить картирование главных генов, ответственных за хозяйственно ценные признаки, на основе полиморфизма генетических маркеров. Благодаря геномной селекции, использующей различные индексы, степень выявления ценности животных возрастает уже в раннем возрасте, что определяет новизну и актуальность в системе племенной работы. В представленной статье изучены закономерности взаимосвязи и сила влияния ведущих племенных индексов при геномной оценке производителей. Объектом представленного исследования служили симментальские быки-производители разных возрастов, предметом - племенные индексы, характеризующие продуктивные и физиологические особенности животных. Анализ первичных данных по каждому быку проводился на базе «IBM SPSS Statistics» 27 с применением параметрических и непараметрических критериев. Была определена нормальность распределения изучаемых индексов (нулевая гипотеза сохраняется); выявлены достоверные различия между группами животных в зависимости от возраста (от 6,22 до 60,43, при p=0,01); проведен дисперсионный анализ при влиянии возраста на величины индексов (GZW - 2195,1; MW и FIT - 683,4 и 597,9, при р=0,0005); изучена степень взаимосвязи индексов методом парных корреляций (GZW и MW: +0,739; GZW и FIT: +0,628, при р=0,0005); построена регрессионная модель, которая описывает 61% случаев, где увеличение возраста быков влечет за собой возрастание индексов.

Еще

Племенные индексы, геномный анализ, быки-производители, корреляция, дисперсионный анализ, критерий достоверности, коэффициенты регрессии

Короткий адрес: https://sciup.org/147242260

IDR: 147242260

Текст научной статьи Анализ распределений и взаимосвязи индексов племенной ценности симментальских быков-производителей австрийского происхождения при использовании геномной селекции

него и дальнего зарубежья широкое распространение получил метод геномной оценки племенной ценности (далее GEBV). Геномная оценка в системе селекционно-племенной работы основана на анализе последовательностей ДНК животного [6]. GEBV рассчитывается для каждого хозяйственно-полезного признака с использованием индексов или молекулярногенетических меток, например, SNP-маркеров (однонуклеотидный полиморфизм) для определения племенной ценности животных.

В скандинавских странах Джозефом Мизенбер-гером (J. Miesenberger) на основе исследований австрийских симменталов был предложен новый ком- плексный индекс племенной ценности (GZW), объединяющий молочные, мясные и физиологические качества животных [8]. В этой связи представляется актуальным изучение современных аспектов геномной оценки быков-производителей и влияния основных индексов на формирование показателя общей племенной ценности (GZW). Представленные данные могут быть использованы в качестве научнометодического материала, а также служить основой для разработки селекционной базы, необходимой в племенной работе России.

Материалы и методы исследований. Исследования были проведены с использованием информации по документам первичного учета селекционных и геномных индексов, представленным на площадке Zuchtwert Austria. Был выполнен статистический анализ распределений и взаимосвязей племенной ценности быков-производителей симментальской породы в зависимости от возраста. Схема исследований, изучаемые индексы и применяемые методы математического анализа представлены в таблице 1.

Таблица 1 – Схема исследований

Быки-производители симментальской породы (n=3030)
Контрольная группа			1 опытная			2 опытная
Рожденные с 2020-2022 гг.			Рожденные с 2017-2019 гг.			Рожденные с 2014-2016 гг.
Изучаемые индексы
GZW		MW			FW			FIT
Общая племенная ценность		Молочная продуктивность дочерей			Откормочные качества			Фитнесс*
Статистические методы исследований
N d	t-test			d/g	ANOVA		r		R/R 2
Нормальность распределения	Распределение Стьюдента			Размеры эффектов	Дисперсионный анализ		Корреляция		Регрессия

Примечание: Фитнесс – индекс, включающий совокупность селекционных и физиологических признаков животных

Анализ первичных данных по каждому быку проводился на базе «IBM SPSS Statistics» 27 с применением параметрических и непараметрических критериев. Оценка нормальности распределения выборочной совокупности проводилась с использованием визуализированного метода (при помощи коробчатых диаграмм – «тьюков»). Проверка равенства средних осуществлялась с использованием критерия Стьюдента; для измерения силы взаимосвязи между переменными использовался метод сравнения эффектов, с применением критериев Коэна и Хеджеса; для оценки влияния факторов использовался дисперсионный анализ – ANOVA; оценка взаимосвязи проводилась с применением парных корреляций по Пирсону; по- строение регрессии осуществлялось линейным методом с определением зависимости по P-P графику.

Результаты исследований и их обсуждение. Перед использованием математических методов моделирования для определения статистической значимости и взаимосвязей между совокупностью данных, требуется соблюсти основное правило – проверить нормальность распределения изучаемых выборок. Данные рисунков 1-4 наглядно демонстрируют, что медианы всех четырех индексов расположены практически посередине коробчатых диаграмм. Таким образом, выборки подчиняются нормальному закону распределения, и параметрические тесты могут быть применимы.

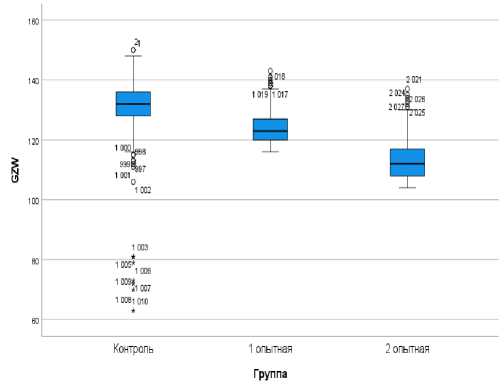
Рис. 1 – Нормальность распредления по индексу GZW

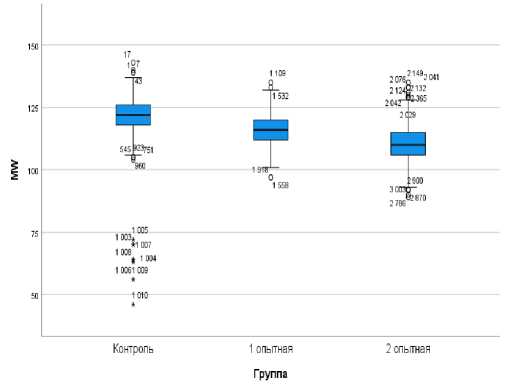
Рис. 2 – Нормальность распредления по индексу MW

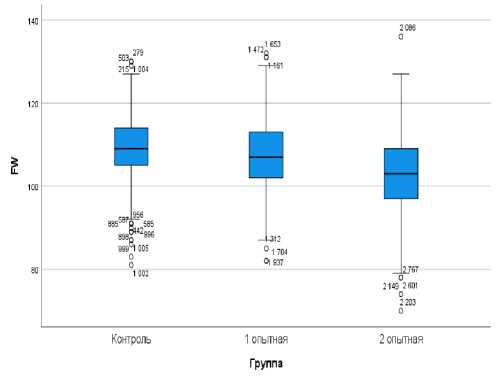
Рис. 3 – Нормальность распредления по индексу FW

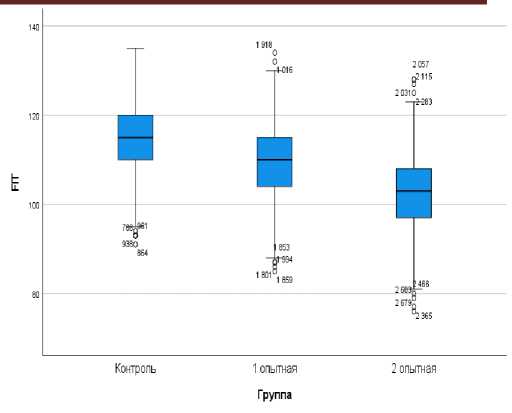
Рис. 4 – Нормальность распредления по индексу FIT

В таблице 2 была представлена проверка гипотез, основанных на распределении Стьюдента. Уро- вень значимости для оценки различий средних величин составил 0,05.

Таблица 2 - T -критерий для равенства средних

Показатели	T st	р	Средняя разность	MSE	95% ДИ
Показатели	T st	р	Средняя разность	MSE	Нижняя	Верхняя
Между контролем и 1 группой
GZW	27,403	0,01	8,211	0,300	7,623	8,799
MW	17,723	0,01	5,511	0,311	4,901	6,121
FW	6,228	0,01	2,145	0,344	1,469	2,820
FIT	15,479	0,01	5,421	0,350	4,734	6,108
Между контролем и 2 группой
GZW	60,432	0,01	18,965	0,314	18,350	19,581
MW	34,680	0,01	11,275	0,325	10,638	11,913
FW	16,561	0,01	6,168	0,372	5,438	6,898
FIT	34,624	0,01	12,287	0,355	11,591	12,983

Примечание : T st – критерий Стьюдента; р – двухсторонняя значимость; MSE - среднеквадратичная ошибка разности; ДИ – доверительный интервал

Т-тест Стьюдента при парном сравнении контрольной и опытных групп предполагал равные дисперсии и демонстрировал достоверные различия у всех племенных индексов (от 6,22 до 60,43) на уровне 0,01. Исследования также показали, что ДИ не вклю- чал нуль, поэтому с 95% вероятностью принимается альтернативная гипотеза о статистической значимости селекционных индексов на уровне не хуже 0,05.

Таблица 3 - Размеры эффектов парных выборок

Показатели			Стандартизатор	Точечная оценка	95% доверительный интервал
Показатели			Стандартизатор	Точечная оценка	Нижняя	Верхняя
Пара 1	Возраст - GZW	d Коэна	10,735	-11,236	-11,521	-10,951
Пара 1	Возраст - GZW	g Хеджеса	10,736	-11,235	-11,520	-10,949
Пара 2	Возраст - MW	d Коэна	8,737	-13,052	-13,382	-12,721
Пара 2	Возраст - MW	g Хеджеса	8,738	-13,050	-13,381	-12,719
Пара 3	Возраст - FW	d Коэна	8,866	-11,798	-12,097	-11,498
Пара 3	Возраст - FW	g Хеджеса	8,867	-11,796	-12,096	-11,497
Пара 4	Возраст - FIT	d Коэна	9,907	-10,799	-11,073	-10,524
Пара 4	Возраст - FIT	g Хеджеса	9,908	-10,797	-11,071	-10,523

Если p-значение может показывать статистически значимую разницу между двумя выборками, то размер эффекта (d Коэна, g Хеджеса) отражает величину полученной разницы. Показатель g Хеджеса яв- ляется более точной версией d Коэна, использующий поправочный коэффициент, а именно n - 1 для каждой выборки вместо n, что дает лучшую оценку. Эмпирические значения d и g в таблице 3 указывают на то, что средние парных групп отличаются на 8,866 – 10,736 стандартных отклонений. Согласно эмпириче- скому правилу парных эффектов, полученные данные имеют достаточно большой размах.

Таблица 4 – Однофакторный дисперсионный анализ (ANOVA)

Показатели		Сумма квадратов	ст.св.	Средний квадрат	F	знач.
GZW	Между группами	182729,676	2	91364,838	2195,116	0,0005
	Внутри групп	125989,395	3027	41,622
	Всего	308719,071	3029
MW	Между группами	64212,074	2	32106,037	683,484	0,0005
	Внутри групп	142190,652	3027	46,974
	Всего	206402,726	3029
FW	Между группами	19725,482	2	9862,741	146,438	0,0005
	Внутри групп	203400,159	3020	67,351
	Всего	223125,641	3022
FIT	Между группами	76593,383	2	38296,691	597,973	0,0005
	Внутри групп	193861,582	3027	64,044
	Всего	270454,965	3029

Проведенный однофакторный дисперсионный анализ в таблице 4 демонстрирует, что вне зависимости от возраста критерий Фишера (F) имел достоверные различия на уровне не хуже 0,0005. В тоже время наибольшие статически значимые различия были вы- явлены по индексу GZW – 2195,1, несколько слабее – по MW и FIT – 683,4 и 597,9 соответственно. Таким образом, проведенный анализ позволяет отвергнуть нулевую гипотезу и сделать вывод, что не все средние группы равны.

Таблица 5 – Корреляции парных выборок

Показатели		GZW	MW	FW	FIT
GZW	Корреляция Пирсона	1	0,739^**	0,385^**	0,628^**
	знач. (двухсторонняя)	-	0,0005	0,0005	0,0005
	N	3030	3030	3023	3030
MW	Корреляция Пирсона	0,739^**	1	0,124^**	0,045^*
	знач. (двухсторонняя)	0,0005	-	0,0005	0,014
	N	3030	3030	3023	3030
FW	Корреляция Пирсона	0,385^**	0,124^**	1	0,032
	знач. (двухсторонняя)	0,0005	0,000	-	0,080
	N	3023	3023	3023	3023
FIT	Корреляция Пирсона	0,628^**	0,045^*	0,032	1
	знач. (двухсторонняя)	0,0005	0,014	0,080	-
	N	3030	3030	3023	3030

Примечание : * – корреляция значима на уровне 0,05; **

– корреляция значима на уровне 0,01

Согласно данным таблицы 5, наибольшие положительные корреляции наблюдались по: GZW и MW – 0,739; GZW и FIT – 0,628 при двусторонней значимости 0,0005 (p<0,01). Умеренная связь прослеживалась между: GZW и FW – 0,385; MW и FW – 0,124 при двусторонней значимости 0,0005 (p<0,01). Таким образом, при увеличении индексов молочной продуктивности и фитнесса общая пленная ценность также будет увеличиваться и наоборот.

Для изучения влияния племенных индексов на возраст быков-производителей был проведен линейный регрессионный анализ – «модель 1» (табл. 6), где предикторами выступали GZW, MW, FW и FIT, а константой служил возраст животных. Значение коэффициента детерминации (R) составило 0,784, что говорит о достаточно тесной взаимосвязи между племенными индексами и возрастом быков-производителей. Величина R-квадрата составила

0,614, а значит, приведенная модель описывает 61% случаев, при которых увеличение значений индексов происходит за счет увлечение возраста быков.

Таблица 6 – Сводка для модели регрессии 1

О s

Й ч cd PQ ¥ pi

св Н СО g о а

a pi

и и

° S те

0,784

0,614

0,507

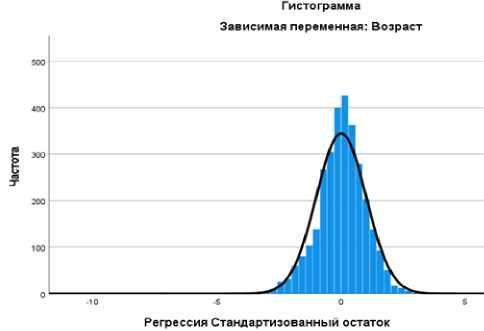
Рис. 5 – Гистограмма регрессионного распределения

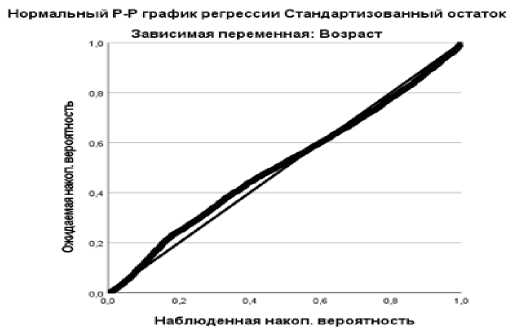
Рис. 6 – Нормальный P-P график регрессии

В линейной регрессии предполагается, что разница предсказанных и наблюдаемых значений распределены нормально. Однако прежде чем сделать вывод, необходимо рассмотреть гистограмму (рис. 5) и вероятностный график (P-P) остатков для визуального анализа (рис. 6). Анализ рисунков показывает, что между значениями племенных индексов и возрастом быков существует нормальная положительная зависимость. Соответственно, если величина индекса увеличивается, то возраст животных возрастает линейно.

Таблица 7 – Коэффициенты регрессии модели 1

Модель		Нестандартизованные коэффициенты		т	р
Модель		B	Стандартная ошибка	т	р
1	(Возраст)	16,766	0,525	31,918	0,0005
	GZW	0,027	0,006	4,192	0,0005
	MW	-0,072	0,005	-13,462	0,0005
	FW	-0,029	0,002	-12,320	0,0005
	FIT	-0,060	0,004	-14,611	0,0005

При выполнении линейной регрессии, полученные значения нестандартизированы, то есть используются необработанные данные для поиска линии наилучшего соответствия (табл. 7). Нестандартизиро-ванный коэффициент B по константе (возрасту) сообщает среднее значение переменной отклика (19,76), в том случае если предикторы принимают нуль. Коэффициенты B по GZW, MW, FW и FIT говорят об изменении значения отклика, связанном с увеличением на единицу переменной предиктора. Таким образом, увеличение GZW на одно стандартное отклонение связано с увеличением возраста быков на 0,027 стандартного отклонения, при условии, что остальные индексы остаются неизменными. Соответственно, увеличение MW, FW и FIT связано с уменьшением возраста быков на 0,072, 0,029 и 0,060, если предположить, что значение GZW постоянно.

Заключение. На основании представленных исследований были сформированы следующие выводы:

1. Коэффициент Стьюдента для контрольной и опытных групп демонстрировал достоверные различия у всех племенных индексов (от 6,22 до 60,43) на уровне 0,01. Кроме того, наибольшие различия прослеживались у контрольной и 2 опытной группы – в пользу молодых животных.
2. Эмпирические значения Коэна и Хеджеса указывало на то, что средние парных групп отличались
3. Корреляционная матрица индексов показывала наибольшую положительную связь между GZW и MW: +0,739; GZW и FIT: +0,628 при значимости 0,0005 (p<0,01). Соответственно, это доказывает, что на формирование общей племенной ценности в основном влияли молочная продуктивность и фитнесс, что закономерно.
4. Дисперсионный анализ демонстрировал, что наибольшие статически значимые различия между возрастом и индексами были выявлены по GZW – 2195,1, MW и FIT – 683,4 и 597,9 при значимости 0,0005. Отсюда можно сделать вывод, что племенная работа в большей степени ведется по молочной продуктивности и состоянию здоровья животных, нежели по мясным качествам.
5. Регрессионная модель описывала 61% случаев, при которых увеличение значений индексов происходило за счет увлечения возраста быков. Также увеличение GZW на одно стандартное отклонение связано с увеличением возраста быков на 0,027 стандартного отклонения; увеличение MW, FW и FIT, наоборот, – с уменьшением возраста быков на 0,072, 0,029 и 0,060, соответственно.

на 8,866-10,736 стандартных отклонений. При этом, у более молодых особей размер эффекта по GZW был выше, а значит, разница между средним животным в каждой группе также была больше.

Список литературы Анализ распределений и взаимосвязи индексов племенной ценности симментальских быков-производителей австрийского происхождения при использовании геномной селекции

Геномные технологии в молочном животноводстве // URL: https://igene-ferma.com/wp-content/uploads/2018/05/gebv_smsz.pdf (дата обращения 09.09.2023 г.).
Зубенко Э.В., Некрасов Д.К. Использование метода селекционных индексов для прогнозирования племенной ценности быков черно-пестрой породы по пожизненному удою дочерей // Вестник АПК Верхневолжья. 2012. № 4 (20). С. 28-32. EDN: PXZBKP
Карымсаков Т.Н., Абугалиев С.К., Баймуканов Д.А. Оценка племенной ценности быков-производителей по геномному анализу // Аграрная наука. 2019. № 10. С. 40-42. EDN: NCXVPC
Кругляк О.В. Хозяйственно-экономические предпосылки внедрения геномной оценки животных в молочном скотоводстве // Международный научно-производственный журнал "Экономика АПК". 2013. № 9 (227). С. 085-091. EDN: RDHHPP
Попов Н., Некрасов А., Федотова Е. Генетическое маркирование в селекции скота // Животноводство России. 2020. № S2. С. 9-15. EDN: ZXFJUR
Смирнов Е.А. Геномная оценка быков и её использование в молочном скотоводстве // Modern research and technology - 2023: сборник статей Международной научно-практической конференции. Петрозаводск, 2023. С. 220-224. EDN: NWBVBS
Шаркаева Г.А Анализ племенной ценности быков по геномной оценке и качеству потомства // Проблемы и перспективы повышения эффективности племенного животноводства и кормопроизводства: материалы международной научно-практической конференции. Тверь, 2021. С. 137-139. EDN: KPYXZR
Miesenberger J., Fuerst Ch. Experiences in selecting on a total merit index in the Austrian Fleckvieh breed // Biotechnology in Animal Husbandry. 2006. Vol.22, pp 17-27.

Еще

Статья научная