Анализ развития пластической деформации в поверхностном слое при ультразвуковом алмазном выглаживании

Величина пластической деформации в поверхностном слое при алмазном выглаживании (АВ) обусловлена приложенной к материалу определенной статической нагрузки. Вместе с тем, согласно эффекта Блага-Лангенеккера [1] при энергетическом воздействии ультразвуковых колебаний возможно снижение предела текучести материала, он становится более пластичным, что обусловлено увеличением плотности подвижных дислокаций в поверхностном слое (ПС). Под действием напряжений движение и размножение дислокаций осуществляется в определенных плоскостях скольжения, различным образом ориентированных в зернах. Действующие плоскости скольжения наблюдаются как система линий скольжения, состоящих из множества выхода дислокационных линий. Развитие пластической деформации во времени происходит в результате увеличения плотности полос скольжения, их расширения, за счет механизма двойного поперечного скольжения (ДПС) и последующего слияния.

Установив закономерности кинетики накопления плотности дислокаций в деформируемом объеме ПС от условий внешнего воздействия при ультразвуковом алмазном выглаживании (УЗАВ), представляется возможным воздействовать на характер протекания пластической деформации в ПС, а следовательно, и управлять его прочностными свойствами и обеспечивать на выходе требуемые параметры качества.

Целью настоящего исследования являлось установление количественной взаимосвязи накапливаемой плотности дислокаций в деформируемом объеме ПС с внешними параметрами процессов АВ и УЗАВ.

РЕЗУЛЬТАТЫ

7 ⁽z ) = ⁷ 0,2 + ^а‘ G • b • V Р ⁽z ) , (1) где ^ i ( z ) - интенсивность напряжений, Н/мм², действующих на некоторой глубине z , от поверхности мм; а 0 2 — условный предел текучести; а — коэффициент междислокационного взаимодействия (0,1…0,2 [3]); G – модуль сдвига, Н/ мм²; b - вектор Бюргерса, мм; р (z ) - плотность дислокаций на глубине z , 1/мм²

Из (1) можно получить формулу для расчета плотности дислокаций, в зависимости от действующих напряжений:

Р ^{( z} )

⁷ i⁽ z ) — ⁷ 0,2

K

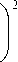
где K = а • G • b .

Для расчета плотности дислокаций на глубине z по формуле (2) необходимо знать величину напряжений а ■ ( z ) , действующих на этой глубине.

Для этого следует установить характер их распределения по глубине поверхностного слоя в результате действия внешней нагрузки. Из приближенного решения упруго-пластической задачи о напряженном состоянии в полубесконечном теле при внедрении шара воспользуемся выражением для расчета интенсивности напряжений, полученное Б.А.Кравченко [4]:

7 ^{( z} ) = ⁷ о •

1,5

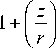
(1 + А ) - I (1

z       ( r М

---arctg I I I r       V z ))

, (3)

где 7 ₀ - нормальное давление на поверхности контакта инструмента с обрабатываемой поверхностью Н/мм²; Ц - коэффициент Пуассона ( Ц = 0,3 ); r – радиус отпечатка, мм.

Известно и другое выражение для расчета действующих напряжений в поверхностном слое, предложенное Я.И. Барацем [5]:

⁷ , ( z ) = а 0 •

2 •

r

² ' ( z/r ^{) 3}

4 ^{1 + (} zlr ) 2

Графические зависимости, построенные по формулам (3), (4) в безразмерном виде

" i /a , = f Vr ) •

показаны на рис. 1.

Как следует из анализа рис. 1 зависимости напряжений по глубине поверхностного слоя близки к показательному (экспоненциальному) распределению. Для аппроксимации графических зависимостей определим физически обоснованную область существования безразмерной координаты

z r . Полагаем, что напряжения изменяются от максимальных напряжений на поверхности контакта ( z = 0 ) до напряжений, действующих на некоторой глубине упрочненного слоя z = А . На глубине А интенсивность напряжений a i = a 02 ,где a 02 — предел текучести. На основании анализа работ в области обработки ППД отношение глубины упрочнен- ного слоя к радиусу отпечатка Ау , характерное для большинства процессов обработки ППД не превышает 3 [5, 6].

Автор [8] установил, что при контакте сферы с пластическим полупространством впервые пластические деформации возникают на глубине z * 0,5 • r .

Аппроксимируя графические зависимости, представленные на рис. 1. в физически обоснованном интервале значений безразмерной координаты zr , изменяющейся от 0,5 до

- / _ Л / _ а        ______________ zr = Ц = 3 , получим уравнение:

z ai(z) = a0 • exP( -0,8 • -) .       (5)

где a ^ - амплитуда напряжения, Н/мм², Г узк -радиус отпечатка при ультразвуковом воздействии инструмента, мм.

Для упрощения расчетов в случае ультразвуковой обработки, учтем только действие максимальных напряжений в поверхностном слое, возникающих в результате максимального дополнительного внедрения инструмента в поверхность на величину h д = 12 • 5 , где 5 - амплитуда колебаний, мкм.

Радиус отпечатка при ультразвуковой обработке r _УЗК определим из приближенного соотношения, устанавливающего связь радиуса отпечатка с глубиной внедрения инструмента в случае пластического контакта:

r = 2 • R u • h .               (7)

Для случая ультразвуковой обработки выражение (7) запишем в виде:

Г узк = V 2 • R • ( h + >2 • 5 ) .       (8)

Выполняя некоторые преобразования и учитывая (7) получим:

^ГУЗК ^r N^lxr ^,

где К = 1 +—-— - безразмерный коэффициент r 2 • h учитывающий увеличение радиуса отпечатка при ультразвуковой обработке.

Подставляя (5), (6) в (2), а также учитывая (9) и выполняя некоторые преобразования, получим для процесса АВ:

Р< z ) =

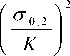
- 2

p^- • exp( - 0,8 • z ) - 1 , (10)

a 0,2                 r _ для процесса УЗАВ:

Для расчета интенсивности напряжений в случае наложения на инструмент УЗК и, учитывая дополнительное внедрение инструмента в обрабатываемый материал в результате действия амплитудного напряжения, получим решение:

•

( a + ap )            z

• ^exP^{( - 0},⁸ • 7F ) ^{- 1} . (11)

^U 0,2                  ^r K r _

^a i ( УЗК ) ^{( z} ) = ^{( a} 0 + ^a 5 ) • ^exP^{( - 0,8}--) , (6)

r УЗК

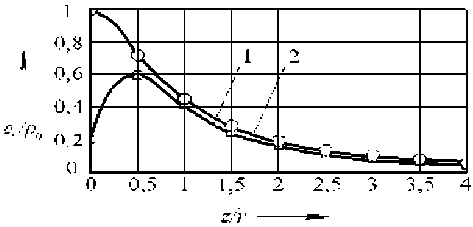
Рис. 1. Зависимости распределения безразмерного напряжения ^a у  по безразмерной координате у :

^a 0                             r

1 – зависимость по [5]; 2 – зависимость по [4]

Полученные уравнения характеризуют распределение плотности дислокаций в единице объема по глубине поверхностного слоя в зависимости от распределения в нем действующих напряжений. Однако, они не учитывают накопление плотности дислокаций за конечное время действия нагрузки на единичный микрообъем поверхностного слоя. Для расчета кинетики накопления плотности дислокаций в единице микрообъема поверхностного слоя рассмотрим скорость изменения плотности дислокаций по глубине. Расчет выполним для обычного АВ. Продифференцируем выражение (10) по dz :

d p dz

- 2 •

f ^a 0,2

\2

^{f a} 0 ) 0,8

I K J

I ^a 0,2 J   ^r

^ ^ )• exp( - 0,8 • z ) - 1

I ^a 0,2 J              ^r

z

• exp( - 0,8 • ) •x r

Уравнение (12) определяет скорость изменения плотности дислокаций по глубине z . Знак “минус” в выражении (12) показывает, что с увеличением глубины ПС скорость уменьшается.

За некоторый, бесконечно малый промежуток времени dt , дислокации, двигаясь со скоростью V g под действием напряжений, переместятся на расстояние dz . Очевидно, что за конечное время обработки t они распространятся наглубину z = Л (глубина упрочненного слоя). Таким образом, подставляя в (12) вместо dz выражение V g - dt , получим уравнение, характеризующее скорость изменения плотности дислокаций в деформируемом микрообъеме поверхностного слоя на глубине z в зависимости от времени dt действия нагрузки (знак “минус” опускаем):

t = —к- • N , где N - число циклов приложения V

нагрузки:

2 ( р—) = 3,2• k-I-----I- --l^2 I -I 0 |-exp(-0,8- -)•

I r J b ( K J ( — 0,2 J          r

° P I- exp( - 0,8 - z ) - 1 0 2 J r

⁺ р Их .

Принимая выражения для относительной

деформации e = hh^

2 • r

N =--- , учитывая K

s

d р о

= 2 • V dt ^д

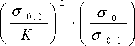
0,8      ,

--exP(

r

х I - ° - I • exp( - 0,8 • — ) - 1

А ^— 0,2 J               r

- 0,8 • ^— ) х

r

. (13)

В (15) неизвестна скорость дислокаций V g . Принимая во внимание, что скорость дислокаций связана со скоростью пластической деформацией соотношением V g = £ / b • р [2] ( e -скорость пластической деформации, и учитывая связь скорости £ со скоростью деформирования (выглаживания) V в виде £ = 8 Ду)L _K ) [6], получим формулу для расчета средней скорости движения дислокаций в микрообъеме ПС:

^V g

8 • V

L к • р • b

где ε – относительная деформация, определяемая для обработки выглаживанием из соотношения h_вн R_и ; h_вн – глубина внедрения инструмента в обрабатываемый материал, мм; L_к – длина контакта инструмента с обрабатываемой поверхностью, мм.

Подставляя (14) в (13) и, вводя некоторые обозначения, получим следующее выражение для скорости накопления плотности дислокаций в единичном микрообъеме ПС:

dP = А • 1

dt р ’

где А = 2 • L • ^и ° «Ч b L k I K J

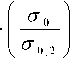
• 08 х

r

х exp( - 0,8 • ^— ) • r

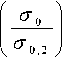
• exp( - 0,8 • ^— ) - 1 r

Выполняя интегрирование с учетом начальных условий t = 0 и р ( t = o ) = р исх , получим формулу для расчета плотности дислокаций в микрообъеме поверхностного слоя на глубине z за время обработки (время воздействия инструментом на единицу площадки контакта)

r ²

и числа циклов

2 • R и

= a - b - G , получим:

р - ) =

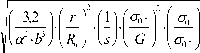
• exp - 0,8 • z ) •

° 2 l- exp - 0,8 - z ) - 1 .^— J r

⁺ f uc .

Для расчета контактного напряжения — ₀ воспользуемся соотношением, полученным в [6]:

'

^— 0 = c • ^— 0,₂

где коэффициент c = 2,87 •

I -HVz- X

V HV ( z ) J

, HV 0

и

HV ( z ) - соответственно значения исходной (после предшествующей обработки) микротвердости на поверхности и в глубине ПС.

С учетом (20), выражение (19) примет вид:

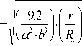
- ^{f 1} V ^— '^X - ^f Н^{0 X} - exp - °S - z ) -Г 2,87- Г Н^{0 X} - exp - °,S - z ) - 1 1+ A 2

I. s JI G J I H K z ) J uc. ^№ r     I HV,z ) J исх ^№ r’ J ^P”

Из (21), приравняв z = 0 , определим поверхностную плотность дислокаций:

1 1 9,2 If r X² f 1 If ^— 0,2 X² f НУ, X L,,, f нур   '

,*-J

Ж a ² • b ж I r J (s j I G J ( HV ( z )1         I HV ( z )1

и                                  Zixx L                   'сх^

^{+ рр} сх .

Для процессов механической обработки, предшествующих выглаживанию (точение, шли-

фование), отношение f ^HV ° 1 примерно равно I ^HV ( z ) J исх

1 [6]. Анализ зависимости (20) показал, что последний член слагаемого в правой части выражения не оказывает существенного влияния на величину р ₀ , поэтому представим итоговую формулу в виде:

рп =

4,15 X • ,a - b ^3/2 J

( А 1/2

r И 1 X

V ^{J v}u J V ^s У

f — 02 X .

V G J

С учетом (21) формула(19) примет следующий вид:

^{р z} ) =

I                                                      7. 7

0,53 - ( р 2 - р исх ) - exp( - 0,8 - -) • 2,87 - exp( - 0,8 - -) - 1 + р^.

r

r

Упростим выражение (24), разложив экспо-нециальные члены в ряд и ограничившись первыми двумя членами ряда, а также учитывая, что ( р 0 /р „сх ) ² >>1,^{в итоге по}луч^им:

Р ⁽z ) = Р о J ¹ - ^0,8 • z I . V r J

разований, а также учитывая

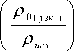
>>1, фор-

Аналогичным образом получим расчетные соотношения для определения плотности дислокаций, накапливаемых в единице микрообъема ПС при УЗАВ.

С учетом числа циклов приложения нагрузки

мула (25) примет следующий вид:

P ( z ) ( узк ) = Р 0(УЗК )J ^eXP^{( - 0,8} r ^TKy ) •

f 2,87 • K_p J

V ^2,87 • K p - 1 ^J

• exp( - 0,8— r ^

zT= ) - 1

K r

при ультразвуковой обработке N =

60 - f s • V

^П ' (уузк )

получим следующее выражение:

^Р z ) ( узк ) =

А - exp - 0,8 4= ) • r J K r

I- exp - 0,8-4=) - 1

° 0,2    J r • V K

+ p_cx исх ,

где

А =

0,3 ^f r ^{3 1} f Л ^f ° 0 ⁺ ° — If ° 0,2 I

•                 -- K •                             • I I

( a ² • b ³) V R И J s • V ^r V ° ₀,₂ J V G J

Принимая z = 0 в выражении (24) и учитывая принятое обозначение А , получим формулу для расчета поверхностной плотности дислокаций при ультразвуковой обработке:

Таким образом, получены аналитические зависимости для расчета плотности дислокаций накапливаемых в единице деформируемого микрообъема ПС в зависимости от параметров процессов АВ и УЗАВ

Используя полученные уравнения для конкретных условий обработки АВ и УЗАВ, можно составить критериальные уравнения, обеспечивающие взаимосвязь деформационных процессов, происходящих в поверхностном слое с внешними, управляемыми параметрами обработки.

Работа выполнена при поддержке Федерального агентства по образованию рамках ФЦП “Научные и научно-педагогические кадры России на 2009 – 2013 года” по направлению “Создание и обработка кристаллических материалов” (мероприятие 1.2.2, госконтракт № П990).

Р =    03 . f у_ J - f • K 32 • ^f °Л° — J-f ° , J ² ГГ °+° — J- f

^{0( узк} )      ( a ² • b ²) V R 2 J s - V    r V   ° 0,2   ^J V G J LI   ° 0,2   J _

⁺ py

Введем безразмерный коэффициент

° 0 ⁺ ° #

К _p =----- — , характеризующий отношение

° 0

контактного давления при АВ иУЗАВ. С учетом коэффициента К_p , а также выражения (19), учитывая принятые допущения, формула (25) преобразуется к виду:

• [ 2,87 • K - 1 ] + p 2„ p исх .