Анализ речевого сигнала с помощью процедуры реконструкции математической модели речевого процесса по порождаемому речевому сигналу

Технология обратной фильтрации является в настоящее время наиболее популярной для анализа речевого сигнала при оценке эмоционального состояния диктора, распознавании его пола, идентификации и имеет большое значение для ограниченного доступа к информации в комплексных системах защиты информации.

При исследовании речевого процесса используется модель речевого тракта [1] и модель голосового источника [2]. Анализ речевого сигнала предполагает получение информации о параметрах модели голосового источника и форме речевого тракта. На практике используется аппроксимация передаточной функции речевого тракта. Для аппроксимации передаточной функции речевого тракта в настоящее время используется метод линейного предсказания [3].

Передаточную функцию A(z) можно предста вить в z-области как [4]

A ( z ) =----1------ ’

1 + 1 a z " i

где a _i определяются с помощью анализа речевого сигнала моделью линейного предсказания порядка p. Сигнал пропускается через фильтр с передаточной функцией 1 / A ( z ) . Проинтегрированный отклик этого фильтра служит оценкой объемной скорости воздушного потока через голосовую щель по речевому сигналу. Коэффициенты линейного предсказания содержат информацию о форме речевого тракта.

Основной проблемой данного подхода является неустойчивость модели линейного предсказания к типу микрофона и внешним шумам. Искажения проявляются в виде всплесков на графике производной объемной скорости и объемной скорости воздушного потока после обратной фильтрации, по амплитуде превосходящих пики исследуемых сигналов, что отрицательно сказывается на последующем вычислении площади голосового источника.

Задачей настоящего исследования является представление альтернативного подхода к анализу речевого сигнала с помощью процедуры реконструкции математической модели динамической системы по порождаемому временному ряду. В этом случае ai определяются с помощью анализа речевого сигнала реконструированной моделью речевого процесса по речевому сигналу. Такой подход более устойчив к внешним искажениям и существующие всплески не превышают максимума исследуемых сигналов.

Все представленные в данной работе вычисления проводились на материале синтезированных гласных звуков. Благодарю авторов работы [4] за предоставленные синтетические гласные, а также за обсуждение некоторых аспектов работы.

• 2.    Восстановление объемной скорости воздушного потока через голосовую щель с помощью процедуры реконструкции математической модели динамической системы по порождаемому временному ряду и известной модели

Восстановление объемной скорости воздушного потока предполагает следующий алгоритм.

Подвергнем предыскажению исследуемый речевой сигнал с помощью нерекурсивного фильтра первого порядка [4]

Q ( z ) = 1 - 0 , 9 z ^{- 1} . (2)

Определим длительность временного окна анализа равной 25 мс – это 200 отсчетов при частоте дискретизации 8 кГц. Определим сегмент, содержащий максимум по амплитуде, для дальнейших исследований. Такой подход позволяет избежать нестыковки анализируемых сегментов по амплитуде.

Применим к исследуемому сегменту речевого сигнала процедуру реконструкции математической модели речевого процесса по речевому сигналу. Реконструируемая модель имеет вид определяются с помощью линейного метода наименьших квадратов (МНК) [5].

Теперь пропустим исследуемый сегмент речевого сигнала через фильтр с передаточной функцией 1 /A ( z ) , где A ( z ) определяется с помощью (1). Вместо a i будем использовать c i . На выходе получим оценку производной объемной скорости воздушного потока через голосовую щель.

Воспользуемся представлением [2; 4]

aecxp0hw2 (t + At) - 2[w(t )(1-a) -w(t+At)] x x S (t + At) - 2aeAp(t + At)S2 (t + At) = 0,    (4)

-xt /Т n _ T    rp _ Poh Д t где a -1 - e , p - —- , T - -—, ^t - период Poh        kmp дискретизации по времени, S – площадь голосовой щели; w - линейная скорость потока; ктр -коэффициент вязкого трения; ρ0 – плотность воздуха; h – глубина голосовой щели вдоль оси потока; b – наименьший размер капиллярной трубки прямоугольного сечения; Δp – перепад давления над голосовой щелью; cx – коэффициент динамического сопротивления; μ – коэффициент вязкости воздуха. Представленные параметры определяются с помощью экспериментальных исследований и фиксируются в середине определенных диапазонов [2].

Решая (4) относительно объемной скорости w , получаем [2; 4]

1 + 4 aa -1 w< + At ) = ^       '2 ,

2a2

где        a1 = w(t) +a[pAp(t + At )S (t + At) - w(t)], n _ “PcxPo

² 2 S ( t + A t ) "

Площадь S ( t ) вычисляется с помощью [4]

tt  t

J Xdt = X _i ; J X _i dt = x ₂ ; J X ₂ dt = x ₃ ;

00  0

x = f (x 1 ,x ₂ ,x ₃ ) = c ₀ + C 1 X 1 + c ₂ x ₂ + c ₃ x ₃ +

+ C4 X1X2 + C5 X1X3 + С б X2 X3 + C7 X1X2 X3 +

22   2   2    2

+ С8Xi + С9X2 + СюX3 + C_nXi X2 + С12 Xi X3 +

max

⎛ sin⎜⎜

⎝

nt

⎤ ^α

⎟

^2t 1 T 0 у

0 < t < tiTo;

S max

cos⎜⎜ ⎝

^{β n ( t - t l T o} ) 2 ( t 2 - t i ) T o J]

, t i T o <  t <  t 2 T o ; ⁽⁶⁾

2  222

+ C13X1 X2 X3 + С14 X1X2 + С15 X1X2 X3 + С 16 X2 X3 +

0 ,

t2To < t < To,

2        2          2      22

+ С17X1X3 + С18X2X3 + С19XpX2X3 + С20Xi X2 +

22       22     2  2

+ C21X1 X2 X3 + С 22 Xi X3 + С23Xi X2X3 +

22     22    222

+ c24 ^X 2 ^X 3 ⁺ c25 ^X i ^X 2 ^X 3 ⁺ c26 ^X i ^X 2 ^X 3 ^.

Здесь x - речевой сигнал, зависящий от времени t; x1, x2, x3 - возбуждение в голосовой щели (входной процесс), co>•••>^26 - коэффициенты, содержащие информацию о форме речевого тракта, где t1 – отношение фазы открытия голосовой щели к T0, t2 - отношение интервала открытой голосовой щели к периоду T0, a, в - коэффициенты, определяющие скорость раскрытия и закрытия голосовой щели, Smax – максимальная площадь голосовой щели. Вычисленная объемная скорость нормируется до 200.

• 3.    Сопоставление оцененных с помощью процедуры реконструкции и модели линейного предсказания объемных скоростей воздушного потока через голосовую щель с вычисленной объемной скоростью

Сопоставление возможностей восстановления объемной скорости с помощью коэффициентов моделей линейного предсказания и модели реконструкции в алгоритме обратной фильтрации проводилось на материале синтетических гласных /а/, /и/, /у/. Каждая гласная была синтезирована для частоты основного тона 100 Гц. В таблице 1 представлены конфигурации голосовой щели для каждой из гласных.

Таблица 1. Конфигурации голосовой щели

Тип голоса	t 1	t 2
Придыхательный голос	0,46	0,77
Скрипучий голос	0,3	0,5

Сопоставление проводилось на одном (первом) периоде основного тона, то есть на временном окне малой длительности. Для сравнения использовалась величина абсолютной среднеквадратической погрешности. Результаты представлены в таблицах 2; 3.

Таблица 2. Абсолютная среднеквадратическая погрешность для линейного предсказания

гласные	/а/	/и/	/у/
придыхательный голос	0,0364	0,0239	0,1186
скрипучий голос	0,0550	0,0428	0,0482

Таблица 3. Абсолютная среднеквадратическая погрешность для процедуры реконструкции

гласные	/а/	/и/	/у/
придыхательный голос	0,0280	0,0583	0,0280
скрипучий голос	0,0430	0,0352	0,0291

На рис.1-2 представлены графики вычисленной и полученной после обратной фильтрации объемной скорости для модели линейного предсказания и процедуры реконструкции.

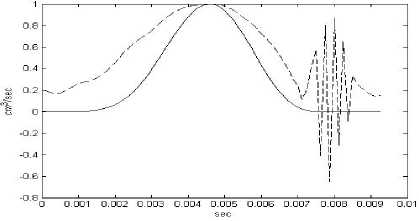
Рис.1. Сопоставление вычисленной и экспериментальной объемных скоростей для гласной /а/, с периодом основного тона – 0,01 для придыхательного типа голоса (сплошная линия – вычисленная объемная скорость, пунктирная линия – экспериментальная объемная скорость), модель линейного предсказания

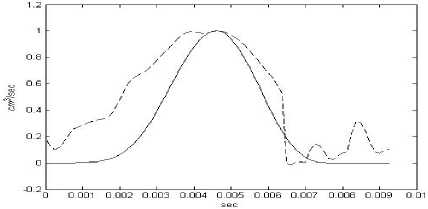
Рис.2. Сопоставление вычисленной и экспериментальной объемных скоростей для гласной /а/, с периодом основного тона – 0,01 для придыхательного типа голоса (сплошная линия – вычисленная объемная скорость, пунктирная линия – экспериментальная объемная скорость), процедура реконструкции

Таким образом, применение коэффициентов модели (3) при обратной фильтрации исследуемого речевого сигнала оправдано и способствует уменьшению зависимости обратной фильтрации от внешних воздействий.

• 4.    Заключение

В работе представлен анализ речевого сигнала с помощью процедуры реконструкции математической модели динамической системы по порождаемому временному ряду. Для анализа использовалась технология обратной фильтрации с помощью процедуры реконструкции и линейного предсказания.

Показано, что применение процедуры реконструкции может являться альтернативным подходом при обратной фильтрации речевого сигнала, и позволяет снизить результаты негативного внешнего воздействия. Таким образом, коэффициенты модели (3), содержащие информацию о форме речевого тракта, могут использоваться при решении практических задач.