Анализ резонансных явлений в выходной цепи двухтактного усилителя мощности класса D

С увеличением тактовой частоты и коммутативные потери должны расти. Однако при экспериментальном исследовании двухтактного усилителя был обнаружен отчетливо регистрируемый минимум потребляемой энергии в определенной области значений и. Это обстоятельство дало основание предположить, что в выходной цепи усилителя имеют место резонансные явления, учет которых позволит увеличить КПД усилителя. Для этого необходимо определить зависимость резонансных явлений от основных параметров схемы усилителя, а также от частоты и формы импульсов выходной тактовой последовательности.

Анализ схемы двухтактного усилителя класса D. Поскольку явление резонанса наиболее отчетливо проявляется в режиме молчания, то дальнейший анализ будет выполнен именно для этого режима.

Воспользуемся упрощенной схемой двухтактного усилителя (рис. 1, а ), в которой ключи S в идеализированной форме представляют активные элементы и обратные диоды, обеспечивающие непрерывность тока в дросселе L . Также предполагается, что в открытом состоянии внутренние сопротивления активных элементов и диодов равны и постоянны. Такая идеализация весьма условна, но может быть принята, поскольку она существенно не скажется на характере исследуемых процессов.

В режиме молчания усилителю соответствует эквивалентная схема (рис. 1, б), в которой нагрузочная цепь представлена входной индуктивностью фильтра нижних частот L , а электронные ключи заменены генератором импульсного сигнала u ( t ) со скважностью 2, внутренним сопротивлением R i и выходной емкостью С = 2 С ₀ .

б

а

Рис. 1. Упрощенная ( а ) и эквивалентная ( б ) схемы двухтактного усилителя класса D

Запишем для эквивалентной схемы следующие дифференциальные уравнения:

d²        1 d i u ( ^т )

4 +--- + ~т =             (1)

d т ² v ю ₀ CR i d т v ² R i v ²

d2     i i

—— -I = —1—.

2 2 n 2 , d т v Rv

где т = и t ; u (t) = E ... (п > т > 0); и (т) = - Е ...(п < т < 2п);

1        ю и = -v=; v = —.

V LC    Ю 0

На интервале 2 1 п < т < (2 1 + 1)п, ... ( 1 = 0, 1, 2, 3,...) решение (1) в установившемся в режиме имеет вид

i-R- = 1 -

E

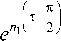
eⁿ n

f ") т- l 2J

4 n ) . Г л)I 1 —L I ch I n1 I

l n 2 J l 2J

^^^^^^»

4 n ) uf П) I 1 —2 I ch I n2 ~ I l n1 J l 2 J

где n i , n ₂ - корни характеристического уравнения (1).

На интервале (2 1 + 1)п < т < ( 1 + 1) 2п обозначим i = i ‘. Тогда согласно [2]

i ‘ = - i (т - п).

Ток i 1 определим в соответствии с (3):

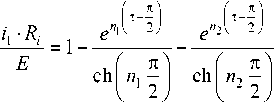
Аналогично (4) получим

i ‘ 1 = - i 1 (т - п).

Мощность потерь в ключевых элементах усилителя. Определим мощность потерь в ключевых т = ω0/ωс. Тогда выражение для корней характеристического уравнения примет вид элементах усилителя:

л

П

P =  f- 2 ■ Rd т + 2п J 1 -

2 л

J .;2^ т = 1J^ n R

Л

i

-1 ■ R)"

^J—- d т ,

E J

n 1,2 =

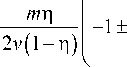
4 ( 1 -n ) 2 m 2 n 2

Подставляя значение i 1 из (5), получим

PR ,2 f 2

—т = ^1+_I-----

E ²      n ( n 1 + n ₂

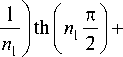
Полагая, как и в предыдущем случае, т >  2 и η→1,

+ —

П

ⁿ 1 ⁺ n 2

1 j    f     П j

- th n , n 2 J  I   2 J

получим

1 -n            m n n1 *--v,     n 2 *-         .

mn            v (1 -n)

Предположим, что фильтр нижних частот с частотой среза ω c согласован с нагрузкой и ω cL = R . Обозначим отношение ω/ω c через q и введем понятие электронного КПД усилителя:

R n =         .

R + R

При фиксированной частоте паразитного контура параметр v = ω √LC пропорционален тактовой частоте.

Анализ зависимости коммутативных потерь от тактовой частоты, построенной на основании (7) и (9), для частного случая т = 3 и η = 0,8 (рис. 2, б ) показы-

Тогда для корней характеристического уравнения

вает, что в этом случае возникают резонансные явления, причем минимум потерь (и потребляемой мощности) соответствует тактовой частоте, которая примерно в 1,5 раза превышает частоту паразитного ре-

n 1 , п 2 получим следующее выражение:

n =___ q n___ 1,2 2 v 2 ( 1 -n )	.- 1 ±^	2 4 v 2 ( 1 -n ) 1         2 2 q n 7

При q > 2 и η→1

1 -n qn ’

q ⁿ . V ² ( 1 -n )

зонанса.

Анализ потерь в усилителе при конечной длительности фронтов выходной импульсной последовательности. Как было установлено выше, при исследовании зависимости потерь от выходной емкости резонансные явления не были обнаружены. Вместе с тем очевидно, что при замене в схеме (см. рис. 1, б )

При неизменной тактовой частоте параметр v ² = ω² LC пропорционален емкости С .

В частном случае, когда q = 3 и η = 0,8, резонансные явления отсутствуют (см. график зависимости коммутативных потерь от выходной емкости на рис. 2, а , показанный пунктирной линией).

Рассмотрим зависимость коммутативных потерь от тактовой частоты ω. Для этого введем параметр

генератора меандра на генератор синусоидального сигнала резонанс должен иметь место. Следовательно, погрешность исходных предположений заключается в идеализации формы напряжения эквивалентно-

го генератора.

Для проверки этой гипотезы воспользуемся представлением и (τ) в виде гармонического ряда [2]:

, _x 4 E -^ sin ( 2 п- 1 ) т u ( т ) =

П n : 1     2 n - 1

.

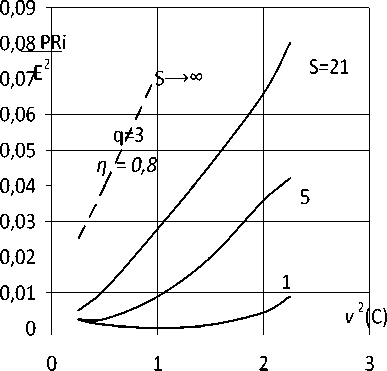
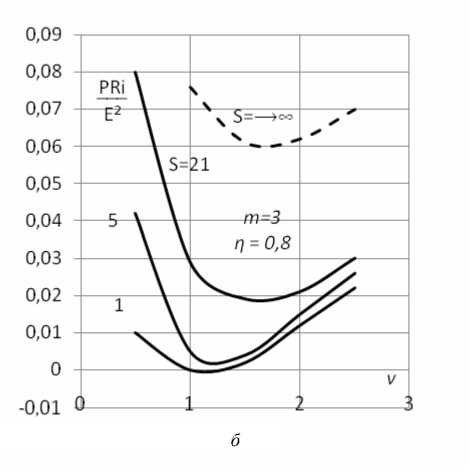
Рис. 2. Зависимость коммутативных потерь в усилителе от выходной емкости ( а ) и тактовой частоты ( б )

Удерживая в разложении (10) конечное число членов, определим потери в ключевых элементах. Для этого найдем модуль сопротивления нагрузочной цепи генератора для каждой гармоники и (τ):

x „      j to nLZ (n) = R +7,

^V ‘ 1 -to ² LCnn

откуда

n to L

I ^{Z (} n )l R^l J¹ n2 1

у Ri L1— n to LC _

Используя принятые ранее обозначения и (11), определим гармоники тока i 1 согласно (10):

– при изменении выходной емкости v ²

4 E

11 k = —i——т =--- kn |Z (k )|

Rikn,

4 E

2; (12а)

1 +

– при изменении частоты v

1 1 k =

4 E

Rik П

1+

kq n

,

"|2

km n v

)J

)_

(12б)

где k = 2 n – 1.

По аналогии с (7) мощность потерь можно определить следующим образом:

PR = f 1 1 2 1 k . RR, = 11 [ I 1 kR . 1 , (13)

E   ^7 1 2       ¹E    2 fl I E )

где S – номер высшей гармоники, удерживаемой в разложении (10) и связанный с длительностью фронта

импульсов выходного напряжения ∆ t. Для этого можно воспользоваться приближенной формулой

A t « 0,4 —.

to-S

Результаты расчета согласно (13) представлены на рис. 2.

Из анализа графика на рис. 2, а следует, что при конечной длительности фронта u ( t ) ( S < 5), резонансные явления возможны и при изменении выходной емкости усилителя.

Таким образом, можно сделать следующие выводы:

– при оптимальном выборе тактовой частоты в режиме молчания возможно существенное сокращение энергии, потребляемой усилителем;

– резонансные явления в выходной цепи усилителя класса D проявляются тем сильнее, чем больше длительность фронта импульсного напряжения. Однако необходимо иметь в виду, что затягивание фронта тактовых импульсов ведет к росту прямых потерь в режиме усиления сигналов;

– заметный эффект может быть получен, если увеличивать длительность фронта в паузах усиливаемого сигнала.